變頻激勵(lì)響應(yīng)分析及模態(tài)阻尼反演理論研究

唐宇航，王雪仁，李 欣,2

（1.中國人民解放軍92578部隊(duì)，北京100161；2.陸軍裝甲兵學(xué)院，北京10072）

0 引 言

潛艇的聲輻射與結(jié)構(gòu)材料的阻尼性能密切相關(guān)，阻尼參數(shù)作為一項(xiàng)重要的動(dòng)力性能指標(biāo)，對(duì)結(jié)構(gòu)在共振區(qū)的響應(yīng)影響十分顯著。目前，艦艇振聲性能設(shè)計(jì)計(jì)算時(shí)，其數(shù)值常按規(guī)范資料圖譜選取，規(guī)范資料的準(zhǔn)確性依賴統(tǒng)計(jì)規(guī)律保證，新船型是沒有進(jìn)入統(tǒng)計(jì)樣本的，對(duì)所有船型（尤其是新船型）籠統(tǒng)地采用相同經(jīng)驗(yàn)阻尼進(jìn)行振動(dòng)響應(yīng)預(yù)報(bào)及噪聲性能評(píng)估是不準(zhǔn)確的。因此，阻尼參數(shù)亦需要通過試驗(yàn)來測(cè)定，然而試驗(yàn)條件的微小差異也可能會(huì)造成測(cè)量結(jié)果的巨大偏差。雖然國內(nèi)外也制定了相關(guān)行業(yè)標(biāo)準(zhǔn)，但事實(shí)上并沒有在科研和生產(chǎn)上嚴(yán)格執(zhí)行[1-2]。此外，實(shí)際工程結(jié)構(gòu)的動(dòng)響應(yīng)問題一般是利用系統(tǒng)模態(tài)阻尼比求解，按照已有標(biāo)準(zhǔn)測(cè)試方法所得阻尼參數(shù)難以直接運(yùn)用，因此在尋找優(yōu)良的阻尼材料和結(jié)構(gòu)型式以實(shí)現(xiàn)減振降噪等效果的同時(shí)，探究可靠實(shí)用的阻尼測(cè)試方法也十分緊迫。

現(xiàn)階段特殊結(jié)構(gòu)的模態(tài)阻尼是通過試驗(yàn)?zāi)B(tài)分析來識(shí)別的，傳統(tǒng)的參數(shù)識(shí)別方法可在時(shí)域和頻域內(nèi)進(jìn)行。然而，諸如艦艇等復(fù)雜機(jī)械結(jié)構(gòu)的總振動(dòng)阻尼系數(shù)測(cè)試難度較大，時(shí)域衰減法僅能得到其低階阻尼系數(shù)，頻響曲線識(shí)別時(shí)又必須同時(shí)測(cè)量響應(yīng)與激勵(lì)的時(shí)序信號(hào)，激勵(lì)過小時(shí)遠(yuǎn)離激勵(lì)處響應(yīng)小、信噪比劣，加大激勵(lì)會(huì)造成局部響應(yīng)過大的非線性問題，若采用“多入多出”的測(cè)量方式又會(huì)使試驗(yàn)更加繁瑣。何況，試驗(yàn)中想直接測(cè)出大型結(jié)構(gòu)某些激勵(lì)（如階躍激勵(lì)、自激勵(lì)等）的時(shí)序信號(hào)往往也是不現(xiàn)實(shí)的[3]，這均為艦艇總振動(dòng)阻尼測(cè)試和動(dòng)響應(yīng)預(yù)報(bào)帶來了困難。

此外，隨著艦艇振聲計(jì)算要求的提高，僅得到全船總振動(dòng)阻尼時(shí)常不能滿足設(shè)計(jì)師需求，人們開始關(guān)心局部振動(dòng)及其噪聲輻射情況，針對(duì)性地對(duì)噪聲較大區(qū)域使用阻尼材料進(jìn)行控制，因此在該背景下對(duì)局部殼體板單元阻尼測(cè)試精度提出了更高要求，以指導(dǎo)分布式阻尼設(shè)計(jì)。然而現(xiàn)有試驗(yàn)方法亦存在識(shí)別缺陷，常用的頻域測(cè)力法中包括單自由度圖解法（如峰值拾取法、導(dǎo)納圓法）和多自由度解析法（如各類擬和法），分別適用于模態(tài)稀疏的小阻尼結(jié)構(gòu)和模態(tài)密集的大阻尼結(jié)構(gòu)。陳奎孚等[4-5]和應(yīng)懷樵等[6]對(duì)峰值拾取法中半功率理論誤差進(jìn)行了分析，結(jié)果表明受半功率點(diǎn)識(shí)別誤差、窗阻尼誤差以及不同信號(hào)處理手段差異等因素影響，阻尼估算值較實(shí)際值偏差可達(dá)幾倍甚至幾十倍；導(dǎo)納圓法計(jì)算精度受圖解精度的限制，且無法避免因鄰近模態(tài)疊加所產(chǎn)生的誤差[7]。擬合解析法常處理多自由度系統(tǒng)，一般為得到密集模態(tài)的信息會(huì)增加測(cè)點(diǎn)數(shù)目，此舉措既增大計(jì)算量也易產(chǎn)生病態(tài)轉(zhuǎn)換矩陣，從而影響參數(shù)識(shí)別精度[8]。多自由度系統(tǒng)時(shí)域下的參數(shù)識(shí)別需使用窗函數(shù)對(duì)信號(hào)濾波處理，經(jīng)典窗在分離低頻密集模態(tài)和疊加模態(tài)時(shí)精度較差，特別是位于頻響函數(shù)的兩端且很接近的模態(tài)[9-10]。

為對(duì)艦艇總振動(dòng)模態(tài)阻尼測(cè)試提供簡(jiǎn)便可行的方法，對(duì)局部船體板單元阻尼進(jìn)行更精確的識(shí)別，本文以結(jié)構(gòu)的實(shí)測(cè)響應(yīng)數(shù)據(jù)為基礎(chǔ)，提出了一種通過變頻激勵(lì)響應(yīng)反演系統(tǒng)模態(tài)阻尼比的計(jì)算方法，規(guī)避了某些激勵(lì)時(shí)序信號(hào)的測(cè)量難題。推導(dǎo)出多自由度系統(tǒng)共振頻率及其鄰近頻率激勵(lì)下的響應(yīng)與阻尼比之間的理論關(guān)系，指出試驗(yàn)中若忽視共振響應(yīng)與最大響應(yīng)間的差異，往往會(huì)造成某些計(jì)算結(jié)果的大幅偏差，給出了“響應(yīng)比”、“復(fù)合比例因子”的概念，并總結(jié)了提高該阻尼反演理論計(jì)算精度的相關(guān)規(guī)律。以某船全船船體梁為例，結(jié)合規(guī)范驗(yàn)證了阻尼反演理論及其識(shí)別公式的可靠性，并對(duì)該理論進(jìn)行二維推廣，完成了4塊不同型式的局部船體板單元模型的阻尼比試驗(yàn)測(cè)試，為潛艇總振動(dòng)阻尼估算方法以及分布式阻尼設(shè)計(jì)提供了可靠的技術(shù)支撐。

1 阻尼反演計(jì)算理論

1.1 總振動(dòng)響應(yīng)的模態(tài)表達(dá)

在研究多自由度系統(tǒng)響應(yīng)問題時(shí)，一般采用模態(tài)疊加法，文中以一維梁模型進(jìn)行推導(dǎo)，得到共振頻率及其鄰近頻率激勵(lì)下系統(tǒng)總響應(yīng)表達(dá)式。本反演計(jì)算理論推廣到二維平面、三維空間系統(tǒng)時(shí)，應(yīng)對(duì)外加激勵(lì)力、質(zhì)量矩陣和模態(tài)振型等參數(shù)的一維變量進(jìn)行二、三維替換。一維梁在外加激勵(lì)力F( x,t )作用下的總振動(dòng)響應(yīng)為[11]

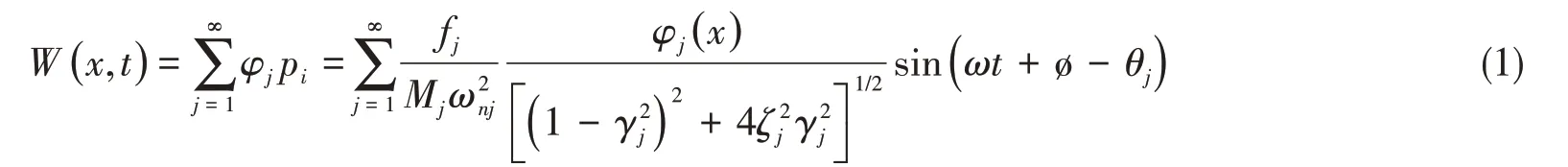
其中：

式中，Mj、φj、fj和ζj分別為第j階廣義質(zhì)量、振型、模態(tài)力和模態(tài)阻尼比，γj為激振力頻率ω與第j階固有頻率ωnj的頻率比。

一維梁在外加激勵(lì)力作用下發(fā)生第j 階共振時(shí)，其主模態(tài)響應(yīng)遠(yuǎn)大于其它階模態(tài)響應(yīng)，故一維梁的該階共振總響應(yīng)可記為

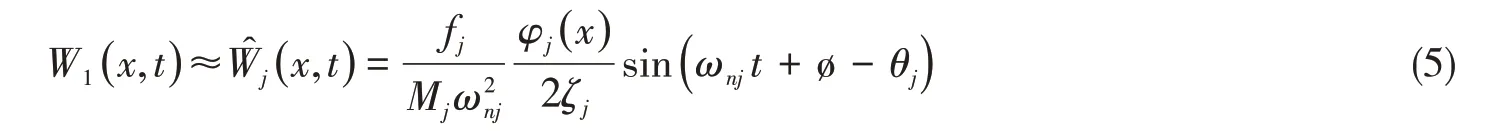
改變激勵(lì)力頻率ω，使其與一維梁第j階固有頻率ωnj有一小量的差別Δω，則響應(yīng)為

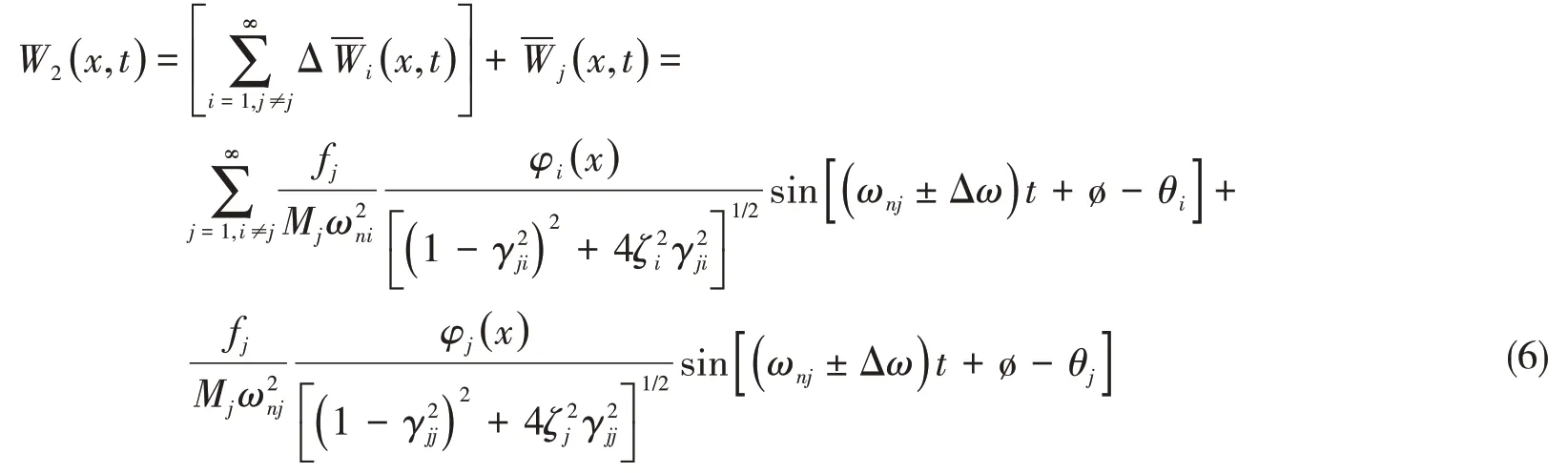
其中，推廣頻率比γji為第j 階固有頻率鄰近激振頻率與第i 階固有頻率之比，即γji=( ωnj±Δω )/ωni。Δi( x,t )為ωnj±Δω頻率激勵(lì)下第i階模態(tài)響應(yīng)分量( x,t )為第j階主模態(tài)穩(wěn)態(tài)響應(yīng)分量（非共振響應(yīng)）。

其中，

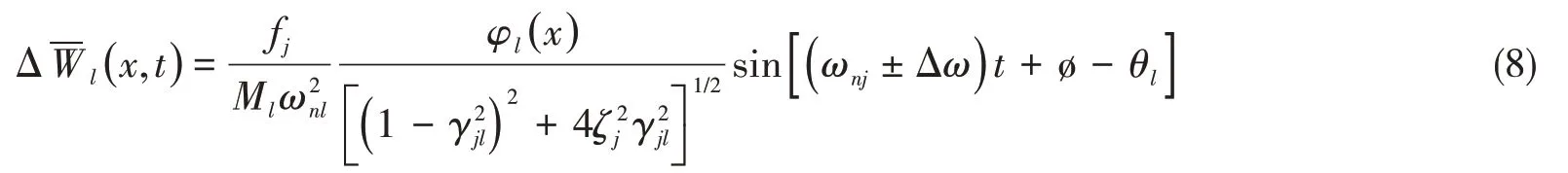
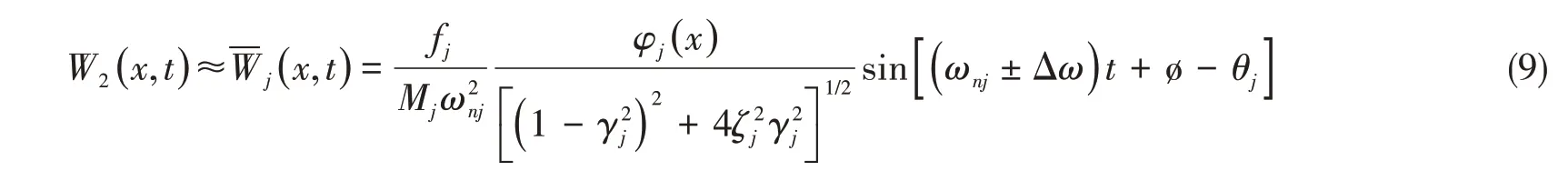
為簡(jiǎn)化表達(dá)，使γjj= γj=( ωnj±Δω )/ωnj。當(dāng)外加激勵(lì)力F( x,t )為作用于點(diǎn)的集中力時(shí)，即：

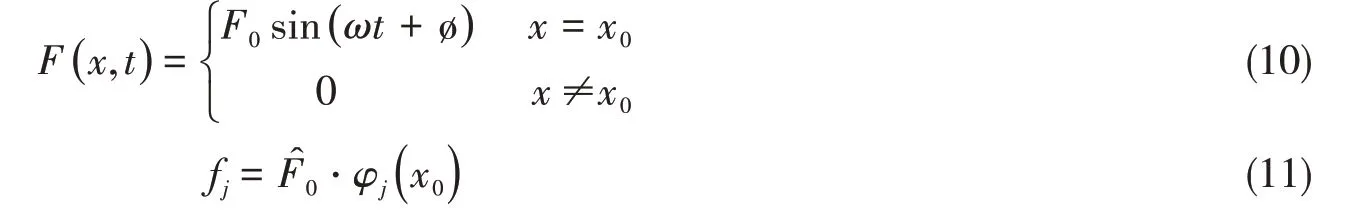
則（5）式為

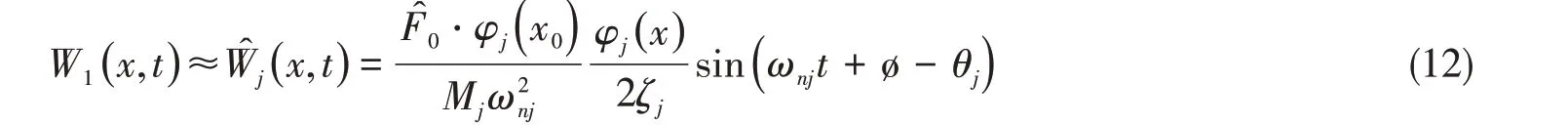
測(cè)點(diǎn)位于振型“節(jié)點(diǎn)”的（9）式可表示為

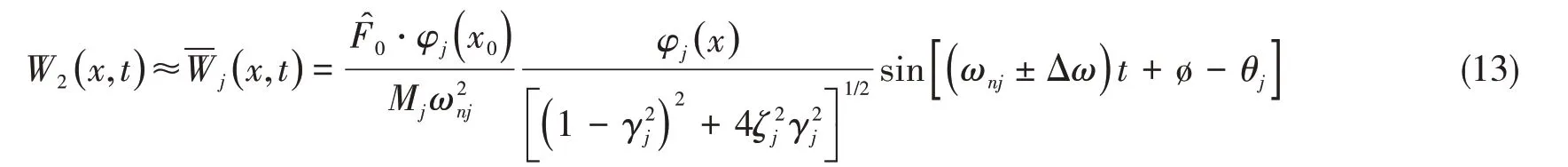
1.2 恒定激勵(lì)力激起共振響應(yīng)的阻尼比反演算法

按ωnj± Δω 和ωnj頻率激勵(lì)（激勵(lì)力幅相同）時(shí)，系統(tǒng)第j 階主模態(tài)穩(wěn)態(tài)響應(yīng)幅值-Wj( x )和共振響應(yīng)幅值Wj( x )之比，記作δj，定義為“響應(yīng)比”。

由（7）式、（12）-（13）式可得：

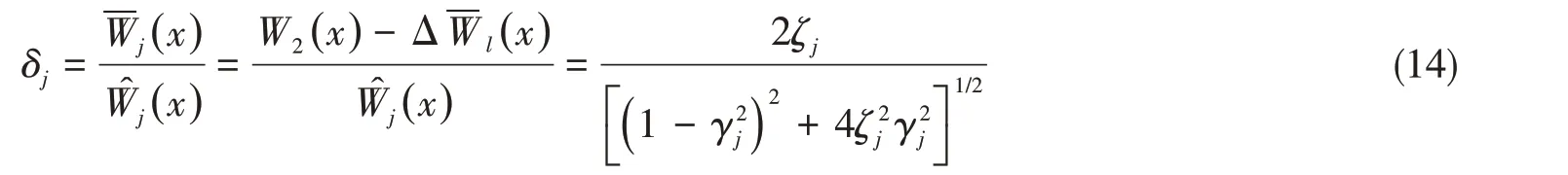
則

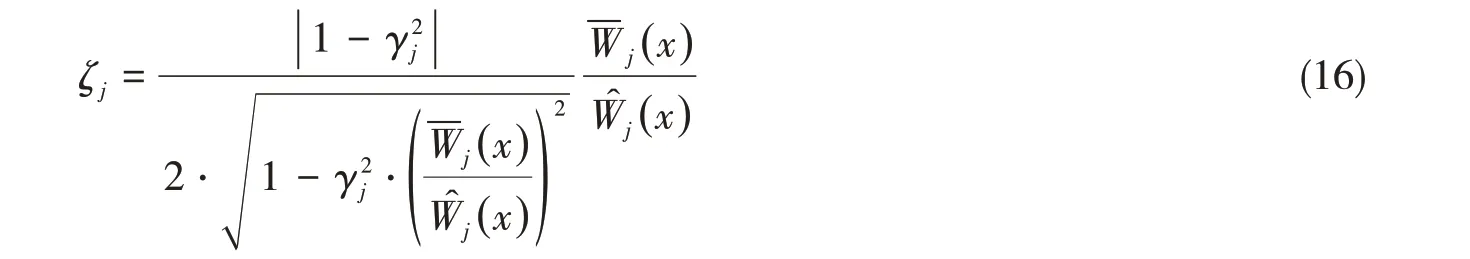
定義頻率比γj與響應(yīng)比δj的乘積為“復(fù)合比例因子”，以描述二者疊乘的復(fù)比例效應(yīng)，用χj表示。則

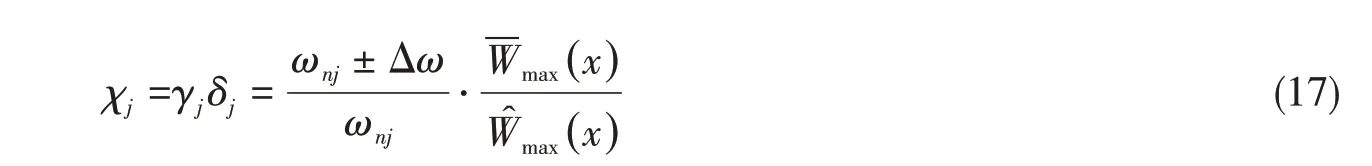
結(jié)合χ定義，（16）式可改寫為

圖1 給出了以χ 為變量的共振響應(yīng)反演阻尼曲線，其中，Δω 分別取2%ωnj、5%ωnj和10%ωnj進(jìn)行錯(cuò)頻計(jì)算，則γj=0.9、0.95、0.98、1.02、1.05、1.1。此外，由于實(shí)際結(jié)構(gòu)存在阻尼，則( x )/( x )<1。

由圖中可知，頻率小幅錯(cuò)開下，阻尼識(shí)別結(jié)果隨χ 增大而增大，在研究區(qū)域內(nèi)具有“類反比例”增函數(shù)的規(guī)律。令阻尼函數(shù)ζ( χ,γ )進(jìn)行一、二階的對(duì)χ 偏導(dǎo)計(jì)算，曲線斜率變化率為二階偏導(dǎo)?2ζ( χ,γ )/?χ2>0，曲線為凹。根據(jù)三階偏導(dǎo)?3ζ( χ,γ )/?3χ = 0 來計(jì)算曲線斜率變化率的極值點(diǎn)，該點(diǎn)為,～ζj)，在圖1 中標(biāo)出。在χj∈é? 0ù?范圍內(nèi)，曲線平緩、斜率小，試驗(yàn)測(cè)量時(shí)響應(yīng)比δj難以避免的小量誤差并不會(huì)造成過大的阻尼比計(jì)算偏差，因此根據(jù)圖中曲線性質(zhì)，響應(yīng)比δj越小（即χ 越小）、Δω 越小時(shí)曲線斜率越小，此時(shí)更易于得到精度可靠的阻尼比結(jié)果。

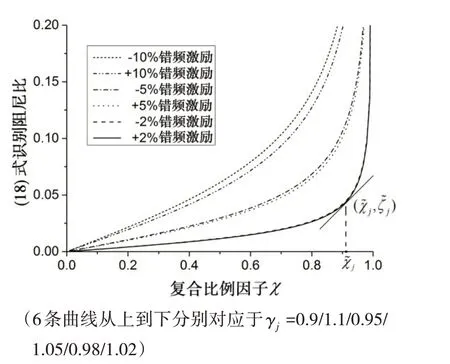
圖1（18）式識(shí)別阻尼比曲線Fig.1 Damping ratio curves identified by Eq.(18)

1.3 應(yīng)用模態(tài)最大位移響應(yīng)的阻尼比反演算法

試驗(yàn)測(cè)試時(shí)，時(shí)常以最大響應(yīng)值所對(duì)應(yīng)的激勵(lì)頻率為結(jié)構(gòu)固有頻率，即認(rèn)為最大響應(yīng)為某階模態(tài)共振響應(yīng)，實(shí)際上模態(tài)最大響應(yīng)是大于該階模態(tài)共振響應(yīng)的。（18）式是在模態(tài)共振響應(yīng)基礎(chǔ)上推導(dǎo)的，以下按第j階模態(tài)最大響應(yīng)和第j階模態(tài)在鄰近頻率處非共振穩(wěn)態(tài)響應(yīng)推導(dǎo)該階模態(tài)阻尼比。第j階最大振動(dòng)響應(yīng)對(duì)應(yīng)的峰值頻率與第j階固有頻率之比為：

一維梁在外加激勵(lì)力作用下使第j 階模態(tài)產(chǎn)生最大響應(yīng)，按（12）式類推得總響應(yīng)為

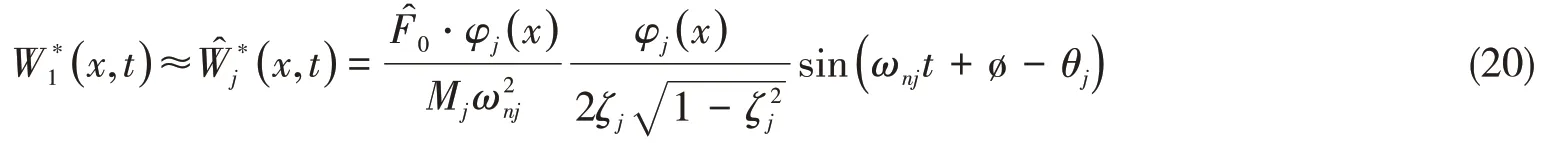
由（14）式類推得：

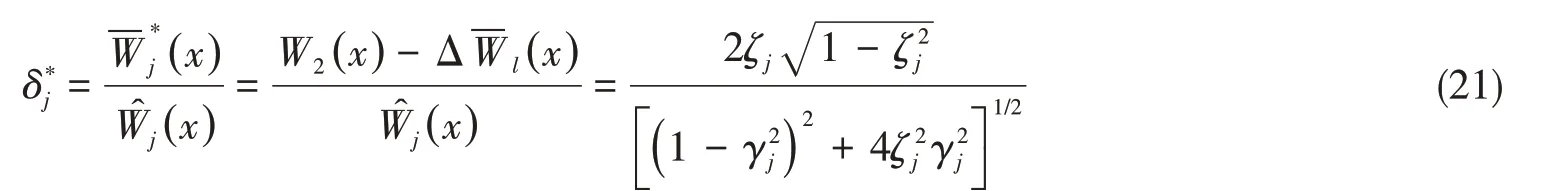
若γ峰j= 1，模態(tài)響應(yīng)出現(xiàn)最大值，此時(shí)ζj= 0。此時(shí)判斷唯一可行解為

與1.2節(jié)類似，構(gòu)造相同的變量范圍，阻尼比識(shí)別公式曲線如圖2所示。

曲線趨勢(shì)及規(guī)律與圖1所示相似，但當(dāng)c 較大時(shí)，兩圖在阻尼比計(jì)算結(jié)果上差別較大，有必要對(duì)ζj按（18）式和（22）式的計(jì)算相對(duì)偏差進(jìn)行分析。圖3給出了兩者相對(duì)偏差曲線，偏差量用ε表示為

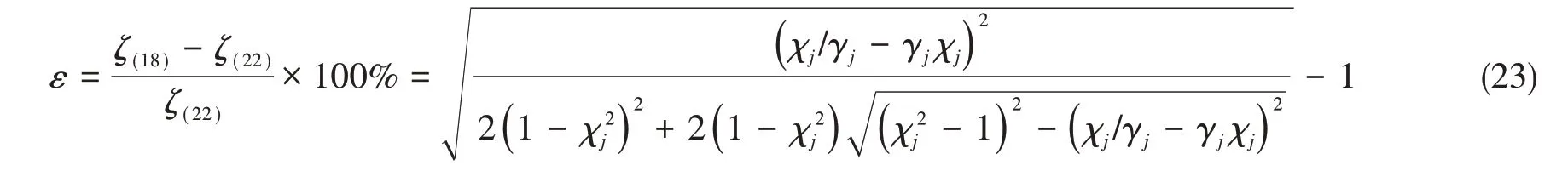
從圖3可見：

（1）相對(duì)偏差ε均為負(fù)偏差，則按（18）式所得阻尼比結(jié)果均小于（22）式計(jì)算結(jié)果；

（2）當(dāng)χ較小時(shí)（χj∈é? ù?0,），兩者阻尼比計(jì)算相對(duì)偏差很小，而隨χj增大，特別是當(dāng)響應(yīng)比δj趨近1時(shí)（即χj≈γj），相對(duì)偏差急劇增大，可以認(rèn)為γj確定時(shí)，阻尼越大，兩式計(jì)算相對(duì)偏差越大；

（3）圖中γj= 1±0.02、1±0.05、1±0.1 這三組曲線依次自上而下分布，可見當(dāng)Δω 較大時(shí)二者偏差大，且負(fù)向錯(cuò) 頻激勵(lì)（γj=( ωnj- Δω/ωnj)）計(jì)算結(jié)果 的 相對(duì)偏差 要 大于正向 錯(cuò) 頻激勵(lì)（γj=( ωnj+ Δω/ωnj)）。

因此，當(dāng)阻尼比較小、錯(cuò)頻幅值Δω不大時(shí)，兩式的結(jié)果相差不大，反之，則需要采用（22）式才能得到更精確的阻尼比反演結(jié)果。可見，在某些情況下，若忽視模態(tài)共振響應(yīng)與最大響應(yīng)的差異，往往會(huì)造成計(jì)算結(jié)果的大幅偏差。

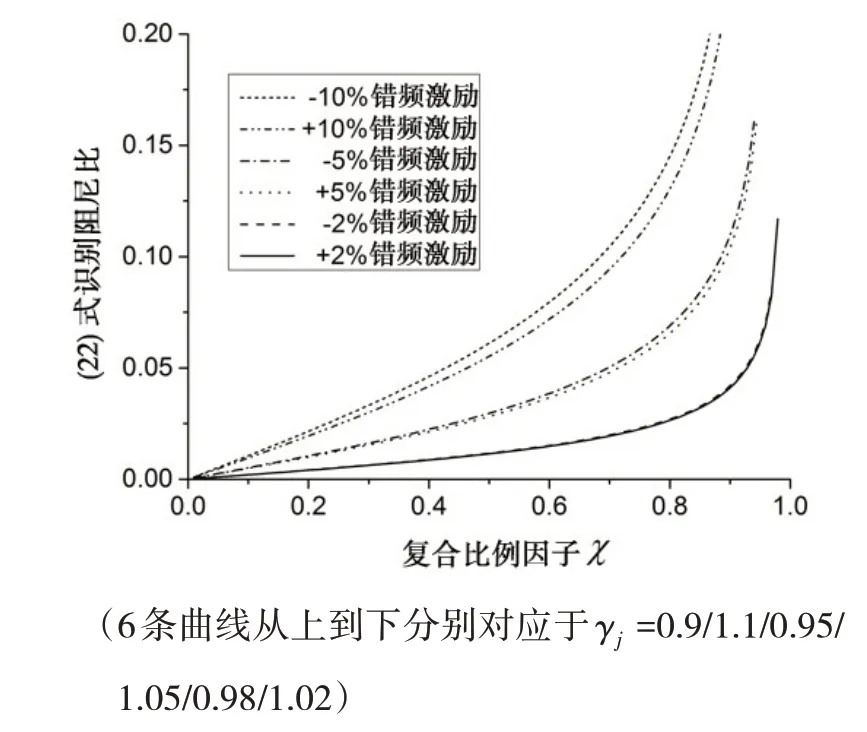
圖2（22）式識(shí)別阻尼比曲線 Fig.2 Damping ratio curves identified by Eq.(22)

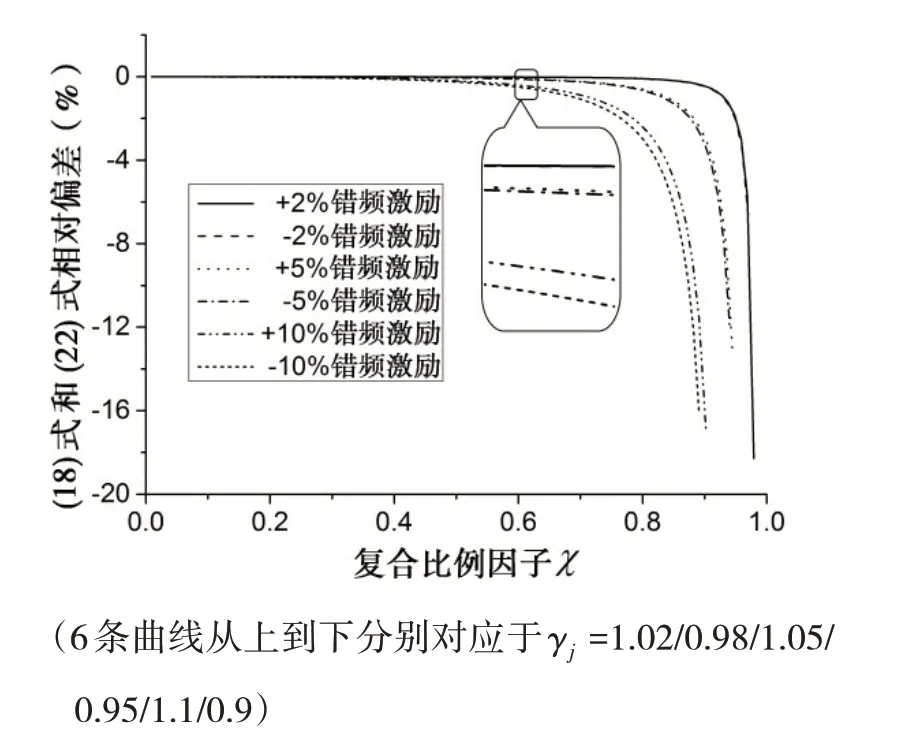
圖3（18）式和（22）式識(shí)別阻尼比的相對(duì)偏差曲線Fig.3 Relative deviation curves of damping ratio identified by Eqs.(18)and(22)

2 全船船體梁阻尼比反演理論有限元驗(yàn)證

反演理論阻尼參數(shù)的計(jì)算最終要通過試驗(yàn)的振動(dòng)響應(yīng)測(cè)試來完成。船舶工程領(lǐng)域中，處理全船總振動(dòng)常采用船體梁理論，為直接驗(yàn)證阻尼識(shí)別公式的準(zhǔn)確性，本文建立了某船全船船體梁有限元模型，模擬螺旋槳的變頻激勵(lì)完成該船的響應(yīng)獲取，進(jìn)而反演得到模態(tài)阻尼比。該船相關(guān)尺度參數(shù)見表1。

船體梁是一根變截面的主船體結(jié)構(gòu)等值梁，船體清晰具有船體梁的彎曲變形特征時(shí)為“似梁”彎曲。而振動(dòng)階次較高時(shí)，彎曲振動(dòng)的節(jié)點(diǎn)間距接近于或小于船寬和型深，常導(dǎo)致“非梁”的振動(dòng)特性，因此本例對(duì)船體前3階低階總振動(dòng)進(jìn)行響應(yīng)計(jì)算，將反演阻尼比值與設(shè)定值比對(duì)以驗(yàn)證理論。

舷外水對(duì)船體振動(dòng)的影響表現(xiàn)在重力、阻尼和慣性三個(gè)方面。靜水面附近振動(dòng)的浮力變化較小可忽略重力影響；船體強(qiáng)迫振動(dòng)位于共振區(qū)時(shí)需考慮阻尼，將其與內(nèi)阻尼合并考慮，按照規(guī)范中關(guān)于水面艦艇模態(tài)阻尼系數(shù)的規(guī)定[12]，見圖4（取低阻尼）；附漣水質(zhì)量導(dǎo)致船體慣性變化對(duì)船體總振動(dòng)影響較大，模型通過集中質(zhì)量點(diǎn)模擬其全船分布。按0～20 站號(hào)將船體分為20 段，計(jì)算各剖面要素（包括剖面慣性矩、各系數(shù)參量等）完成變截面船體梁的構(gòu)建。

以螺旋槳為激勵(lì)源，作用于船體艉部，變頻激勵(lì)時(shí)控制激勵(lì)力幅值相同，按1 kN 計(jì)算。根據(jù)上節(jié)討論中，按（22）式估算阻尼時(shí)，控制Δω 足夠小可獲得滿意的精度，數(shù)值計(jì)算中取2%的頻率增減量。對(duì)船體梁水平約束計(jì)算其垂向振動(dòng)，有限元振型見圖5。

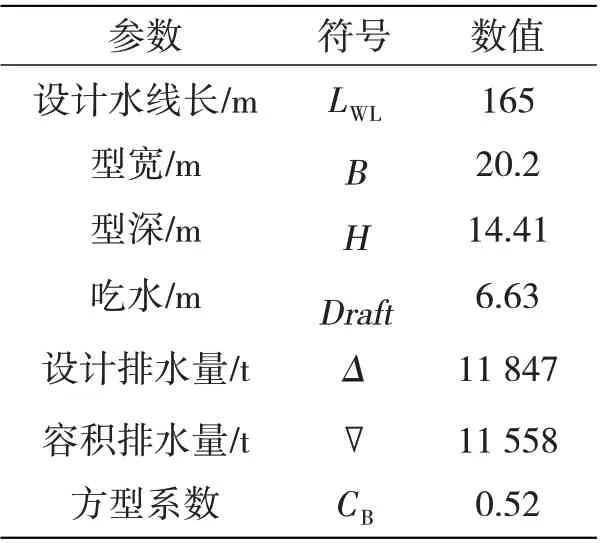
表1 某船主尺度參數(shù)Tab.1 Main scale parameters of a vessel

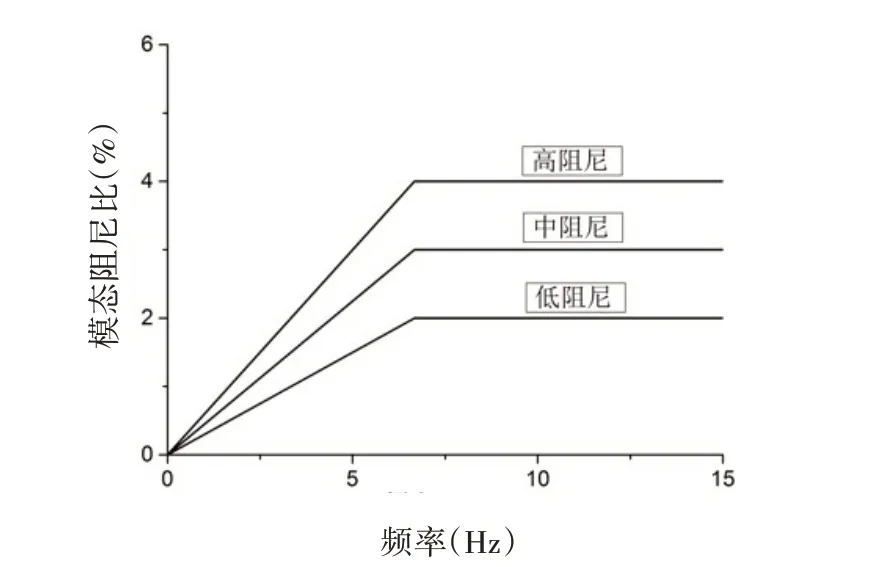
圖4 水面艦艇模態(tài)阻尼系數(shù) Fig.4 The modal damping coefficients of surface ship

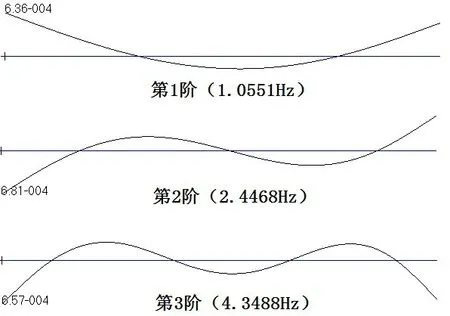
圖5 船體梁有限元振型圖Fig.5 Vibration diagram of finite element hull girder

經(jīng)模態(tài)計(jì)算，船體梁的前3階垂向固有頻率見表2，對(duì)表中3種工況進(jìn)行船體梁變頻振動(dòng)的數(shù)值計(jì)算，驗(yàn)證上述阻尼比測(cè)試方法和公式的可靠性。

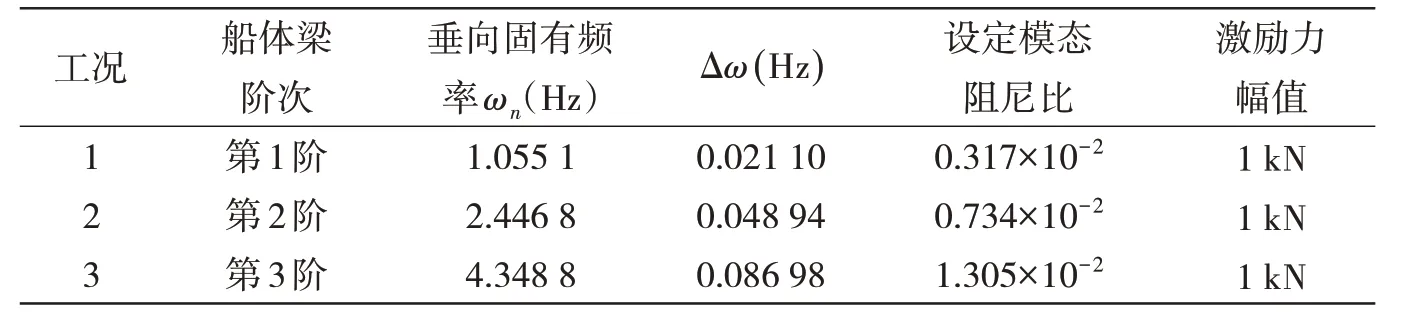
表2 數(shù)值計(jì)算參數(shù)Tab.2 Parameters of numerical calculation

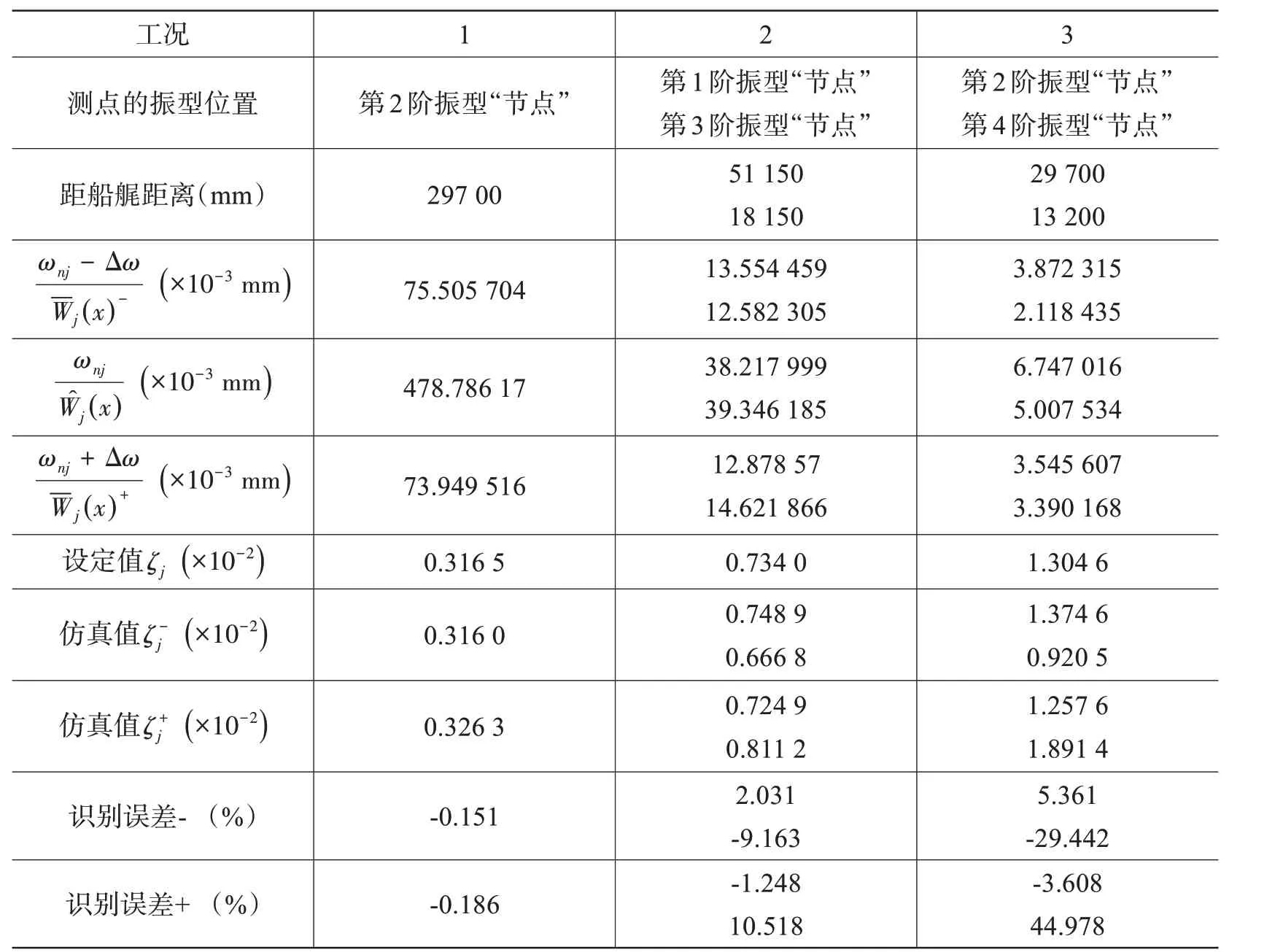
表3 阻尼反演計(jì)算結(jié)果及識(shí)別誤差Tab.3 Damping calculation results of inverse theory and identification error

對(duì)該船體梁進(jìn)行上述3組工況的強(qiáng)迫振動(dòng)響應(yīng)分析，得到共振頻率ωnj激勵(lì)下最大響應(yīng)( x )與鄰近共振頻率ωnj±Δω 激勵(lì)下穩(wěn)態(tài)響應(yīng)( x)±，測(cè)點(diǎn)布置在每階工況下鄰近階次的“節(jié)點(diǎn)”處（距船艉最近節(jié)點(diǎn)），按2%的變頻幅度，即γj= ωnj±Δω/ωnj= 1±0.02。（22）式計(jì)算所得模態(tài)阻尼比結(jié)果及其與設(shè)定值相對(duì)誤差見表3。

可見，對(duì)于該船體梁模型，測(cè)點(diǎn)位置的選擇對(duì)于阻尼比計(jì)算結(jié)果影響較大，但遵循一些規(guī)律。對(duì)于首階激勵(lì)工況1，以第2 階振型“節(jié)點(diǎn)”為測(cè)點(diǎn)，仿真阻尼識(shí)別誤差不超過0.2%，結(jié)果十分精確；對(duì)于較高階次的第2、3階激勵(lì)工況2、3，分別以各自相鄰階次振型的“節(jié)點(diǎn)”為測(cè)點(diǎn)，阻尼比結(jié)果具有3個(gè)顯著特征：

（1）隨著計(jì)算工況階次的升高，仿真阻尼比識(shí)別誤差呈一定程度的線性增大，這與之前描述的船體在振動(dòng)階次較高時(shí)易產(chǎn)生“非梁”的振動(dòng)特性一致；

（2）工況2、3 中按相鄰較低階振型“節(jié)點(diǎn)”所測(cè)響應(yīng)計(jì)算的阻尼比更準(zhǔn)確，最大誤差為5.36%。文獻(xiàn)[13]推導(dǎo)了特殊懸臂梁按第1、2 階共振頻率激勵(lì)時(shí)的響應(yīng)表達(dá)式，認(rèn)為較高階（即第2 階）共振激勵(lì)下懸臂梁低階模態(tài)位移的貢獻(xiàn)比例會(huì)增大，在小阻尼情況下以低階（即第1 階）共振頻率激勵(lì)時(shí)響應(yīng)仍主要來源于當(dāng)前模態(tài)貢獻(xiàn)。因此考慮仿真計(jì)算中，較高階次工況應(yīng)按相鄰低階振型“節(jié)點(diǎn)”所測(cè)響應(yīng)來計(jì)算阻尼比，這能減小低階模態(tài)成分的影響以提高計(jì)算精度；

因此，船舶在平穩(wěn)水域航行試驗(yàn)時(shí)改變螺旋槳轉(zhuǎn)速便可實(shí)現(xiàn)激勵(lì)的小幅錯(cuò)開和響應(yīng)采集，進(jìn)一步可通過反演理論估算出船體總振動(dòng)模態(tài)阻尼比。

3 局部船體板單元阻尼比反演理論試驗(yàn)驗(yàn)證

3.1 試驗(yàn)背景及環(huán)境

潛艇在實(shí)際建造時(shí)板殼材質(zhì)、厚度等在全船范圍內(nèi)分布復(fù)雜，直接用船體總振動(dòng)阻尼對(duì)其進(jìn)行響應(yīng)和振聲性能預(yù)報(bào)時(shí)常偏離實(shí)際且誤差較大。淡丹輝等[14]提出單元化的阻尼比法則在控制結(jié)構(gòu)總體模態(tài)阻尼比方面更具優(yōu)勢(shì)，可在對(duì)多階模態(tài)阻尼比精確控制的同時(shí)又能解決分布式阻尼的建模問題。為對(duì)潛艇輻射噪聲進(jìn)行更加準(zhǔn)確的預(yù)報(bào)，對(duì)聲輻射顯著的局部區(qū)域采取必要的控制，因此在計(jì)算殼體表面振動(dòng)響應(yīng)前應(yīng)了解其阻尼分布情況，有必要對(duì)船體典型板單元結(jié)構(gòu)進(jìn)行阻尼比測(cè)試，以實(shí)現(xiàn)復(fù)雜阻尼分布的總體估計(jì)。此外，復(fù)合材料在降低潛艇聲輻射方面有誘人的應(yīng)用前景，可見研究其與鋼材的阻尼性能差異尤為重要。

按照現(xiàn)行規(guī)范，在進(jìn)行整船結(jié)構(gòu)有限元建模時(shí)板殼網(wǎng)格尺寸常按一個(gè)縱骨或一個(gè)肋位間距（500 mm 左右）小者劃分，且盡量接近正方形。本試驗(yàn)依據(jù)規(guī)范對(duì)網(wǎng)格尺度的要求，布置典型板單元阻尼比試驗(yàn)測(cè)試模型如圖6 所示。構(gòu)造固定的邊界條件以模擬板在實(shí)船中與周圍肋骨等骨架的連接狀況，用24 根螺栓將板緊固在基座與壓條之間，注入玻璃膠填充縫隙以防止頻段內(nèi)漏聲造成的誤差。為避免試驗(yàn)激勵(lì)時(shí)板帶動(dòng)基座產(chǎn)生耦合共振現(xiàn)象，基座使用15 mm 厚度鋼塊焊制并在四周設(shè)置支撐結(jié)構(gòu)以增加其質(zhì)量和剛度，控制其首階自振頻率在1 kHz 以上，保證與各板單元模型前8 階自振頻率有足夠的錯(cuò)開率。

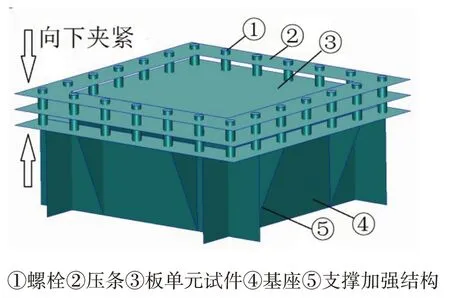
圖6 試驗(yàn)?zāi)Ｐ涂臻g示意圖（測(cè)試內(nèi)區(qū)域500 mm×500 mm）Fig.6 Experimental model spatial schematic diagram(test area 500 mm×500 mm)

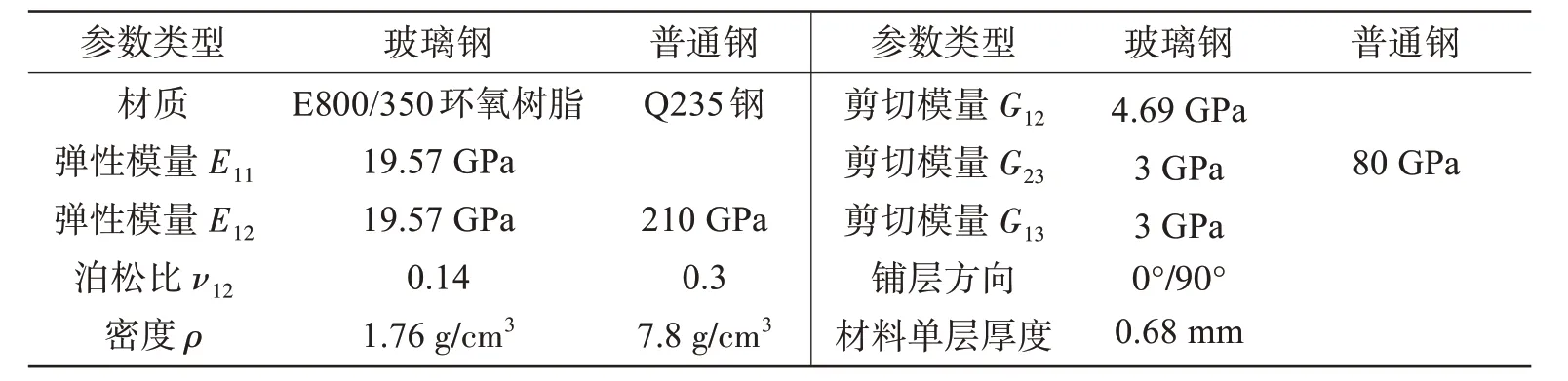
表4 玻璃鋼板與普通鋼板材料性能參數(shù)Tab.4 Material performance parameters of glass fiber plate and common steel plate

復(fù)合材料的性能與鋼材差異較大，本試驗(yàn)使用2D 正交各向異性復(fù)合材料，相關(guān)參數(shù)在表4 中給出。依據(jù)該參數(shù)，試驗(yàn)分別對(duì)500 mm×500 mm×3 mm 規(guī)格Q235 鋼板及與其等厚度、等剛度、等質(zhì)量的3 塊E800/350 環(huán)氧樹脂材質(zhì)的玻璃鋼板進(jìn)行多階模態(tài)阻尼比識(shí)別，并探究復(fù)合材料與鋼材在阻尼性能上的規(guī)律。板單元試驗(yàn)?zāi)Ｐ统叨葏?shù)見表5。

表5 板單元試驗(yàn)?zāi)Ｐ统叨葏?shù)Tab.5 Experimental model scale parameters of plate unit

3.2 板單元模型阻尼試驗(yàn)及結(jié)果分析

用共振駐留法對(duì)結(jié)構(gòu)進(jìn)行各階共振及其鄰近頻率激勵(lì)，得到測(cè)點(diǎn)時(shí)序響應(yīng)曲線，傳感器的布置根據(jù)事先進(jìn)行的模態(tài)分析確定，使之盡量既位于其鄰近低階階次的振型“節(jié)點(diǎn)”或“節(jié)線”處，亦為該階振型下具有明顯響應(yīng)的位置。考慮微幅振動(dòng)下加速度響應(yīng)信號(hào)比較顯著，所有測(cè)點(diǎn)均用加速度傳感器采集，采集穩(wěn)態(tài)振動(dòng)后一段時(shí)長(zhǎng)的數(shù)據(jù)，并對(duì)響應(yīng)進(jìn)行力幅歸一化處理。在單元模型上設(shè)置9個(gè)測(cè)點(diǎn)位置，激勵(lì)試驗(yàn)如圖7所示。

圖7 共振激勵(lì)試驗(yàn)（玻璃鋼板） Fig.7 Resonance excitation experiment(glass fiber plate)

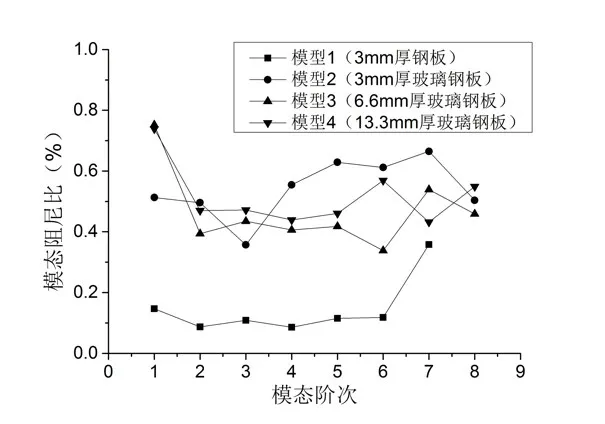
圖8 模型1～4各模態(tài)阻尼比測(cè)算結(jié)果對(duì)比Fig.8 Estimated testing modal damping ratio of model Nos.1～4

單點(diǎn)拾振法的脈沖激勵(lì)試驗(yàn)可以得到板單元模型的固有頻率和模態(tài)振型，依據(jù)模態(tài)識(shí)別結(jié)果設(shè)計(jì)激振頻率及測(cè)點(diǎn)布置，反演理論中位移“響應(yīng)比”與加速度（用A表示）“響應(yīng)比”的數(shù)值是相等的，表6給出了板單元模型2試驗(yàn)響應(yīng)及阻尼反演結(jié)果。4塊不同板單元模型按反演理論所測(cè)阻尼比數(shù)值對(duì)比見表7，模型1～4各模態(tài)阻尼比測(cè)算結(jié)果對(duì)比見圖8。

對(duì)比表7中各板單元阻尼比識(shí)別結(jié)果，可見復(fù)合材料板的阻尼性能總體上大于鋼板，除個(gè)別較高階階次外，試驗(yàn)中所用復(fù)合材料板的各階模態(tài)阻尼比約為鋼板的4～5倍。邊界約束條件相同時(shí)，二維空間下方形薄板振型規(guī)律基本一致，從表中計(jì)算數(shù)據(jù)可見，同種材質(zhì)下厚度對(duì)板格結(jié)構(gòu)的模態(tài)阻尼比大小影響不大，模型2～4 的各階模態(tài)阻尼比約為0.4%～0.5%，模型1（鋼板）則約為0.1%。此外，由圖8可見，與模型1等厚度、等靜剛度及等質(zhì)量的玻璃鋼板，各階對(duì)應(yīng)測(cè)點(diǎn)共振響應(yīng)均大幅降低，其中模型4（與鋼板等質(zhì)量）加速度各階共振響應(yīng)幅值僅為鋼板的1/5 左右。因此，大阻尼、低密度、高比剛度的復(fù)合材料結(jié)構(gòu)，在控制系統(tǒng)振動(dòng)及噪聲輻射方面具有較好的應(yīng)用前景。

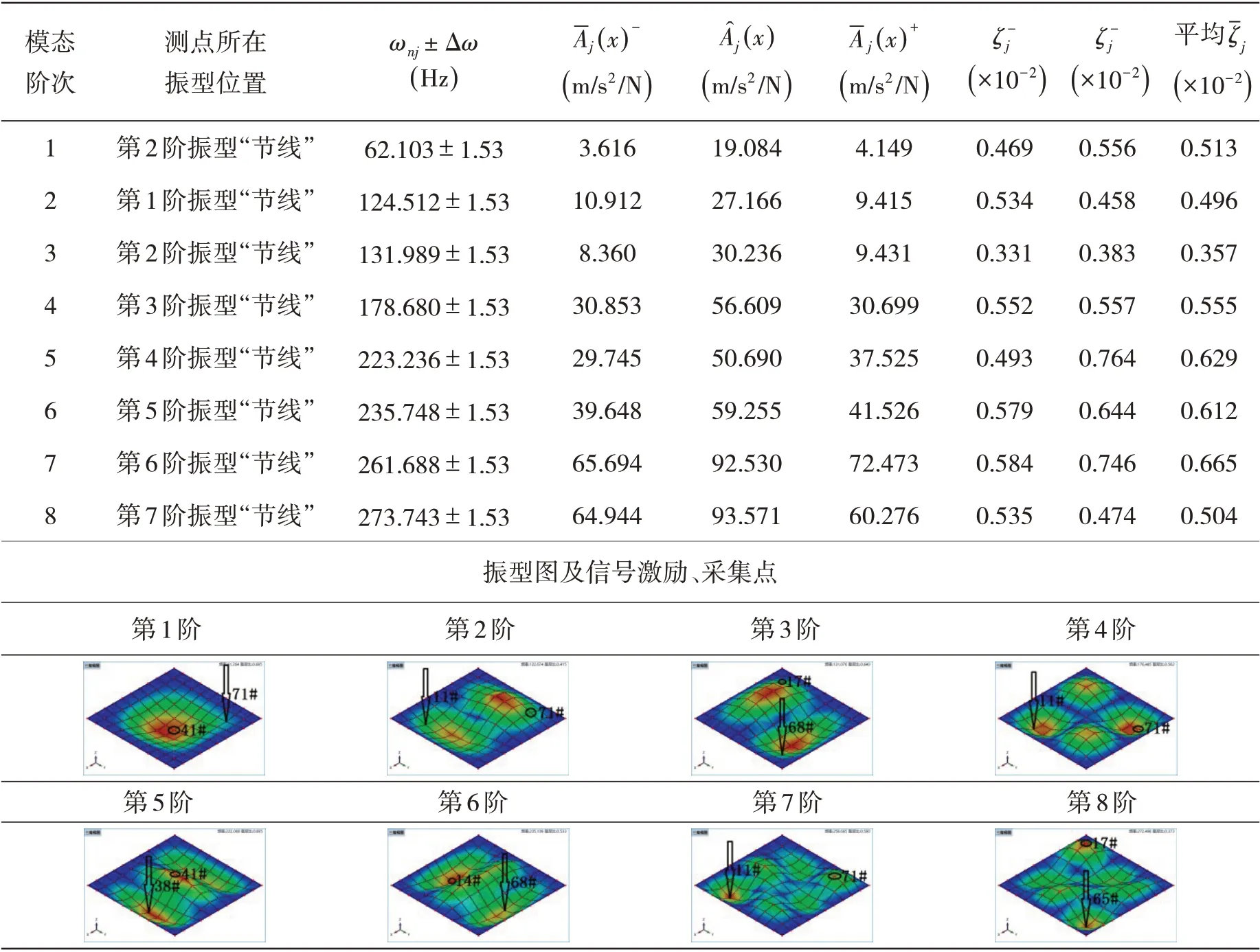
表6 板單元模型阻尼反演計(jì)算結(jié)果（模型2）Tab.6 Damping results of plate unit model calculated by inverse theory(Pattern number 2)

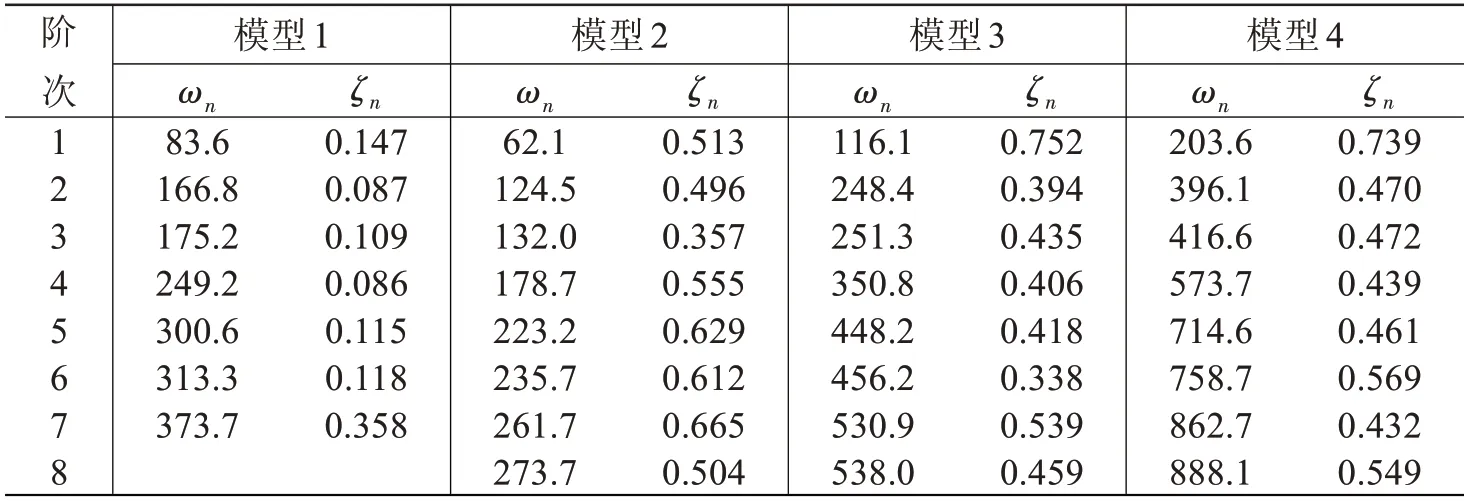
表7 玻璃鋼板與普通鋼板模型固有頻率及估算阻尼Tab.7 Natural frequency and the estimated damping coefficient of glass fiber plate and common steel plate model

3.3 阻尼反演結(jié)果數(shù)值計(jì)算驗(yàn)證

為驗(yàn)證阻尼結(jié)果的可靠性，以11#與71#測(cè)點(diǎn)間頻響函數(shù)為例，對(duì)4塊板的脈沖激勵(lì)試驗(yàn)所得寬頻帶響應(yīng)數(shù)據(jù)進(jìn)行分析，將其與該頻段數(shù)值計(jì)算頻響結(jié)果對(duì)比。以模型1～2 為例，頻響曲線對(duì)比如圖9所示。

圖中實(shí)線部分給出了按反演理論所得阻尼比ζj數(shù)值計(jì)算出的頻響曲線，將該曲線與試驗(yàn)數(shù)據(jù)比對(duì)可見，除因固有頻率微小差異導(dǎo)致的譜線峰值小幅偏移外，曲線在峰值大小、分布形狀上均與試驗(yàn)結(jié)果高度匹配，可認(rèn)為該理論所得阻尼比較為可靠。

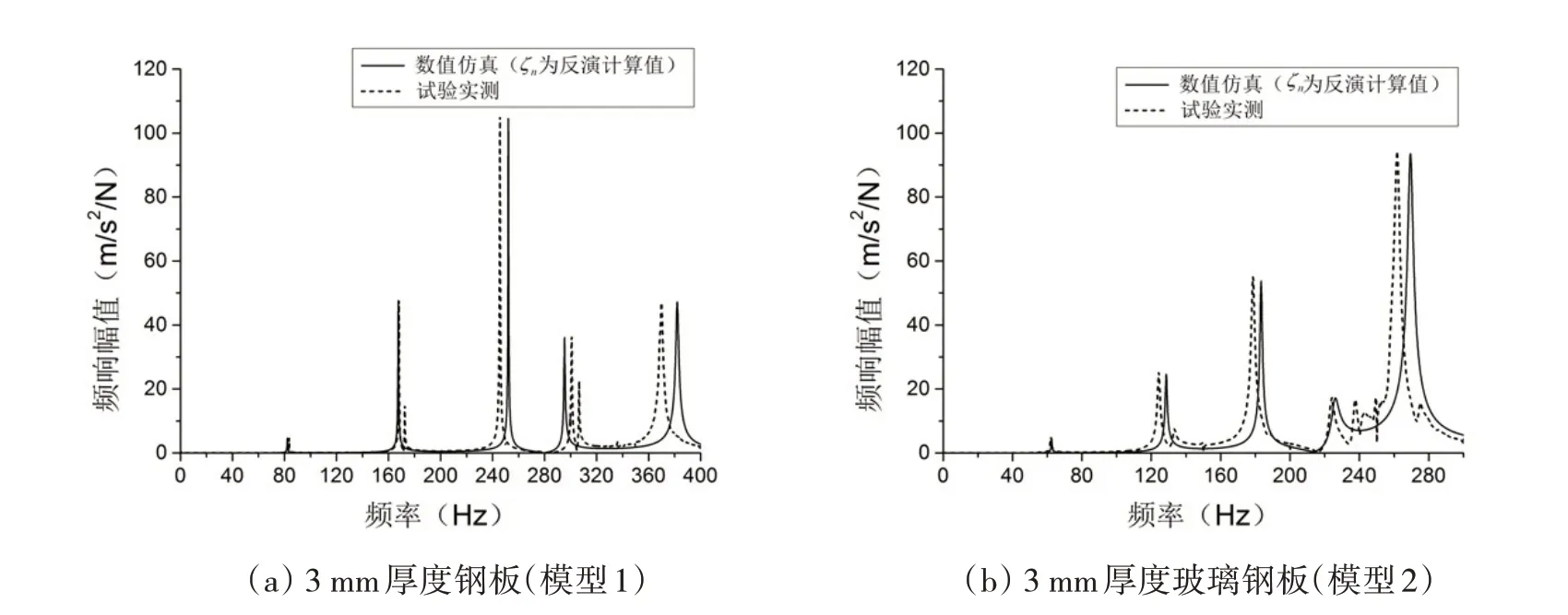
圖9 試驗(yàn)與數(shù)值計(jì)算寬頻帶頻響曲線對(duì)比Fig.9 Broadband frequency response comparison of experiment and numerical calculation

4 結(jié) 論

目前，系統(tǒng)模態(tài)阻尼比一般通過經(jīng)驗(yàn)規(guī)范或者傳統(tǒng)試驗(yàn)測(cè)試獲得，現(xiàn)有的資料和方法在處理實(shí)際工程結(jié)構(gòu)問題時(shí)具有一定的局限性。本文對(duì)阻尼研究的現(xiàn)狀和常用識(shí)別理論的缺陷進(jìn)行歸納，從經(jīng)典模態(tài)分析方法入手，推導(dǎo)出變頻激勵(lì)下的響應(yīng)與阻尼比的關(guān)系，提出“復(fù)合比例因子”的概念，并對(duì)該阻尼反演計(jì)算理論進(jìn)行分析。并且以某船船體梁為例進(jìn)行數(shù)值計(jì)算，驗(yàn)證了理論及公式的可靠性，為全船總振動(dòng)模態(tài)阻尼測(cè)試提供了簡(jiǎn)便可行的試驗(yàn)方法。基于阻尼反演理論曲線分析及船體梁數(shù)值計(jì)算結(jié)果，得到3條提高阻尼反演理論計(jì)算精度的規(guī)律：

（1）除首階工況外，其余較高階工況的測(cè)點(diǎn)應(yīng)盡量布置在相鄰低階振型“節(jié)點(diǎn)”（或“節(jié)線”）處；

（2）應(yīng)對(duì)共振頻率及其鄰近頻率激振響應(yīng)計(jì)算所得的阻尼比ζ±j進(jìn)行平均；

（3）應(yīng)控制變頻幅度Δω不能過大，在保證測(cè)試方案可行的情況下越小越好。

本文進(jìn)一步對(duì)該理論進(jìn)行了二維推廣，完成了幾塊不同型式復(fù)合材料船體板單元結(jié)構(gòu)的模態(tài)阻尼比試驗(yàn)測(cè)試，并與鋼板進(jìn)行比較，得到了如下結(jié)論：

（1）相同邊界條件及結(jié)構(gòu)振型下，薄板的材料是影響其模態(tài)阻尼比的主要因素，與厚度、剛度及質(zhì)量等關(guān)系不大；

（2）文中典型船體局部板單元結(jié)構(gòu)的各階模態(tài)阻尼比（鋼材）約為0.1%，復(fù)合材料板的阻尼性能要優(yōu)越于鋼板，玻璃鋼（E800/350環(huán)氧樹脂）的模態(tài)阻尼比約為鋼板的4～5倍。

因此，依據(jù)振動(dòng)響應(yīng)反演阻尼的算法，避免了采集激勵(lì)力的時(shí)域信號(hào)，操作簡(jiǎn)便、適用范圍廣，為船舶等大型結(jié)構(gòu)的總振動(dòng)阻尼測(cè)試提供了切實(shí)可行的方法，為局部結(jié)構(gòu)的精確阻尼比測(cè)試、利用分布式阻尼實(shí)現(xiàn)減振降噪的研究提供了新思路。