基于流固耦合方法的船舶破冰阻力參數敏感性研究

劉為民，涂勛程，谷家揚，陶延武，張忠宇

（1.江蘇科技大學船舶與海洋工程學院，江蘇鎮江212003；2.重慶前衛科技集團有限公司，重慶401121；3.江蘇科技大學海洋裝備研究院，江蘇鎮江212003）

0 引 言

北極航道商用價值日益顯著，冰區船舶航行逐年增加，船舶與冰層的作用過程屬于強非線性動力學和流固耦合問題，船舶破冰阻力的準確預報及其各敏感性參數對阻力變化影響的問題亟待解決。

國外學者在關于冰阻力方面的研究起步較早，早期主要采用經驗公式與解析相結合的方法評估冰阻力。基于不斷豐富的實船測量數據和模型試驗，相關學者對連續破冰過程的冰阻力計算提出了多種經驗公式和解析方法，其中，Lewis&Edwards公式、改進Lewis公式和改進Edwards公式形式類似、參數較少，僅考慮了船寬、冰厚及航速對冰阻力的影響。Lindqvist[1]結合實船測量數據、模型試驗結果歸納出船舶在冰區航行阻力的經驗公式，將冰區船體阻力分為水阻力、破冰阻力和與速度有關的阻力，Lindqvist公式較為全面地考慮了船舶破冰總阻力的各種影響因素。Riska[2]基于一系列波羅的海不同船型的實船試驗數據，舍棄了冰參數的影響，得到了冰阻力經驗公式的簡單形式。

在冰材料力學性質及本構關系方面，部分學者基于海冰的物理性質及力學特性建立了冰材料的本構模型。但由于極地地區冰材料的復雜性，當前國內外對極地冰材料的本構模型研究尚未形成統一認識。Gagnon 等人[3]提出了基于可壓碎的泡沫材料模型，通過定義兩條屈服應力與體積應變曲線，低應力曲線用于碎冰，高應力曲線用于固體冰層。雖然該模型能夠解決頂層冰層融化，冰層下層保持固體的問題，變形大多是不可恢復，也沒有考慮冰裂縫和損壞。Liu等人[4]提出了一種適用于海冰的與應變率無關的塑性材料模型，將“Tsai-Wu”屈服面和相關流動規則結合起來描述冰山的本構行為，并在模型中考慮了冰山的溫度分布以及討論了應變率的影響，通過LS-Dyna中的用戶自定義程序，提出了基于有效塑性應變和靜水壓力的失效準則，用于實現裂紋萌生和損傷演化。Kim 和Daley 等人[5]進行了錐形冰的壓縮試驗，同時使用LS-Dyna中的可壓碎泡沫模型（MAT 63），改進并應用了相關材料特性，對冰進行了相應的數值模擬。其中，為了模擬在冰中實驗中經常觀察到的鋸齒荷載位移模式，增加了最大主壓力失效準則。Zong[6]通過改進可壓縮的泡沫模型來模擬海冰破碎行為，獲得了與極地規則里較為相似的壓力面積關系曲線，但該模型對應變率變化不敏感，因此對模擬冰的擠壓行為的適用性需進一步研究，同時在定義拉伸和壓縮相關曲線中應用了相同的應力-應變關系，并不能模擬冰的彎曲行為。Daiyan 和Sand[7]在LS-Dyna 中利用粘聚單元法（CEM）開發了海冰與海洋結構相互作用模型，冰層在結構連續相互作用下，相鄰的海冰粘性單元失效并且裂縫沿著粘性表面傳播，附著在失效粘性單元上的大塊單元從冰層落下以模擬海冰的破碎行為。Lu 等人[8]研究了冰彎曲模型中的單元侵蝕法（EEM）、黏聚單元法（CEM）、離散單元法（DEM）和擴展有限單元法（XFEM）等數值方法，并將這些數值方法用來模擬冰錐與錐形結構的相互作用。通常，在單元侵蝕法中，通過設定失效標準以產生彎曲裂紋；對于黏聚單元法，粘性元素被插入塊冰的單元間界面；離散單元法和擴展有限元法也利用黏聚單元進行裂紋萌生和擴展。Ince等人[9]基于相關文獻中對冰材料的測試數據以及實驗測試結果，提出了一種用于冰材料的本構方程，考慮到了應變率、鹽度和溫度對海冰力學特性的影響，根據臨界應變率來反映海冰的韌性和脆性行為。Lau[10]提出了一種用于模擬船冰相互作用的離散單元法，該模型中假定冰為各向同性彈脆性材料，冰失效基于Mohr-Coulomb 破壞準則和張力截斷值，能夠模擬冰沿單元間網格線斷裂，但不能模擬冰的彎曲失效。

近年來，冰阻力預報數值模擬方法的研究隨著計算機發展水平和應用程度的提高而越來越受到青睞，國內外學者在使用限元方法、離散元方法對破冰阻力的數值模擬方面具有了一定的研究基礎。Su[11]采用離散元方法對船舶-平整冰相互作用過程進行了數值研究，計算了在船體不同位置處的冰載荷。蔡柯[12]采用離散元法對船舶在平整冰中的航行過程進行數值模擬，探討了航速和冰厚對船體線載荷、局部冰壓力和總冰阻力的影響。Leira[13]等采用實船實驗方法，通過在某海岸巡邏艇船艏安裝的力學傳感器，研究了船舶在破冰航行時的船艏鋼結構應力情況，并通過有限元手段進行了數值計算對比。Zhou[14]等建立了船模與冰層作用的數值模型，模擬破冰過程中動態冰荷載，并與實驗結果進行了對比。何菲菲[15]利用Dytran 軟件對破冰船沖撞冰層過程進行數值仿真，分析了船舶在不同速度下的冰阻力情況。滕曼葛[16]利用LS-Dyna 軟件對破冰船船艏撞擊冰層過程進行了數值模擬，采用彈性支座代替浮力，分析了不同冰層厚度、海冰彈性模量、破冰船航速和艏部形式對冰載荷的影響。任奕舟[17]基于泡沫材料模型[18]模擬冰材料，采用LS-Dyna 對連續破冰過程進行了數值模擬，得到了不同船艏形式、冰層厚度下的冰載荷及破冰阻力，但在數值模擬中忽略了浮力的影響。

本文基于帶有塑性應變失效準則的彈性斷裂失效模型建立平整冰有限元模型，采用LS-Dyna 流固耦合方法對船舶在平整冰條件下航行的冰載荷開展數值模擬，選取船舶航速和平整冰厚度作為敏感性參數，分析了冰層破壞模式、參數變化對冰載荷及破冰阻力的影響。

1 LS-Dyna顯示時間積分算法及ALE算法

根據動力學問題的有限元方法，結構動力學方程經離散化變為

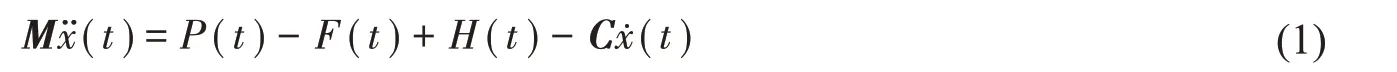
式中：M 為結構質量矩陣，x(t)為節點的加速度向量，P(t)為外力載荷向量，F(t)為內力向量，H(t)為沙漏阻力向量，C為阻尼矩陣，x(t)為節點的速度向量。

LS-Dyna采用顯示中心差分方法求解離散化后的動力方程，基本推導公式如下：

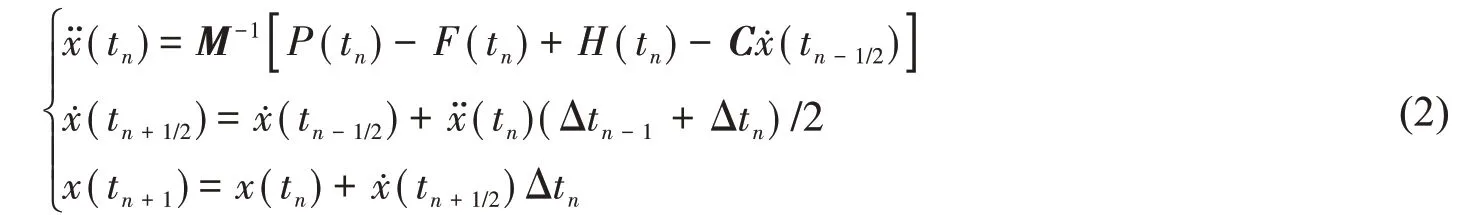
式中：tn-1/2=(tn+ tn-1)/2，tn+1/2=(tn+ tn+1)/2，Δtn-1= tn- tn-1，Δtn= tn+1- tn，x(tn)為tn時刻的節點加速度向量，x(tn+1/2)為tn+1/2時刻的節點速度向量，x(tn+1)為tn時刻的節點位置坐標向量。

利用LS-Dyna軟件研究“船-浮冰-水”流固耦合問題時，通常采用ALE方法（即Arbitrary Lagrange-Euler），該方法將Lagrange 和Euler 方法進行結合，ALE 方法突破了固體大變形數值計算的難題，目前已經成為分析大變形問題的重要數值方法。

任意物理量f在ALE描述下對時間的導數由兩部分組成：

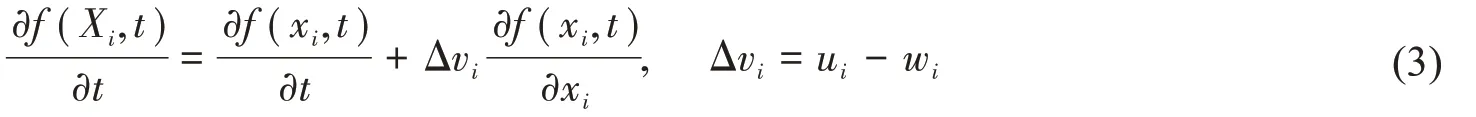
（3）式中，Xi和xi分別為拉格朗日坐標和歐拉坐標，Δvi為相對速度，ui和wi分別為流體質點速度和參考坐標系下的網格速度。通過上式又可導出ALE 描述下的流體連續性方程及動量方程，由質量守恒原理用流體密度ρ描述（3）式中的物理量f可得：

（4）式即為流體連續性方程，對于不可壓縮流體，可簡化為

結合牛頓第二定律對流體微元運動情況進行分析，可導出流體單元本構方程：

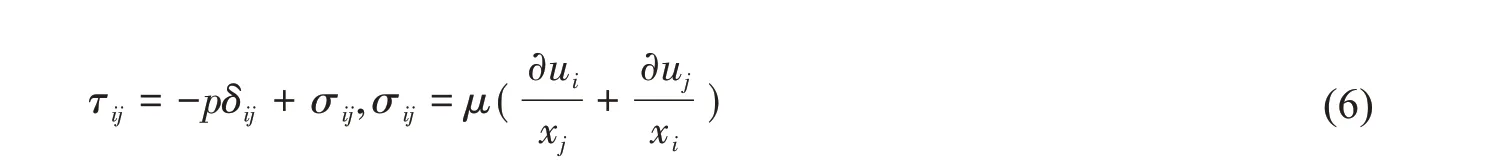
式中：p為流場壓強，μ為粘性系數，τij為應力張量，δij為Kronecker δ函數。

根據流體單元上壓力、質量力、粘性力以及慣性力相平衡的條件可以推出

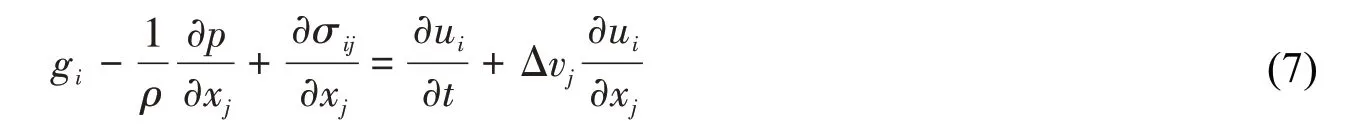
將（6）式中的σij代入（7）式中可得ALE描述下的流體動量方程：

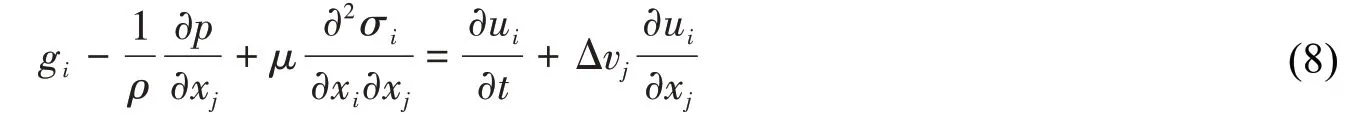
LS-Dyna采用罰函數約束的方法來實現流固耦合，程序將自動追蹤拉格朗日節點（船體結構和浮冰）和歐拉流體（水和空氣）位置間的相對位移，檢查每個從節點對主物質表面的貫穿，若發生從節點對主物質表面的貫穿，界面力fs就會分布到歐拉流體的節點上，耦合界面會在ALE的每個輸運載荷步中進行重構，對未出現該情況的則不進行任何操作。

界面力大小受貫穿點的相對位置影響，滿足如下關系式

式中：δi為穿透量，ki為接觸剛度因子。

2 船舶破冰阻力數值計算

2.1 有限元模型及材料參數

計算模型的水域和空氣域長寬為200 m×100 m，水深12 m，空氣域高度8 m，建模時將二者處理為共面，劃分網格時將兩種材料處理為共節點，水和空氣均采用Null 材料模型，狀態方程分別采用GRUNISEN 和LINEAR_POLYNOMIAL 描述，流場外邊界全部采用無反射邊界條件*BOUND‐ARY_NON_REFLECTING。流體域實體單元采用變間距網格劃分，網格在z方向上以自由液面處為起始面向兩端漸變式增大，流體域網格總數為260 000個。

冰體材料[19]采用*MAT_ISOTROPIC_ELASTIC_FAILURE，該材料是帶有塑性應變失效準則的彈性斷裂失效模型，當有效塑性應變達到失效應變或當壓力達到失效截斷壓力時，單元失去承載應力的能力，偏應力變為零，即材料表現為流體狀態。相關材料參數和船舶主尺度參數如表1所示。

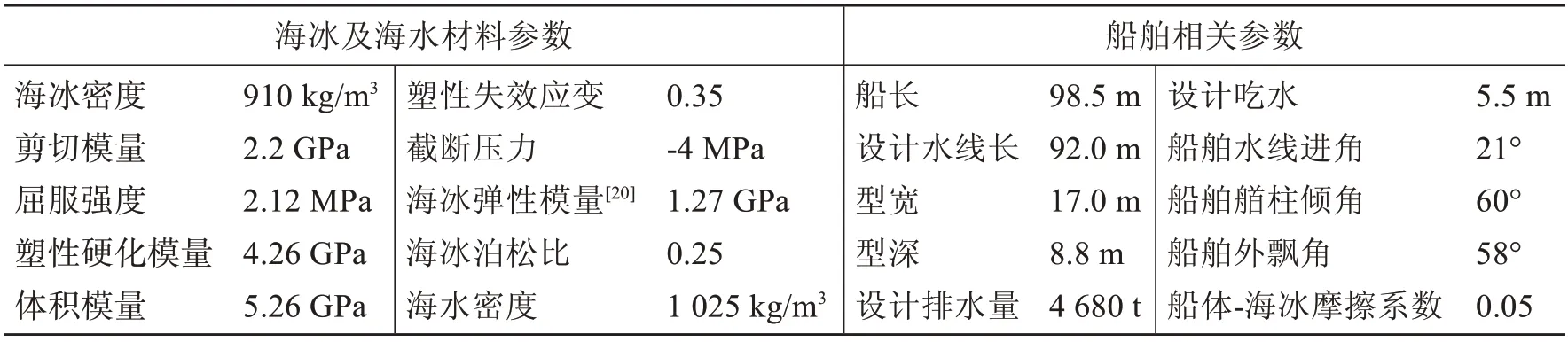
表1 相關材料參數和船舶主尺度參數Tab.1 The material parameters of ice and main parameters of the ship

船體所有節點僅在z 方向上的位移受約束，在x 方向上以恒定航速運動；平整冰長寬為180 m×180 m（長度約為船長2 倍，寬度約為船寬5 倍），其各邊與流體各對應邊界的間距均為10 m，平整冰與水面的初始間距為0.01 m，xy 平面內網格尺寸為0.5 m×0.5 m，z 方向單元層數為2 層。為研究船舶在進入冰層、連續破冰、駛出冰層過程中的破冰載荷及阻力情況，采用LS-Dyna ALE 流固耦合方法對上述大跨度破冰過程進行數值仿真，設定船速5 kn，軟件模擬時間為77.8 s，船舶破冰距離約為200 m。平整冰邊界條件設置及船舶-平整冰環境有限元模型如圖1所示。

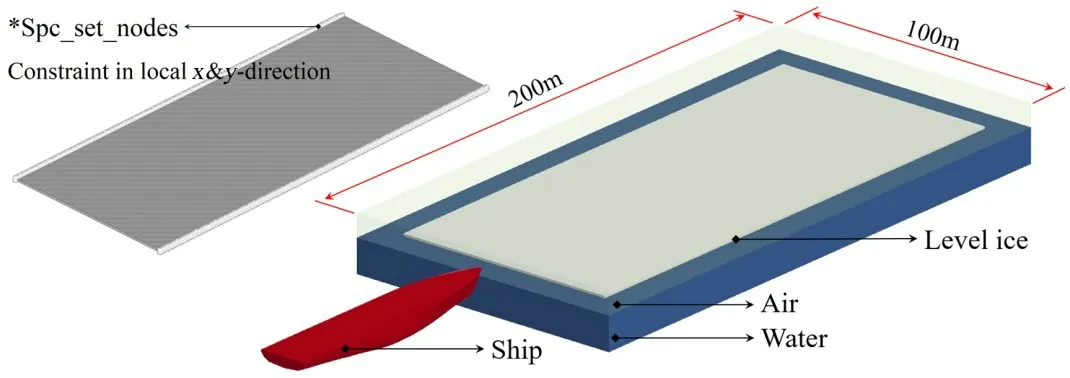
圖1 船舶-平整冰環境有限元模型Fig.1 FEM model of geophysical prospecting vessel-leveling ice environment

2.2 計算結果及經驗公式對比分析

隨機選取平整冰內4 個單元節點作為監測點，船舶航行的前4.5 s 內未接觸平整冰，在t = 4.5 s 時刻的平整冰監測點位置及穩定浮態如圖2所示，在0～4.5 s時間內的監測點z方向加速度時歷曲線如圖3 所示。從圖中可以看出，在平整冰向下運動過程中，監測點z 方向加速度在初始時刻經過劇烈變化后在0 值附近振蕩。這表明冰層經歷短暫動平衡過程后基本到達平衡位置，具有穩定浮態，設置浮冰-水面初始間距對浮力的方法有效。

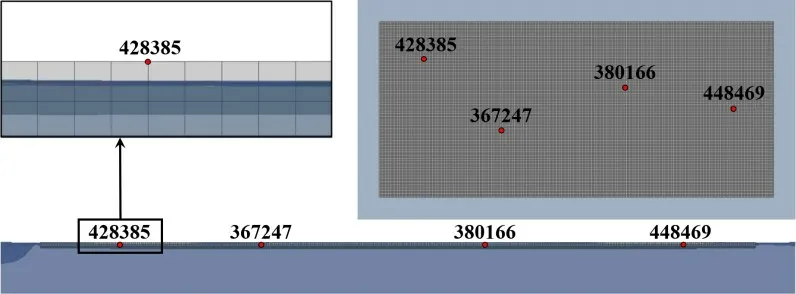
圖2 監測點位置及穩定浮態示意圖 Fig.2 Monitoring point position and stable floating state diagram

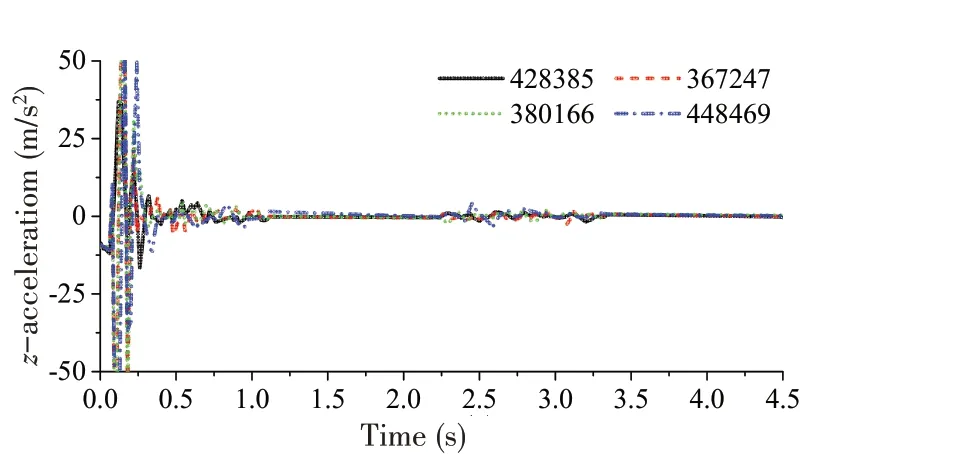
圖3 z方向加速度時歷曲線Fig.3 z-direction acceleration-time history curve

通常情況下，海冰與結構物相互作用時，主要有以下四種破壞模式[21]：

（1）擠壓破壞：冰層被作用區域因受擠壓而逐漸破碎；

（2）壓曲破壞：冰層由于受壓在結構物前隆起隨后發生破壞；

（3）縱向剪切破壞：冰層受到剪應力達到強度極限時產生與運動方向一致的裂縫；

（4）彎曲破壞：冰層沿斜面結構運動，隨后受彎最終發生彎曲破壞。

典型時刻下的冰層破壞模式如圖4所示，該圖視角為仰視和側視，冰層典型破壞模式如局部放大圖所示。平整冰在帶傾角的船艏和浮力的作用下，處于一種復雜的三維受力狀態，準確地描述自然環境下的冰裂紋生成及擴展方式還具有一定難度，況且有限元網格劃分方式和精細程度同樣對其有影響。因此，冰層破壞模式分析僅給出基于有限元模擬結果的現象描述，不作具體理論分析。總體而言，冰層破壞模式、冰裂紋生長過程及碎冰脫落、碎冰翻轉、碎冰滑動清除等現象比較真實地反映了船舶在平整冰環境下的破冰過程。從模擬結果來看，平整冰在船舶連續破冰過程中表現出的破壞模式基本符合文獻[21]描述。

x、y、z 方向上的冰載荷-時間歷程曲線如圖5 所示，可以看出船舶在x 方向和z 方向受到冰載荷的幅值分布較為相似，y方向冰載荷振蕩范圍基本處于x和y方向冰載荷時歷曲線包絡線內，各方向上的冰載荷在時域上均存在一定的周期性，以x方向上的冰載荷為例，周期性波形圖如圖6所示，在5～76 s時間范圍內（航程約為兩倍船長的距離），可以很明顯地觀察到3個振蕩形式相似的完整波形，對該時間段內的冰載荷進行數據統計得到船舶的破冰阻力為3.79 MN。

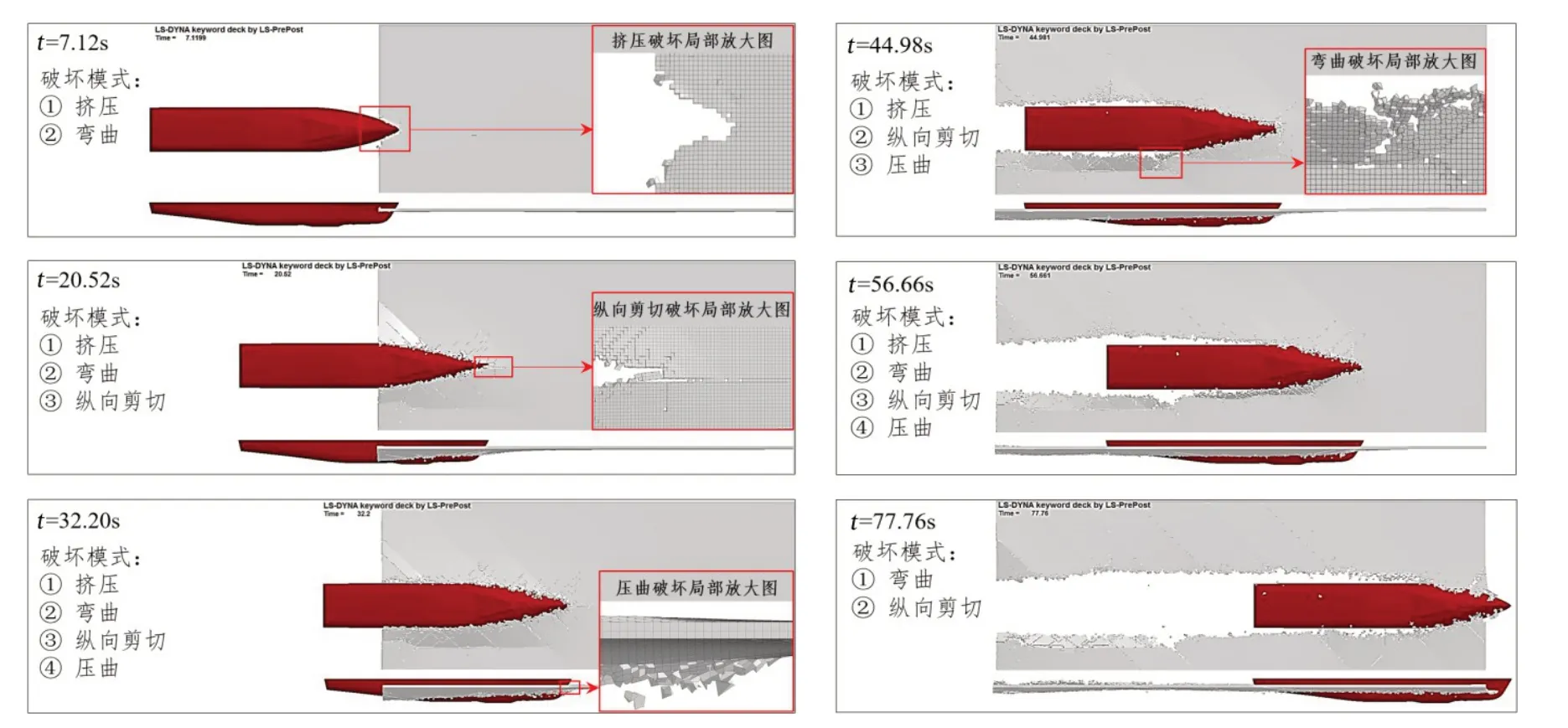
圖4 典型時刻下的冰層破壞模式Fig.4 Ice failure modes at typical times

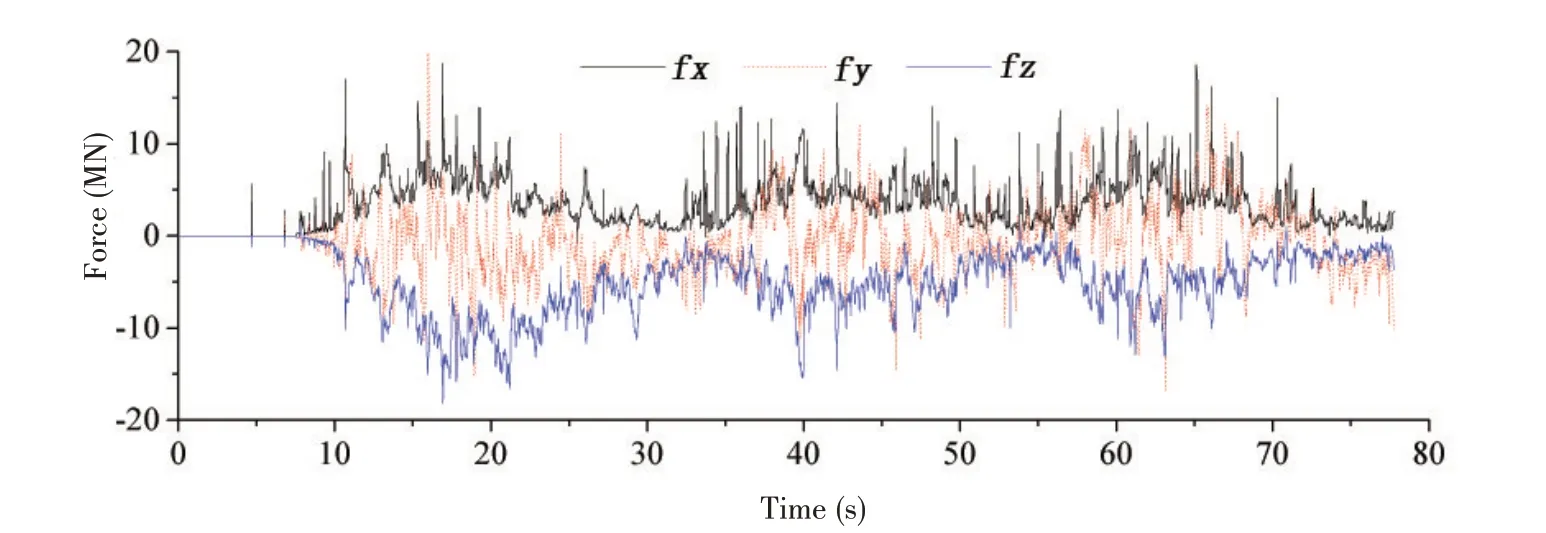
圖5 x、y、z方向上的冰載荷-時間歷程曲線Fig.5 Ice loads-time history curve in x,y and z directions

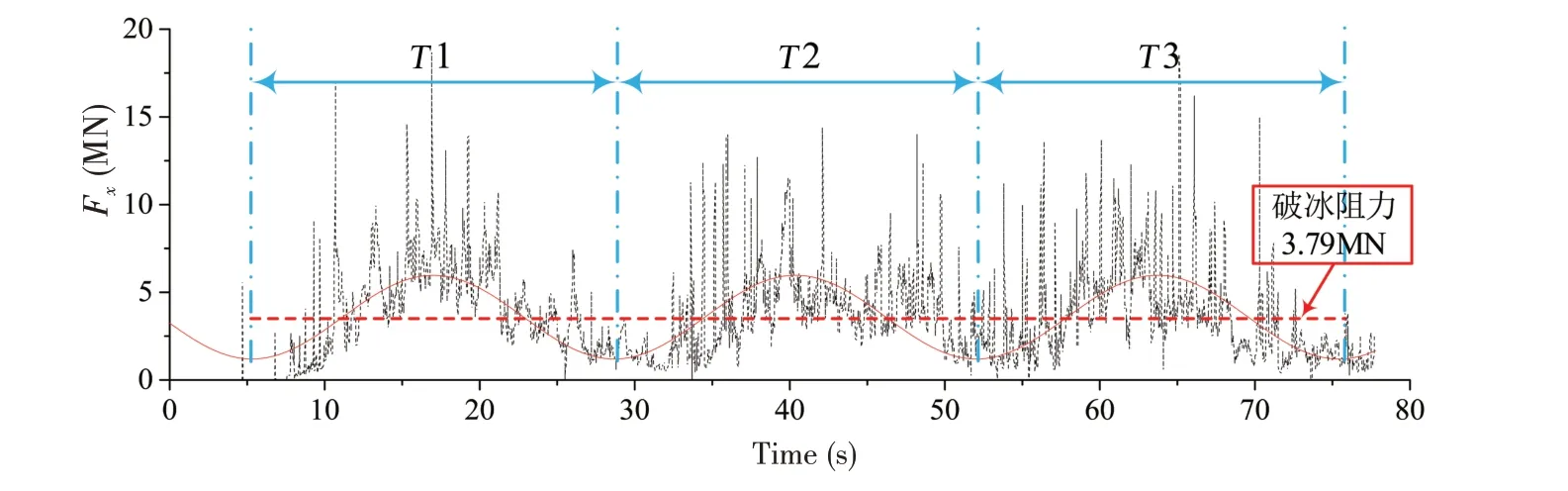
圖6 x方向上的冰載荷周期性波形圖Fig.6 Waveform of ice loads in x directions

將數值模擬結果的破冰阻力與Lindqvist經驗公式[1]進行對比，該公式將破冰阻力R具體分為破碎阻力Rc、彎曲阻力Rb和依賴于速度的浸深阻力Rs（也稱為壓沉阻力，可細分為摩擦阻力和勢能損失），各成分冰阻力計算公式如下：

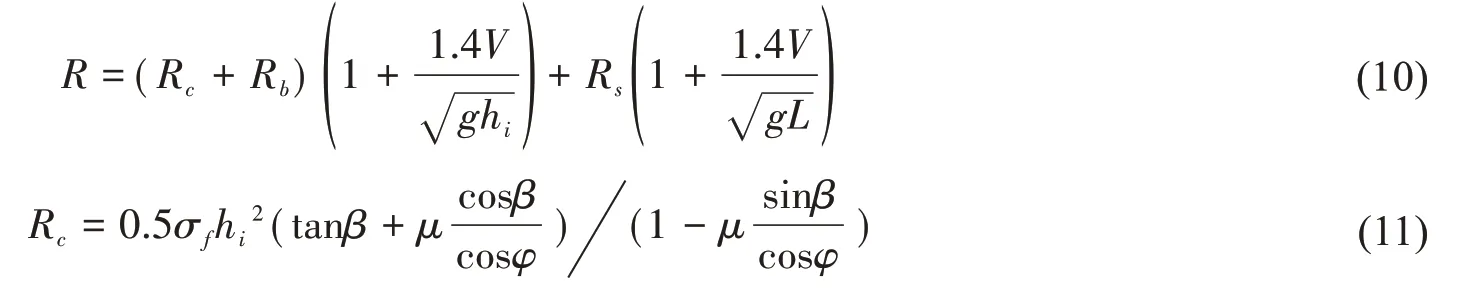
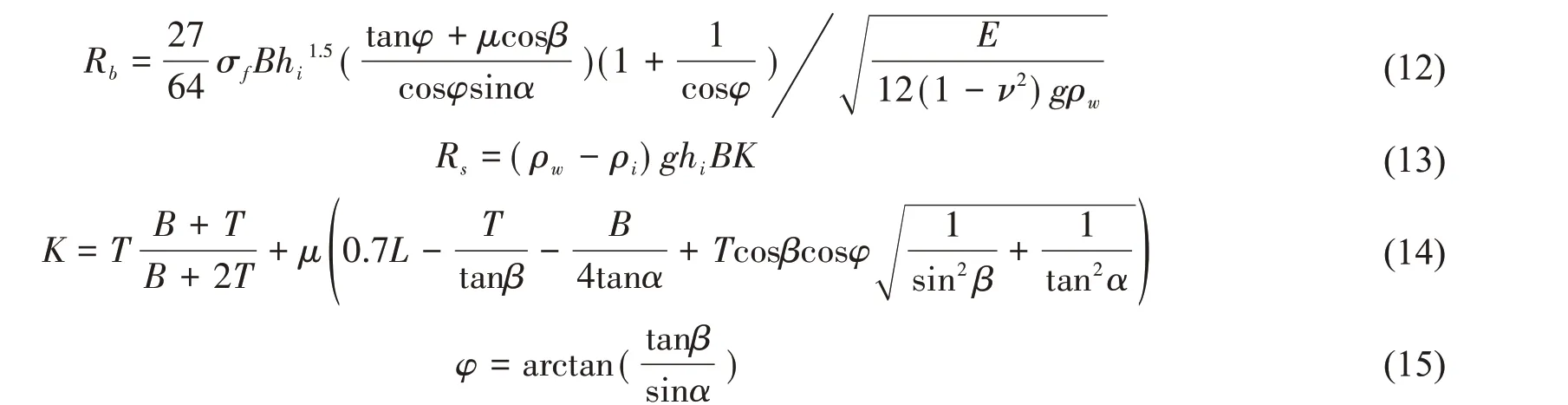
（11）-（12）式中的σf為海冰彎曲強度，一般認為海冰彎曲強度隨總孔隙率增加而減小。Timco[22]整理了前人所做2 500個淡水冰和海冰的抗彎強度實驗數據，得出第一年海冰的彎曲強度σf計算公式為

式中，Vb（‰）為鹽水體積，當溫度在-22.9℃～0.5℃時，Frankenstein[23]給出鹽水體積公式為

式中，Si（‰）為海冰鹽度（包含在單位質量海冰內的鹽的質量分數），T 為冰的溫度（℃）。海冰鹽度通常隨冰厚度變化而變化，在結冰期中，鹽會沿著厚度方向向下移動，所以在許多情況下，鹽分布的平均值被近似用來表示鹽度。Kovacs[24]給出冰厚與鹽度關系表達式為

根據公式（16）-（18）計算可得溫度為-20℃時，1 m厚的海冰彎曲強度σf=0.824 MPa。

將海冰彎曲強度、相關海冰參數和船舶參數代入到（10）～（15）式中計算得到總破冰阻力為R=4.01 MN，數值模擬得到的船舶破冰平均阻力3.79 MN 與經驗值為同一量級，誤差約為-5.5%，在可接受范圍之內。因此，本文采用流固耦合方法對船舶破冰阻力預報及參數敏感性開展數值模擬研究具有一定的可靠性。

3 船舶破冰阻力參數敏感性分析

為分析船舶航速和平整冰厚度對船舶破冰阻力的影響，開展了破冰阻力航速敏感性及冰層厚度敏感性研究。船舶破冰阻力參數敏感性工況如表2 所示，共計10 個工況，船舶破冰距離均為200 m。不同敏感新參數下的船舶破冰情況（船舶完全進入冰層時刻）如圖7 所示，從俯視視角可以看出平整冰發生了明顯的斷裂和破碎，從側視視角可以看出破碎的冰塊下沉隨后沿貼合船體表面滑動的現象，冰層在不同敏感性參數下的破碎程度和裂紋生成均有一定的差異。該過程影響因素較多，隨船速和冰層厚度的增加未表現出明顯的規律性，具有較強的隨機性。

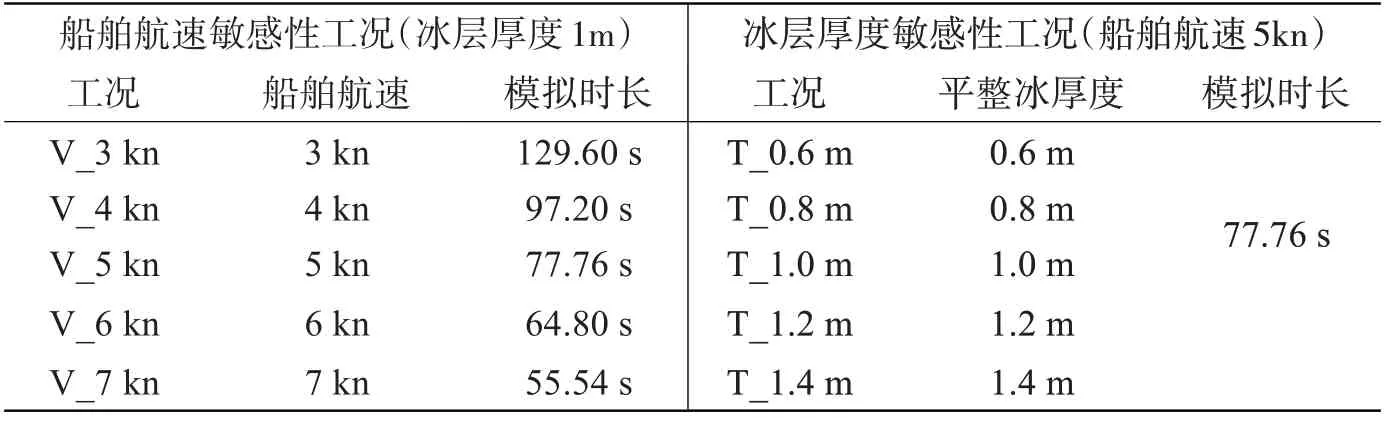
表2 破冰阻力參數敏感性工況Tab.2 Cases of sensitivity parameters of ice-breaking resistance

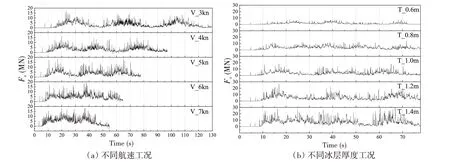
圖8 x方向冰載荷-時間歷程曲線Fig.8 Time history curve of ice loads in x direction

x 方向冰載荷-時間歷程曲線如圖8 所示，可以看出時域上的冰載荷振蕩呈現較明顯的周期性。不同敏感性參數下的時歷曲線上出現第一個非零值后，均出現了一小段冰載荷卸載的情況，主要原因是船舶剛接觸冰層產生擠壓破壞致使冰層應力集中，導致大量冰體單元失效刪除。因此，數值模擬的數據統計時間起點取為冰載荷出現第二個非零值時刻，統計結束點取為船艏即將駛出冰層邊界時刻。

對冰載荷進行數據統計可得到破冰阻力，并將數值模擬結果與Lindqvist 經驗值對比，破冰阻力、統計時間范圍及Lindqvist 經驗值如表3 所示。不同航速及冰厚條件下的破冰阻力與Lindqvist 經驗值誤差分別在-7.5%～13.1%和-10.8%～19.4%范圍內。考慮到海冰的鹽度、溫度、彈性模量、彎曲強度等材料參數受環境因素影響較大，經驗公式計算值僅作為數值模擬的參考依據。總體而言，數值模擬結果與經驗值吻合較好。

不同敏感性參數下的破冰阻力數值模擬結果與經驗值對比如圖9所示，從圖中可以看出，破冰阻力的數值預報結果及Lindqvist 經驗值都隨船速和冰厚的提高均呈線性遞增的趨勢，不同航速工況的數值模擬結果在低航速時與經驗值誤差相對較小，不同冰厚工況的數值模擬結果擬合曲線與經驗值吻合良好。

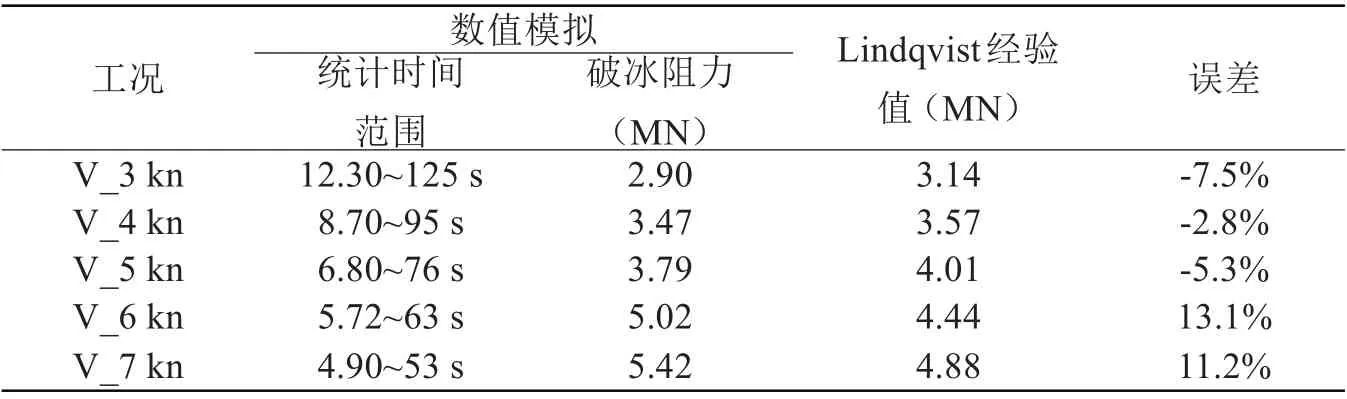
表3 破冰阻力及經驗值統計數據Tab.3 Statistical data of ice-breaking resistance and empirical value on ice layer failure model

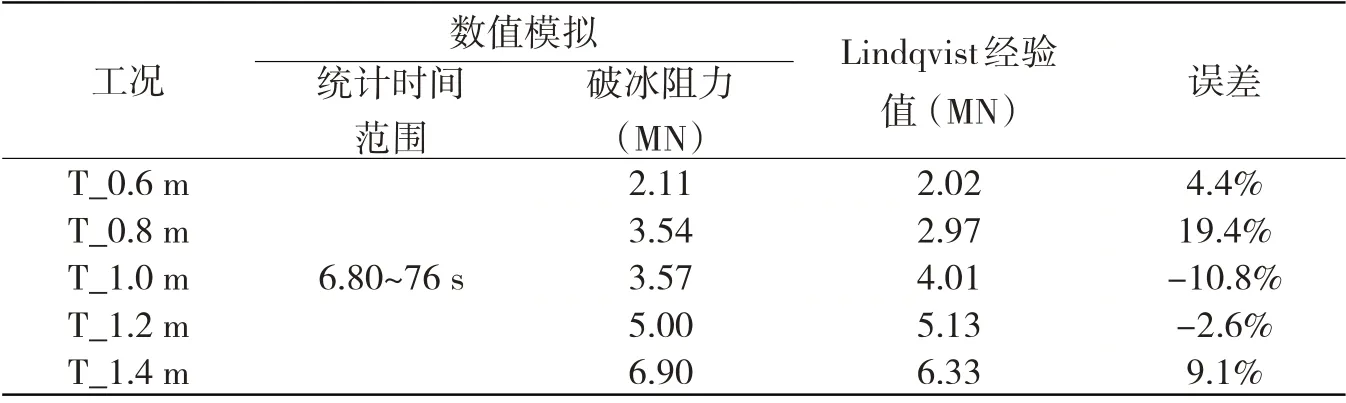
續表3

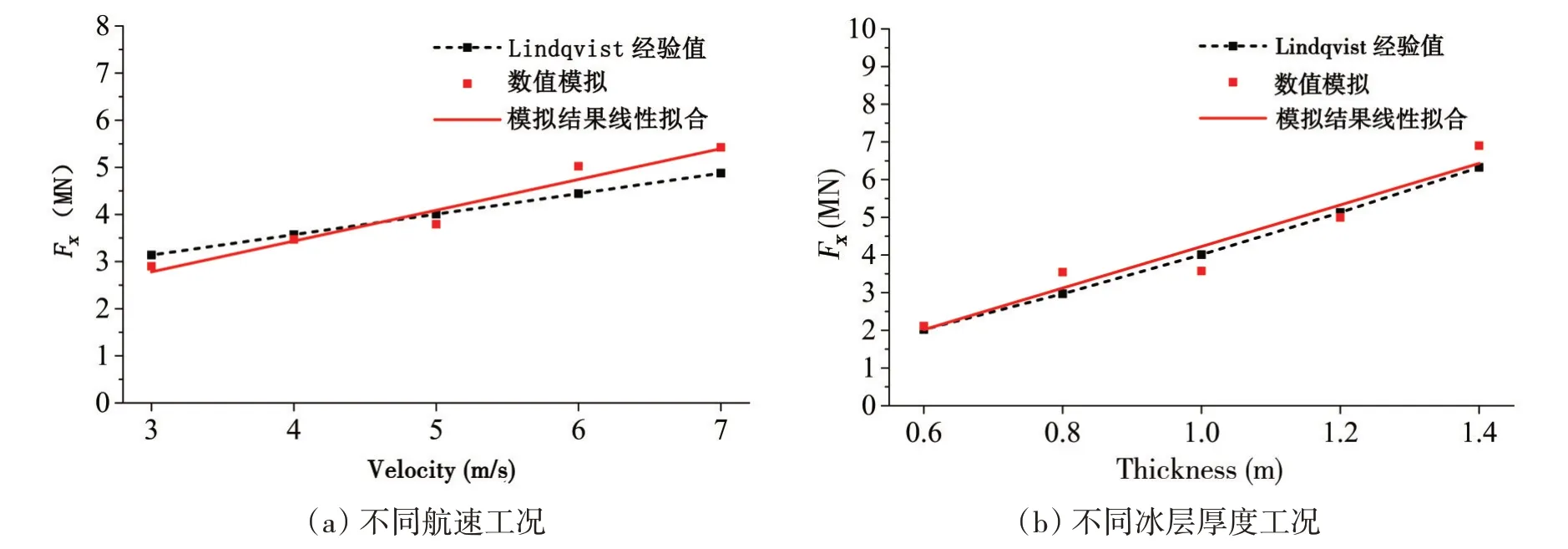
圖9 破冰阻力的數值模擬結果與經驗值對比Fig.9 Comparison of ice-breaking resistance between numerical simulation and empirical values

4 結 論

本文基于冰材料為帶有塑性應變失效準則的彈性斷裂失效模型，采用LS-Dyna流固耦合方法對船舶在平整冰條件下航行的破冰阻力開展了數值模擬，選取航速和平整冰厚度作為敏感性參數，分析了參數變化對破冰阻力的影響，并將模擬結果與Lindqvist經驗公式計算值進行了對比，得出如下結論：

（1）船舶在x 和z 方向受到的冰載荷的幅值分布較為相似，y 方向冰載荷振蕩范圍基本處于x 和z方向冰載荷時歷曲線包絡線內，各方向上的冰載荷在時域上均存在一定的周期性，在航程約為兩倍船長的距離內，冰載荷時歷曲線上存在3個規律性較強的重復波形。

（2）數值模擬平整冰的破壞模式基本上符合文獻對擠壓破壞、壓曲破壞、縱向剪切破壞、彎曲破壞的描述。上述破壞模式通常不會單獨出現，冰層在船艏擠壓和浮力作用下，通常以多種破壞模式的混合方式同時出現。

（3）船舶在平整冰環境下的破冰阻力隨航速和冰厚的提高基本呈線性增加的趨勢，不同航速及冰厚條件下的破冰阻力與Lindqvist 經驗值誤差分別在-7.5%～13.1%和-10.8%～19.4%范圍內，采用LS-Dyna流固耦合方法對船舶破冰阻力進行預報具有較高精度。