基于凸顯本質下的小學數學認識方程教學策略研究

王桂瓊　譚德君

摘 要：方程的學習是學生突破算術思維，形成代數思維的重要過程。新課標明確指出教師的教學應揭示知識的數學實質及其體現的數學思想，幫助學生理清相關知識之間的區別和聯系。文章通過查閱相關文獻，走進學生的世界，提出淡化概念形式，立足學生需要，理清算式與等式關系的教學設計理念，呈現凸顯本質下的小學數學認識方程教學策略。

關鍵詞：凸顯本質;小學數學;認識方程;教學策略

方程的學習是學生發展代數思維的關鍵一步，形成模型思想的必要經歷，養成數學核心素養的重要途徑。新課標指出課程的設計要有利于激發學生的學習興趣，引發數學思考，體現數學的實質，使學生體驗從實際背景中抽象出數學問題、構建數學模型、尋求結果、解決問題的過程。正如史寧中所說，只有親身經歷數學化活動，才能真正形成數學核心素養。反觀現狀，學生熟記于心的是方程概念的外殼，而非方程的本質，存在“被逼”使用方程的學生。故下文借鑒俞正強老師執教的《認識方程》一課，就如何在小學數學教學活動中凸顯方程的本質，讓學生真正意義上理解方程，感悟模型思想，建立代數思維，習得數學核心素養展開論述。

一、 教學設計理念

（一） 淡化概念形式，把握方程本質

陳重穆先生曾說，“含有未知數的等式叫做方程”這樣的定義要淡化，不要記，無需背，要淡化，更不要考。關鍵是要理解方程的本質及它的價值和意義。實際上，通過式子是否含有字母，是否為等式兩點來判斷方程的方法成為了教學的重點，這顯然忽視了方程的本質。

人們也不禁會產生疑問，“x=1”中既含有字母x，又是一個等式，那它是方程嗎？細細推敲，這個式子中的x是一個為“1”的已知量。因此，從形式上看，“x=1”是方程，但究其本質，“x=1”是一個值，不是方程。故“含有字母的等式就是方程”這個概念是錯誤的傳承，方程是含有字母的等式，而含有字母的等式并不都是方程。正如張奠宙先生所總結那般：方程是為了尋求未知數，在未知數和已知數之間建立起來的等式關系。凸顯出了方程的本質，即方程是一種關系，表現方式是等式，溝通已知和未知的橋梁，最終目的是使得我們可以借助這層關系求出未知數。因此在教學中要把握方程的本質，深入探究未知數的內涵，體會方程蘊含的數學思想，構建含有數學味的數學課堂。

（二） 立足學生需求，提升數學素養

走進學生的生活，了解學生的想法后，我們會發現大部分學生認為很多應用題可用算式解答，根本無需增添解設、寫等量關系的“麻煩”。

當學生未掌握方程的本質時，自會產生方程無用論。因此，教學中要讓學生在探索中摸清“等量”的內涵，學會找等量，并利用等式建立量與量之間的聯系，列方程求解。深刻體會方程的應用能夠使復雜的問題簡單化，逆向思考的問題直觀化。感知方程是解決問題的新的便捷之路，從而愛上和使用方程解題。

數學建模，即對現實問題進行抽象，用數學語言表達問題，用數學知識與方法建構模型解決問題的過程，是普通高中數學學科核心素養的一項重要指標。而方程的學習正是數學建模不可缺少的部分。如果把數學建模比作一棵大樹，那么方程的學習要成為這棵大樹上的一片葉子，或是一顆擁有無限生機、能夠開枝散葉的嫩芽，都取決于我們是否將方程的本質傳授給學生，給其發展所需，讓其不斷有新的生成。

（三） 理清知識關系，發展批判思維

1. 算式和等式體現的思維特征不同

算式體現的是思維的可逆性，如由90×8=720，可得720÷90=8，以及被減數=減數+差等等都是互逆性的體現。而等式卻表達出思維的守恒性特征，體現的是代數還原和對消的本質。等式的左右兩邊應該是同時做同樣的變化，如已知x+8=60，那么可以轉化為x+8-8=60-8，最后得出x=52。

2. 算式和等式運用的思維方式不同

解決問題時，算式運用的是算術方法，等式利用的是代數方法，它們解決問題的思路往往是相反的，但結果是相等的。

例：小紅的媽媽今年32歲，比小明的3倍還多5歲，求小紅的年齡。

算術思維：根據下一步所需列出式子：（32-5）÷3，得出小紅的年齡是9歲。

代數思維：設小紅的年齡為x歲，列出方程3x+5=32，從而解得x=9。

上述式子中，我們可以直觀感受到算式和等式所利用的思維方式的不同，但最終都歸結為一個結果。正如張奠宙先生所比喻，答案如果是對岸的一塊寶石，那么算術方法是摸著石頭過河，從我們知道的岸邊開始，一步一步摸索著接近對岸的未知目標;而代數方法好像是將一根帶鉤的繩子甩過河，拴住對岸的未知數（建立了一種關系），然后利用這根繩子（關系）慢慢的拉過來，最終獲得了寶石。

3. 算式和等式適用的題目難度不同

問題較為簡單，事情的主角只有一個時，運用算式解題更為便捷快速。

例1：從甲地到乙地，每小時行駛80千米，5小時到達，甲地到乙地距離有多少千米？

這時候強調的是開車，并且只有一個主角在開，因此只需要根據速度×時間=路程進行列式80×5=400（千米）得出結果。

但解決較復雜的應用題時，列出等式往往能使復雜問題更為直觀、簡單解決。

例2：從甲地到乙地，貨車每小時行80千米，5小時到達。客車每小時行駛100千米，問客車幾小時能夠到達乙地？

這時候題目中有客車、貨車兩個主角，但他們之間有等量，即最后行駛的路程都是甲乙兩地的距離。因此我們設客車x小時能夠到達乙地，得到等式：80×5=100x，從而能夠快速的得到x=4。

4. 算式和等式中“=”存在的意義不同

還必須理解算式和等式中的等號含義的不同，在算式中“=”表示的是一個結果，如上體中80×5=400，等號就是表示得出400這個結果;而等式中的“=”表示的是兩邊式子是等量的，作為連接符而存在。

二、 認識方程教學策略

（一） 在具體情境中建立等量的概念

建立等量的概念，是學生在認識方程必要前提。認識方程時對等量有正確的理解，就相當于建房子時已經打好了地基，可以在上面無限發揮，建立各種各樣的房子。因此，需要明白等量不是一個特定的量，等量蘊含在具體的情境中，要讓學生愛具體的情境中感悟，也是切合新課標的要求，要結合簡單的實際情境，了解等量關系。

例：6個蘋果重3千克體現的是總量;一個蘋果重3千克講體現的是每份量，這兩句話中間并不存在等量。但如果它們出現在某一情境中，如6個蘋果重3千克，8個蘋果重4千克，那么這時就存在等量，即1個蘋果的重量是6個蘋果和8個蘋果這兩個主角間的等量。

因此，引導學生理解等量是發生在含有兩個主角的情境之中是建立等量這個概念的關鍵所在。教師可以設置幾個具體情境，讓學生在操作中感悟各種情境中，兩個主角間的等量所在。

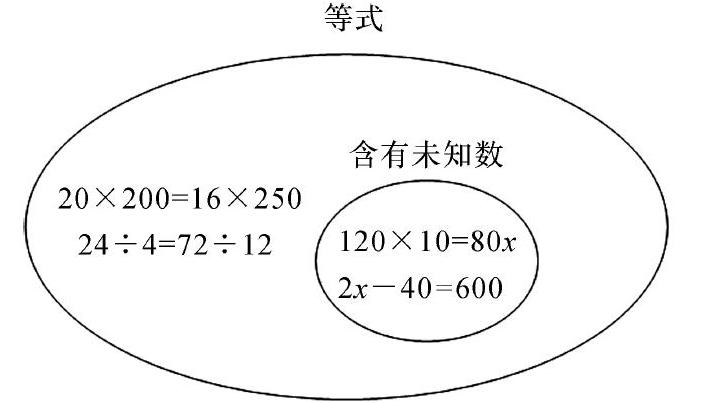
例1：甲工程隊每天鋪設20米，需要200天完成，乙工程隊每天16米，需250天完成。

引導學生觀察，發現甲工程隊、乙工程隊是故事中的兩個主角，得出鋪設的總長是等量。

例2：做衣服，若做4件衣服，需要24粒扣子;若做12件衣服，則需要72粒扣子。

引發學生觀察思考，明白做4件衣服和做12件衣服是故事中的主角，體會每件衣服所需要的扣子數便是等量。

（二） 在等量理解中建立等式

史寧中曾說，等式兩邊講兩個故事，這兩個故事的量相等。其實這就是等量的意義，等量的理解是建立等式的基本條件。學生對等量理解的基礎上，進一步引導學生列出相應的等式，讓學生運用自如，簡便有效，才能激發學生學習數學的熱情，感悟方程的價值。

如設計含有未知數的問題，指導學生在尋找等量后，利用“=”連接等量，如此一來，學生得出等式便是水到渠成的事。

例3：從甲地到乙地，客車每小時行使120千米，需要10小時走完;貨車每小時行使80千米，需要x小時走完。

例4：甲每天采摘蘋果600個，乙每天采摘x個，已知乙的2倍少40個，正好與甲相等。

在對等量的理解中，學生可以毫無障礙的找出例3和例4中的等量分別是甲地到乙地的距離和甲采摘的蘋果個數，從而利用連接符“=”，得出120×10=80x，2x-40=600。讓學生在理解等量的基礎上體驗等式的建立，明白等式的到來時不費吹灰之力時，自然而然有震撼的感覺，發出歡喜的聲音。

（三） 在等式理解中感悟方程

學生經歷等量的理解，等式的建立，通過對比上述例題中的等式：

通過比較，發現等式中的特殊形式：有些等式含有未知數。由此教師再次引導學生體會將未知當成已知寫成含有未知數的等式的方便快捷，歸納總結出：像120×10=80x，2x-40=600……這樣，含有未知數的等式便是方程。從而了解方程的本質，認識方程，建構了一堂有生長力的課堂，即教師傳授知識的本質，滲透數學思維與思想方法，給學生留下迸發新知的“源泉”。

三、 結語

凸顯本質的方程教學，不僅讓學生認識了方程的“外表”，更關注學生的需要，讓學生體會算式到等式飛躍的必要性以及等量的確定、等式的建立、方程的實質。使得學生在學習中感悟方程的實用性，愛上有方程的數學，發生思維的轉變，有了方法的生成，提高運用能力，生長新的知識，發展數學核心素養。

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2]孔凡哲，史寧中.中國學生發展的數學核心素養概念界定及養成途徑[J].教育科學研究，2017（6）：5-11.

[3]宋乃慶，陳重穆.再談“淡化形式，注重實質”[J].數學教育學報，1996（2）：15-18.

[4]張奠宙.概念教學要融入中華文化，推陳出新——談小學數學里“方程”概念的表述[J].小學教學（數學版），2014：11-16.

[5]彭慧.高中數學核心素養之建模能力的培養[J].數學教學通訊，2017（6）：62-63.

作者簡介：王桂瓊，譚德君，福建省廈門市，集美大學教師教育學院。