一類分數階分段光滑系統的非線性振動特性

王 軍， 申永軍， 楊紹普， 溫少芳， 王美琪

(1.石家莊鐵道大學 機械工程學院，石家莊 050043； 2.石家莊鐵道大學 交通運輸學院，石家莊 050043)

近年來非線性科學研究發展迅速，其中的非光滑動力系統作為非線性動力系統的一部分，更是研究熱點之一。非光滑運動廣泛存在于諸多振動系統中，如車輛懸掛系統、緩沖器、振動篩、振動輸送機等由于間隙的存在，均存在非光滑動力學行為，會對系統的動態特性產生不良的影響，甚至給車輛或機器帶來嚴重的安全隱患。已有許多國內外學者投入到了非光滑動力學研究中，其中分段光滑系統的研究也取得了一些進展。衛曉娟等[1]分析了單自由度分段光滑系統由n-1周期運動經周期倍化分岔通向混沌的行為，接著對系統混沌運動的控制做出了研究。張正娣等[2]研究了非光滑Duffing振子隨慢變參數變化的不同平衡點和相應的分岔行為，揭示了該類非光滑系統中不同簇發振蕩的產生機理。張思進等[3]針對齒輪系統的分段線性模型，運用Melnikov理論研究了齒輪系統異宿軌道的全局分岔條件以及系統周期運動的穩定性。Li等[4]得到了分段光滑系統的次諧軌道的Melnikov函數。Huang等[5]得到了具有負剛度的受控分段光滑系統的頻率響應和穩定性條件，并研究了該系統出現的對稱破裂分岔和混沌運動。已有研究表明，選擇合適的系統參數可以對原有動力學系統的性能進行提升，比如可以避免振幅的跳躍、改變系統的分岔行為以提高系統工作的穩定性[6-9]。

對于黏彈性材料如車輛懸掛系統中的元器件磁流變阻尼器、油壓減震器等，若單純地考慮其彈性特性或阻尼特性而建立的模型并不能完全反映材料本質。和整數階相比，分數階模型能夠更好地描述材料的黏彈性，更能準確地描述一些物理變化過程和非線性特性。其實，整數階微積分僅是分數階的一個特例，是一種理想化的形式。因此，以分數階微積分模型來優化傳統的整數階模型會更加準確，更能反映系統的本構關系。相關研究也表明采用分數階微積分建立的模型更準確，更能描述實際系統的動態特性。如孫會來等[10]引入分數階導數建立了油氣懸架的模型，并通過數值及實驗驗證了分數階模型比整數階模型能更精確地描述油氣懸架的特性。Lewandowski等[11]采用分數階模型對黏彈性阻尼器進行了描述，通過理論分析了該類阻尼器的設計敏感性，并舉例進行了驗證。李占龍等[12]提出了基于FKV本構的黏彈性懸架分數階減振模型，并用數值方法得到了這種黏彈性懸架響應具有全局相關性和記憶性。吳杰等[13]以橡膠隔振器為研究對象，給出了隔振器的分數階動力學模型，并與傳統模型進行了對比分析，結果表明含有分數導數的模型能夠較好地預測橡膠隔振器的動態特性。

在振動力學方面，正是由于分數階模型表現出來的這些良好的特性，使得更多的學者致力于分數階模型的振動特性研究。Shen等[14-16]采用平均方法研究了不同分數階微分振子的動力學行為，發現分數階微分項不僅起線性阻尼的作用，還可以等效為線性剛度。Xu等[17]結合L-P方法和多尺度方法提出一種新的方法求解分數階Duffing振子的二階近似解，并采用蒙特卡洛方法分析了該系統的動力學特性。Chen等[18]采用隨機平均法對一個分數階微分振子的統計響應做出了研究，得到了一些統計指標如條件可靠性函數和條件概率密度函數等。Xiao等[19]采用諧波平衡法建立了分數階Vander Pol 振子周期解的近似表達式。對于求解一次近似解的多種分析方法來說，平均法是一種處理分段系統更為成熟、更為直觀的方法，故本文采用該方法對分數階和分段光滑系統進行研究。

但是目前對于分段光滑分數階系統的研究還比較少，而且多采用數值方法進行研究，在現有的文獻中，Wu等[20]采用數值方法研究了一個分數階分段線性系統，發現了不動點、周期運動和混沌運動等豐富的動力學行為，提出了基于分數階滑模控制的混沌同步控制策略。Lu[21]對含分數階的分段線性蔡氏電路的混沌行為進行了分析，發現奇次分數階蔡氏電路發生混沌的最小階次是2.7，非齊次分數階蔡氏電路發生混沌現象的最小階次為2.8。

通過以上文獻可以看出，現有研究多偏重于單獨的分段光滑系統或單獨含分數階微分項系統的動力學理論研究，關于分數階和分段光滑耦合作用下系統動力學特性的研究還很少。在含有分數階的分段光滑系統中，由于分數階和分段光滑系統非線性的雙重影響，其動力學行為的理論分析變得更加復雜，對于系統的周期解及其穩定性和系統參數對動力學性能的影響等很多問題還需要深入的研究。

本文以含間隙的分數階分段光滑碰撞振子為研究對象，將其簡化為一對稱的分段光滑模型，采用平均法獲得系統的周期解，并對其幅頻曲線的穩定性和跳躍現象進行研究，其次分析分段參數和分數階參數對系統振動性能及穩定性的影響，最后對分岔方程進行奇異性分析，得到系統的轉遷集和分岔圖。

1 系統動力學模型及近似解

圖1為含對稱間隙的分數階彈性碰撞振子，當振幅小于間隙δ時，只有主彈簧-阻尼系統起作用，系統作線性振動；當振幅大于間隙δ時，振子和副彈簧-阻尼系統反復接觸后又分離，系統呈現非線性振動，系統的動力學方程可寫為

式中:m為振子質量;k1f1(x)，c1f2(x)分別為分段光滑的彈簧力和阻尼力；KDp[x(t)]為分數階微分項;F為激振力，其中，

(2)

(3)

引入參數

原式(1)可變為

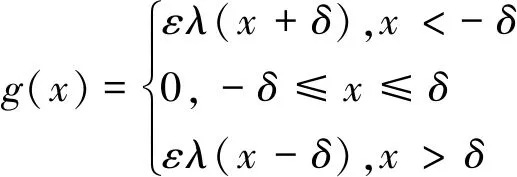
(5)

式(4)可變為

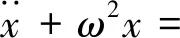
2μ1f2(x)-K1Dp[x(t)]]

(6)

設式(6)的解為

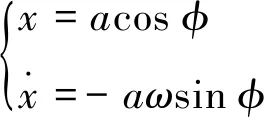
(7)

式中:φ=ωt+θ，則根據平均法可以得到

(8)

式中:δ=acosφ0。

(9)

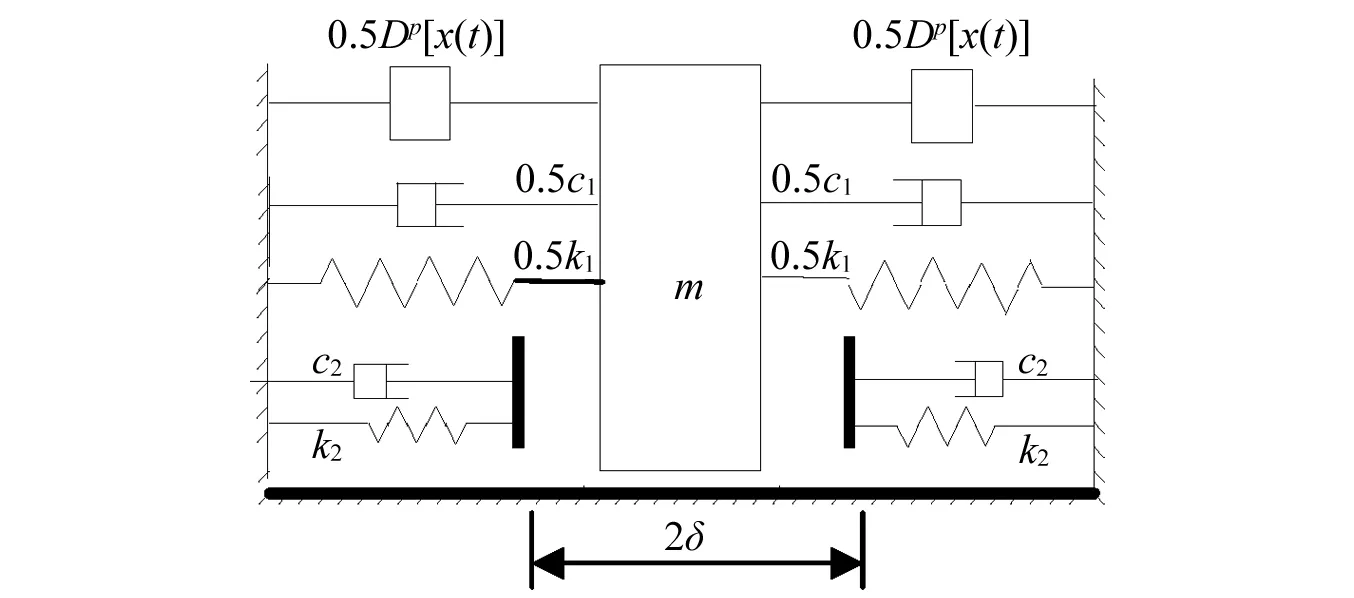
圖1 單自由度分數階分段光滑系統Fig.1 A single-degree-of-freedom piecewise smooth system with fractional-order derivative

式(8)第一部分P1的積分代表系統光滑的部分，第二部分P2的積分代表了系統非光滑的部分，第三部分P3的積分是分數階項的積分，這里采用分數階的Caputo定義對分數階微分項進行計算，形式為

(10)

這里Γ(z) 是Gamma函數滿足Γ(z+1)=zΓ(z)。可求得

(11)

其中，

(12)

式(12)代入原參數整理得到

(13)

(14a)

(14b)

C(a)，K(a)分別為系統的等效剛度和等效阻尼，由式(14)可知，等效剛度和阻尼均是由三部分組成。第一部分k1和c1分別為系統的主剛度和阻尼；第二部分k2H(a)和c2H(a)項分別為分段剛度和分段阻尼對系統的等效值，當a≤δ時，這部分為零，當a>δ時，這部分值的大小取決于分段剛度k2和分段阻尼c2，同時由于H(a)是振幅a的函數，且含參數δ，因此它的大小也受分段間隙δ和系統振幅a的影響；第三部分為分數階部分，顯然，分數階部分的大小取決于分數階系數K1和階次p。

2 數值仿真

選取系統參數m=10，c1=1，c2=2，F=3，k1=10，k2=15，δ=0.5，K1=0.1，p=0.5，根據式(13)畫出幅頻曲線，圖2中用實線表示。

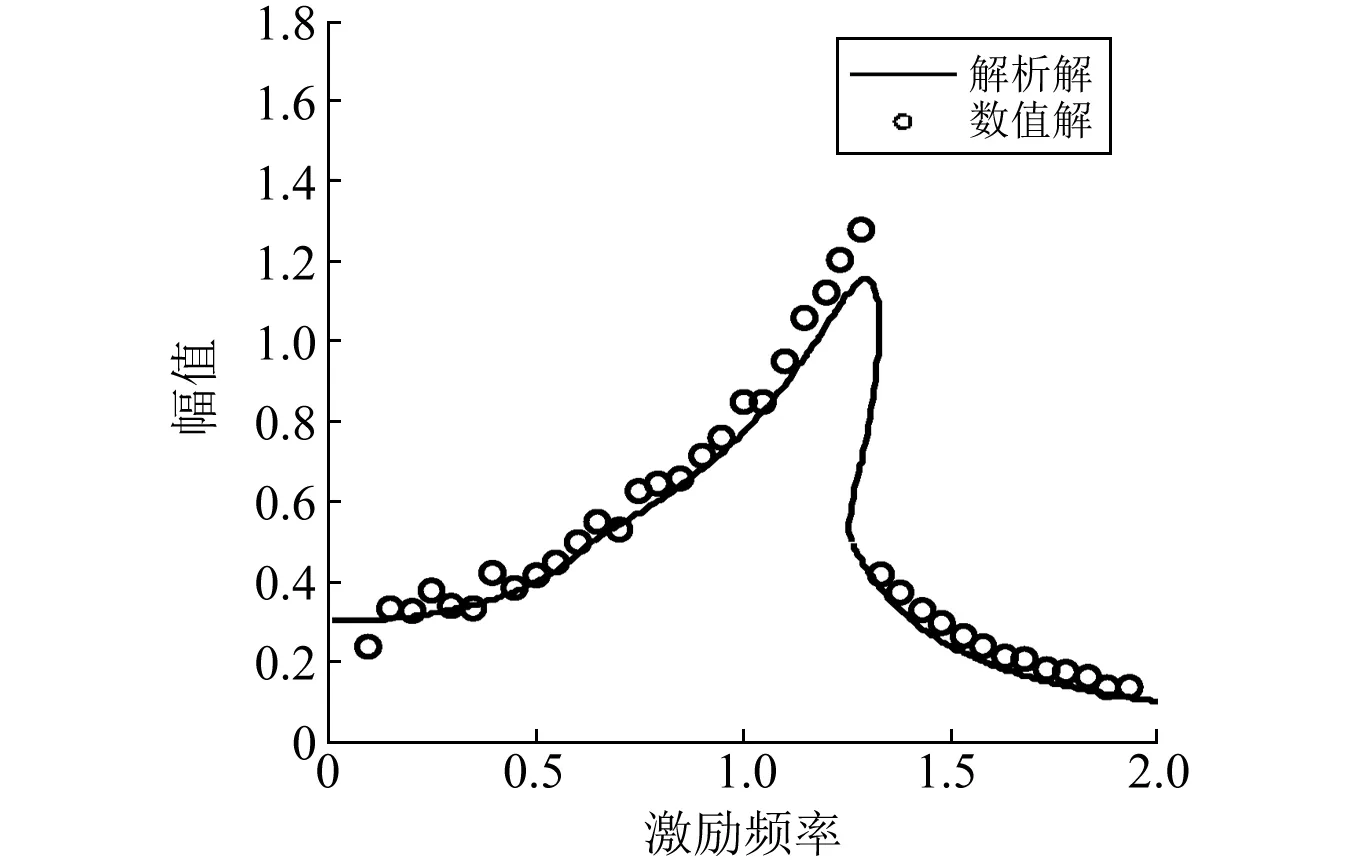
圖2 近似解和數值解對比圖Fig.2 Comparison of the solutions by analytical and numerical methods

為了驗證近似解的正確性，這里采用了文獻[22-23]里介紹的冪級數法進行數值研究，該數值方法的近似公式采用

(15)

(16)

3 穩態解及穩態解的穩定性分析

對于分段光滑的非線性系統，本文重點研究的是振子受迫振動的穩態周期響應，因此令

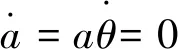
消除變量θ，求得系統穩態周期解的幅頻響應方程為

(17)

當a≤δ時系統為線性頻響特性，因此只考慮a>δ的情況。

(18)

(19)

由式(19)得到特征方程為

(20)

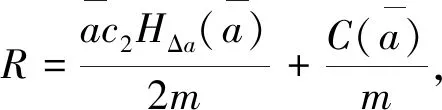
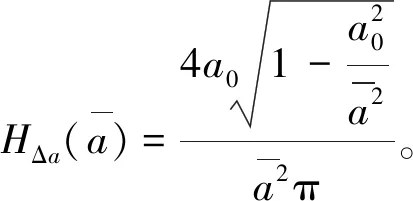
通過R，Q可以判斷周期解的穩定性，由于阻尼均為正，R?0，所以，特征值不可能出現一對純虛根，不會發生霍普夫分岔，我們只討論R>0的情況，為了方便觀察，畫出Q=0的曲線，用虛線表示。

(1)Q?于0，幅頻曲線和Q=0的曲線沒有交點。即幅頻曲線上的所有點均滿足Q>0，如圖3所示，此時沒有出現多解現象，周期解是穩定的。

(2) 隨著非線性的逐漸加強，幅頻曲線和Q=0曲線出現了交點，當只有一個交點時，處于跳躍的臨界狀態，當非線性繼續加強，出現兩個交點時，如圖4所示，幅頻曲線和曲線Q=0在A，B處相交，周期解的穩定性在交點處發生了變化，出現了鞍結分岔現象(交點A，B在幅頻曲線處有垂直切線)，A，B點即為穩定區和不穩定區的分界點。在Q=0曲線以外，幅頻曲線上的點均滿足Q>0，為穩定的周期解，而在Q=0曲線以內，幅頻曲線上的點使得Q<0，因此為不穩定的周期解。

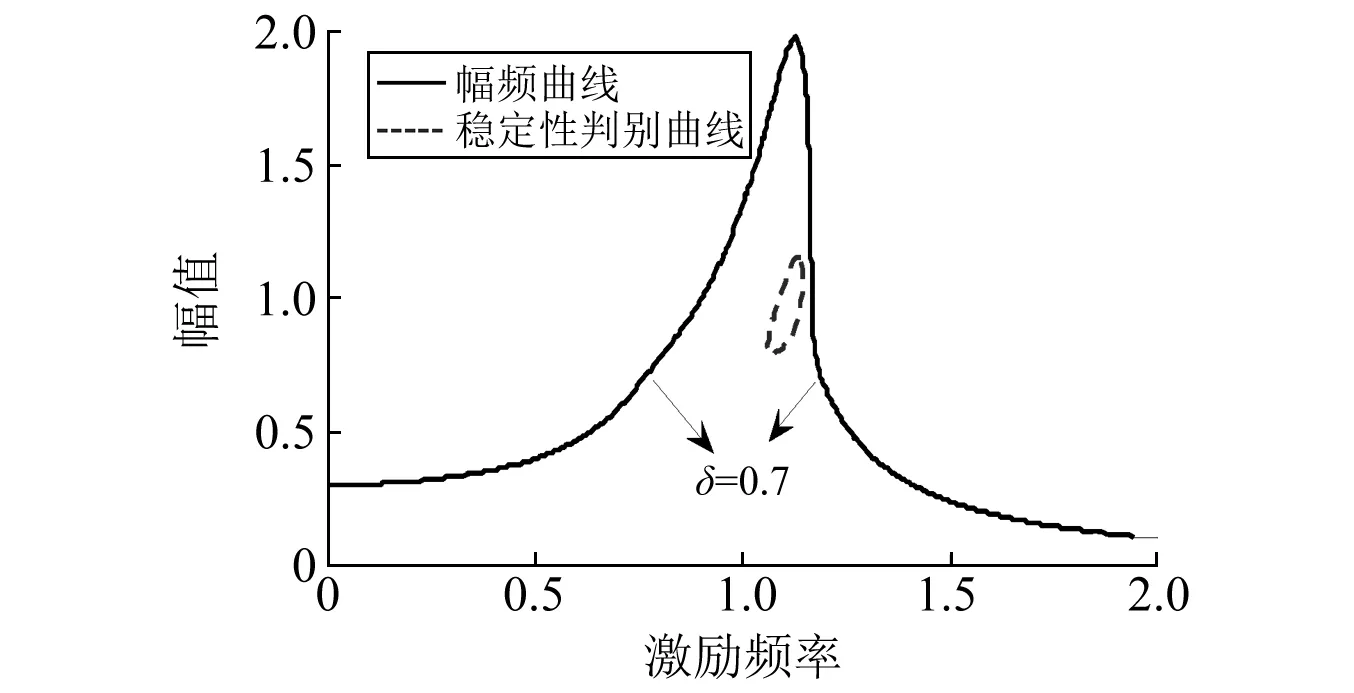
注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=5； δ=0.7；K1=0.1；p=0.5圖3 系統穩態解的幅頻曲線和不穩定區域(無交點)修改Fig.3 The amplitude-frequency curve and its stability region for the steady-state solution (no intersection)

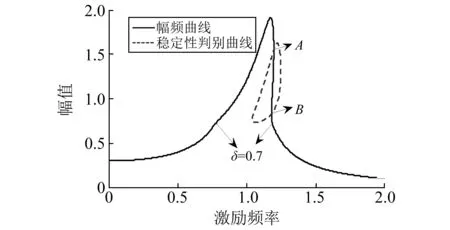
注：m=10;c1=1;c2=0.5;F=3;k1=10；k2=7； δ=0.7；K1=0.1；p=0.5圖4 系統穩態解的幅頻曲線和不穩定區域(有交點)Fig.3 The amplitude-frequency curve and its stability region for the steady-state solution (have intersections)

跳躍現象的產生正是由于存在著這種不穩定區域。出現跳躍時系統參數需滿足幅頻曲線相對于縱軸的斜率存在為零的點，即

(21)

對于分段光滑系統，在分段點δ處也可能出現分岔現象，當幅頻曲線對a的偏導在分段點δ處等于零時，B點和δ點重合，如圖5所示，即在δ處發生了鞍結分岔，系統參數需要滿足以下的關系

P=2{ω2C2(δ)+[mω2-K(δ)]2}+

δHΔa(δ){ω2c2+2k2[mω2-K(δ)]}=0

(22)

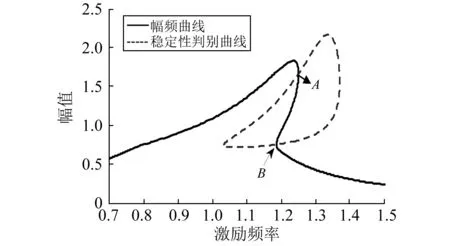
注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=30； δ=0.7；K1=0.1;p=0.5圖5 分段點發生鞍結分岔Fig.5 Saddle node bifurcation at the segmentation point

而當曲線Q=0和幅頻曲線相交于分段δ處，且P不等于零時，這時只有A點為鞍結分岔點，B點則為非光滑系統特有的擦邊分岔[24]，由于系統的幅頻曲線是由a<δ的線性部分和a≥δ部分的非線性曲線拼接而成的，因此在分段點處形成了尖角。如圖6所示。

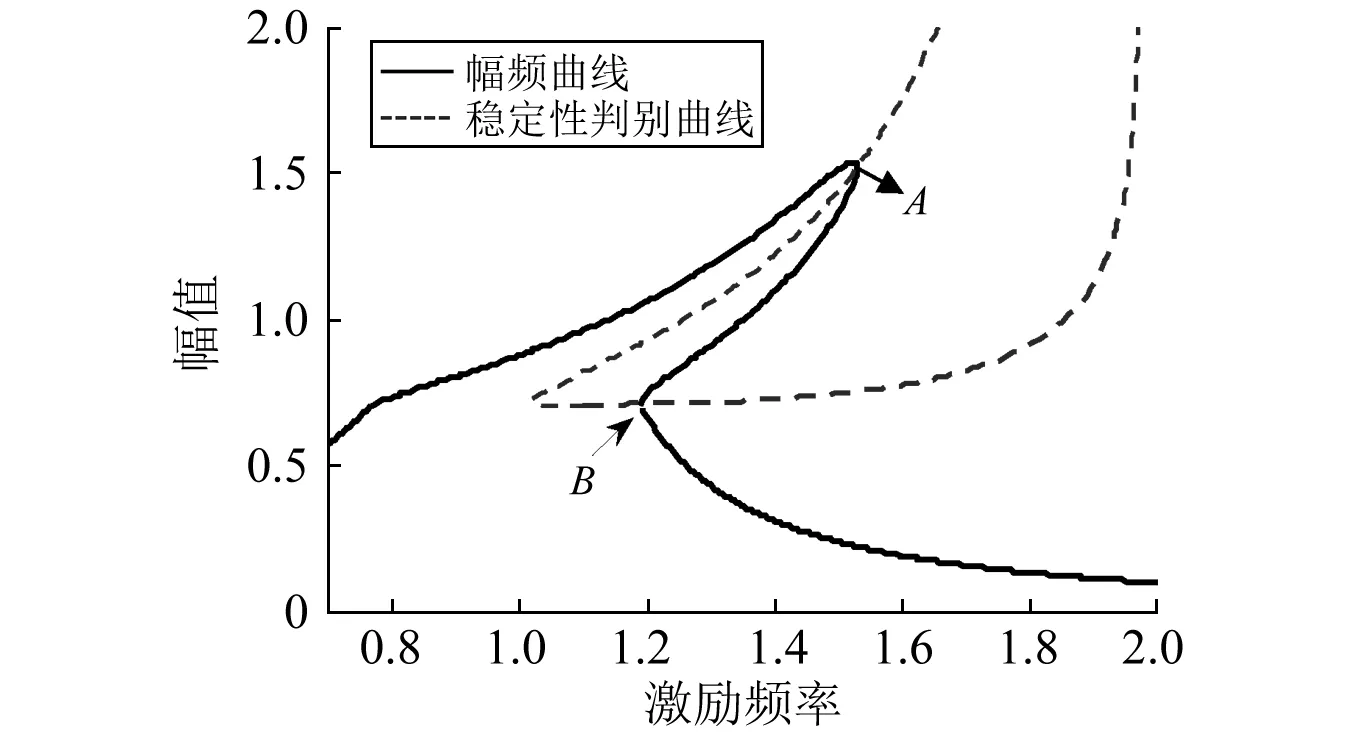
注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=30; δ=0.7;K1=0.1;p=0.5圖6 分段點發生擦邊分岔Fig.6 Grazing bifurcation at the segmentation point

4 參數分析

通過Q，R可以判別周期解的穩定性，系統的幅頻響應曲線在不穩定區域會發生跳躍，這種跳躍現象的產生正是由于存在不穩定區域，因此，設計系統時，應當避免這種不穩定區域的出現，或者減小不穩定區域。以下討論系統參數對不穩定區域和系統動力學特性的影響。由于系統參數較多，假設其它參數不變，首先分析分段剛度及分段阻尼對系統穩定性和動力學的影響。

圖7為分段剛度變化時系統的幅頻曲線和穩定性曲線Q。當k2=5時，曲線Q和幅頻曲線沒有交點，幅頻曲線沒有出現多解現象，此時幅頻曲線是漸進穩定的，k2=7時，判定條件Q曲線的范圍加大，即不穩定區域增大，被Q曲線圍起來的部分即為周期解的不穩定區間，其余處于Q曲線外部的部分是漸進穩定的，交點為穩定點，而非漸進穩定點，當k2進一步加大到9時，Q曲線的范圍也進一步增大，不穩定區域變得更大，同時，不穩定周期解的范圍也加大。另一方面，隨著非線性剛度k2的增大，共振區域也發生變化，系統共振頻率明顯加大，振幅峰值逐漸減小，振幅滯后現象愈發明顯，系統的非線性隨著彈簧剛度k2的增大而加強。

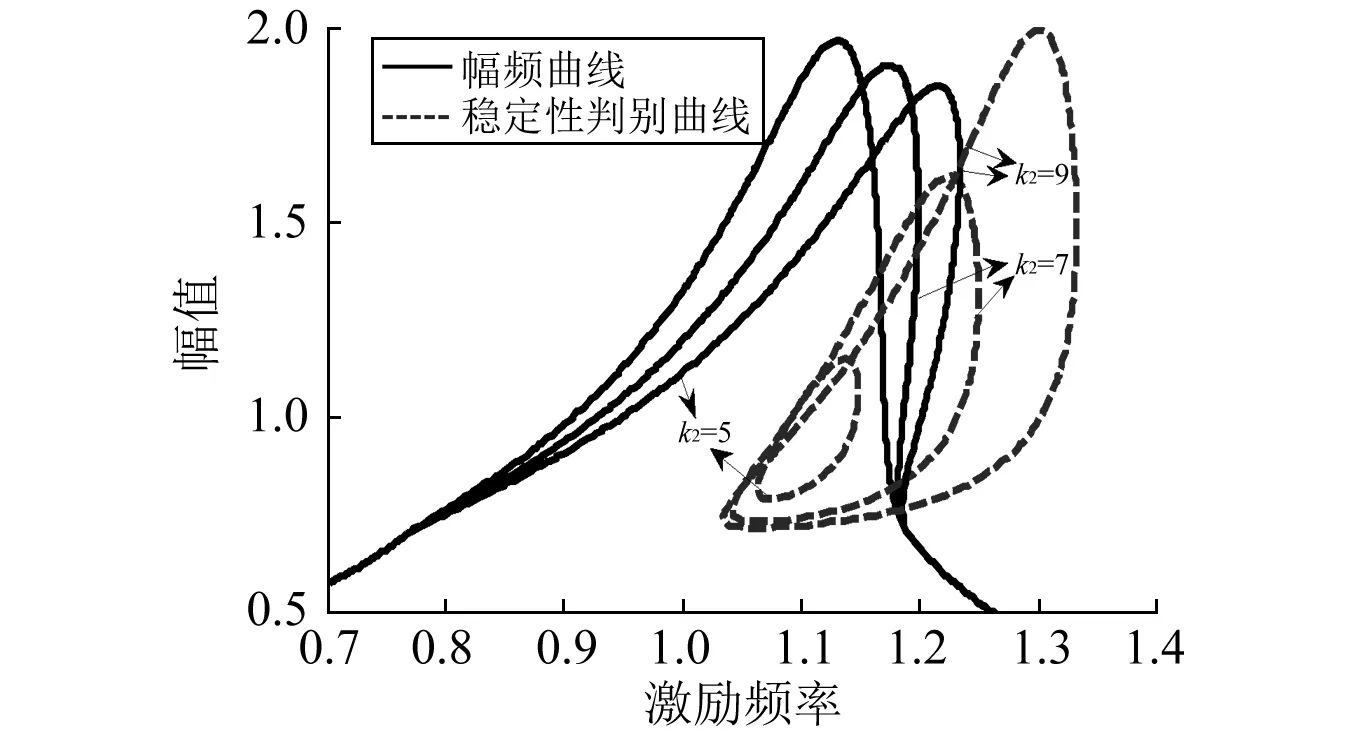
注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=5,7,9; δ=0.7;K1=0.1;p=0.5圖7 分段剛度對幅頻曲線及其不穩定區域的影響Fig.7 Effects of the piecewise stiffness k2 on the amplitude-frequency curves and their unstable regions

圖8為分段阻尼c2分別取1，3，5，7時，系統幅頻曲線的變化圖，從圖中我們可以看出，隨著分段阻尼c2的增大，系統的非線性特性并沒有大的變化，共振區的頻率范圍也幾乎沒有變化，但是系統的振動幅值明顯減小，共振頻率隨著分段阻尼c2的增大也逐漸減小，從圖3還可以看出，系統的不穩定區域隨著c2的增大也逐漸減小，達到一定值時，系統頻響曲線不再發生跳躍現象，不穩定區域消失。因此，可以通過加大分段阻尼c2來抑制系統不穩定區域的產生。

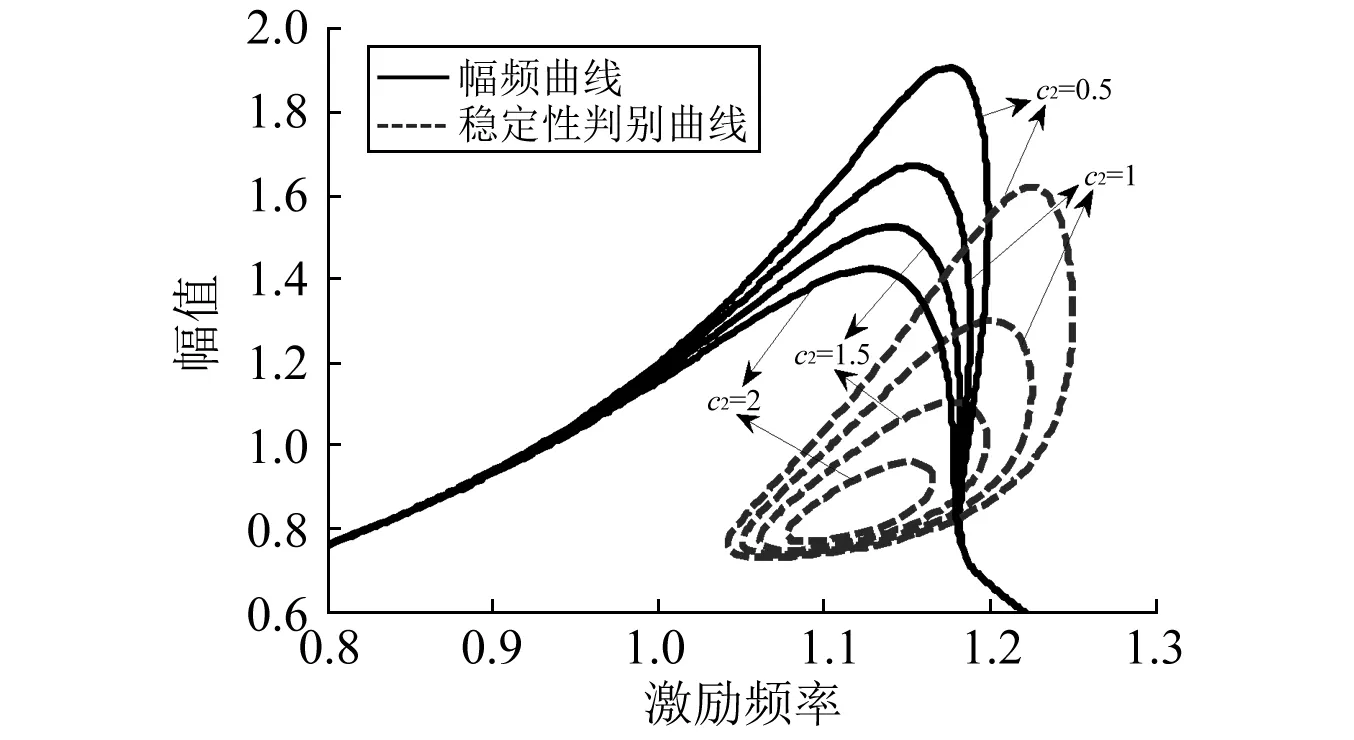
注：m=10;c1=1;c2=0.5,1,1.5,2;F=3;k1=10; k2=7;δ=0.7;K1=0.1;p=0.5圖8 分段阻尼對幅頻曲線及其不穩態區域的影響Fig.8 Effects of the piecewise damping c2 on the amplitude-frequency curves and their unstable regions

其次，分析分數階系數K1和階次p對系統振動和穩定區域的影響。保持其它參數不變，分數階系數K1分別取0.1，0.5，0.9時，系統幅頻曲線及穩定性判別曲線如圖9所示。顯然，當K1逐漸增大時，系統的非線性特性逐漸增強，且由式(14)可知，隨著K1的增大，系統的等效剛度逐漸增大，因此系統的共振幅值逐漸減小，同時，由于阻尼也隨著K1的增大而逐漸增大，導致系統共振頻率隨之逐漸增大，然而，共振區的頻率范圍卻隨著K1的增大而逐漸縮小。同樣由圖9可以看出，幅頻曲線的不穩定性區域隨著K1逐漸增大而逐漸減小。

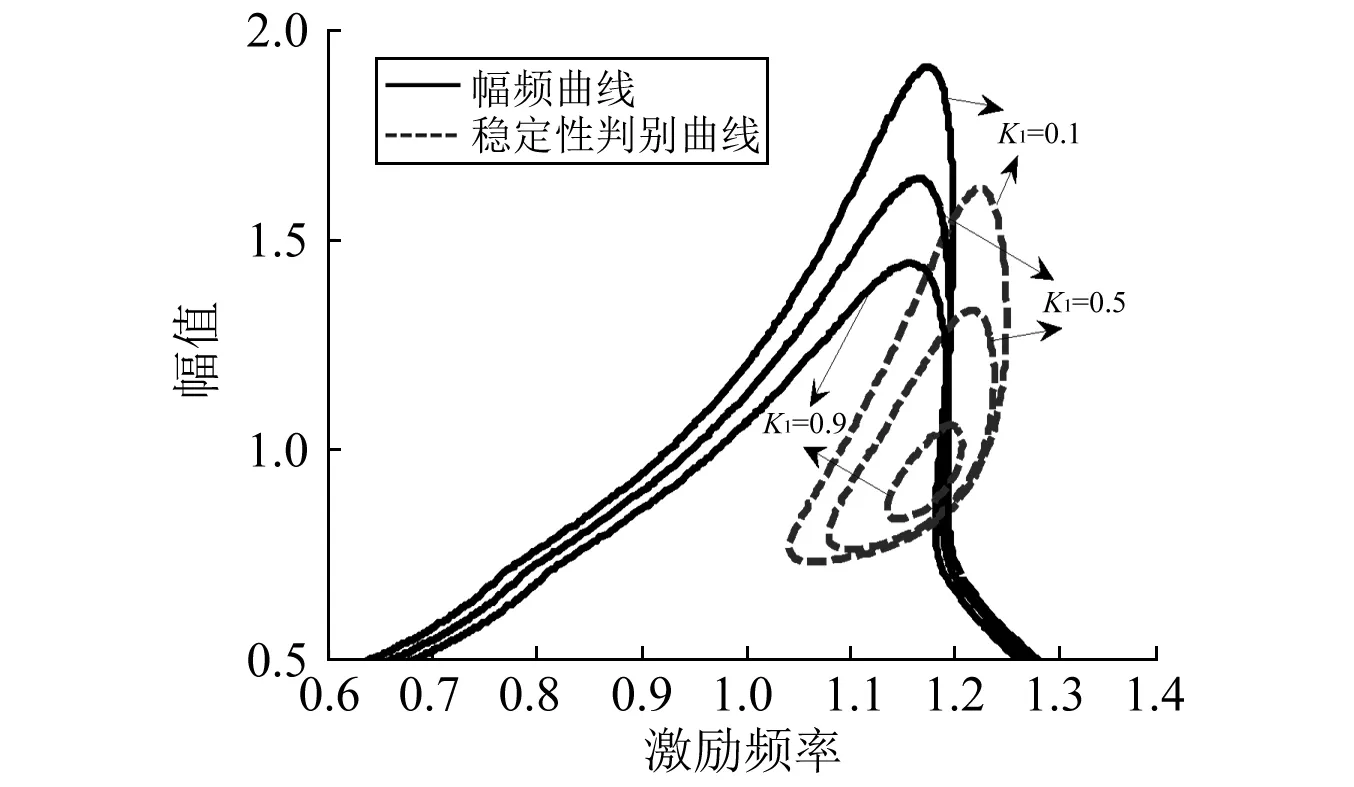
注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=7；δ=0.7； K1=0.1,0.5,0.9；p=0.5圖9 分數階系數對幅頻曲線及其不穩態區域的影響Fig.9 Effects of fractional-order coefficient K1 on the amplitude-frequency curves and their unstable regions

當分數階階次p分別選取0.1，0.5和0.9 時，周期解的振幅曲線和穩定區域判別曲線如圖10所示。隨著分數階階次p的增大，系統的非線性特性略有減弱，并由式(14)可知，系統的等效阻尼逐漸增大，因此導致系統共振振幅逐漸減小，同時等效剛度隨著p的增大而減小，引起系統共振頻率也逐漸減小。另一方面，隨著分數階階次p的增大，系統不穩定區域也在逐漸減小。因此，分數階系數K1和階次p對系統的共振振幅、共振頻率以及不穩定區域均有影響。

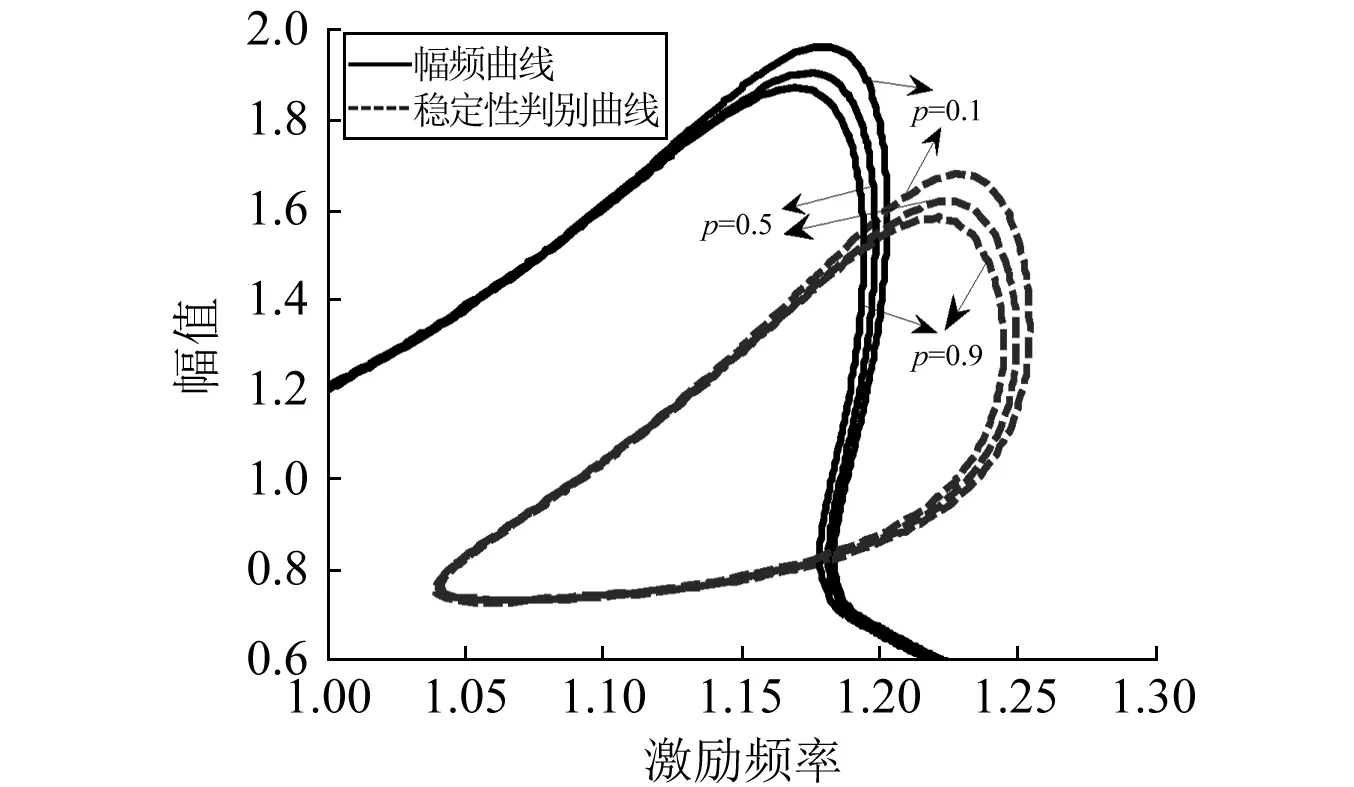
注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=7;δ=0.7; K1=0.1;p=0.1,0.5,0.9圖10 分數階階次幅頻曲線及其不穩態區域的影響Fig.10 Effects of the fractional-order order p on the amplitude-frequency curves and their unstable regions

最后分析分段間隙對系統振動特性的影響。保持其它參數不變，分段間隙分別取δ=0.3，0.6和0.9時系統的幅頻曲線及其相應的不穩定區域如圖11所示。隨著分段間隙的增大，系統的不穩定區域位置變化明顯，δ=0.3時對應的幅頻曲線和穩定判別曲線沒有交點，周期解是穩定的。隨著δ的加大，不穩定區域逐漸加大，周期解也出現不穩定性區域，并隨之擴大。另一方面，系統共振區域的頻帶變窄，共振頻率逐漸變小，共振振幅隨著分段間隙的增大明顯加大，但是當間隙過大，超過系統的共振峰值時，系統的非線性區域會消失，呈現出完全的線性特性。

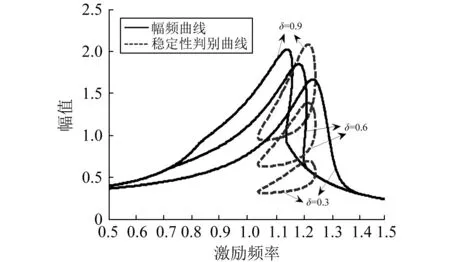
注：m=10;c1=1;c2=1;F=3;k1=10;k2=7; δ=0.3,0.6,0.9;K1=0.1;p=0.5圖11 分段間隙對幅頻曲線及其不穩態區域的影響Fig.11 Effects of the clearance δ on the amplitude-frequency curves and their unstable regions

5 奇異性分析

為了更全面地了解分數階分段系統主共振的頻響特性，以下應用奇異性理論分析主共振的分岔，找出系統參數變化對該分數階分段系統響應特性的影響規律。把幅頻響應方程在δ點進行泰勒展開，略去高次項后可以得到

b4a4+b3a3+b2a2+b1a+b0=0

(23)

其中，

b3=-2a0c2π(2+π)(c1+c2+(c1+c2-m)ω2+

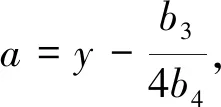
y4+d2y2+d1y+μ=0

(24)

其中,

y4+d2y2+d1y+μ=0是范式y4+μ=0的普適開折，有兩個開折參數d1和d2，根據奇異性理論，以下對此普適開折的持久性進行分析。

分岔點集：B=Φ;

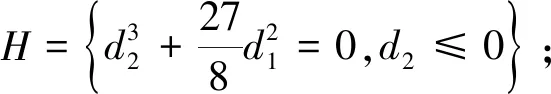
雙極限點集：D=Φ；

系統的轉遷集為：∑=B∪H∪D

系統的轉遷集及分岔圖如圖12所示。可以看出，轉遷集把二維開折參數d1,d2組成的左半平面(由于d2≤0)分成了兩個區域Ⅰ,Ⅱ，每個區域內系統的分岔是持久的，在分界線上，系統的分岔是不持久的。兩個區域內分別得到了如圖所示的Ⅰ1,Ⅰ2,Ⅰ3,Ⅱ1和Ⅱ2五種不同的分岔曲線，系統在不同區域的分岔曲線代表了系統在這些區域產生的不同的動力學行為，可以看出，在同一區域內得到的分岔圖都是拓撲等價的，不同區域得到的分岔圖是拓撲不等價的。系統呈現出的不同的分岔行為代表了系統在不同的參數作用下的動力學行為，通過改變系統的參數，可以改變系統的動力學行為，這可為合理選擇系統參數提供理論參考。

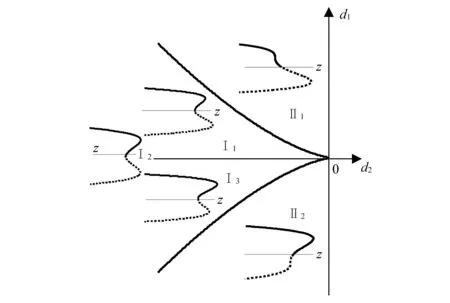
圖12 系統轉遷集及分岔圖(z=b3/4b4)Fig.12 The transion sets and bifurcation plots(z=b3/4b4)

6 結 論

本文建立了單自由度分數階分段光滑振子的力學模型，采用非線性求解方法得到了系統的周期解及其穩定性判別條件，并研究了周期解出現的跳躍現象及可能出現鞍結分岔和擦邊分岔；其次分析了系統參數對周期解及其穩定性的影響，結論如下：

(1)分段剛度和分段間隙對系統的非線性影響較大，分段阻尼對系統的非線性沒有影響，而分數階系數和階次對系統的非線性影響較小。

(2)分段剛度和分段間隙的增大會加大周期解的不穩定區域，而加大分段阻尼、分數階系數和階次則會抑制系統不穩定區域的產生。

(3)分段剛度和阻尼、分數階系數和階次的增大均會抑制系統共振振幅，而分段間隙的增大則會使共振振幅增大；分段剛度和分數階系數的增大會使系統共振頻率增大，而分段阻尼和間隙、分數階階次的增大則會減小系統共振頻率。

最后用奇異性理論對主共振的幅頻響應方程進行分析，得到了系統的轉遷集和該振動系統所有的分岔拓撲，系統在不同的參數作用下呈現出的不同的分岔行為，代表了系統在不同參數區間的動力學行為，改變系統參數，可以改變系統的動力學行為，這可為合理選擇系統參數提供理論參考。