航空發動機附件齒輪行波共振噪聲測量與分析

何劉海， 吳桂嬌， 王 平， 武昌耀

(中國航發湖南動力機械研究所 中國航空發動機集團航空發動機振動技術重點實驗室,湖南 株洲 412002)

中小航空發動機的附件從動錐齒輪故障率較高， 齒輪輻板裂紋故障占大部分，且都為高周疲勞產生裂紋，因此需要了解齒輪的共振頻率和共振轉速，避免出現重大故障事件。中小航空發動機轉速高，附件齒輪齒數較多，導致其嚙合頻率較高，甚至超過了20kHz，且中央錐齒輪副嚙合能量較大，容易激勵齒輪的高階模態。所以對附件齒輪行波共振進行測量與分析具有重要的理論和工程應用價值。

在目前的試驗中，齒輪行波共振頻率的獲取主要是通過測量加速度信號和動應力信號。加速度傳感器通常安裝在附件傳動機匣合適的位置測量齒輪副和軸系的振動信號[1-6]，通過信號處理技術如小波降噪、階次跟蹤等分析齒輪的振動特性，得到齒輪的行波共振頻率。這種測量方法雖然能反映部分的齒輪振動信息，但其主要有兩大缺點：其一，一般加速度傳感器的頻響范圍為1～10 kHz，齒輪的行波共振頻率遠遠超出了加速度傳感器的線性頻響范圍；其二，加速度傳感器安裝在附件機匣靠近齒輪的位置，考慮到傳遞路徑和噪聲信號的影響，其信號信噪比低，導致分析結果誤差較大。航空發動機附件齒輪輻板動應力測量方法也可以通過階次跟蹤分析出行波共振轉速[7]，但其成本高，試驗周期長，存在高速旋轉情況下，離心力會使應變片容易損壞，以及滑環引電器使用壽命有限等問題。

為了解決上述缺點，準確測量某航空發動機從動錐齒輪行波共振頻率和轉速，本文提出了一種新的測量方法，該方法通過聲波導管測量齒輪箱內部齒輪副振動產生的機械噪聲信號，采用時頻分析技術分析噪聲信號得到齒輪的行波共振轉速和頻率，并與通過有限元方法計算獲得的齒輪行波共振轉速作比較。最后，改變齒輪嚙合的邊界條件，分析齒輪各階行波頻率、幅值的變化，為優化設計、裝配提供參考。

1 行波共振理論

錐齒輪形狀和輪盤相似，很容易發生節徑型振動。根據薄板彎曲振動理論，在極坐標中，盤上某點的橫向位移為x，可用極坐標r，θ及時間t來描述[8-9]。設位移為

x(r,θ,t)=R(r) cosmθcospt

(1)

式中：R(r)為沿徑向變化的幅值；m為節徑數；p為自振角頻率。

由于振動時，節線上的位移為零，代入式(1)可得

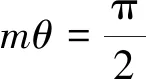
可見，節線與時間無關，節線在齒輪輻板上的位置是不變的，稱為駐波。由三角函數的關系，式(1)可以寫成

(2)

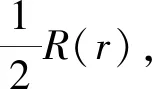
cos (mθ?pt)=0

(3)

由此可得余弦波節線相對于盤的角速度為

東亭的人們為這事感慨數日。迎賓大道說來也算是武漢最漂亮的馬路，修了幾輪，成了現在花團錦簇的樣子。車來車往，從不堵車。羅爹爹每天晨練要從迎賓大道過，經常夸說：“一走到這條路上，心里硬像是喝湯一樣舒服。”

(4)

可見，這兩個余弦波的節線(波形)以大小相等，方向相反的角速度在盤上旋轉，稱為動波。以上討論盤是不動的，即ω=0，當盤以角速度ω旋轉時，則行波相對于地面移動的角速度ω1，ω2為

(5)

(6)

此時的自振頻率p高于不轉情況的自振頻率。式中以角速度ω1旋轉的行波，其旋轉方向和盤旋轉方向一致，成為前行波；式中以角速度ω2旋轉的行波，其旋轉方向和盤旋轉方向相反，成為后行波。盤相對于地面振動的角頻率Ω1(或Ω2)應是ω1(或ω2)的m倍，即

Ω1=mω1=p+mω

(7)

Ω2=mω2=p-mω

(8)

或者

(9)

式中：ft為行波頻率(“+”對應于前行波，“-” 對應于后行波)；fs為固有頻率；n為轉速，r/min；m為節徑數。

采用靜止坐標系時，齒輪的節徑型振動是前、后行波節徑型振動，其固有頻率隨轉速變化。當前、后行波固有頻率和激振頻率相等，且激勵力方向和節徑振動方向一致時，就會發生行波共振。采用與齒輪同轉速同向旋轉的動坐標時，齒輪節徑型振動是駐波，齒輪的固有頻率簡稱動頻。

2 聲波導管原理

在聲學測量技術領域里常常要用到聲波導管,均勻截面聲波導管的主要優點之一在于[10-11]：當聲波頻率低于管的截止頻率時，能夠獲得良好的沒有衰減的平面聲波。管中平面波的獲得原理如下[12-13]：

設半徑為a的圓柱形管，一端無限延伸，管的徑向坐標為r，極角為θ，管軸用Z表示，則圓柱形管的聲波聲壓p的三維波動方程為

(10)

在剛性管壁的條件下，按照m階柱貝塞爾函數方程及其遞推關系，可求得管中聲壓解為

pmn=Amncos(mθ-φm)Jm(Kmnr)ej(ωt-kzz)

(11)

當m=0,n=0時

p00=A00ej(wt-kz)

(12)

p00即為沿Z軸直線傳播的(0,0)次平面波，其余稱為(m,n)次高次波。可以確定圓柱形管中聲波導管的截止頻率為

(13)

基于聲波導管的附件齒輪噪聲測量技術主要是基于管道聲學原理，將復雜環境下的機械噪聲通過專門設計的聲波導管傳遞出來，采用與管道壁齊平安裝或垂直安裝的普通傳聲器進行測量，獲得機械噪聲的平面波。

3 齒輪振動特性計算

本文的研究對象為從動錐齒輪，三維模型如圖1所示，其齒數為43齒。齒輪材料為12Cr2Ni4A，材料性能參數列于表1，工作時齒輪最高工作溫度為150 ℃，工作轉速為34 000～45 000 r/min。

表1 材料性能參數Tab.1 Material performance parameters

參考文獻[14-15]，采用十節點四面體單元對錐齒輪進行網格劃分，共有416 266個單元，619 297個節點，有限元網格見圖1。通過A，B兩個軸承安裝處的中間平面上一圈節點與各自中心軸線上的一個節點建立RBE2多點約束單元及中心節點創建接地彈簧模擬兩個軸承支撐面，彈簧的剛度系數即為軸承剛度系數，見表2。并且約束內花鍵處節點的周向位移。本次計算考慮的激振源為從動錐齒輪轉頻和齒輪副嚙合力。

圖1 從動錐齒輪模型及有限元網格Fig.1 Model and finite element mesh of the bevel gear

軸承名稱剛度/(N·m-1)軸向徑向雙內圈雙列角接觸球軸承5.20×1071.38×108

本文只給出從動錐齒輪在航空發動機最大轉速范圍內的節徑型振動，計算得到的模態(動頻)振型如圖2所示。當采用靜止坐標系時，齒輪的節徑型振動是前、后行波節徑型振動，其振型一樣，振型節線相對于齒輪輻板旋轉，從動錐齒輪行波共振振型、轉速及共振頻率的計算結果見表3。因計算的共振轉速為發動機燃發轉子轉速Ng，故以主動錐齒輪轉頻(發動機轉子轉頻)為基頻，則齒輪副嚙合頻率為38倍基頻(主動錐齒輪38齒)，即K=38，從動錐齒輪轉頻與基頻的倍數關系為K=38/43=0.884。

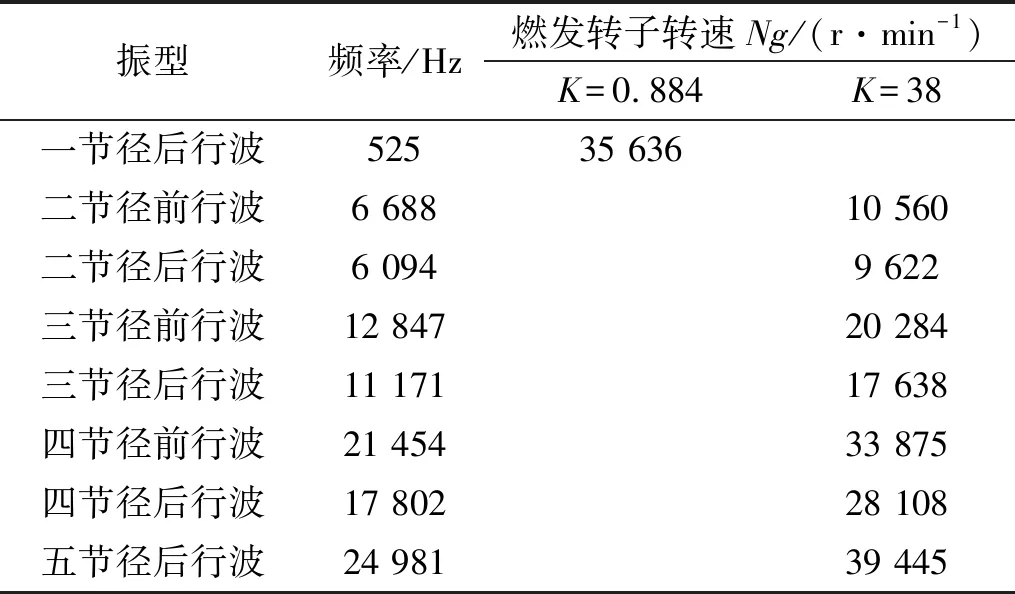
表3 齒輪共振轉速Tab.3 Gear resonance speed

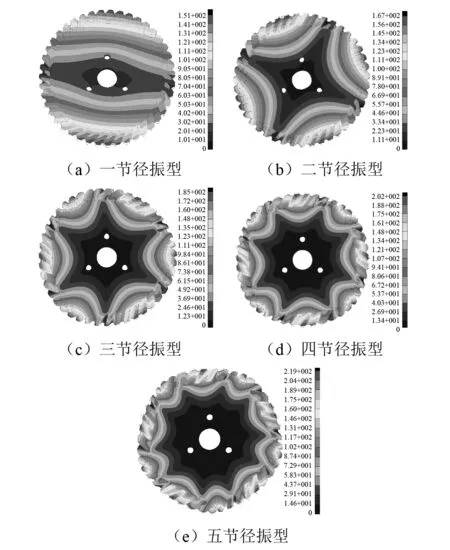
圖2 齒輪節徑振型Fig.2 Mode shapes of gear

4 測量方法及分析

4.1 測量方法

在齒輪嚙合過程中，齒輪的時變剛度、傳動誤差以及齒面摩擦等會引起齒輪的嚙合沖擊力，嚙合沖擊力激起齒輪振動并產生振動傳播，從而導致聲輻射。由于齒輪副嚙合是在附件傳動機匣內部，根據聲音傳播的特性，聲音在附件傳動機匣里將發生反射、折射、透射，因為附件傳動機匣內齒輪多，振動聲源豐富，且聲學邊界條件比較復雜，將會形成比較復雜的聲場，如果直接在附件傳動機匣外面測量聲信號，不僅信號失真，且背景噪聲比較大，獲取的信號信噪比低。

聲測法的試驗原理為：在附件傳動機匣靠近從動錐齒輪輻板處設計一個聲波導管，使得聲波導管一端靠近并垂直于從動錐齒輪輻板邊緣，另一端伸出機匣外。由于圓形管道的截止頻率與管道半徑成反比[16]，故設計導管半徑較小，使得管道的截止頻率較高，從而簡化了聲場，提高了信噪比。參考齒輪共振轉速的計算結果，本文采用的聲波導管半徑為8 mm，按式(13)算得平面波截止頻率為24.9 kHz，滿足試驗使用要求。把聲傳感器垂直于導管管道壁進行安裝，通過聲波導管直接測量齒輪機械聲信號。試驗結構原理圖如圖3所示。

聲信號測試分析系統包括聲傳感器、采集卡以及相配套的軟件分析系統。試驗器為某附件傳動試驗器，主要包括：起動電機、滑油箱、滑油泵、增速箱、聯軸器、某航空發動機附件傳動單元體(試驗件)、測試控制系統等。采用此測試設備，獲得的齒輪振動聲信息用聲壓和聲壓級來描述，聲壓是對一段時間內瞬時聲壓(存在聲波時，某一點上氣壓和平均氣壓的瞬時差)取均方根值，單位為Pa；聲壓級是使用對數標度來度量聲壓，可以表示聲振動能量的大小，單位為db。

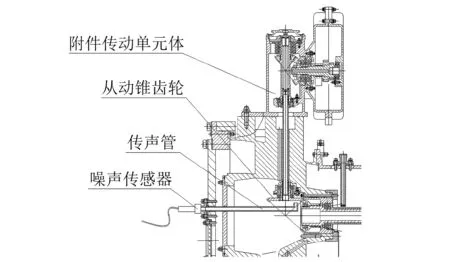
圖3 試驗原理圖Fig.3 Experiment schematic

試驗過程為轉速掃描試驗：試驗過程中緩慢推轉速，從起動一直推轉速到45 000 r/min(主動錐齒輪軸的轉速)，然后停車。試驗分兩次進行，兩次試驗只改變從動錐齒輪的裝配狀態，其余試驗條件不變。第一次從動錐齒輪的裝配狀態為：按照設計要求進行裝配，即錐齒輪組件在裝配時，緊固軸承座的4個自鎖螺母擰緊力矩為6 N·m，附件錐齒輪副齒隙為正常狀態；第二次從動錐齒輪的裝配狀態為：錐齒輪組件在裝配時，緊固軸承座的4個自鎖螺母擰緊力矩為1.5 N·m，且附件錐齒輪副齒隙為增大狀態，實際測得周向齒隙為0.42 mm。

4.2 試驗結果分析

第一次試驗的全過程時頻云圖如圖4所示。根據行波共振原理，節徑前行波頻率隨轉速升高而增大，節徑后行波頻率隨轉速升高而減小，故隨轉速變化，各節徑前、后行波頻率線關于各節徑動頻線對稱。結合計算結果，從圖中可以明顯看出三、四、五節徑的前后行波頻率線，由于背景噪聲(中低頻噪聲)的影響，一、二節徑前后行波不是很明顯。從圖4可知，各節徑行波在試車過程中一直存在，在沒有發生行波共振時，聲壓幅值很小，其原因是齒輪嚙合形成的沖擊是寬頻帶激勵源，它能夠激勵起各階行波，但其沖擊能量有限；再加上復雜環境激勵(隨機信號)，其分布到整個頻帶上能量也小，故行波響應幅值也小。

行波共振的判斷依據是：激勵(特征)頻率線和各行波頻率線的交點即為共振點，此時激勵頻率和前后行波頻率相等，振動能量變大，發動機的轉速即為共振轉速。從圖4可知，從動錐齒輪轉頻線(K=0.884)被低頻噪聲淹沒，故不分析。圖4中嚙合頻率線(K=38)和各階行波頻率線相交的點發生行波共振，此時嚙合頻率等于各行波頻率，聲壓幅值變大。圖4中標記的亮點即為二、三、四、五節徑前后行波共振區域。由試驗數據分析得到的試驗結果見表4。表4中的聲音幅值大小采用聲壓來描述，轉速均為主動錐齒輪轉軸的轉速，即激勵源(嚙合頻率)為38倍頻。從表4中可以看出，試驗結果和有限元計算的結果比較吻合，最大誤差為3.75%，彼此相互驗證了準確性。

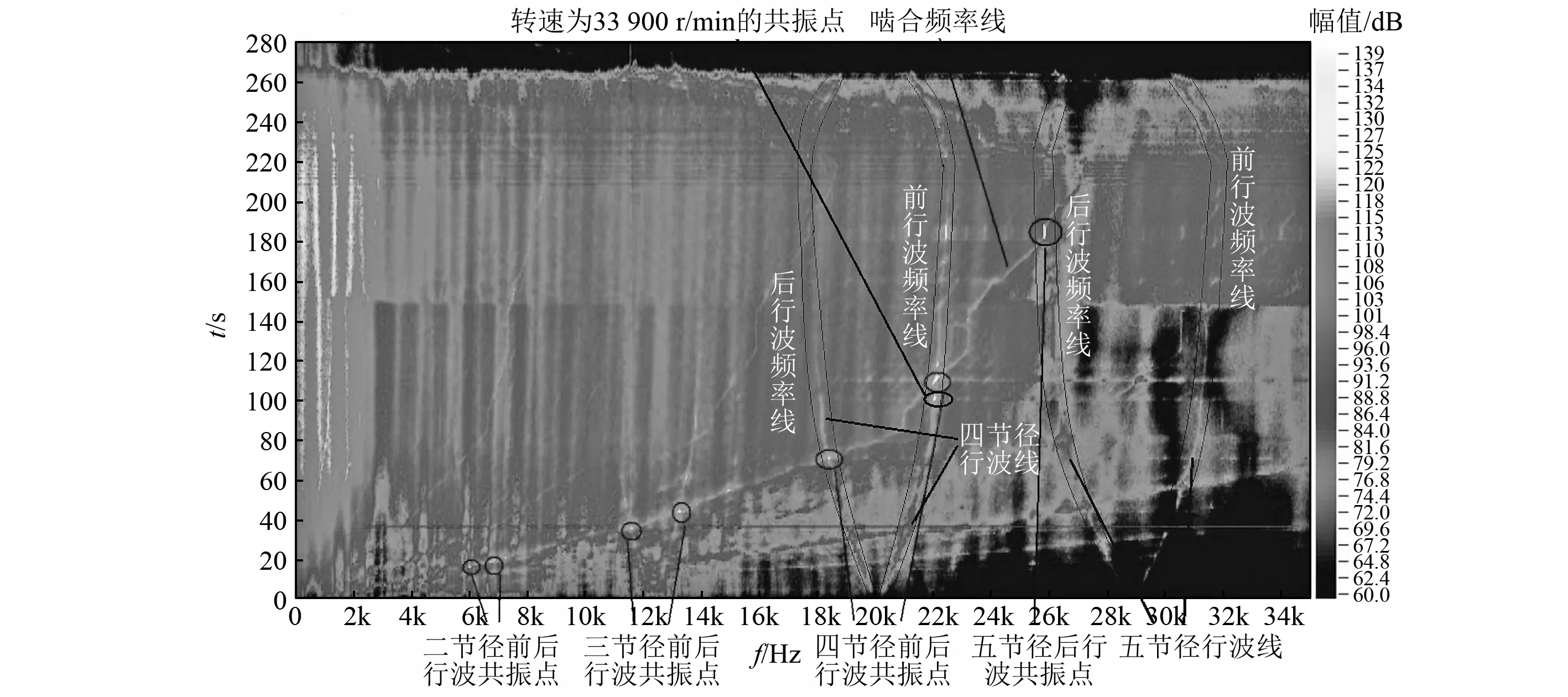
圖4 時頻云圖Fig.4 Time-frequency analysis

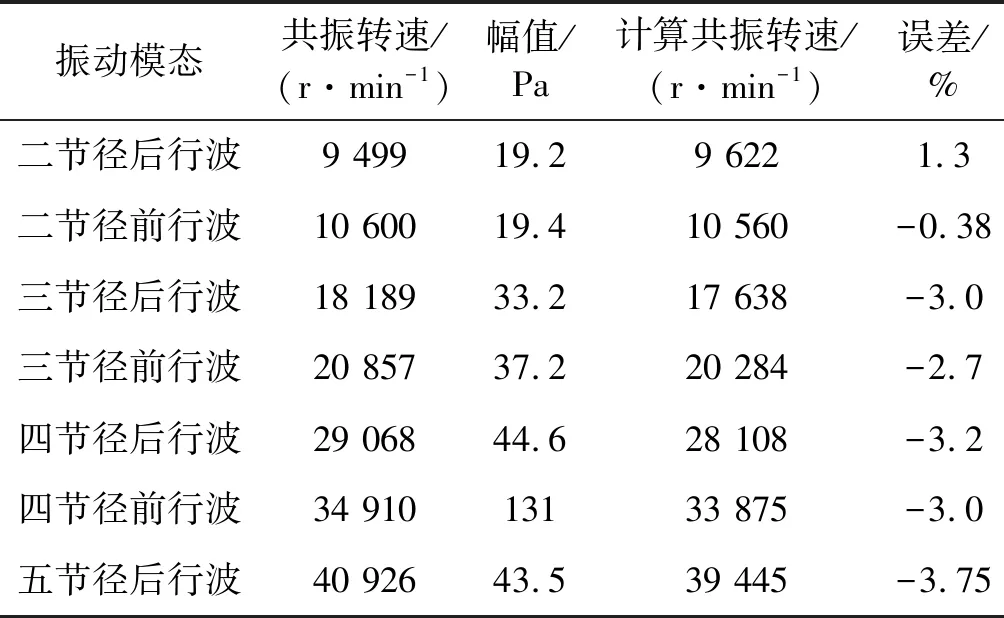
表4 聲測法測試數據(K=38)Tab.4 Test data based on acoustic signal (excitation source is the meshing frequency)

有限元計算只考慮了行波頻率線和激振頻率線K=0.884(轉頻)或K=38(嚙合頻率)相交的共振點，除此之外，從時頻云圖中可以看出，四節徑前行波頻率線在轉速為33 900 r/min時出現亮點，即能量變大，此時和行波頻率線相交的頻率線為嚙合頻率的邊頻線(K=39)，故可知共振激勵源除了嚙合頻率外，還包括嚙合頻率調制主動錐齒輪軸轉頻的邊頻帶，相應的頻譜圖如圖5所示。此時主動齒輪軸的轉頻為565 Hz，嚙合頻率為21 485 Hz，而行波共振頻率為22 050，相差軸轉頻，即邊頻。嚙合頻率和轉頻成38.026 5倍數關系，與理論值38倍有誤差，其原因是：①分析頻帶較高，譜線數有限，頻率分辨率較低；②試驗過程是快速推轉速，試驗轉速不穩，造成測試誤差。此時四節徑前行波共振聲壓幅值為87.3 Pa，相對于其他振型聲壓幅值較大，其原因可能是[17-18]：在這種邊界條件下， 四節徑前行波模態阻尼比小，同樣的激勵力產生較大的振動幅值，聲壓幅值也相應變大。根據時域信號波形以及頻譜邊帶形狀，可以看出振動信號產生了幅值調制。齒輪的幅值調制是由于齒面上的載荷波動、齒輪加工誤差(如齒距不均)、齒輪偏心以及齒輪故障所產生的局部性缺陷和均布性缺陷等因素引起的。故實際分析中需要考慮這些因素引起齒輪行波共振的可能性。

第一次試驗結果與第二次試驗結果對比情況見表5。由表中數據可知，改變從動錐齒輪的邊界條件，考慮激振頻率為K=38的情況下，齒輪的行波共振轉速變化不大，其中二節徑前行波共振轉速變化最大，為3.1%，高階行波共振轉速變化很小，均小于0.6%，最小為0.2%；而共振聲壓幅值從整體上看第二次要比第一次的結果大一些，其原因是在改變邊界條件下，齒隙變大，齒輪副的嚙合力增大，即激勵能量增大，共振能量相應增大。由于篇幅有限，故第二次試驗結果時頻云圖及頻譜圖不一一列出。

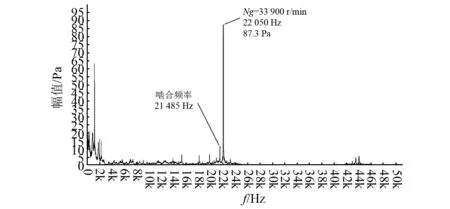
圖5 激勵源為嚙合頻率邊頻帶的行波共振頻譜Fig.5 Frequency spectrum of travelling wave resonance excited by mesh frequency band

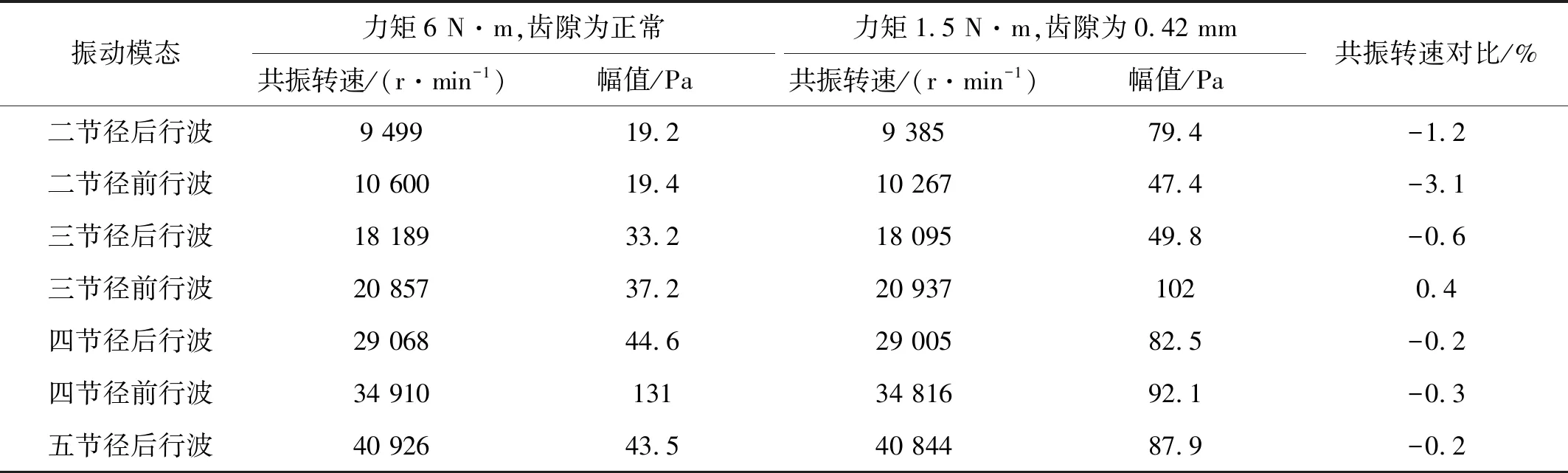
表5 不同邊界條件下的行波共振結果對比(K=38)Tab.5 Comparison of traveling wave resonance results under different boundary conditions(K=38)

5 結 論

針對從動錐齒輪行波共振轉速測量困難這一問題，本文提出了一種基于聲波導管的聲學測量方法，該方法采用聲波導管獲取封閉在機匣內的從動錐齒輪嚙合時產生的機械噪聲，通過機械噪聲信號的分析和處理，得到齒輪行波共振特性。通過理論分析和試驗研究，主要結論如下：

(1)對采集的聲信號做時頻分析，可以根據行波頻率線與轉頻線、嚙合頻率線的交點獲得各節徑前后行波的共振轉速，并且和有限元理論計算對比，共振轉速誤差均小于3.75%，可表明：測量方法有效，試驗結果準確。

(2)傳動過程中存在的齒輪嚙合沖擊力和復雜環境激勵(隨機信號)，可以激勵起各個節徑型振動，但能量很小，故時頻云圖中二、三、四、五節徑行波一直存在，沒有特征頻率線和它們相交時，能量有限，幅值很小。

(3)齒輪行波共振的激勵源除了嚙合頻率之外，還包括嚙合頻率調制主動軸轉頻的邊頻帶，它能夠激勵四節徑前行波產生共振，故齒輪存在磨損、偏心等故障時，會出現調制信號，激勵源變多，發生行波共振的可能性更大。

(4)在減小軸承座裝配力矩和增大齒輪副齒隙條件下，從動錐齒輪行波共振轉速變化(特別是高節徑行波共振轉速)很小，和原始邊界條件下相比，最大變化為3.1%，但共振聲壓幅值變大很多，故需要提高裝配要求，避免加大行波共振能量，造成齒輪高周疲勞破壞。