鐵路監測WSN網絡的非均勻優化分簇算法

呂安琪， 李翠然， 謝健驪， 段寶峰

(蘭州交通大學 電子與信息工程學院， 甘肅 蘭州 730070)

目前高速鐵路列車的時速已高達350 km/h，在確保高速列車安全運行方面，軌旁環境監測系統已至關重要。無線傳感器網絡WSN(Wireless Sensor Network)具有部署簡單、維護成本低、組網靈活、中繼轉發等特點，在軌道兩側部署基于WSN的環境監測系統可以高效、可靠地采集環境數據，從而對列車運行做出正確的防護措施。鐵路環境的特殊性使鐵路沿線部署的WSN網絡呈線型結構，同時由于WSN節點只能由電池供電，由此產生了“能量空洞”現象[1]，即網絡以多跳的方式進行信息傳輸，隨著跳數的增多，信息累積量增大，靠近Sink節點的普通WSN節點能耗大，其電能過早耗盡而導致網絡中斷的現象。如何構建合理的節點部署模型，有效降低甚至避免“能量空洞”現象，是鐵路沿線WSN部署研究亟待解決的關鍵問題。

關于線型WSN網絡中的“能量空洞”問題，已有大量研究成果。ZHANG等[2]提出一種基于信息融合的數據傳輸機制，通過控制信息粒度對原始數據進行不同程度的信息融合，從而減少傳輸數據量，節省傳感器網絡能量；劉安豐等[3]提出一種基于能量效率的高效節點部署算法，在已知網絡規模和節點感知距離的情況下，可求出最佳中繼節點部署和節點最優傳輸距離；文獻[4]通過節點休眠機制調整路由算法，從而提高網絡的能量利用率、可靠性以及實時性；在文獻[5]提出的能耗均衡算法中，采用了改進粒子群策略，對WSN中繼節點的位置進行尋優，均衡了節點能耗；文獻[6]以軌道交通為背景，提出基于布朗圓盤和Voronoi圖的幾何算法，通過建立兩棵傳感器樹形結構得到理想拓撲結構，延長網絡壽命，提高網絡性能。

上述文獻中，多假設節點隨機分布，并不適用于實際的監測環境。文獻[7]中以WSN節點的線性、均勻部署為前提，以節點轉發信息的能量消耗和能量平衡作為約束條件，采用非線性方法建立了一種線性WSN網絡調度策略以平衡節點能量消耗。王楠等[8]提出了一種等距分組多跳路由算法，建立了能耗數學模型，通過優化數據傳輸方式延長了網絡壽命。文獻[9]以鐵路環境為依托，通過非均勻分區方式調整各區內的節點數目，以達到均衡節點能耗和延長網絡壽命的目標。基于上述研究成果，本文著重從鐵路環境的監測應用角度出發，全面地考慮了直線軌道、弧線軌道監測區域內的節點非均勻優化分簇與部署，以簇頭負載均衡度和簇頭能耗平衡度為計算依據，確定了簇的大小和簇頭的優化位置。仿真測試表明，所提算法在均衡簇頭節點能耗和提高網絡通信效率方面性能較優，有效地解決了“能量空洞”問題，延長了監測網絡生命周期。

1 節點部署模型

針對鐵路環境監測，以直線軌道和弧線軌道監測為具體應用場景，需對WSN節點部署模型展開分析。本文給出的假設條件：設軌道長度為L(直線或弧線長度)，節點感知半徑為r，簇的數目為k，分別為c1,c2,…,ck。網絡中節點類型分為2類，即簇頭節點CH(Cluster Head)與簇成員節點CM(Cluster Member)，節點部署方式有:

(1) 直線軌道部署 首先是初始化CM節點位置。CM節點沿直線軌道單側部署，節點間距相等且小于2r，見圖1(a)，CM節點監測信息的采集。采用非均勻分簇算法(見下文)將監測區域劃分為不同的簇，并通過仿真篩選出合適的CH節點位置，見圖1(b)，CH節點位置坐標記為ci(i=1,…,k)，用于接收、處理和轉發簇內CM節點采集到的信息；di為第i個簇的覆蓋距離。CM節點將采集的數據發送至本地CH節點，本地CH將信息融合后傳輸至相鄰CH，通過多跳、轉發方式就可將信息傳輸至用于連接外網的匯聚節點Sink，即c1→…→ck→Sink。

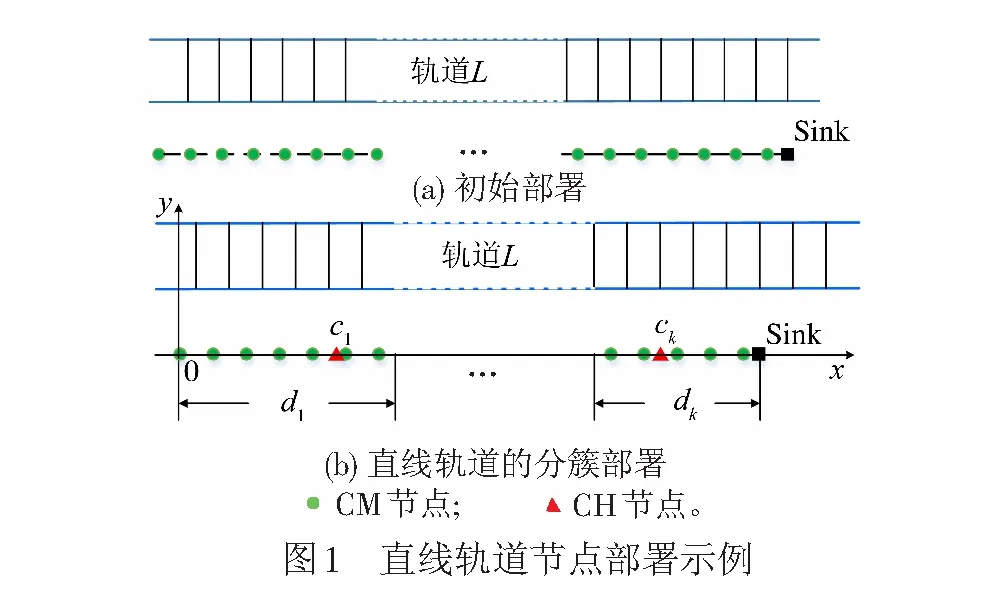
(2) 弧線軌道的分簇部署 CM節點沿弧線半徑R軌道單側等距部署，且相鄰CM間的直線距離小于2r，見圖2(a)。同樣通過仿真非均勻分簇算法(見下文)即可篩選出合適的CH節點位置，見圖2(b)中，O表示圓心，R為弧線軌道半徑，θi(i=1,…,k)為第i個簇的圓心角，弧線軌道WSN中的信息傳輸方式與直線軌道相同,(x,y)為傳感器節點坐標。

2 非均勻分簇算法

2.1 算法設計

假設WSN網絡中的CM節點具有如下性質[10]：

(1) CM節點同構，每個節點在單位時間內產生lbits數據，且均需發送至Sink節點；

(2) 節點具有相同的初始能量E0，僅考慮節點發送、接收數據的能量消耗，而感知與處理數據的能量消耗忽略不計，且不考慮數據傳送時數據的沖突和重傳；

(3) 節點間通信距離等于實際部署中兩節點間的直線距離。

節點采用典型的能量消耗模型[11]，發送、接收數據的能量消耗分別為

( 1 )

ER=lEelec

( 2 )

式中:ET為節點發送lbits數據消耗的能量;ER為節點接收lbits數據消耗的能量;α取值為 2時采用自由空間模型或α取值為4時采用多徑衰減信道模型;d0為區分兩種模型的距離閾值;d為收、發兩端的距離;Eelec為發射電路消耗的能量;εfs為自由空間信道模型功率放大系數；εamp為多徑衰減信道模型功率放大系數。

在需要監測的鐵路沿線(直線軌道或弧線軌道)等距部署CM節點，以均衡CH單位時間能耗為優化目標，對監測區域進行非均勻分簇，且所分簇間不發生重疊(即前一個簇的末端是下一個簇的始端)，并根據簇的覆蓋距離確定CH位置。非均勻分簇算法的執行步驟為

Step1沿待監測的軌道沿線等距部署CM節點。

Step2初始化簇1和簇2的相關參數(簇頭節點位置坐標c1、c2，簇的覆蓋距離d1、d2)。

Step3計算CH的位置坐標ck，k=3,4, …。

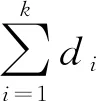
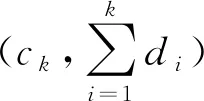
2.2 直線軌道的節點分簇

在直線軌道節點部署圖1(b)中，令ai為第i個CH節點與第i+1個CH節點間的傳輸距離，表示為

ai=ci+1-cii=1,2,…

( 3 )

當給定相鄰CM節點間的傳輸距離D時，則第i個簇內的CM節點數目Ni(取整后)計算為

Ni=di/D+0.5i=1,2,…

( 4 )

節點c1在一輪數據采集周期Tc內的能量消耗E1包括2部分，即接收d1區域數據的能耗Er1和傳輸數據至c2的能耗Et1,E1為

( 5 )

節點c2的單位周期能耗E2包括3部分，即接收d1區域數據的能耗、接收d2區域數據的能耗和傳輸數據至c3的能耗,E2為

( 6 )

當k=3,4, …時，節點ck的單位周期能耗為

( 7 )

當各CH節點的能耗滿足式( 8 )時，WSN網絡能耗達到均衡

E1=E2=…=Ek

( 8 )

根據式( 3 )～式( 8 )，可得到CH節點的位置坐標遞推式為

( 9 )

直線軌道情形下的節點非均勻分簇部署約束條件為

(10)

2.3 弧線軌道的節點分簇

在弧線軌道節點部署圖2(b)中，令hi為第i個簇對應的弧長，表示為

(11)

假設θci為第i個簇內的簇頭節點與初始點對應的圓心角，ai為弧線軌道上節點ci與節點ci+1間的直線傳輸距離，計算為

(12)

為相鄰CM節點間的弧線距離H為

H=2πR[2arcsin(D/2R)/360°]

(13)

則第i個簇內的CM節點數目Ni(取整后)計算為

Ni=?hi/H+0.5i=1,2,…

(14)

當各CH節點的能耗滿足式( 8 )時，WSN網絡能耗達到均衡。由此得到CH節點對應的圓心角遞推式為

(15)

假設弧線軌道的圓心坐標用(R, 0)表示，簇邊界坐標為(xi,yi)，CH節點坐標為(xci,yci)，其間的函數關系可表示為

(16)

弧線軌道情形下節點非均勻分簇部署約束條件為

(17)

繼而給出網絡生存周期和網絡效率的定義。

定義1網絡生存周期 網絡中第1個節點死亡的時間(節點壽命)。

定義2網絡效率 網絡壽命與網絡內CH節點數目的比值。

假設WSN網絡中的節點初始能量為E0，CH節點ci的單位時間能耗為Ei，則節點ci的壽命ti和網絡生存周期T分別為

ti=E0/Eii=1,2,…

(18)

T=min{ti}i=1,2,…

(19)

文中引入了簇頭負載均衡度B與簇頭能耗平衡度BH這2個參量，分別表示為

(20)

(21)

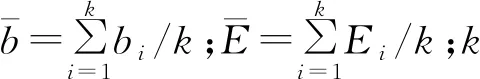
3 仿真分析

本節利用Matlab工具對提出的節點非均勻分簇部署算法進行仿真評估。具體仿真參數見表1[12]。

在直線軌道情形下，仿真得到了50組滿足式( 8 )CH節點能量均衡條件的數據，記為(ck， ∑di)。CH節點的能耗波動趨勢見圖3(a)。其中，x軸為數據組編號，1～50；y軸為對應組號的數據，即CH節點的位置；z軸為CH節點的單位時間能耗。能量等高線見圖3(b)，可見第37～50組的CH節點能耗波動最大且能耗最高，第1～14組的CH節點能耗波動次之且能耗較高；第31～36組的CH節點能耗波動較小且能耗中等；第15～30組的CH節點能耗波動最小且能耗最低。不同數據組的B/BH值見圖3(c)，進一步篩選出較優的數據組。

表1 仿真參數

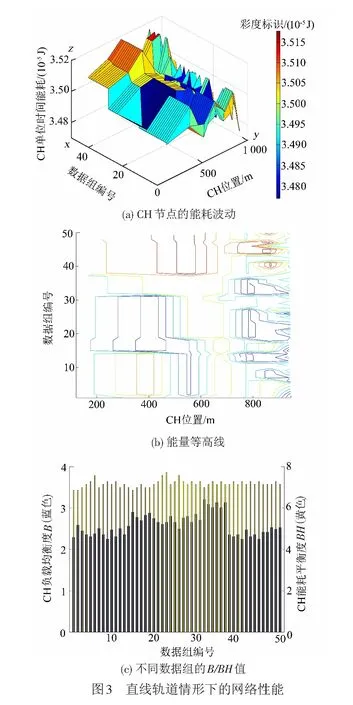
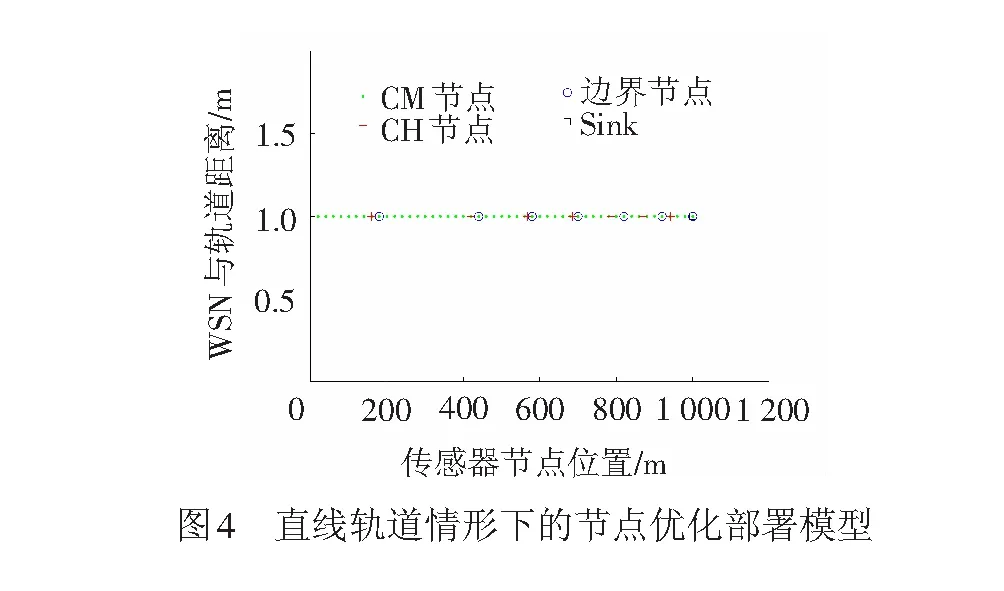
在篩選數據組時，先考慮CH節點能耗及其波動，再綜合考慮B/BH這2個參數值，由此得到較好的數據組號為16，17，20，24和28。可從以上5組數據中任取一組數據構建WSN網絡模型，以下仿真使用的是第28組數據，對應的(ck，∑di)取值為：(160，180)，(420，440)，(567，580)，(686，700)，(786，820)，(870，920)和(942，1000)，得到的節點優化部署模型見圖4。在綠色圓點與紅色加號重合的位置，可將該CM節點設定為CH節點，此時無需再另行放置CH節點。

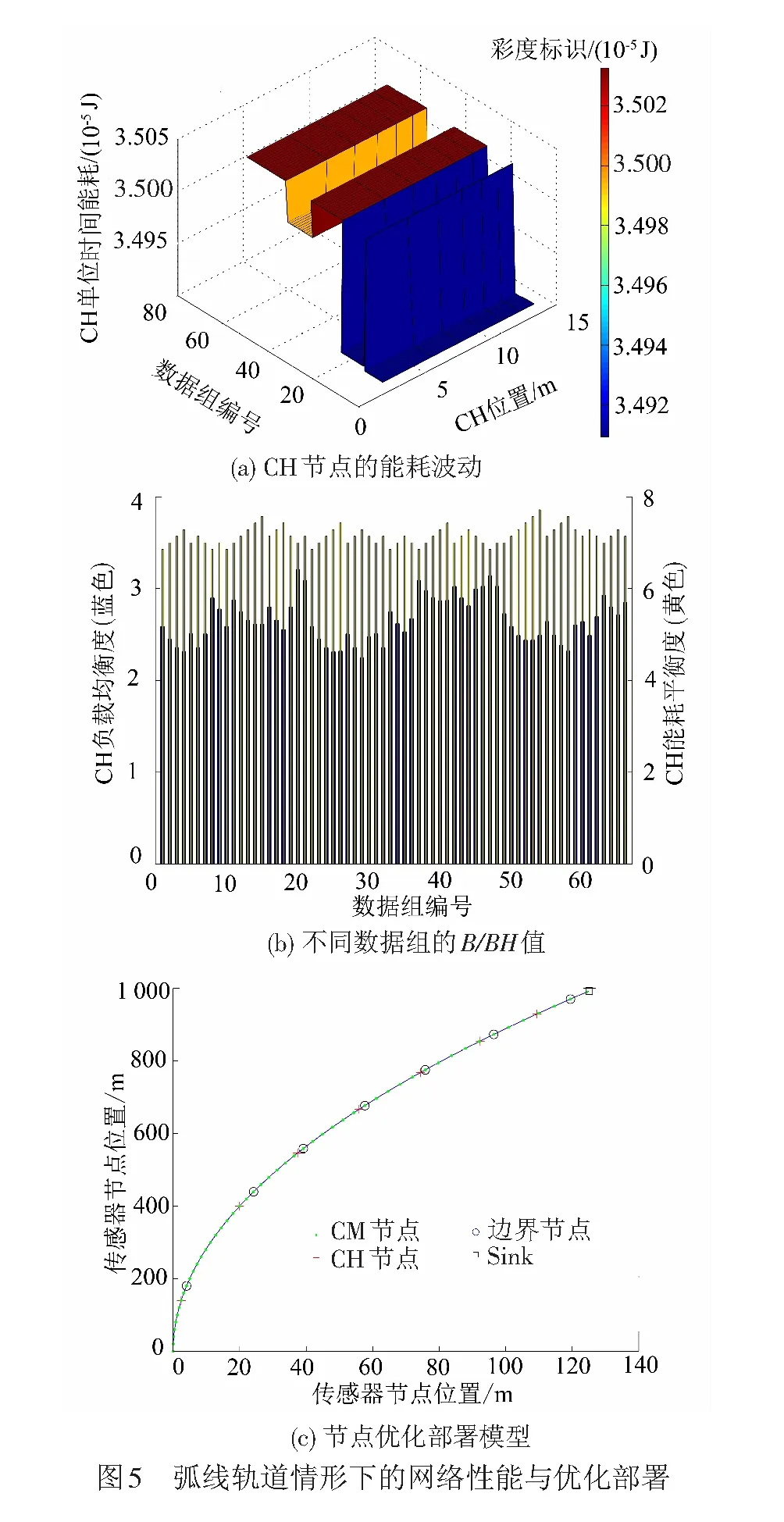
在弧線軌道情形下，通過仿真得到了66組滿足式( 8 )CH節點能量均衡條件的數據組，以CH的位置坐標(xci,yci)及其圓心角來標記。CH節點的能耗波動趨勢見圖5(a)。由圖5(a)可看出，沿弧線軌道部署的WSN網絡幾乎達到了理想的CH能量均衡狀態，其中，第1～9組和第10～21組的CH能耗最小。再結合圖5(b)給出的B/BH參數值，篩選出的較優數據組為第9組，對應CH坐標值為(2.4，140)，(20，399)，(37.4，545.7)，(55.9，666.5)，(74.3，767.5)，(92.3，854.5)和(109.4，929.2)，圓心角分別為2°、5.7°、7.8°、9.6°、11.1°、12.3°、13.4°，得到的節點優化模型見圖5(c)。圖中標識與直線軌道模型中的相同，不再贅述。

為進一步評估文中所提出的非均勻優化分簇算法部署效果，在相同簇數目情形下，不同算法構建的WSN網絡中的CH節點能耗、CH節點壽命和網絡效率分別見圖6～圖8。

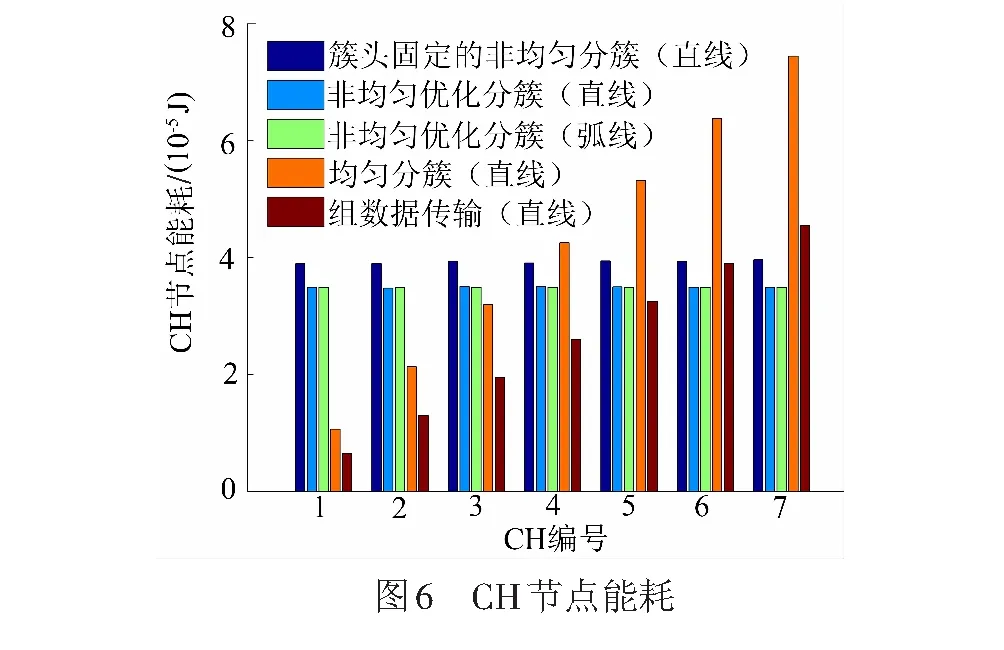
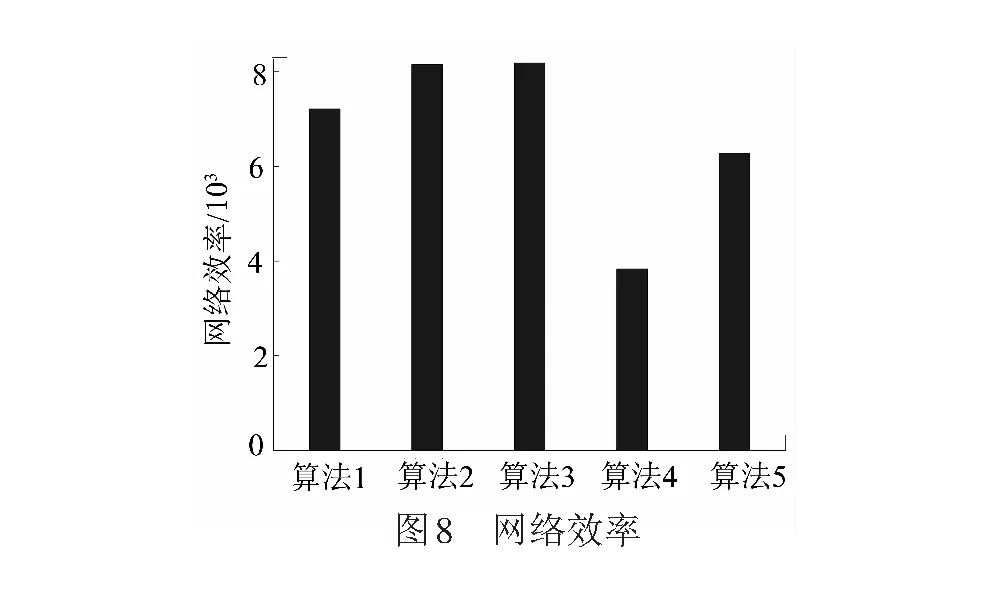
圖6中，簇頭固定的非均勻分簇是指CH節點位于簇幾何中心；均勻分簇是指WSN網絡中各個簇的覆蓋距離相等；組數據傳輸是指將網絡中的節點分組，數據由多條鏈路同時傳輸[13]。由圖6可見，均勻分簇算法和組數據傳輸算法的節點能耗呈非均勻態勢，組數據傳輸算法的節點能耗遠低于均勻分簇算法；文中算法與簇頭固定的非均勻分簇算法的節點能耗呈均勻態勢，所提算法在直線和弧線軌道部署中的節點能耗均低于簇頭固定的非均勻分簇算法。分析可知，組數據傳輸算法雖然降低了某些節點能耗，但無法消除節點能耗不均衡的現象，本文提出的非均勻優化分簇算法的節點能耗分布均勻且能耗低于組數據傳輸算法的最大節點能耗，具有較優的性能。

非均勻優化分簇算法在直線與弧線情況下的節點壽命相差無幾，仿真時會出現線條掩蓋現象，因此，圖7中選擇非均勻優化分簇算法(直線)與其他算法進行對比。由于網絡生存周期或節點壽命僅與最早死亡節點的時間有關，非均勻優化分簇算法的節點壽命最長，其次為簇頭固定的非均勻分簇和組數據傳輸算法，均勻分簇算法的網絡生存周期最短。

圖8中算法1～算法5分別對應簇頭固定的非均勻分簇、非均勻優化分簇(直線)、非均勻優化分簇(弧線)、均勻分簇和組數據傳輸算法。由圖8可明顯看出，非均勻優化分簇算法的網絡效率最高，簇頭固定的非均勻分簇和組數據傳輸算法次之，均勻分簇算法性能最差。

4 結束語

為解決鐵路沿線WSN線性部署導致的“能量空洞”問題，本文提出了一種節點非均勻優化分簇算法。算法以簇頭節點能耗、簇頭節點數目和簇成員節點數目之間的函數關系為基礎，構建了直線軌道、弧線軌道監測區域內的節點非均勻優化分簇模型，實驗結果表明，本文算法與簇頭固定的非均勻分簇、均勻分簇以及組數據傳輸算法相比，有效地降低了CH節點能耗、提高了網絡效率，延長了WSN監測網絡的生存周期。考慮到鐵路場景中相鄰站點間的距離較長，當簇數目增多時，算法性能會有所下降。下一步的研究將通過控制策略調整簇的覆蓋距離，并在鐵軌沿線每隔一定距離處增設匯聚節點Sink。此外，如何快速構建最優的非均勻分簇是面向鐵路應用的關鍵，進一步的研究思路是根據不同站點間的鐵路軌道長度和類型(直線、弧線)，評估算法的時間復雜度，以滿足鐵路應用的監測組網需求。