基于角色定位的講題教學與思考

孫 凱 殷容儀

(1.江蘇省蘇州市陽山實驗初級中學 215151； 2. 江蘇省蘇州市教育科學研究院 215004)

1 問題提出

近期，在江蘇省蘇州市第三期鄉村骨干教師培育站的培訓活動中，蘇州市教育科學研究院的數學教研員殷容儀老師給每位學員發放一張“學習材料”，內容為蘇科版初中數學教材上的9道簡單的例習題，要求學員們先做題，再思考怎樣講題，并邀請學員代表到講臺前模擬展示講題過程，其他學員觀察、思考、補充.上臺的學員結合自身教學經驗與思考，進行了常規性的講題展示. 其中有一道題，殷老師從角色定位的視角進行精彩的講題示范與點評，給學員們留下深刻印象.那么什么是角色定位，其主旨要義、適應特征與關注點有哪些，圍繞這些話題，筆者作了以下探索與思考，現整理成文，供各位同仁研討交流.

2 角色定位的內涵及適應特征

所謂“角色定位”，是指在分析和解決數學問題的過程中明確要求的目標元素是什么，把它定位成什么“角色”，以此確定探尋的路徑和求解的方法. 這里的“角色定位”特指在數學解題領域，比如求解一條邊長，需要考慮它的“角色”是直角邊？任意邊？高線？垂直平分線？角平分線？弦？特殊的邊？一般的邊？等.又如求解一個角度，需要考慮它的“角色”是內角？外角？對頂角？余角？等.這些分析思考問題的方式、方法都可歸納為“角色定位”.在解題過程中，能否對所求的元素進行合理的角色定位，決定了解題路徑的確定與問題解決的進程.因此，在講題教學中，引導學生抓住某個邊長、角度等關鍵條件，對求解對象進行角色定位嘗試，在明晰顯性角色的基礎上，積極挖掘隱形角色，實現合理、有效、精準地定位，啟發學生思維，突破問題思考的瓶頸.

這里所謂的“講題教學”指的是教師對題目進行講解，師生共同參與的一種旨在解決定向任務的教與學的方式.題目作為講題對象，其分類是多樣的.按課程內容可分為代數、幾何、統計概率和綜合實踐四類，按題型可分為選擇、填空和解答三類，按涉及知識可分為簡單類和綜合類，按問題情境可分為常規型和非常規型，按運用范圍可分為數學運用類和現實運用類等等.根據角色定位的內涵，我們認為其適應對象應具備“多角色”的特征，待解決的題目多出自于綜合類的幾何問題，求解的對象聚焦于線段、角等基本元素及相關元素.

3 教學案例

3.1 對“邊”的不同定位

圖1

原題呈現如圖1，在△ABC中，AC=BC=3，CE是外角平分線，點D是AC邊上的點，連接BD并延長與CE交于點E.

(1)求證：△ABD∽△CED.

(2)若AB=4，AD=2CD，求BE的長.

診斷分析在批改這道試題時發現異常情況，所帶兩個班級的90位同學中只有9位同學作出正確解答，這引起了筆者的關注.這道試題難在什么地方？學生的困惑是什么？如何幫助學生突破思考瓶頸？

此題改編自2010年四川省南充市中考數學第19題，原試題為：如圖2，△ABC是等邊三角形，CE是外角平分線，點D在AC上，連接BD并延長與CE交于點E.(1)求證：△ABD∽△CED.(2)若AB=6，AD=2CD，求BE的長. 顯然此題是對原試題的等邊三角形作一般化的處理，增加了求解BE的難度.此題考查了等腰三角形、直角三角形、相似三角形等基礎知識，內涵豐富，把BE作不同的角色定位，會發現多種不同的解法.在講題時，緊緊圍繞“角色定位”的講題策略展開教與學，主動為學生搭建交流展示的平臺，展示過程中，努力使學生的思維可視化、系統化、邏輯化，促使他們積極參與高階思維活動.

圖2

圖3

圖4

師：根據題目中的條件與(1)的結論，我們可以獲得以上新的條件，如何讓這些條件與BE建立聯系，把BE定位為什么樣的角色分析求解呢？

生1：在現有圖形中，直接求解BE是有難度的，我打算以BE為邊，構造直角三角形求解.作EG⊥BF、AH⊥BF、CQ⊥AB，垂足分別為G、H、Q，如圖3.構造△EGC∽△AHB，分別求得CQ、EG，Rt△ECG中求得CG，最后在Rt△BEG中，確定BE.

點評構造以BE為邊的Rt△，作EG⊥BF是最容易想到的輔助線，但是要在Rt△BEG中需先解決EG、BG的長，構造三角形相似模型幫助解決是個很好的辦法，但在實際分析求解時，用“等積法”求得AH的長是很關鍵的一步.

生2：我也是以BE為邊構造直角三角形來求解的.作EG⊥BF、CQ⊥AB，垂足分別為G、Q，如圖4. 借助△ECG∽△CBQ，先求CQ，再求EG，最后在Rt△BEG中，確定BE.

點評把BE定位為Rt△BEG的斜邊，與生1的解題策略類似，構造三角形相似模型解決EG、BG的長.顯然，這種構造相似的方式比解法1更簡捷，求解相對更簡便.實際分析問題過程中，能否發現∠ECQ=90°的基本“模型”，是構造三角形相似的關鍵，也是解題的關鍵.這個“模型”與“一線三等角”模型有相似之處，教學中可以作比較鑒賞.

圖5

圖6

圖7

生3：以BE為斜邊，構造Rt△ABE求解.作CQ⊥AB，垂足為Q，連接AE，如圖5. 易證四邊形AQCE是平行四邊形，以此證得四邊形AQCE是矩形，在Rt△BAE中根據勾股定理求得BE.

點評△ABC作為等腰三角形，高線CQ是最常規的輔助線，在分析問題過程中，發現AQ與EC位置與數量上都有特殊的關系，連接AE建構出特殊的四邊形(矩形)，以此構造以BE為斜邊的直角三角形，以斜邊的“角色”直接求之.

點評在分析問題過程中，發現BQ與EC在位置與數量上都有特殊的關系，聯想到建構三角形全等模型解決問題，把BE看成“倍分”線段求之，很巧妙.

生5：我以BD為邊，借助BD建構相似三角形求解BE.作CQ⊥AB、BK⊥AC，垂足分別為Q、K，如圖7. 根據“等積法”求BK，在Rt△ABK中，根據勾股定理求得AK，最后在Rt△BDK中求得BD，再求BE.

點評在(1)中我們發現BD=2DE，如果能求得BD或DE的長，就能求得BE的長，如何求BD的長呢？以BD為邊，建構直角三角形，利用等積法、勾股定理、相似三角形等，分別求得另外兩條邊長，BD求得后再求BE，水到渠成.

3.2 對“角”的不同定位

原題呈現如圖8，AB是⊙O的直徑，弦CD交AB于點E，∠ACD=60°，∠ADC=50°.求∠CEB的度數.

圖8

圖9

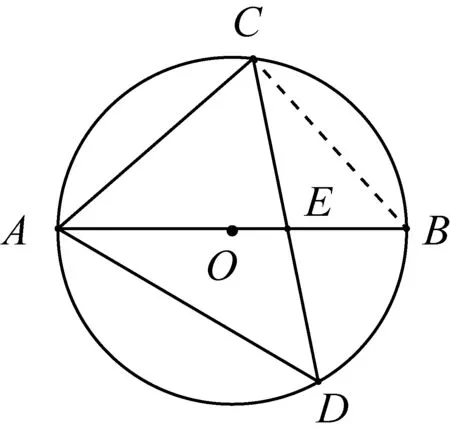
圖10

診斷分析這道例題出自蘇科版數學九年級上冊P57的例2，設計意圖是呈現問題情境，驅動學生自主運用圓周角性質定理解決求角問題，以聯系、梳理、整合知識，優化認知結構.由AB是直徑，學生會習慣性添加輔助線BD或BC，見直徑想直角，這是很好的數學思考習慣，是對數學知識熟練掌握的自然真實反應，值得肯定.但是，盲目的添加輔助線，在某些思考階段會干擾學生的數學思考，比如追問為什么連接BC，多數學生會回答構造90°的圓周角，至于還有什么目的就說不清楚了.圓中的∠CEB既不是圓心角，也不是圓周角，如何求解？對學生而言，是有一定難度的.

講題過程呈現題目，獨立思考五分鐘.

師：已知的條件有哪些？求解的對象是什么？

生1：AB是直徑，∠ACD與∠ADC的度數，求∠CEB的度數.

師： 由已知條件，你想到什么？

生2：由∠ACD和∠ADC，可求得∠CAD，但是要求的∠CEB與∠CAD沒有直接的數量關系，說明條件不夠，是不是要考慮使用AB為直徑的條件.

生3：由AB是直徑，可以連接BD或BC，這樣會得到90°的圓周角.

師：請把已知的條件在圖形上作標記，思考如何求解？有哪些方法？

生4：連接BD.

師：為什么連接BD，你是怎樣想的？

生4：……(不知如何作答)

師：求解對象是∠CEB，從位置上看，它是一個什么樣的角？請你說說看.

生5：它是一個外角，若連接BC，也可以看出一個內角.

生6：與∠AED互為對頂角.

師：大家說的非常好，根據∠CEB的位置特征，把它定位成不同的“角色”，就決定了求解它的策略與路徑，結合你添加的輔助線，說說你的想法.

生7：如圖9，連接BD，則∠ADB=90°.連接BD的目的是把∠CEB定位為△BDE的外角，則有∠CEB=∠ABD+∠CDB，需分別求∠ABD和∠CDB，此時∠ABD與∠ACD、∠CDB與∠ADC有直接的數量關系，問題得以求解.

生8：∠CEB也可以定位為△CAE的外角，則∠CEB=∠ACD+∠BAC，其中∠BAC可以轉換為∠BDC，利用互余關系，求得∠BDC即可.

生9：如果把∠CEB看成∠AED的對頂角，再把∠AED看成△ACE或△BDE的外角也可以求解.

師；有的同學連接BC，說說你是怎樣想的？

生10：如圖10，連接BC，則∠ACB=90°.連接BC的目的是把∠CEB定位為△CEB的內角，需求∠ABC與∠BCE，此時∠ABC與∠ACE、∠ABC與∠ADC有直接的數量關系，根據三角形內角和定理可求解.

師：輔助線的添加能夠賦予∠CEB豐富的角色，對∠CEB進行不同的角色定位，決定了不同的求解策略和路徑，希望同學們能夠好好運用角色定位的方法，幫助分析和解決問題.

點評在講題過程中，給學生充足的思考時間，以“角色定位”的視角引導學生把握問題的本質，在高階思維活動中探尋解題策略，提升學生分析和解決問題的能力.

4 教學思考

4.1 角色定位的主旨要義

在講題教學中，應搞清楚講題的目的.講題作為一種教學行為，其目的是引導學生經歷問題的分析和解決的過程，啟發思考，點撥、提煉和歸納方法，以幫助學生形成獨立解決問題的能力.從某種意義上看，講題教學的目的是教會學生解題.角色定位作為一種重要的分析和解決問題的方法，意在幫助學生探尋有效解決問題的方案，形成策略.波利亞的“怎樣解題表”把解題分為四個步驟：理解題目、擬定方案、執行方案、回顧.在這四個步驟中，擬定方案尤為關鍵.角色定位相當于“怎樣解題表”中的擬定方案，具體表現為深入理解題目并探求解題思路.

基于角色定位的講題教學，其目的可以劃分為兩個層面：一是知識與技能層面，教會學生運用所學基礎知識與基本技能解決數學問題；二是思維與方法層面，引導學生在問題解決過程中學會數學地思考，掌握思想方法，培養數學思維能力.顯然，前者屬于低階思維活動，而后者屬于高階思維活動.比如在“對‘角’的不同定位”的案例中，學生運用所學知識求得∠CEB，就實現了第一層面的講題目的，這是常態講題教學的普遍性課堂現狀.而運用角色定位的方法引導學生思考“我是怎樣想的”“為什么這樣想”“思考過程中遇到哪些障礙”“如何突破障礙”“我還可以怎樣想”等等，讓其反復經歷高階思維活動，學會數學地思考，提高擬定方案的能力.因此，講題教學中，教師應明確角色定位的主旨要義，以更好地發揮講題教學效益.

4.2 角色定位的關注點

在日常講題教學中，我們會遇到兩種典型的教學困惑：一是教師認為明明講的很清楚、很到位，可學生不是太懂，仍然不能獨立正確解決問題；二是學生認為課堂上老師講的我都聽懂了，為什么接下來還是不會做題.要探索造成師生困惑的原因到底是什么，應著眼于教師教了什么和學生學了什么.講題教學的關鍵是培養學生的數學思維能力，特別是邏輯思維能力. 在講題教學中，以角色定位的視角關注題目、關注學生、關注方法，能有效培養學生的邏輯思維能力，實現深度學習，解決教學困惑.

(1)關注題目

圖11

理解題目是教師實施講題教學的基礎.題目應該精心挑選，難易適中，本著有利于啟發學生思維，發展數學能力的原則，向學生呈現所謂的好問題.教師在理解題目的基礎上引導學生從熟悉題目到深入理解題目，搞清楚未知量、已知數據、條件等信息，為探尋解題思路做充分準備.教師還應圍繞題目挖掘潛在的教學價值，對于適切的題目，用角色定位的視角引導學生分析、探索，以幫助學生豐富問題解決的策略. 比如在圖11中，直線a∥b，點B在直線b上，AB⊥BC，若∠2=55°，則∠1=__________°. 這里的“∠1”具備“多角色”特征，教學中，基于角色定位的視角，引導學生感受把∠1定位成內錯角或余角，決定不一樣的解題路徑，通過簡單的問題，引導學生學會多角度、靈活地思考問題，對適用于角色定位特征的問題，嘗試角色定位分析的方法，體會角色定位的價值.

(2)關注學生

《義務教育數學課程標準(2011年版)》指出：有效的教學活動是學生學與教師教的統一，學生是學習的主體，教師是學習的組織者、引導者與合作者.[1]學生作為講題教學的受教對象，不是課堂教學的“配角”，而是課堂教學的“主角”.波利亞認為教師應順乎自然地幫助學生，教師應當把自己放在學生的位置上，他應當看到學生的情況，應當努力去理解學生心里在想些什么，然后提出一個問題或是指出一個步驟，而這正是學生自己原本應想到的.[2]角色定位作為一種探尋解題思路的方法，是對“學為中心”教學理念的踐行，是關注學生、凸顯學習主體地位的具體做法.

(3)關注方法

講題教學是一種常規的學教方式，學生的學與教師的教在題目的講解傳授過程中達成.在這個師生互動的過程中，題目的解決只是起點，而數學思維方法的歸納和提煉才是落腳點.眾所周知，實行啟發式教學有助于落實學生的主體地位和教師的主導作用.角色定位是教師實施啟發式教學的具體方式之一，教學中，基于角色定位視角的引導點撥，是對聯系、轉化、整合、綜合、分析等數學方法的集中梳理，是引導學生經歷真實性、高階性思維活動的過程，這樣的過程必將促使講題教學既有寬度，也有高度，更有深度.