數(shù)學(xué)表達(dá)也很關(guān)鍵

朱琴

[摘 要]小學(xué)數(shù)學(xué)教學(xué)中，為了將復(fù)雜的邏輯講明白，或者將一些概念揭示清楚，鑒于小學(xué)生的理解力和語(yǔ)言表達(dá)能力，只能采用通俗易懂、平實(shí)無(wú)華的語(yǔ)言，但是，簡(jiǎn)單的口語(yǔ)化表達(dá)并不代表在關(guān)鍵處可以含混不清，該咬文嚼字的地方還得咬文嚼字。

[關(guān)鍵詞]數(shù)學(xué)表達(dá); 嚴(yán)謹(jǐn);軸對(duì)稱(chēng);百分?jǐn)?shù)

[中圖分類(lèi)號(hào)] G623.5[文獻(xiàn)標(biāo)識(shí)碼] A[文章編號(hào)] 1007-9068（2019）29-0036-02

教師身處教學(xué)前沿，聽(tīng)課評(píng)課是家常便飯，也是日常必修課。通過(guò)聽(tīng)課評(píng)課，教師不僅能客觀探究教法和教育理念，互相取長(zhǎng)補(bǔ)短，而且可以積累真實(shí)的教學(xué)資料。教學(xué)是一門(mén)藝術(shù)，尤其是小學(xué)數(shù)學(xué)教學(xué)，教師的一點(diǎn)小毛病或者失誤，都會(huì)令課堂教學(xué)效果大打折扣，甚至?xí)?yán)重誤導(dǎo)學(xué)生。本文就兩個(gè)教學(xué)案例，談?wù)勑W(xué)數(shù)學(xué)教學(xué)中教師用語(yǔ)的嚴(yán)密性。

一、軸對(duì)稱(chēng)與對(duì)稱(chēng)

【案例1】軸對(duì)稱(chēng)圖形教學(xué)片段

師：讓我們乘上時(shí)光穿梭機(jī)，重新回顧什么是軸對(duì)稱(chēng)圖形。

生1：將圖形沿著一條線對(duì)折，如果能夠完全重合，那么這個(gè)圖形就是軸對(duì)稱(chēng)圖形。

師：回答正確，看來(lái)這位同學(xué)找到了過(guò)去的記憶，回答準(zhǔn)確無(wú)誤。

師：請(qǐng)舉例說(shuō)明哪些常見(jiàn)的圖形是軸對(duì)稱(chēng)圖形。

生2：長(zhǎng)方形、菱形。

生3：等腰三角形、正三角形。

生4：還有平行四邊形。

生5：不對(duì)，平行四邊形不是對(duì)稱(chēng)圖形。

師：為什么把平行四邊形排除在外？請(qǐng)做出解釋。

生5：因?yàn)榘凑蛰S對(duì)稱(chēng)圖形的定義，通過(guò)操作，發(fā)現(xiàn)平行四邊形對(duì)折后無(wú)法與自身重合。

師：這說(shuō)明“對(duì)折后能否重合”是判別一個(gè)圖形是否是軸對(duì)稱(chēng)圖形的重要依據(jù)。

解析：上述案例中，學(xué)生說(shuō)出了“對(duì)稱(chēng)圖形”和“重合”兩個(gè)重點(diǎn)詞語(yǔ)，雖然表述不夠流暢，但是教師還是給予充分的贊許。然而，教師描述概念時(shí)務(wù)必要嚴(yán)密，表述準(zhǔn)確，不能含糊其辭、模棱兩可，更不能存在邏輯語(yǔ)法上的漏洞。難道平行四邊形不是中心對(duì)稱(chēng)圖形嗎？平行四邊形屬于中心對(duì)稱(chēng)圖形，還是對(duì)稱(chēng)的，只是不是軸對(duì)稱(chēng)。這節(jié)課主講的是軸對(duì)稱(chēng)圖形，所以一字之差則天壤之別。涉及重要論斷時(shí)，切記要逐字逐句推敲，切不可閃爍其詞，否則會(huì)將命題“平行四邊形是對(duì)稱(chēng)圖形”判錯(cuò)。

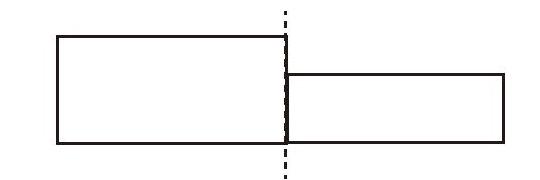
另外，軸對(duì)稱(chēng)圖形的定義也應(yīng)該嚴(yán)格陳述為“把一個(gè)圖形沿某條直線對(duì)折后兩邊完全重合，這樣的圖形稱(chēng)為軸對(duì)稱(chēng)圖形”。表述語(yǔ)中的關(guān)鍵詞“完全重合”至關(guān)重要，不可隨意刪減，否則就會(huì)產(chǎn)生歧義。如下圖所示，把該圖沿著虛線所在直線對(duì)折后左右兩邊也能重合，只不過(guò)是部分重合，沒(méi)有完全重合，所以嚴(yán)格來(lái)說(shuō)，它不是軸對(duì)稱(chēng)圖形，因?yàn)椴粷M足“完全重合”的要求。概念表述朦朧，造成的直接后果就似是而非。無(wú)怪乎總有教師反映，無(wú)論怎么強(qiáng)調(diào)學(xué)生就是無(wú)法正確甄別軸對(duì)稱(chēng)圖形，因?yàn)樵诟拍钸@一源頭上就走偏了。

二、百分?jǐn)?shù)

【案例2】百分?jǐn)?shù)練習(xí)課

在復(fù)習(xí)時(shí)，教師出示了填空題：“8千克比5千克多（），4毫升比5毫升少（）。”教師點(diǎn)名讓兩位學(xué)生上臺(tái)演算，并填空，其他學(xué)生獨(dú)立演算。上臺(tái)演示的兩位學(xué)生迅速算出結(jié)果，但是卻給出了截然不同的答案：3千克和20%。預(yù)設(shè)的答案應(yīng)該是60%和20%。面對(duì)這般結(jié)果，師生間進(jìn)行了如下交流：

師：這兩位同學(xué)的結(jié)果，你們認(rèn)可嗎？（學(xué)生中有的支持第一種結(jié)果，有的支持第二種結(jié)果，有的認(rèn)為兩種結(jié)果都正確）

師：這樣吧，我們整理一下大家的觀點(diǎn)。（經(jīng)統(tǒng)計(jì)，全班60人，有9人贊同第一種結(jié)果，有32人贊同第二種結(jié)果;教師讓大家圍繞兩種結(jié)果展開(kāi)討論。）

生1：我覺(jué)得兩個(gè)空都應(yīng)填寫(xiě)百分?jǐn)?shù)，目的是表示差量占單位“1”的比重。

生2：我反對(duì)，就字面意思，題目并未指明要填差量與單位“1”的關(guān)系，直接填寫(xiě)差額也說(shuō)得過(guò)去。

生3：第一個(gè)空應(yīng)填差值3千克就行，而第二空應(yīng)填寫(xiě)差額與標(biāo)準(zhǔn)值的比例20%。

……

（教師選取了幾個(gè)代表性意見(jiàn)進(jìn)行分析，同時(shí)提供權(quán)威解答，發(fā)表結(jié)論性結(jié)語(yǔ)。）

師：這節(jié)課的主題是百分?jǐn)?shù)的專(zhuān)項(xiàng)復(fù)習(xí)，所以要用百分?jǐn)?shù)解決問(wèn)題。

師：如果全部用百分?jǐn)?shù)解題，答案會(huì)是什么呢？

生4：第一個(gè)空的結(jié)果應(yīng)該是（8-5）∶5=60%，第二個(gè)空的結(jié)果應(yīng)該是（5-4）∶5=20%。

師：非常棒！通過(guò)這個(gè)練習(xí)題，我們鞏固了“求一個(gè)量比另一個(gè)量多（或少）百分之幾”的題型和計(jì)算方法……

解析：上述案例中，教師為了“推銷(xiāo)”自己的觀點(diǎn)而誤導(dǎo)了學(xué)生，最終學(xué)生被教師強(qiáng)行洗腦，接受了教師的觀點(diǎn)和結(jié)論。但是，知識(shí)是客觀的，“吾愛(ài)吾師，吾更愛(ài)真理”，求知摻不得半點(diǎn)水分，尤其是數(shù)學(xué)學(xué)科，往往一個(gè)關(guān)鍵詞或者引導(dǎo)語(yǔ)的失誤，或者表述有歧義，就會(huì)帶來(lái)思維混亂。

筆者認(rèn)為案例中的這道題，本就是低年級(jí)比較大小求差值的問(wèn)題，而并非求百分比的問(wèn)題。原題的大意應(yīng)該是：“8千克比5千克多幾千克？4毫升比5毫升少幾毫升？”若非要按教師的預(yù)設(shè)來(lái)回答，應(yīng)該對(duì)原題做一些改動(dòng)：“8千克比5千克多百分之幾？ 4毫升比5毫升少百分之幾？”題面中一定要寫(xiě)明求的是百分比，讓要求具體化，其實(shí)這也是分?jǐn)?shù)和百分?jǐn)?shù)應(yīng)用題的解題關(guān)鍵。條件或者問(wèn)題表述有歧義時(shí)，學(xué)生往往就會(huì)左右為難，難以決斷，結(jié)果就會(huì)出現(xiàn)很大的隨意性。

綜上可知，當(dāng)教師授課語(yǔ)言不夠精煉時(shí)應(yīng)該及時(shí)調(diào)整，數(shù)學(xué)有別于語(yǔ)文，語(yǔ)文里語(yǔ)義相近的詞可以互相替代，不影響閱讀與理解，但是數(shù)學(xué)卻說(shuō)一不二，近義詞所指代的具體內(nèi)容會(huì)有所差別，容易引起混淆。數(shù)學(xué)有它的嚴(yán)密性，一個(gè)概念往往由幾個(gè)關(guān)鍵詞共同定義，缺一不可。比如，倒數(shù)是相互依存的一對(duì)數(shù)，互為倒數(shù)關(guān)系的數(shù)絕不可以獨(dú)立存在。再如，對(duì)于“同圓或等圓中，圓的半徑都相等”，學(xué)生往往會(huì)忽略前提條件，直接抽取中心信息，得出結(jié)論“圓的半徑都相等”，從而出錯(cuò)。被忽略的前提條件，正是需要被強(qiáng)調(diào)的關(guān)鍵詞。教學(xué)中，教師要不斷通過(guò)舉一反三，讓學(xué)生深刻體會(huì)到數(shù)學(xué)表達(dá)的嚴(yán)密性，進(jìn)而重視數(shù)學(xué)表達(dá)。

[ 參 考 文 獻(xiàn) ]

[1] 方代新.多層促“說(shuō)”，提升學(xué)生數(shù)學(xué)語(yǔ)言表達(dá)能力[J].小學(xué)教學(xué)參考，2019（11）：86-87.

[2] 袁朦朦.學(xué)生表達(dá)能力在數(shù)學(xué)教學(xué)中的培養(yǎng)途徑[J].基礎(chǔ)教育論壇，2019（4）：40-41.

[3] 劉桂芳.淺談低年級(jí)計(jì)算教學(xué)中學(xué)生數(shù)學(xué)語(yǔ)言表達(dá)能力的培養(yǎng)[J].新教師，2018（12）：58-59.

（責(zé)編 羅 艷）