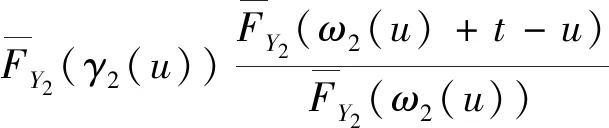溫貯備系統的隨機比較
伍 洋, 張正成, 溫九紅
(蘭州交通大學 數理學院,甘肅 蘭州 730070)
1 預備知識
在可靠性工程中,為提高系統可靠性,常用的方法是給系統貯備冗余元件,構成貯備系統,通常有三種貯備方式:熱貯備、冷貯備、溫貯備。熱貯備是指冗余元件在貯備狀態下的環境與其在工作狀態下的環境一樣,與工作元件構成并聯系統,因此在貯備狀態下,冗余元件可能會失效;冷貯備是指冗余元件在貯備狀態下不工作,失效率為零,當工作元件失效后,接替工作元件工作;溫貯備是指冗余元件在貯備狀態下處于一個相對溫和的環境中,失效率不為零,比其在工作狀態下的失效率小,當工作元件失效后,接替工作元件工作。許多學者對熱貯備、冷貯備已有了大量研究,如Boland等[1]利用隨機序討論了冷貯備元件在串聯(并聯)系統中的最優配置問題,Misra和Misra[2]研究了一個熱貯備元件在n中取k系統中的最優配置問題。近來,對溫貯備系統也有一些研究成果,如Ji等[3]推導出由兩個元件構成溫貯備系統的可靠度函數表達式,并討論了當元件服從指數分布時,溫貯備元件的最優配置條件,Li等[4][5]研究了一個或兩個溫貯備元件在串聯(并聯)系統中的最優配置問題,Hazra和Nanda[6]通過建立的三種模型,得到了溫貯備元件在串聯(并聯)系統中最優配置條件。
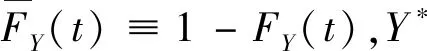
其中Yω(X)=[Y-ω(X)|Y>ω(X)],X|Y的可靠度函數為:
(1)
其中δ(u)=u-ω(u),u≥0,特別地當γ(t)=ω(t)≡0時,式(1.1)為冷貯備系統的可靠度函數,γ(t)=ω(t)≡t時,式(1.1)為熱貯備系統的可靠度函數。

2 主要結論
首先,利用隨機序比較兩個不同冗余元件分別與一個工作元件構成溫貯備系統的壽命。設隨機變量X為工作元件C的壽命,Y1,Y2分別為冗余元件R1,R2在正常工作環境下的壽命,比較以下兩個系統的壽命:T1=X|Y1和T2=X|Y2。
定理2.1如果元件滿足以下條件:(1)Y1hrY2,Y1或Y2為IFR;(2)對所有μ≥0,ω1(u)≥ω2(u),γ1(u)≥γ2(u),則T1stT2。
證明:根據式(1),對任意,t≥0,有
設Y1為IFR,因為Y1hrY2,ω1(u)≥ω2(u),則對所有0≤μ≤t
又γ1(u)≥γ2(u),則
那么
≥0。即證得T1stT2。
推論2.1假設ωi(u)=γi(u)(i=1,2),上述定理的條件“Y1或Y2為IFR”可省略。如果Y1stY2,對所有μ≥0,ω1(u)≥ω2(u),則T1stT2。
例2.1假設X,Y1,Y2服從參數為α,β1,β2的指數分布。如果Y1stY2,對所有μ≥0,γ1(u)≥γ2(u),則T1stT2。
證明:因為Y1stY2,γ1(u)≥γ2(u),所以
e-β2(t+γ2(u)-u)≥e-β1(t+γ1(u)-u),

考慮冗余元件在串聯系統中的最優配置的問題,設隨機變量X1,X2分別為工作元件C1,C2的壽命,Y1,Y2分別為冗余元件R1,R2在正常工作環境下的壽命,比較以下兩個系統的壽命:
T1=min(X1|Y1,X2)和T1=min(X1,X2|Y2)
Hazra和Nanda[6]推導出,若X1hrX2,Y2hrY1并且滿足以下任意條件之一:(1)對于u≥0,γ1(u)γ2(u)且ω1(u)=ω2(u);(2)Y1或Y2有對數凹(凸)生存函數,且對于u≥0,ω1(u)ω2(u)(ω1(u)≥ω2(u)),γ1(u)γ2(u),則T1≥stT2。若ωi(u)=γi(u)(i=1,2),上述條件“Y1或Y2有對數凹(凸)生存函數”可省略。
定理2.2如果X1hrX2,Y1≥stY2,且對所有μ≥0,ω1(u)ω2(u),則T1≥stT2。
證明:對任意t≥0,
因為Y1≥stY2,對所有μ≥0,ω1(u)ω2(u),則
又X1hrX2,則那么
即證得T1≥stT2。
例2.2假設X1,X2,Y1,Y2服從參數為α1,α2,β1,β2的指數分布。如果X1hrX2,Y1≥stY2且對所有的μ≥0,γ1(u)γ2(u),則T1≥stT2。
證明:對所有0≤μ≤t,因為Y1≥stY2,γ1(u)γ2(u)則e-β1(t+γ1(u)-u)≥e-β2(t+γ2(u)-u),又X1hrX2,所以α1≥α2,那么
即證得T1≥stT2。
定理2.3如果X1hrX2,Y1≥hrY2,且ω1(u)=ω2(u),γ1(u)=γ2(u),則T1≥stT2。
證明:對任意t≥0,
因為Y1≥hrY2,所以
又X1hrX2,所以即證得T1≥stT2。
考慮冗余元件在并聯系統中的最優配置,比較以下兩個系統的壽命:
T1=max(X1|Y1,X2)和T2=max(X1,X2|Y2)
定理2.4如果X1rhrX2,Y1hrY2,且滿足以下條件:
(1)Yi(i=1,2)是IFR;(2)對所有μ≥0,ω1(u)≥ω2(u),γ1(u)≥γ2(u),(i=1,2);(3)ωi(u)-γi(u)和u-ωi(u)(i=1,2)隨u≥0遞增,則T2≥stT1。
證明:對任意t≥0,
FT1(t)=P(max(X1|Y1,X2) 因為Y1hrY2,Y1是IFR,ω1(u)≥ω2(u),γ1(u)≥γ2(u),對所有0≤μ≤t, 因為X1rhrX2,所以FX2(t)FX1(u)-FX1(t)FX2(u)≥0,又Y2是IFR,ω2(u)-γ2(u)和u-ωi(u)(i=1,2)隨u≥0遞增,那么 推論2.2若ωi(u)=γi(u)(i=1,2),定理3.3中的條件“Yi(i=1,2)是IFR”可省略。如果Y1stY2,X1rhrX2,且對所有的μ≥0,ω1(u)≥ω2(u),u-ωi(u)(i=1,2)隨u遞增,則T1stT2。