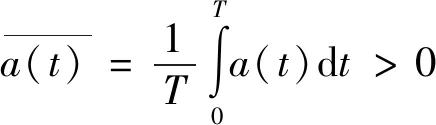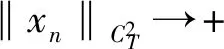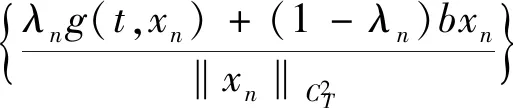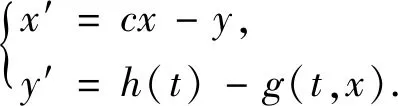On the Stability of Duffing Equations Using Lp Norms
LI Yu-chen, ZHANG Kang-qun
(Department of Mathematics and Physics,Nanjing Institute of Technology,Nanjing 211167,China)
Abstract:In this paper,the unique existence and local exponential asymptotic stability of a periodic solution of the second-order equations of Duffing type is proved.The sharp rate of exponential decay is determined for a solution that is near to the unique periodic solution.Furthermore,the positivity of such a periodic solution under an additional condition is obtained.
Key words:duffing equations;existence;stability;periodic solutions;positive solutions.
This paper is concerned with the existence,uniqueness and stability ofT-periodic solutions of the Duffing-type equation:
x″(t)+cx′(t)+g(t,x)=h(t),t∈[0,T]
(1)
x(0)=x(T),x′(0)=x′(T),
(2)
wherec>0 is a constant,h(t) is a continuousT-periodic function,g:[0,T]×R→Ris continuousL1-Caratheodory function (i.e.,for eachx,g(·,x) is measurable,for a.e.t∈[0,T],g(t,·) is continuous,for ?M>0,there exists a functionhM∈L1(0,T),such that |g(t,x)|hM(t) for |x|Mand a.e.t∈[0,T].),h(t) is a continuousT-periodic function.

instead of the original condition in [3]
where ‖φ‖d
Theorem 3.1 and Theorem 3.2 are the main theorems of this paper.Our paper is organized as follows.In section 1,we review some work about the Hill’s equation.In section 2,we deal with the homogeneous linear case,which is the start point of the homotopy invariance of topological degree.In section 3,we deal with the nonlinear case,using the theory of topological degree.
1 Preliminaries
In this section,let us review some work about the Hill’s equation
-u″+p(t)u=0,
(3)
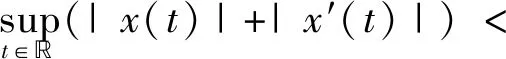
Assume thatp(t) is aT-periodic function in,andp(t)∈L1(),then consider the eigenvalue problem
Lu=-u″+p(t)u=λu
(4)
satisfying periodic boundary conditions
x(0)=x(T),x′(0)=x′(T)
(5)
or the anti-periodic boundary conditions
x(0)=-x(T),x′(0)=-x′(T).
(6)
The following conclusion about the eigenvalues and stability is well-known:

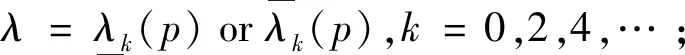

(3)equation (3) is stable ifλis in the intervals
(4)equation (3) is unstable ifλis in the intervals (-,
Next,consider the eigenvalues of (3) with the Dirichlet boundary condition:x(0)=x(T)=0.Then we have the following eigenvalues:
Moreover,it holds that the relation of the Dirichlet,periodic and anti-periodic eigenvalues as follows,for ?k∈N,
(7)
where,ps(t)≡p(t+s).
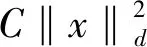
That is (see [9])
(8)
About the low bound of the first Dirichlet eigenvalue,we have the following result:
Lemma1.2[12]Letp(t)∈Ld(0,T) to be aT-periodic function,1dand
Using Lemma 1.2 and (7),it holds that
(9)
which will be used to prove the existence of a positive solution.
WithK(d),Zhang and Li[12] give the following result about the Hill’s equation(3):
Lemma1.3[12]Assume that for some 1d,p(t)∈Ld(0,T) is aT-periodic function such that1 WithK(d) and the upper-lower solution,Torres and Zhang[11] give the existence of the solution to the followingT-periodic boundary value problem(PBVP): x″+g(t,x)=0, (10) x(0)=-x(T),x′(0)=-x′(T). (11) whereg:[0,T]×R→Ris continuousL1-Caratheodory function.For upper solution,lower solution of (10),it means that Definition1.1A functionα∈C2(0,T)∩C1[0,T] is a lower solution of PBVP(10)-(11),if α″+g(t,α(t))≥0,a.e.t∈(0,T), α(0)=α(T),α′(0)≥α′(T). A functionβ∈C2(0,T)∩C1[0,T] is a upper solution of PBVP(10)-(11),if β″+g(t,β(t))0,a.e.t∈(0,T), β(0)=β(T),β′(0)β′(T). As an application of the anti-maximum principle,it holds that Lemma1.4[11]Letαandβbe a pair of reversed-order (i.e.,βα) lower and upper solutions of PBVP(10)-(11),and there exists a functionφ∈L1(0,T),φ>>0 such that g(t,v)-g(t,u)φ(t)(v-u) (12) for a.e.t∈[0,T] and ?u,v:β(t)uvα(t),then when ‖φ‖d In this section,we deal with the homogeneous linear case,which is the start point of the homotopy invariance of topological degree. Theorem2.1Consider the homogeneous linear PBVB x″+cx′+p(t)x=0, (13) x(0)=x(T),x′(0)=x′(T). (14) wherec>0 is a constant,p(t)∈L(R) is aT-periodic function satisfying (2)for somed∈[1,+],there existsφ∈L[0,T],‖φ‖d (15) By the condition (1),we have (16) (1)Existence.By (16),we can easily find a pair reversed-order constant upper and lower solutions of equation(15).In fact,?u≡-k<0 is a upper solution of equation(15),then ?u≡k>0 is a lower solution of equation(15) and they are reversed-order.By the mean value theorem,(16) satisfies obviously the condition(12) in Lemma 1.4,which gives the existence of aT-periodic solutionu(t) of equation(15). (2)Uniqueness.We proof it by contradiction.Suppose thatu(t),v(t) areT-periodic solutions of equation(15),thenz(t)=u(t)-v(t) is aT-periodic solution of Becausex(t)≡0 is aT-periodic of equation(13),by the existence and uniqueness,(13)has no nontrivialT-periodic solution,that is (13) only have vanishingT-periodic solution. (3)Rateofdecay.We obtain the rate of decay with the following two claims. Claim1:Equation(13) has no real Floquet multiplier. (17) u(t0)=u(t0+T)=0. (18) Forp(t)∈L(R) is aT-periodic function,multiplying (17) byuand integrating it holds that which contradicts the Poincaré inequality.Therefore (13) does not admit real multipliers. Consider the linear system X′(t)=A(t)X(t). (19) where, LetM(t) be a fundamental matrix solution of (19),by the Floquet theory,we haveM(t)=P(t)eBt,whereP(t),Bare all 2×2 matrices,P(t+T)=P(t),Bis a constant matrix. Letρ1=eTλ1,ρ2=eTλ2be the Floquet multipliers andλ1,λ2the corresponding Floquet exponents.Letx1,x2be the eigenvector components of the matrixeTB.It follows from claim 1 thatρ1andρ2are a pair of conjugates.Thus the eigenvectors associated with different eigenvalues are linearly independent.Thereforeyi=pi(t)eλit(fori=1,2) form the fundamental solution system of Equation(19).On the other hand,by applying the Jacobi-Liouville formula,we have The conclusions of nonlinear case will use theC1version of the Hartman-Grobman theorem as follows: Lemma3.1(Hartman-Grobman) Supposef∈C1(U?n→n),f(0)=0,such thatn→nis a contracting mapping.ThenfisC1conjugate equivalent to The following theorem is one of the main results: Theorem3.1(MainTheorem1) Consider the following PBVP: x″+cx′+g(t,x)=h(t), (20) x(0)=x(T),x′(0)=x′(T), (21) wherec>0 is a constant,h(t) is a continuous-periodic function,g:[0,T]×→is continuousL1-Caratheodoryexists and satisfies: for ?x∈and a.e.t∈[0,T]; (2)For somed∈[1,+],?φ∈L(),‖φ‖d for ?x∈and a.e.t∈[0,T]. Proof.The proof is similar to [3],but we should check every step carefully. (1)Existence.Consider the following parametrized equation φλ(x)=x″+cx′+λg(t,x)+(1-λ)bx=λh(t) (22) We claim that:?R∈,R>0, such that equation(22) has no solution on the boundary ?BRof the ball infor anyλ∈[0,1]. (23) So,it is pre-compact in the weak topology inL[0,T].Thus there are subsequences (also denoted by {xn}) such thatandλn→λ.Taking the limit in Equation(23) and assumezn(t)→z(t),one obtains that wherew(t)=λβ(t)+(1-λ)b.By the conditions,we have Noted that whenλ=0,the equationφ0(x)=x″+cx′+bx=0 has Next,by applying the homotopic invariance property,we have that deg(φ1,BR,0)=deg(φ0,BR,0)=1. This completes the proof of existence. (2)Uniqueness.We proof it by contradiction.Suppose thatx1(t),x2(t) are two differentT-periodic solutions of equation(20),thenu=x1-x2satisfies u″+cu′+p(t)u=0 (3)Rateofdecay.Consider the planar system associated with Equation(20), (24) LetX0(t)=(x0(t),y0(t)) be the uniqueT-periodic solution determined by the initial conditionX0(0)=(x0,y0).ThenX0corresponds to the unique fixed point of the Poincaré mappingPX=U(T,X),whereU(t,X) is the solution of (24) with initial valueU(0,X)=X.LetM(t) be the fundamental matrix solution of the linearization By the differentiability ofX(t) with respect to the initial value,the Poincare mapping can be expressed in terms of the initial valueXby the following formula: PX-X0=M(T)(X-X0)+o(X-X0). and we may suppose that forX-X0small,sinceφis near the identity.Therefore,the Lyapunov exponentμxis given by Remark.Whend=+,one has i.e.,‖φ‖is the same as Chen and Li[3]. By the Theorem 3.1,we can obtain the existence of a positive solution of (20)-(21).The following lemma is needed. Lemma3.2[10]Consider the Hill’s equation With this lemma,we have Proof.Take equation(20) into x″+cx′+p(t)x=h(t), Using (9),we have From Lemma 3.2 and Theorem 3.1,we complete the proof. Acknowledgement.The first author would like to express his gratitude to Professor Chen Hongbin,Xi’an Jiaotong University,for suggesting the problem and giving many instructions.2 Linear case


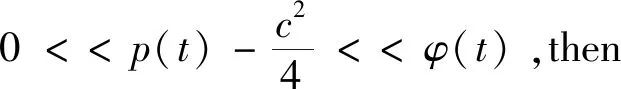
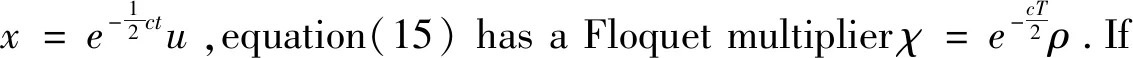
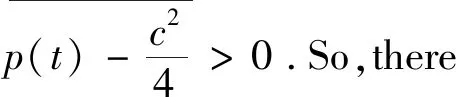


3 Nonlinear case