追本溯源，發(fā)現(xiàn)本質(zhì)
——對(duì)教材中橢圓一個(gè)定值問(wèn)題的深度探究與微拓展

廣東

潘巧玲

(作者單位：廣東省東莞市麻涌中學(xué))

在強(qiáng)調(diào)高考改革的今天，越來(lái)越多的高考試題呈現(xiàn)出回歸教材的趨勢(shì)，出題人通過(guò)改編、創(chuàng)新等手段賦予高考典型試題新的生命，這是高考命題的一種新走向.下面是筆者對(duì)教材中橢圓一個(gè)定值問(wèn)題的深度探究，并對(duì)試題進(jìn)行變式與微拓展，以引起各位同行重視.

一、探究背景

高考命題呈現(xiàn)出回歸教材的趨勢(shì)，回歸教材的目的就是要尋“源”.教材是很好的母題庫(kù)，每年高考試題中出現(xiàn)不少讓學(xué)生感到陌生的題目，實(shí)際上大多數(shù)高考題都是由教材例題或習(xí)題改編而來(lái)的，恰當(dāng)?shù)淖兪脚c微拓展可以幫助學(xué)生架起一座知識(shí)與知識(shí)之間的橋梁，讓學(xué)生在已知水平和未知水平之間自然過(guò)渡，但“萬(wàn)變不離其宗”，因此教師要引領(lǐng)學(xué)生在解決問(wèn)題后，進(jìn)一步挖掘其中的教學(xué)價(jià)值.深度探究也是讓學(xué)生建立充足的知識(shí)儲(chǔ)備的過(guò)程，在解題時(shí)就能得心應(yīng)手.下面是教材中橢圓的一個(gè)定值問(wèn)題.

題目1(人教A版選修4-4第15頁(yè)習(xí)題1.3第6題)已知橢圓的中心為O，長(zhǎng)軸、短軸的長(zhǎng)分別為2a,2b(a>b>0)，A,B分別為橢圓上的兩點(diǎn)，且OA⊥OB.

(2)求△AOB面積的最大值和最小值.

分析：在圓錐曲線(xiàn)中定點(diǎn)定值問(wèn)題是高考數(shù)學(xué)解析幾何類(lèi)試題考查的熱點(diǎn)問(wèn)題，其中定值問(wèn)題一般選擇坐標(biāo)法和參數(shù)法解題，利用圓錐曲線(xiàn)的性質(zhì)找等量關(guān)系.

二、探究過(guò)程

1.解法探究

試題解答：第(1)問(wèn)，

2.試題呈現(xiàn)

教材中的這個(gè)習(xí)題，不禁讓筆者想起了高三二輪復(fù)習(xí)中的一個(gè)模擬試題.

(1)求橢圓Ω的標(biāo)準(zhǔn)方程；

(2)設(shè)直線(xiàn)l′交橢圓Ω于C,D兩點(diǎn)，且OC⊥OD，求證：O到直線(xiàn)l′的距離為定值.

當(dāng)直線(xiàn)l′的斜率不存在時(shí)，設(shè)直線(xiàn)l′的方程為x=x0.

3.雙曲線(xiàn)中定值問(wèn)題的探究

橢圓和雙曲線(xiàn)在解析幾何中處于重要的地位，有很多類(lèi)似的性質(zhì)，兩者之間密切聯(lián)系，規(guī)律和諧，辯證統(tǒng)一.如果我們用類(lèi)比的方法去學(xué)習(xí)這兩部分的知識(shí)，可起到事半功倍的效果.有了以上兩個(gè)題目做基礎(chǔ)，我們發(fā)現(xiàn)橢圓中有的結(jié)論，雙曲線(xiàn)中也會(huì)有類(lèi)似的結(jié)論.

4.橢圓、雙曲線(xiàn)中定值的類(lèi)比

通過(guò)以上的證明，筆者發(fā)現(xiàn)題目1,題目2所出現(xiàn)的定值不是偶然，而是它們本身蘊(yùn)含的規(guī)律，于是有了以下結(jié)論：

從橢圓到雙曲線(xiàn)的類(lèi)比，將直觀想象、邏輯推理和數(shù)學(xué)運(yùn)算等數(shù)學(xué)核心素養(yǎng)融為一體，能有效地培養(yǎng)學(xué)生的邏輯思維能力、合情推理和探究能力.當(dāng)然類(lèi)比的結(jié)論不一定完全相同，也不一定適用，是否正確需要邏輯證明驗(yàn)證.

三、試題變式與微拓展

(1)求雙曲線(xiàn)的方程；

(1)求橢圓C的方程；

(2)斜率為定值k的直線(xiàn)l與橢圓C交于A、B兩點(diǎn)，且滿(mǎn)足|OA|2+|OB|2的值為常數(shù)(其中O為坐標(biāo)原點(diǎn)).

(ⅰ)求k的值以及這個(gè)常數(shù)；

(2)(ⅰ)設(shè)直線(xiàn)l的方程為y=kx+b,設(shè)A(x1,y1),B(x2,y2)，

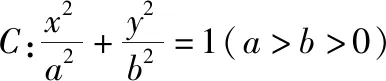
(1)求橢圓C的方程；

(2)證明：由題意可知直線(xiàn)l的斜率存在，且不為0.設(shè)直線(xiàn)l的方程為y=kx+b(b≠0)，點(diǎn)P,Q的坐標(biāo)設(shè)為P(x1,y1),Q(x2,y2)，令x=0可得y=b，即|NO|=|b|，

Δ=64k2b2-4(1+4k2)×4(b2-1)>0，即1+4k2-b2>0.

如果教師在課堂上僅處理橢圓與雙曲線(xiàn)的定值問(wèn)題就結(jié)束了，那么這道教材例題的價(jià)值就沒(méi)有被充分挖掘出來(lái).通過(guò)以上四個(gè)變式探究與微拓展，激發(fā)了學(xué)生探究數(shù)學(xué)的興趣和熱情，同時(shí)在探究的過(guò)程中，教會(huì)學(xué)生學(xué)會(huì)學(xué)習(xí)，學(xué)會(huì)發(fā)現(xiàn)問(wèn)題并解決問(wèn)題.通過(guò)變式教學(xué)，在探究問(wèn)題和解決問(wèn)題的過(guò)程中，調(diào)動(dòng)學(xué)生的積極性，培養(yǎng)學(xué)生的邏輯思維，加深同學(xué)們對(duì)知識(shí)的理解程度，進(jìn)一步把握知識(shí)的本質(zhì)與聯(lián)系.

四、教學(xué)反思

1.激活教材，融會(huì)貫通

通過(guò)對(duì)教材中橢圓一個(gè)定值問(wèn)題的深度探究，引出了多個(gè)變式拓展，通過(guò)變式再反思，又得到了很多結(jié)論.因此，筆者的感觸是，教材習(xí)題是值得挖掘的，而且是大有挖掘的價(jià)值，不要輕易放過(guò)教材中的任何一道題目，唯有以教材為本源，深度挖掘教材，靈活利用教材，才能讓高三復(fù)習(xí)真正“回歸教材”，才能溫故知新.教材的每道例題、習(xí)題都有它存在的價(jià)值，它們是專(zhuān)家經(jīng)驗(yàn)的積累，智慧的結(jié)晶，所以教師要學(xué)會(huì)引領(lǐng)學(xué)生做深度研究，教材永遠(yuǎn)是命題的本源，教會(huì)學(xué)生利用好教材，善于積累.總之，課堂教學(xué)要遵循以教材為主的原則，既沒(méi)有過(guò)時(shí)，更不能停留在口號(hào)上，如果教學(xué)中對(duì)例題的講解僅僅是照本宣科,忽視例題的典型示范作用,那么就不能讓學(xué)生體會(huì)到例題中蘊(yùn)含的解題思想和方法，因此教師可以通過(guò)改編教材習(xí)題中的某些條件或結(jié)論，得到解決一類(lèi)問(wèn)題的方法，從而充分發(fā)揮它們的教學(xué)功能.

2.重視探究，觸類(lèi)旁通