教學考試雜志社“優師計劃”階段性成果展示
——高考重難點相關試題選登

1.已知等差數列{an}的公差為2,S10=50,則a3+a6=

( )

A.0 B.2

C.4 D.6

【答案】D

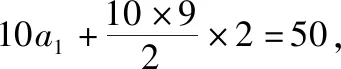
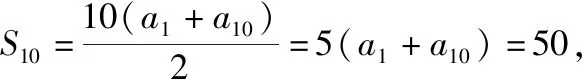
2.已知數列{an},{bn}的前n項和分別為Sn,Tn,且Sn=2n2+3n,2Tn=3bn-3,若兩個數列的公共項按原順序構成數列{cn},則c1=________,{cn}的前n項和Hn=________.(本題第一空2分,第二空3分)

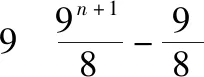
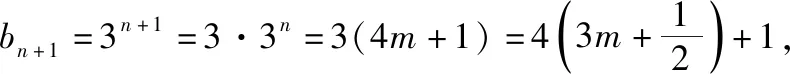
3.意大利數學家斐波那契在32歲時完成了自己的成名作《算盤全書》,58歲再版時增加了著名的“兔子繁殖問題”,即“斐波那契”數列問題,具體數列為1,1,2,3,5,8,…,即從該數列的第三項開始,每個數字等于前兩個相鄰數字之和.已知數列{an}為“斐波那契”數列,若a2020=t,則S=a1+a3+a5+…+a2019的值為

( )

A.t-1 B.tC.t+1 D.t+2

【答案】B

【解析】本題考查遞推數列以及數列求和，考查推理論證能力、化歸與轉化思想，考查邏輯推理、數學運算核心素養.由題意可得an+2=an+1+an,則a1+a3=a4，a1+a3+a5=a6,a1+a3+a5+a7=a8,……，a1+a3+a5+…+a2019=a2020=t,∴S=t,故選B.

【命題邏輯】數列是高中數學的重要內容，高考主要考查數列的概念以及等差數列、等比數列的概念、性質、通項公式與前n項和公式.其中，等差數列、等比數列的通項公式與求和公式是考查的重點.第一道試題的考查突出基礎性，重點考查考生對數列通性通法的理解和應用.而第二道試題為一道多空題，是2019年全國卷Ⅱ文理科首次出現的新題型，通過對題設進行巧妙的設計使其具有一定的綜合性，對基礎知識的考查和對能力的考查有機結合.試題通過運用等差數列、等比數列的定義推導通項公式，并以公共項構造新數列，重點考查考生對等差數列、等比數列相關知識的理解和掌握.更加考查學生的解題能力，體現了課程標準對數列教學的能力要求.第三道試題是以“斐波那契”數列為試題背景設計新型數列問題.本題重點關注對數學素養的考查，符合課標理念，同時引導考生關注“數學文化”，需要考生有比較強的閱讀抽象數學符號語言的能力和一定的邏輯推理論證能力.

( )

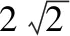
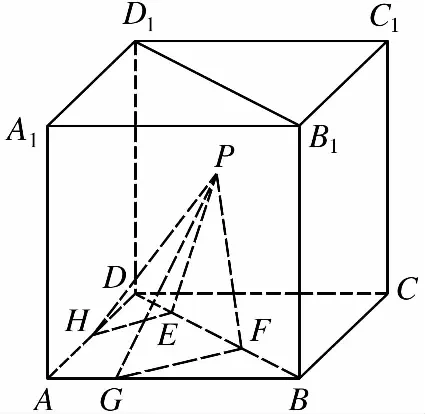
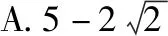
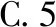
【答案】B

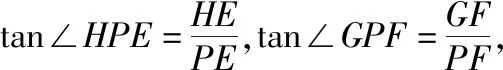
【命題邏輯】立體幾何是高中數學的重點內容，在立體幾何中，利用空間空間向量將幾何問題轉化為代數運算，是解決此類問題的一種重要的手段，試題的設計不是簡單的基本元素及相互關系，不僅關注了對基礎知識的考查，更重視了對數學能力的考查，試題的設計對考生的空間想象能力要求較高，綜合考查考生的空間想象能力、推理論證能力和運算求解能力.試題的設計源于教材且高于教材.