細品方知題真味
——2019年全國卷Ⅰ理科概率壓軸題的探究

廣東

林國紅

(作者單位：廣東省佛山市樂從中學)

2019年高考結束后，多數考生反饋全國卷Ⅰ理科數學的難度較高.其中最令人矚目的是第21題(解答題的壓軸題)，題目考查的是概率的內容，而將對概率的考查作為解答題的壓軸題，在近幾年高考全國卷中是史無前例的.由于此題字數較多，閱讀量大，情景陌生，而且除了考查概率的知識外，還綜合考查等比數列的證明與數列的其他相關知識，所以令考生望而生畏.本文將對此題進行解答分析，并進行深入探究，希望能起到拋磚引玉的效果.

一、題目呈現與解答

【題目】為治療某種疾病，研制了甲、乙兩種新藥，希望知道哪種新藥更有效，為此進行動物試驗.試驗方案如下：每一輪選取兩只白鼠對藥效進行對比試驗.對于兩只白鼠，隨機選一只施以甲藥，另一只施以乙藥.一輪的治療結果得出后，再安排下一輪試驗.當其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時，就停止試驗，并認為治愈只數多的藥更有效.為了方便描述問題，約定：對于每輪試驗，若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分，乙藥得-1分；若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分，甲藥得-1分；若都治愈或都未治愈則兩種藥均得0分.甲、乙兩種藥的治愈率分別記為α和β，一輪試驗中甲藥的得分記為X.

(Ⅰ)求X的分布列；

(Ⅱ)若甲藥、乙藥在試驗開始時都賦予4分，pi(i=0,1,…,8)表示“甲藥的累計得分為i時，最終認為甲藥比乙藥更有效”的概率，則p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…,7)，其中a=P(X=-1),b=P(X=0),c=P(X=1).假設α=0.5，β=0.8.

(ⅰ)證明：{pi+1-pi}(i=0,1,2,…,7)為等比數列；

(ⅱ)求p4，并根據p4的值解釋這種試驗方案的合理性.

【解答】(Ⅰ)X的所有可能取值為-1,0,1.于是P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β).

所以X的分布列為

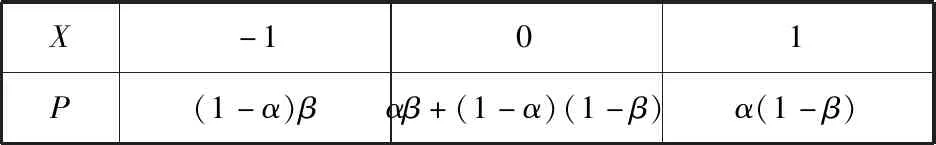
X-101P(1-α)βαβ+(1-α)(1-β)α(1-β)

(Ⅱ)(ⅰ)因為α=0.5，β=0.8，由(Ⅰ)得a=P(X=-1)=0.4,b=P(X=0)=0.5，c=P(X=1)=0.1.

因為pi=api-1+bpi+cpi+1，所以pi=0.4pi-1+0.5pi+0.1pi+1，故0.1(pi+1-pi)=0.4(pi-pi-1)，即pi+1-pi=4(pi-pi-1).

又因為p1-p0=p1≠0，所以{pi+1-pi}(i=0,1,2,…,7)為公比為4，首項為p1的等比數列.

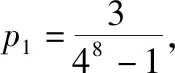
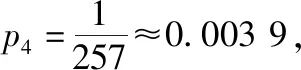
【評注】①問題(Ⅰ)只要正確理解題意，就能將其轉化為大家耳熟能詳的離散型隨機變量分布列，相對簡單.問題(Ⅱ)(ⅰ)中證明數列為等比數列，利用題目中已經給出的遞推公式和α=0.5，β=0.8這兩個條件，用到的是常規解法.問題(Ⅱ)(ⅱ)用大家熟悉的累加法求出等比數列通項公式，不難算出結果.最后根據概率極小說明試驗方案的合理性也是較為容易的.

②試題的解答方法是常規的，計算量也適中，這與教育部考試中心的“多考一點想的，少考一點算的”的命題精神相吻合.

③試題的難點是題目閱讀量較大，對學生造成了較大的負擔.會導致無法正確理解題意或者學生的運算出錯等失誤，另外試題放在最后壓軸題的位置出乎了考生意料，給考生造成了巨大的心理壓力.

二、解法優化

在上述解答中，問題(Ⅱ)(ⅱ)的做法是可以優化的，過程如下：

由(ⅰ)可知{pi+1-pi}(i=0,1,2,…,7)為公比為4，首項為p1的等比數列.所以可得pi+1-pi=4ip1.

從上面的解答過程，可以看出不用求出p1，同時p4的計算也得到了簡化.

三、問題(Ⅱ)的一般化

在解答完本題后，思考：若試題沒有給出α與β的數值，問題(Ⅱ)還能不能解答？如果能，p4如何表示？

答案是肯定的，解答的思路與過程跟原題解答類似.

因為a=P(X=-1)=(1-α)β，b=P(X=0)=αβ+(1-α)(1-β)，c=P(X=1)=α(1-β)，且pi=api-1+bpi+cpi+1.

所以pi=(1-α)βpi-1+[αβ+(1-α)(1-β)]pi+α(1-β)pi+1，

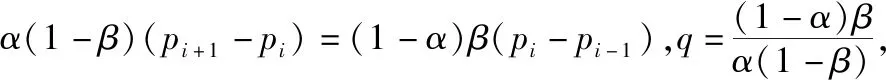
又因為p1-p0=p1≠0，所以{pi+1-pi}是以公比為q，首項為p1的等比數列，于是可得pi+1-pi=qip1.

顯然，當α=0.5，β=0.8時，q=4，這正是原試題的情形.

四、初始條件與遞推公式的由來

試題中所給出的初始條件p0=0，p8=1和遞推公式pi=api-1+bpi+cpi+1是否合理？能否根據題意推出初始條件和遞推公式呢？

事實上，是不需要給出初始條件和遞推公式的，這些可以根據題意推出來！

依題意知，當其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時，就停止試驗，并認為治愈白鼠只數多的藥更有效.甲藥、乙藥在試驗開始時都賦予4分，pi(i=0,1,…,8)表示“甲藥的累計得分為i時，最終認為甲藥比乙藥更有效”的概率，依照約定，可知每輪得分之和均為0，于是兩人得分之和始終不變，保持是8分.每多治愈一只白鼠則比對方多得2分，則若甲得0分，則乙得8分，故乙治愈的白鼠比甲多4只，實驗即可停止，故有p0=0，同理p8=1.

若甲得分為i，考慮下一輪，要么變為i-1，要么不變，要么變為i+1，其相應的概率恰為a,b,c.從而得到pi=api-1+bpi+cpi+1，其中a=P(X=-1),b=P(X=0),c=P(X=1).

所以試題完全可以不給初始條件p0=0，p8=1和遞推公式，試題把最難的求遞推公式部分直接給出來，實際是為了降低難度.而且問題(Ⅱ)(ⅰ)等比數列的證明其實也是可以不要的，之所以要證明等比數列也是為了降低難度，是命題老師給考生提示解題思路的.這樣做更好地控制了整道試題的難度，讓考生更容易解答.

當然如果試題不給初始條件和遞推公式，直接問最后一問，那樣試題的難度就大大提升了，而且在沒有提示的情況下作為高考題，也是違背全國卷的命題原則的，因為近年來全國卷一直堅持的原則是數列簡化，一般不考查由數列遞推公式經過復雜的變形求出數列通項公式的問題.如果要考查此類問題，一般會先證明一個輔助數列是等差或者等比數列，也就是像試題中那樣，所以此題中所涉及的數列內容是較常規的考查形式.

五、追本溯源

問“題”那得清如許，為有源頭活水來.原試題的題源來自于：

(2018年湖南省高中數學聯賽預賽B卷第12題)棋盤上標有第0,1,2,…,100站，棋子開始時位于第0站，棋手拋擲均勻硬幣走跳棋游戲.若擲出正面，棋子向前跳出一站；若擲出反面，棋子向前跳出兩站，直到跳到第99站(勝利大本營)或第100站(失敗大本營)時，游戲結束.設棋子跳到第n站的概率為pn.

(Ⅰ)求p3的值；

(Ⅲ)求p99，p100的值.

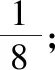
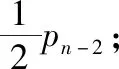
【評注】①高考題的問題(Ⅱ)與聯賽題的問題(Ⅱ)(Ⅲ)基本一致，聯賽題可以看作高考題的“題源”，高考題將本題進行適當的改編，賦予更豐富的命題背景，這說明命題專家很重視命題的傳承和相互借鑒.所以在高考的備考中，除了要進行高考真題的訓練外，還可以適當加入一些接近高考難度的高中數學聯賽題的訓練.

②對試題的探源，可以讓我們更深刻地認識問題，教師要善于鉆研高考題，用“慧眼”去發現有典型性、可拓展性的高考題，善于進行解后反思，方法的歸類，規律的總結與技巧的揣摩，再進一步對題目進行挖掘、拓展、延伸，擴大考題的輻射面，以此提高復習的效率.

六、試題的概率論背景

這道概率題是命題人站在隨機過程的馬爾可夫鏈(Markov Chain)角度命制的題目.馬爾可夫鏈，又稱離散時間馬爾可夫鏈，因俄國數學家安德烈·馬爾可夫得名，是狀態空間中經過從一個狀態到另一個狀態的轉換的隨機過程.該過程要求具備“無記憶”的性質：下一狀態的概率分布只能由當前狀態決定，在時間序列中它前面的事件均與之無關.這種特定類型的“無記憶性”稱作馬爾可夫性質.在馬爾可夫鏈的每一步，系統根據概率分布，可以從一個狀態變到另一個狀態，也可以保持當前狀態.狀態的改變叫做轉移，與不同的狀態改變相關的概率叫做轉移概率.下圖是一種最簡單的馬爾可夫鏈：隨機游走(Random Walk)的示意圖，這是概率論中著名的“直線上的隨機游走問題”.本試題相當于是隨機游走的一個變種，增加了一種分數維持不變的可能性.本題相當于有兩個邊界0和8，到達邊界后即停止，所以更準確地說是“有雙側吸收壁的直線上的隨機游走問題”.

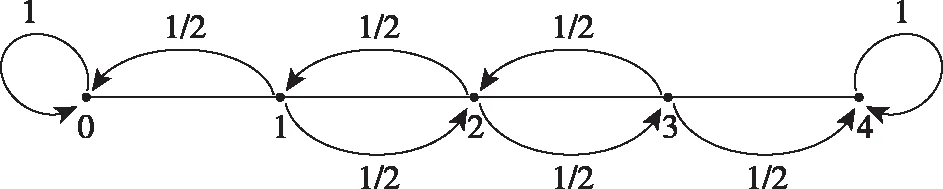
馬爾可夫鏈的本質較為簡單，就是一個事件之后的狀態只取決于上一步的狀態.例如在本試題中，第i+1次試驗之后兩種藥的分數，只會基于第i次試驗之后的分數+1/0/-1，所以之前的分數是多少就不需要知道，只知道第i次實驗之后的分數就足夠進行推測了.

題目中甲藥的分數就是這樣一個馬爾可夫鏈，而我們關心甲藥的分數和最后“試驗表明甲藥更有效”的概率之間的關系，這就要關系到甲藥在不同分數之間轉移的概率，就是題目中所給的遞推式：pi=api-1+bpi+cpi+1，這個關系式本質上表達了馬爾可夫鏈的傳遞規律，從pi由概率a傳遞到pi-1，由概率b留在pi，由概率c傳遞到pi+1.所以從pi出發，最終獲勝的概率也是如此傳遞的.給出這個關系式實質上大大降低了題目的難度，避免了考生因為不熟悉題目的背景而束手無策的問題.試題設計注重對問題背景的理解，將大學隨機過程的知識融在高中數列的角度中讓考生分析，本質上只需要高中數學的數列知識，而不需要復雜的計算工具.

馬爾可夫鏈是概率論中重要的一類問題，應用非常廣泛，有興趣的讀者可以查閱概率論的專業書籍進一步學習.

七、試題的啟示

近幾年全國卷Ⅰ的概率統計大題考查的知識點與背景不穩定，每年都有變化，例如2018年全國卷Ⅰ理科第20題結合了函數與導數，今年結合了數列.這種靈活多變的考題給考生的復習備考帶來了很多不確定性，也正是由于這種不確定性，對每位考生來說是最公平的.命題人教育理念新，專業知識精，選拔標準高，命制的試題超出一線教師的想象，但總能源于教材，高于教材，契合新課標的精神.

高考全國卷概率統計大題具有以能力立意、綜合性強和思維量大等特點，且實際背景新穎，對閱讀理解、推理分析和數據運算的要求較高，因此難度較大，但近兩年降低了運算的難度.統計背景下的概率題弱化計數問題，側重于統計思想，數據分析與處理，結合生活實際的決策性問題，突出數學的應用意識,突出學科素養導向，注重考查數學應用，體現綜合性和應用性的考查要求.試卷設置的情境真實、貼近生活，體現數學原理和方法在解決問題中的價值和作用.這有利于在中學數學教育中激發學生學習數學的熱情，提高學生對數學價值的認識，提升學生的數學素養，對中學的素質教育有很好的導向和促進作用.