初中數學幾何證明題的解題技巧芻議

周雪梅

摘 要：在初中數學學科中，幾何證明題作為一項基礎性的題目，是學生學習中的重點問題和難點問題，在初中數學教學課堂中，為了使學生可以具備較為完善的幾何證明題解題思路和解題方法，教師一定要向學生更多的講述一些幾何證明題的解題技巧，使學生可以對自身的解題思路進行不斷的反思和思考，提高學生的學習效率。

關鍵詞：初中數學;幾何證明題;解題技巧

在初中數學幾何證明題中，學生在解題的過程中有助于養成較為完善的邏輯思維能力，并且幾何證明題可以反映出學生的數學素養以及數學思維，因此在當前初中數學教育課堂中，幾何證明題的教學是非常重要的，教師應當從學生當前的學習需求和學習特征出發來對學生進行幾何證明題技巧的教學，使每個學生可以掌握相應的幾何證明題解題技巧，有效地提高學生解題的正確率。

一、初中幾何證明題基本思路

為了有效地提高學生解答幾何證明題的正確率，教師要在課堂教學中先向學生明確幾何證明題的解題思路，使每個學生可以按照正確的解題方向來進行幾何證明題的解答，從整體上看初中幾何證明題基本思路主要包括以下幾個方面：

（一）審題

在解答初中幾何證明題時審題是非常重要的，它不僅可以讓學生明確題目中已給的條件，也可以讓學生明確題目中各個條件之間的關系，因此教師要要求學生在進行幾何證明題解答的過程中一定要全面的審題，學生在拿到一道題目之后，一定要弄懂題目的要求、條件和作用，這樣才可以保證學生可以有序的開展后續的解題[1]。教師要要求學生在審題的過程中將已給的條件清晰地標出，對于一些容易犯錯誤的地方學生要值得注意。例如對于題目：“已知A、B、C三點在同一直線上，AB=10，AC=8，P和Q分別是AB、AC的中點，求PQ的長。”學生在審題的過程中，會有一部分學生審題不認真，誤認為C在AB上，這就造成了學生在后續解題的過程中經常會出現一些失誤，因此教師在初中數學教學課堂中向學生講述幾何證明題解題技巧時，一定要讓學生全面而認真的進行審題。

（二）標注

在對幾何證明題進行審題的過程中，標注也是非常重要的，教師要要求學生在審題時一定要弄清題目的題設和結論，并且要將題目中已知條件在圖形中進行標記這一步操作是非常重要的，教師在日常教學的過程中一定要向學生進行反復的強調[2]。例如在初中數學中，對于直角或者是等邊等角關系的證明題，直接在圖形上進行符號的標記，可以讓學生一目了然的明白題目中所給的條件。教師要要求學生在標記完成之后，要根據自身的數學基礎來進行題目的解答，這樣一來每個學生都會形成較為完善而清晰的解題思路，學生的解題正確率也會得到大幅度的提高。

（三）引申

在初中階段的幾何證明題中，有一部分的題型難度是比較大的，并且許多條件都隱藏在題目中，需要學生根據自身的數學基礎來進行解答，對于這種題目在解題的過程中需要學生學會引申，就是從所給的條件引申到所需的條件中，從而完成整個證明過程[3]。在解答這一類題型時，不僅要讓學生掌握基本的知識點，并且學生還要有一定的空間想象能力，教師要要求學生在審題的過程中要做好標注，并且要讓學生思考從這些隱藏條件中可以想到哪些結論，在學生思考完成之后，要在圖中進行標注。例如對于下圖中的題目：如圖△ABC的外角，∠BCD角平分線CE與∠BAC角平分線AE交于點E，若∠CBE=80°，則∠ACE=

對于這道題目的解答，難度是比較大的，大部分學生在解答的過程中經常會出現諸多的問題，這時教師要對學生的解題思路進行全面的引導，教師可以讓學生以E為△ABC的旁心，并且運用：三角形一內角與一外角的角平分線的交點，其夾角等于第三個內角的一半的理論。教師要讓學生在解答的過程中運用這一定理來進行解答，當學生運用這一定義進行解答時會發現整個問題是非常簡單的，學生遇到難題也會迎刃而解。

二、解題思路的總結

（一）基本圖形

在初中幾何題中，基本圖形的題型主要是為了反映概念和定理，這是學生進行初中幾何證明題解答的基礎步驟，在利用基本圖形進行解答時，可以幫助學生從一些復雜的圖形中找出解題思路，另外也可以幫助學生更快的發現添加輔助線的方法，因此教師在初中數學教學課堂中在向學生進行幾何證明題教學時，應當善于引導學生從一些復雜的圖形中分解出基本的圖形，并且要讓學生從已學的理論出發來進行實地的操作，之后，再由學生的實踐上升到更高層次的解答，從而使學生形成較為完善的解題思路。

（二）輔助線

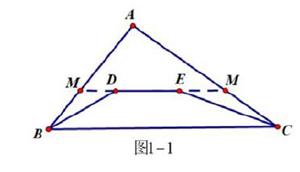
輔助線是學生在解答初中幾何證明題時必備的一項解題思路，輔助線的添加是幾何證明題的難點，因此教師應當在初中數學教學課堂中對學生進行幾何證明題教學時，應當對學生進行輔助線的教學，使每個學生可以掌握更多的畫輔助線的技巧，教師要告訴學生在畫輔助線時應當遵循化繁為簡的基本原則，通過輔助線的添加可以把一些不規則的圖形轉換為規則圖形，在畫輔助線時通常用于一些求圖面積的題型，例如最為常見的輔助線劃分方法是連接四邊形的對角線或者是平移對角線，輔助線是溝通命題中已知和求證結論的橋梁，因此掌握正確添加輔助線的方法是非常重要的。例如對于這道題：已知如圖1-1：D、E為△ABC內兩點，求證：AB+AC>BD+DE+CE.

學生在解答時可以按照這兩種思路來進行解題：證明：（法一）將DE兩邊延長分別交AB、AC 于M、N，

在△AMN中，AM+AN > MD+DE+NE;（1）

在△BDM中，MB+MD>BD; （2）

在△CEN中，CN+NE>CE; （3）

由（1）+（2）+（3）得：

AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE

∴AB+AC>BD+DE+EC

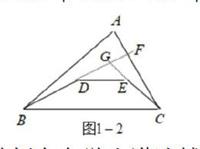
或者是通過這種方法來進行解答：如圖1-2， 延長BD交 AC于F，延長CE交BF于G，

在△ABF和△GFC和△GDE中有：

AB+AF> BD+DG+GF （三角形兩邊之和大于第三邊）（1）

GF+FC>GE+CE（同上）………（2）

DG+GE>DE（同上）……………（3）

由（1）+（2）+（3）得：

AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE

∴AB+AC>BD+DE+EC。

教師在向學生講述輔助線的做法時，應當根據一個題目來為學生進行有效的擴展，教師要要求學生在畫輔助線時，應當仔細的觀察題目中的要求，并且要運用自身的分析能力來轉化題干中的內容，結合重要的知識點來進行問題的轉化，創設由已知條件向所求結論的過渡，使得一些復雜的幾何問題得以解決。值得注意的是教師要告訴學生在畫輔助線時，并不是簡單的在平面圖形上亂貼亂畫，而是需要學生提前根據題目中所給的內容和要求來進行條件的創造，從而可以快速的得出問題的結論，教師要鼓勵學生在進行幾何證明題解答的過程中，應當根據自身的數學基礎來對輔助線的添加進行大膽的設想。

結束語

在初中數學教學課堂中，教師一定要向學生講述一些幾何證明題的解題思路和解題技巧，使每個學生的空間想象能力和邏輯思維能力可以得到有效地提高，教師應當讓學生從圖形的規律和各種題型的解題思路出發，將一些未知的條件轉換為已知的結論，從而最大程度的提高學生解題的正確率。

參考文獻

[1]何曉明.初中生幾何證明題解題錯誤的解決對策[J].數理化解題研究，2017（11）：21-25.

[2]朱毅剛.初中數學幾何證明的解題思維培養路徑探析[J].理科考試研究，2016（6）：26-30.

[3]葛敏潔.初中數學幾何證明題思路探析[J].數學教學通訊，2018（5）：120-123.