最值問題
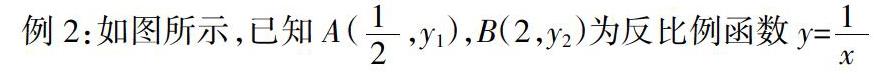
【學情分析】
本節課是在教材七年級上冊軸對稱的基礎上學習的,對于初四的學生已經掌握了所有知識,可以將特殊三角形、特殊四邊形、圓、一次函數、二次函數以及軸對稱、相似三角形等重要知識聯系在一起,本節課具有較強的靈活性、創新性和挑戰性,是中考中常考題型,常出現在中考壓軸題中,對于學生學習是個難點,需要經過小組學習,總結歸納此類問題解決的途徑。
【復習目標】
1.能利用軸對稱解決簡單的最短路徑問題,三角形三邊關系,提高學生運用數形結合、函數、建模等思想解決問題的能力,培養學生邏輯推理、運算和分題問題等核心素養。
2.體會圖形的變化在解決最值問題中的作用。
【重點難點】
重點:利用軸對稱將最短路徑問題轉化為“兩點之間,線段最短”問題。
難點:如何利用軸對稱將最短路徑問題轉化為線段和、差最小問題。
【學習過程】
自學展示:(學生獨立完成,找學生簡單講解)
1.點A、B在直線L的兩側,在直線L上找一點P使點P到A、B的距離之和最小。
2.直線L表示草原上的一條河流,一騎馬將軍從A地出發,去河邊讓馬飲水,然后返回位于B地的駐地,他應沿怎樣的路線行走,使路程最短?請作出這條最短路線。
3.線段AB=5,以B點為圓心,以2為半徑作圓,在圓上找一點C,(1)使AC1最小,(2)使AC2最大。
學生獨立完成,舉手搶答。
跟蹤訓練:(學生獨立完成,教師提問)
1.正方形ABCD,AB邊上有一點E,AE=3,EB=1,在AC上有一點P,使EP+BP為最短。求:最短距離EP+BP。
答案:連接DE,因為B、D關于AC對稱,所以EP+BP=DE,在Rt△ADE中AE=3,AD=3+1=4,所以EP+BP=DE=5。
2.在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小。
小組答疑(小組討論,找代表講解)。
例1:已知,A是銳角∠MON內部任意一點,在∠MON的兩邊OM,ON上各取一點B,C,組成三角形,使△ABC周長最小。
變式提升:兩個動點求最值。
3.∠AOB=30°,點M、N分別在邊OA、OB上,且OM=1,ON=3,點P、Q分別在邊OB、OA上,則MP+PQ+QN的最小值是多少?
出示答案:找學生講解
知識拓展:轉化“三角形兩邊之差小于第三邊(學生用幾何畫板展示動點P的運動路徑,得出結論,找學生講解)。
例2:如圖所
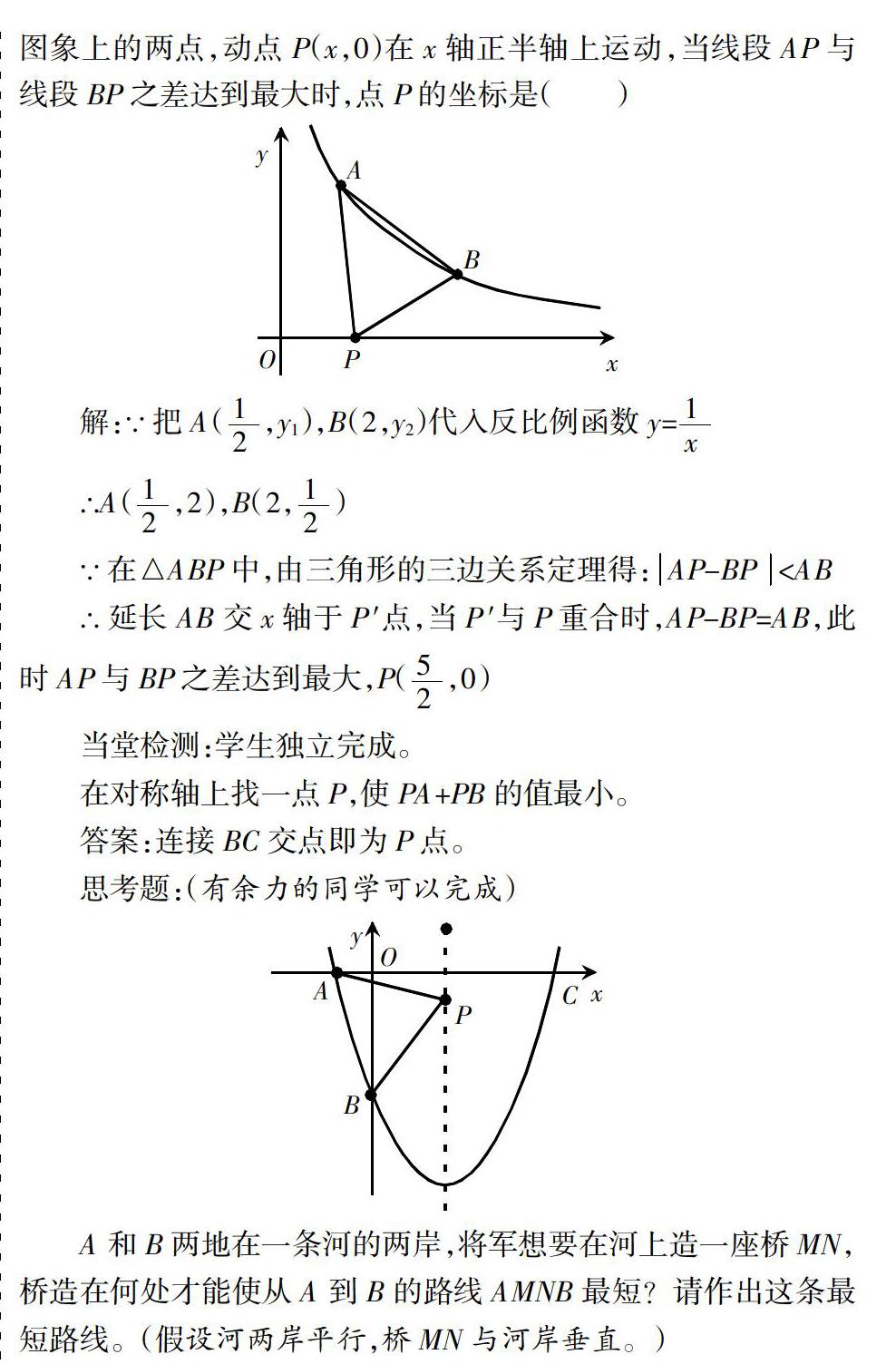
∵在△ABP中,由三角形的三邊關系定理得:AP-BP ∴延長AB交x軸于P ′點,當P ′與P重合時,AP-BP=AB,此時AP與B) 當堂檢測:學生獨立完成。 在對稱軸上找一點P,使PA+PB的值最小。 答案:連接BC交點即為P點。 思考題:(有余力的同學可以完成) A和B兩地在一條河的兩岸,將軍想要在河上造一座橋MN,橋造在何處才能使從A到B的路線AMNB最短?請作出這條最短路線。(假設河兩岸平行,橋MN與河岸垂直。) 教學設計說明: 先讓學生了解本節課的思想方法,使學生能很快切入主題。 思想方法: 一般地,解決線段和差最值問題的目標是“化曲為直”,手段通常是遇“和”轉化為異側,遇“差”轉化為“同側”,根據是軸對稱和全等三角形,常用方法是利用軸對稱圖形中的“已知”的對稱點。涉及的知識點有“兩點之間線段最短”“垂線段最短”“三角形三邊關系”“軸對稱”“平移”等。 在了解思想方法的基礎上出示前測,由學生獨立完成,本題是“馬飲水問題”的實際應用,考查了學生垂直平分線基本性質的理解與應用,起點低,難度不大。但作為教材中出現的習題都具有典型性、可遷移性,看似簡單的題目中包含“兩點之間,線段最短”“作一個點關于直線的對稱點”知識點,“折”轉“直”的轉化思想。 作者簡介:張雪梅(1979—),漢,黑龍江省綏化市,本科,中學二級,研究方向:數學課堂教學。

