剪刀式折疊橋梁架設軌跡規劃

張 帥，涂群章，韓 軍，朱鵬程，楊 旋

(1.陸軍工程大學 野戰工程學院， 南京 210007; 2.陸軍研究院 5所， 江蘇 無錫 214035)

某型剪刀式折疊橋樣機在當前架橋過程中主要采用人工操作電控系統依次驅動油缸動作的方式進行橋節的展開，人工展開主要憑借操作手的經驗，精度不高。采用油缸依次動作的方式，展橋過程中，每個油缸會出現多次啟停的情況，由于橋節質量大，慣性大，易形成較大沖擊。這與樣機實測過程中，電控系統控制油路打開和關閉時，折疊橋發生明顯的前后晃動現象相吻合，增加了展橋過程的不穩定因素。同時折疊橋的橋節跨度大且為三折結構，不合理的展開方案容易發生橋節之間干涉和橋節與地面碰撞的情況。軍用橋梁的展橋速度作為其性能的一項重要指標[1,2]。針對展橋過程進行展開次序設計和控制端點的軌跡設計，可以實現折疊橋按照規劃軌跡的快速安全展開。

黎暉等[3]按照折疊橋展橋過程中重心最低原則，研究了一種兩折剪刀式橋展開軌跡規劃，得到了規劃路徑展開時驅動油缸動作與控制端點位姿的映射關系，并且對不同展開步驟轉換處利用三次樣條曲線進行插值平滑處理，以達到減小沖擊的目的。Wang Xiaobang等[4]對一種大型線纜鏟車在挖掘過程中鏟斗端點軌跡進行了規劃，達到最小能量消耗的目的。石文凱等[5]對一種加油機器人操作臂進行了軌跡規劃研究。呂亞輝等[6]利用手持設備獲取軌跡路徑，進行工業機器人軌跡規劃。滕儒民等[7]利用啟發式路徑搜索進行高空作業車避障軌跡規劃。

本文首先利用運動鏈環路理論[8-9]進行了折疊橋機構的分析，建立了折疊橋運動學正反解模型。對于架橋兩岸存在不同的正負坡情況，以及兩岸之間存在凸起障礙，設置了坡度角φ，規劃了包含坡度角φ的端點運動軌跡模型，使得規劃軌跡對于不同坡度角具有通用性。設置了安全距離S0，保證橋梁在規劃軌跡進行展開過程，橋梁架設的安全。為了避免展橋過程中縱向過高產生的展橋迎風面積過大，折疊橋的抗風能力下降的情況，按照最低安全路徑原則進行展橋的軌跡規劃。采用了分步的展開方案的設計，規劃了折疊橋控制端點的運動軌跡，避免展橋過程中折疊橋不同橋節之間發生干涉，折疊橋與地面之間發生的碰撞，通過折疊橋的運動學反解模型得到了展橋機構的關節空間和驅動空間的協同動作序列。

1 剪刀式折疊橋運動學分析

1.1 機構的描述

新型剪刀式折疊橋構機構示意圖如圖1所示，包括第一橋節、第二橋節、第三橋節、連桿1、展橋架1、展橋油缸1、連桿2、展橋架2、展橋油缸2。支腿用于支撐展橋進行橋跨的展開，展橋過程中固定不動相當于機架，舌形臂油缸用于展橋的收放。各個部件通過鉸接進行約束，具有一個平面轉動的自由度。舌形臂油缸一端鉸接在支腿上A點，另一端與第一橋節鉸接于B點；第一橋節與支腿鉸接于o0點，第一，二橋節之間通過點o1進行鉸接；展橋油缸1一端鉸接于第二橋節G點，另一端鉸接于展橋架1上F點；連桿1一端與第一橋節鉸接于C點，一端與展橋架1鉸接于D點；第二橋節與展橋架1鉸接于E點；第二，三橋節之間的鉸接情況于第一，二橋節之間展橋機構完全相同，對稱分布[10]。

根據運動鏈環路理論建立折疊橋機構運動學模型，其簡圖如圖2，其運動鏈環路圖如圖3。根據Grübler-Kutzbach 修正公式[11]計算折疊橋的自由度

(1)

式中:M表示機構的自由度；d表示機構的階數；n表示構件數目；g表示運動副數目；fi表示第i個運動副自由度。

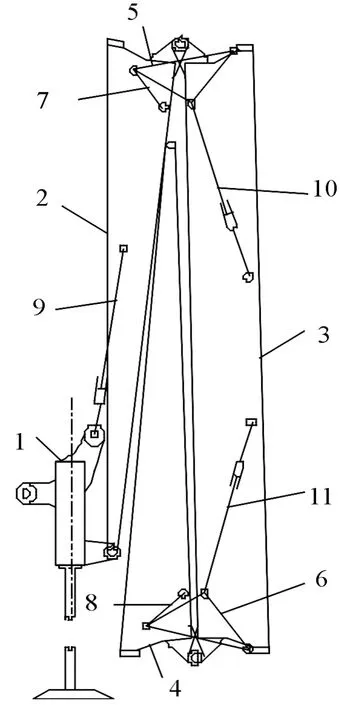
1.支腿，2.第一橋節，3.第二橋節，4.第三橋節，5.展橋架1，6.展橋架2，7.連桿1，8.連桿2，9.舌形臂油缸，10.展橋油缸1，11.展橋油缸2

圖1 新型剪刀式折疊橋機構示意圖

圖2 機構運動學模型簡圖

圖3 運動鏈環路圖

該平面機構階數為3，各個運動副都為單自由度，計算得該型剪刀式折疊橋在展橋過程中的自由度為3。

1.2 機構運動學分析

圖4中，S0表示安全距離，S1為坐標原點與地面的豎直距離，φ表示坡度角，直線a為展橋坡面，直線b為軌跡控制線，N為折疊橋上一控制端點。當選取變量不同時，折疊橋姿態可以分為不同的狀態空間，為了便于分析計算分別定義折疊橋驅動空間、關節空間、位姿空間[12]。驅動空間由舌形臂油缸的長度s1，展橋油缸1的長度s2，展橋油缸2的長度s3組成，可以表示為(s1,s2,s3)T。對于支腿、第一橋節、第二橋節和第三橋節組成的關節空間采用Denavit-Hartenberge法[13]建立相應的坐標系，可以表示為(θ1,θ2,θ3)T，其中θ1表示o0o1與xo軸正向所成角度，θ2表示o1o2與o0o1所成角度，θ3表示o2o3與o1o2所成角度。位姿空間由末端點的位置和姿態決定，可以表示為(x,y,ζ)T其中(x,y)T表示o3點在坐標系x0o0y0中的橫縱坐標，ζ表示o2o3與水平方向形成的夾角。利用運動學正解可建立驅動空間到關節空間再到位姿空間的關系，運動學反解可建立位姿空間到關節空間再到驅動空間的關系。

圖4 剪刀式折疊橋結構簡圖

1.3 運動學正解

運動學正解為給定三個油缸的尺寸，得到展橋機構末端點的位置姿態。在環路L1中給定舌形臂油缸尺寸s1，則該回路三個點的位姿可確定，進而關節空間中ο0ο1與x0軸之間的角度θ1可以確定；回路L3給定展橋油缸1的尺寸s2，則該回路三個點的相對位姿可確定，角度γ1可以確定；回路L2是有確定運動的平面四連桿機構，當γ1確定，則β3確定，整個環路的各點位姿可確定，ο1ο2與ο0ο1之間的關節角θ2可確定，同時L3中個點的絕對位置可以確定。回路L4中給定展橋油缸2尺寸s3，則回路三點的位姿可確定，φ1可得；回路L5為平面四連桿機構，當給定φ1,可得ψ1，則該回路各點位姿可以確定，ο2ο3與ο1ο2之間的關節角θ3可確定。由此可建立了驅動空間到關節空間的關系。

(2)

其中σ1是ο0A與x0軸正向之間的夾角，σ2是ο0B與ο0ο1之間的夾角。

(3)

β3=2π-γ1-σ3-σ4

(4)

其中:σ3為ED與EF之間的夾角，σ4為EG與Eo1之間的夾角，γ1為EF與EG之間的夾角，β3為ED與Eo1之間的夾角。

(5)

(6)

θ2=π-β2-σ5-σ6

(7)

其中:σ5為o1E與o1o2之間的夾角，σ6為o1o0與o1C之間的夾角，β2為o1E與o1C之間的夾角。

由于剪刀式折疊橋兩個展橋機構結構尺寸完全一致，s2與θ2的映射關系和s3與θ3的映射關系完全相同。

姿態空間與關節空間的對應關系，可以表示為

x=lo0o1cosθ1+lo1o2cos(θ1+θ2)+

lo2o3cos(θ1+θ2+θ3)+xo0

(8)

y=lo0o1sinθ1+lo1o2sin(θ1+θ2)+

lo2o3sin(θ1+θ2+θ3)+yo0

(9)

ζ=θ1+θ2+θ3

(10)

1.4 運動學反解

運動學反解是給定展橋機構末端的位置姿態求解三個驅動油缸的長度[14]。當給定o3點的位置和與xo0軸形成的夾角時，則鉸點o2的位置可以確定。

(11)

(12)

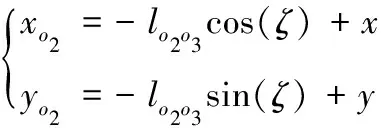
(13)

其中ζ為姿態角，對于非線性方程，利用Levenberg-Marquardt算法[11]求解方程(11)～(13)，可以得到關節空間角度值θ1、θ2，利用式(10)得到θ3。通過機構運動簡圖可以建立關節空間到驅動空間的關系[15]。已知ο0ο1與x0軸之間的角度θ1，則α2可得，回路L1中，舌形臂油缸長度s1可知；知ο1ο2與ο0ο1之間的關節角θ2，則β2可得，在回路L2中β3可得，在回路L3中γ1可得，進而得到展橋油缸1長度s2；知ο2ο3與ο1ο2之間的關節角θ3，則ψ2可得，在回路L5中ψ1可得，在回路L4中φ1可得，從而得到展橋油缸長度s3。

得到關節空間和驅動空間的關系如下：

(14)

β2=π-θ2-σ5-σ6

(15)

(16)

γ1=2π-β3-σ3-σ4

(17)

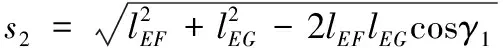
(18)

2 橋梁運動軌跡規劃

2.1 橋梁展開方案設計

剪刀式折疊橋展開方案設計如圖5所示。展橋準備時通過翻轉油缸(圖5未畫出)將折疊橋推至豎直狀態，接下來進行展橋作業。由于各橋節跨度大，且為三折結構，不合理的展開動作次序很容易造成展橋的干涉和展橋與地面的碰撞，因此架橋過程中，設計了各個油缸的展開次序以順利進行展橋操作。圖中P1、P2、P3、P4為第三橋節上N點在展橋過程中依次經過的空間點;Q1、Q2、Q3、Q4、為第三橋節上o3點在展橋過程中依次經過的空間點。P0，Q0為折疊橋處于豎直狀態時N點和o3點的空間位置。

圖5 剪刀式折疊橋展開方案設計示意圖

第1步：

為避免第三橋節與第一橋節發生干涉，此階段，展橋油缸2處于閉鎖狀態，舌形臂油缸和展橋油缸1協同動作，使得第三橋節上的控制端點N由起始空間點P0點展開到直線b上P1點，如圖5(a)所示，P1可以根據需要P0和P2范圍內進行選取。采用兩次函數規劃端點N在P0和P1點之間的軌跡，利用P0點，P1點的坐標和直線b的斜率確定展橋機構在P0和P1段的展開路徑。

P0到P1的軌跡曲線為

y=ax2+bx+c

(19)

其中

式中(xP0,yP0)、(xP1,yP1)分別表示P0點和P1點坐標。

根據二次函數規劃路徑，知N點的坐標xN,yN和角度θ3，進行關節空間和驅動空間的求解。首先將端點N點的坐標轉換成o3點的坐標

(20)

其中σ7為ο3N與ο3ο2之間的角度。

根據N點的坐標xN,yN以及關節角度θ3，利用式(10)～式(13)與式(20)可求得關節空間角度θ1、θ2以及姿態角ζ。利用式(14)～式(18)進一步可求得驅動空間油缸長度。

第2步：

當N點到達直線b上位置P1后，將沿著直線運動，直到θ2達到安全展開角度，此時N點在曲線上的位置為P2。端點N路徑為

y=xtanφ+d

(21)

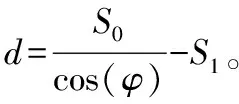
利用已知角度θ2，θ3值，代入式(10)～式(13)與式(21)可解出此時的P2點坐標位置。

此階段與第一階段的已知量相同，利用直線b上N點的坐標位置和角度θ3可以反解出展橋端點N沿著直線b進行展開時，對應的關節空間和驅動空間。

第3步：

此時N點從P2點開始沿著直線b繼續向前移動，展橋油缸2同步開始動作，進行第二，三橋節的展開，角度θ3開始變化，三個油缸協同動作，直到ο3N與直線b重合。此時o3點位于直線b上Q3點處，N點位于直線b上P3點處。P3點的坐標位置可以根據需要在一定范圍內進行選取。

使得姿態角ζ按照下列規律進行變化

(22)

其中ζQ3=φ-π+σ7；ζQ2，ζQ3分別表示Q2和Q3點處姿態角；xP2表示P2點橫坐標。

此階段N點的坐標位置由式(21)可得，進一步由式(20)得到o3點的坐標位置，結合姿態角ζ利用式(10)-(13)可以反解出關節空間，利用式(14)-(18)進一步反解得到驅動空間。

第四步：

當N點到達P3點，o3點到達Q3，將o3作為末端點考慮，此時展橋具有三個自由度，使得o3沿著直線b進行折疊橋的展開到Q4的位置，當給出姿態角隨著o3點的橫坐標變化規律，通過運動學反解，展橋的姿態可完全確定。由于當o3處于Q4位置時，θ2、θ3的值是確定的，利用式(10)～式(13)與式(20)可解出Q4的坐標。

使得姿態角ζ按照如下規律進行變化

(23)

式中ζQ4表示Q4點姿態角；xQ3表示Q3點橫坐標。

此階段利用o3點坐標以及姿態角ζ利用運動學反解可求得相應的關節空間和驅動空間。

3 橋梁運動軌跡分析

利用折疊橋的分步展開方案，可以快速得到油缸在仿真架設過程中的油缸行程協同變化，為展橋機構的控制系統提供指導。如圖6所示，利用運動學反解，分別得到舌形臂油缸、展橋油缸1和展橋油缸2在-5°、0°，5°坡度角情況下，端點軌跡按預定規劃軌跡展開時的油缸的協同變化情況。

圖6 不同姿態角情況下三個油缸協同變化

如圖7所示，取坡度角φ=5°，端點N和o3為作為軌跡規劃過程中的控制端點，通過運動學反解得到驅動空間三個油缸的協同變化情況，如圖6所示。將三個油缸協同動作序列代入運動學正解得到端點N和o3為軌跡，對比正反解情況下端點N和o3空間軌跡完全相同，可以驗證運動學正反解模型建立正確。

圖7 控制端點空間軌跡

圖8為坡度角φ=5°時，展橋過程中鉸點o1、o2和o3點的空間運動軌跡，根據折疊橋的結構特點，縱坐標的最大值近似反映了折疊橋豎直方向的高度。由圖8可得，在初始位置折疊橋豎直方向的高度最高，全局坐標系x0o0y0中y0坐標為3.146 m，其中S1為1.095 m，則橋身距離地面最高高度為4.241 m，展開過程中展橋的豎直高度小于初始位置。

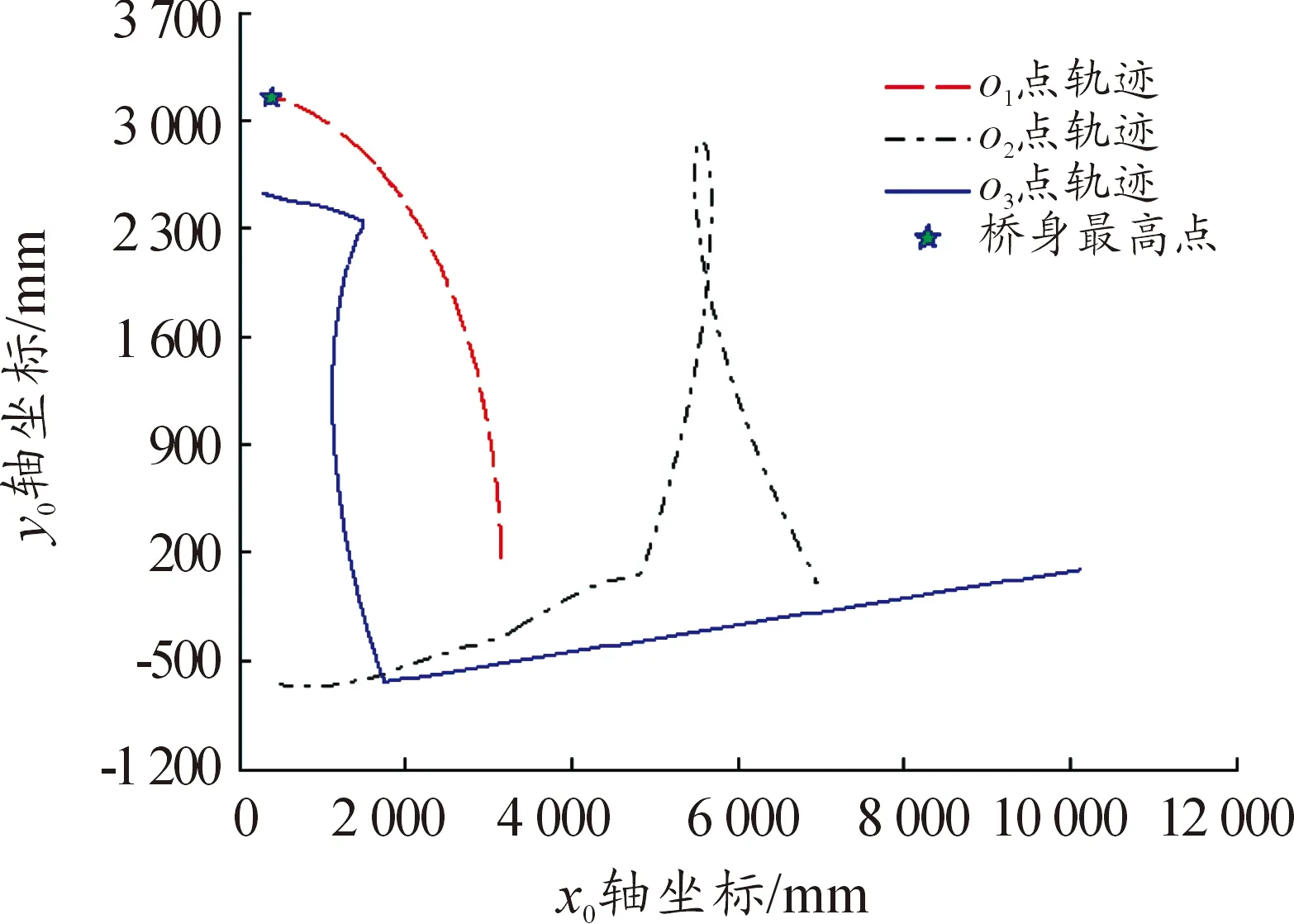
圖8 φ=5°時橋節點空間軌跡

由圖9所示，橋身最高點在坐標系x0o0y0中的縱坐標隨坡度角的變化規律。圖中可得在坡度角處于(-20°～20°)時橋身最高點距離o0點縱坐標最大值為4.291 m，距離地面最大距離為5.386 m。該軌跡規劃方法相對人工操縱油缸依次展開的方法，橋身在豎直方向高度大幅降低，可具有較好的抗風能力。

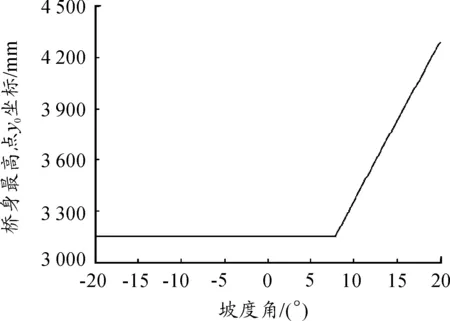
圖9 橋身最高點縱坐標隨坡度角的變化

4 結論

1) 針對一種新型折疊橋設計了其展開的軌跡規劃路徑，通過運動學反解快速得到不同坡度角情況下折疊橋油缸的協同變化曲線，指導油缸行程控制，實現折疊橋的快速展開。

2) 利用運動學正解，分析此軌跡規劃方法，使展開過程中折疊橋橋身的縱向高度較低時，仍具有較好的抗風能力。