EFP成型數(shù)值模擬及侵徹威力試驗(yàn)研究

白利紅，苗 成,2，武海玲，鐘 濤,2，周士猛,2，曾 晶

(1.中國(guó)兵器科學(xué)研究院 寧波分院， 山東 煙臺(tái) 264003； 2.沖擊環(huán)境材料技術(shù)重點(diǎn)實(shí)驗(yàn)室，山東 煙臺(tái) 264003； 3.山東特種工業(yè)集團(tuán)有限公司軍品研究所，山東 淄博 255201)

爆炸成型彈丸EFP(Explosive Formed Penetrator)戰(zhàn)斗部是一種具有高速度、大炸高等特點(diǎn)的介于穿甲彈和破甲彈之間的彈種，目前得到國(guó)際彈藥領(lǐng)域廣泛的重視和研究[1-2]。遠(yuǎn)距離作用彈藥(末敏彈、反直升機(jī)彈藥)要求EFP飛行距離在50～150 m，甚至更遠(yuǎn)[3]。這對(duì)EFP的氣動(dòng)外形、飛行穩(wěn)定性和威力提出了更高的要求，首先要求初速高、大質(zhì)量、初始動(dòng)能大，其次EFP具有較強(qiáng)的速度保持能力和較好的飛行穩(wěn)定性，最終保證EFP對(duì)目標(biāo)的命中和侵徹[4-7]。本文采用有限元分析軟件LS-DYNA，對(duì)EFP成型過(guò)程進(jìn)行數(shù)值模擬，通過(guò)靶試試驗(yàn)，測(cè)試EFP各距離處測(cè)速靶和天幕靶上的穿靶形態(tài)、速度和100 m處的侵徹威力，為EFP戰(zhàn)斗部的應(yīng)用和工程設(shè)計(jì)提供參考。

1 EFP成型數(shù)值模擬計(jì)算

1.1 仿真模型

EFP裝藥結(jié)構(gòu)主要由殼體、炸藥、藥型罩等部分組成。EFP裝藥結(jié)構(gòu)如圖1所示， D80 mm口徑紫銅球缺罩，裝藥為8701壓裝，裝藥高度為0.8倍裝藥口徑。

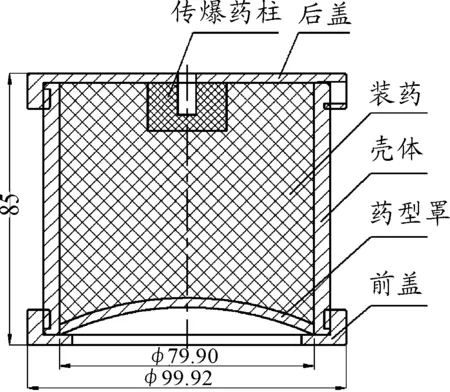
圖1 裝藥結(jié)構(gòu)示意圖

為了減少網(wǎng)格數(shù)量和計(jì)算時(shí)間，建立1/4實(shí)體三維模型，如圖2。基于LS-DYNA動(dòng)力學(xué)分析軟件，采用拉格朗日算法(Lagrange),自動(dòng)面面接觸。如此設(shè)計(jì)是由于拉格朗日算法建模相對(duì)歐拉(Euler)算法和任意拉格朗日-歐拉(ALE)算法，建模簡(jiǎn)單，且已能夠保證計(jì)算準(zhǔn)確性。

圖2 EFP仿真模型

1.2 材料本構(gòu)模型與參數(shù)

1.2.1炸藥本構(gòu)模型與參數(shù)

戰(zhàn)斗部裝藥采用MAT_HIGH_EXPLOSIVE_BURN(高能炸藥燃燒)材料模型，計(jì)算JWL炸藥爆轟產(chǎn)物壓力使用JWL狀態(tài)方程(1)：

(1)

式(1)中：A、B、R1、R2、ω為輸入?yún)?shù)；E為初始比內(nèi)能;DCJ為爆速;PCJ為CJ面的爆轟壓力。具體參數(shù)見表1。

表1 8701炸藥的爆轟性能參數(shù)及狀態(tài)方程參數(shù)

1.2.2藥型罩本構(gòu)模型與參數(shù)

藥型罩的材料模型為*MAT_STEINBERG，該模型反應(yīng)了高導(dǎo)無(wú)氧銅在高壓、高應(yīng)變率下本構(gòu)模型及狀態(tài)方程，其材料參數(shù)見表2。根據(jù)該模型理論，材料熔化前的剪切模量、屈服強(qiáng)度由式(2)～(3)確定。

(2)

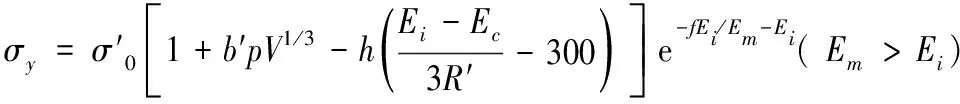
(3)

材料熔化之后，σy和G設(shè)置為初始值的一半。

表2 高導(dǎo)無(wú)氧銅材料參數(shù)

1.2.3殼體采用*MAT_JOHNSON_COOK模型

Johnson-Cook材料模型是一個(gè)能反映應(yīng)變率強(qiáng)化效應(yīng)和溫升軟化效應(yīng)的理想剛塑性強(qiáng)化模型。

(4)

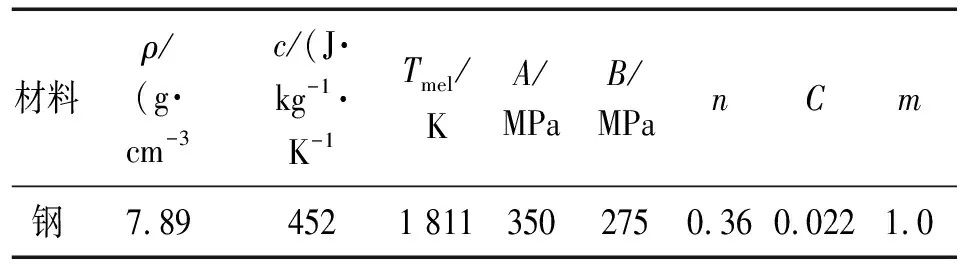
表3 殼體材料參數(shù)

1.3 仿真計(jì)算結(jié)果

圖3是EFP成型過(guò)程的數(shù)值模擬。裝藥起爆后球形爆轟波向藥型罩運(yùn)動(dòng)，20 μs時(shí)藥型罩頂部在爆轟波作用下開始沿軸線壓垮，52 μs時(shí)藥型罩頂部較底部較早飛出，可知頂部微元的軸向速度明顯大于底部微元的速度，同時(shí)彈丸邊緣向軸向方向靠攏，形成擴(kuò)展的尾部，可知邊緣處微元速度較附近沿徑向方向藥型罩微元速度大，此時(shí)EFP為向后翻轉(zhuǎn)成型模式。爆轟能量一部分用于加速藥型罩的運(yùn)動(dòng)，一部分用于藥型罩自身的塑性變形，在軸向拉伸和徑向壓縮作用下，200 μs時(shí)EFP完全成型為短桿狀。這種形狀有利于EFP的遠(yuǎn)距離飛行、侵徹威力高。

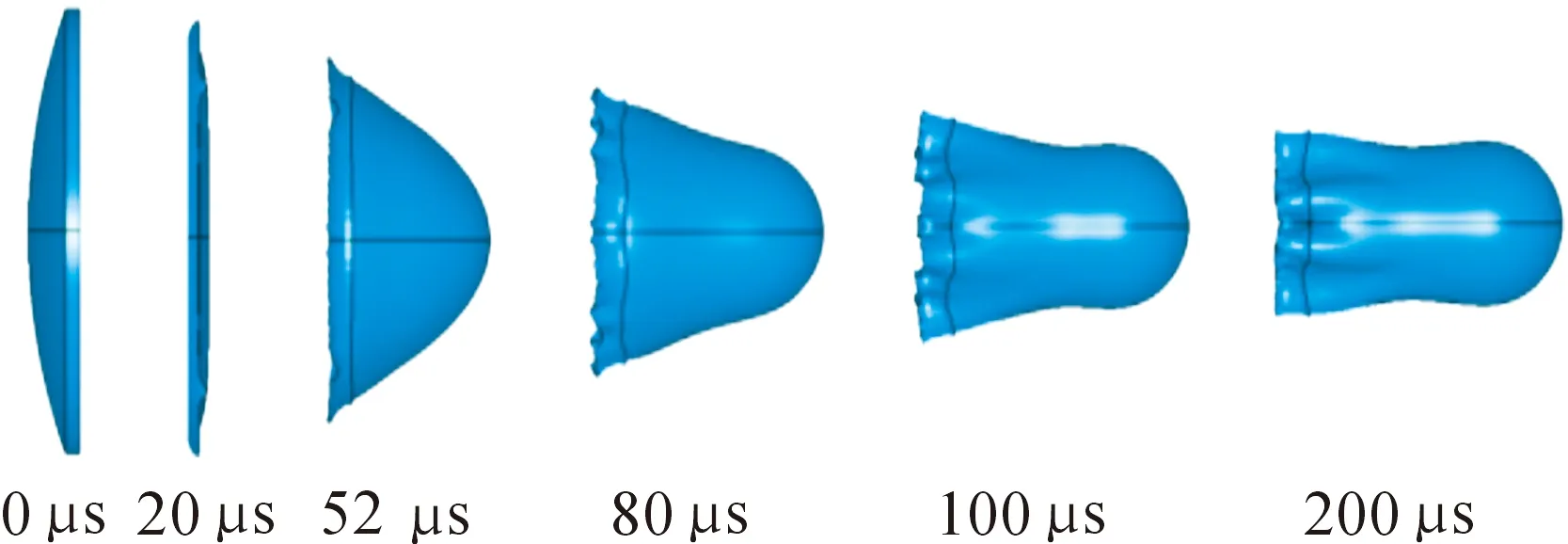
圖3 EFP成型過(guò)程

圖4是EFP的速度- 時(shí)間曲線，反映了EFP成型過(guò)程中速度的變化過(guò)程，可以對(duì)于EFP的速度變化有一個(gè)直觀的了解。由圖4可知，20～52 μs時(shí)速度急劇上升，此階段EFP處于成型初始階段，頭部和尾部還沒(méi)有完全成型；52～200 μs時(shí)EFP處于軸向拉伸和徑向壓縮階段，速度趨于穩(wěn)定，200 μs時(shí)EFP已完全成型，并在空氣中穩(wěn)定飛行，速度為2 100 m/s。

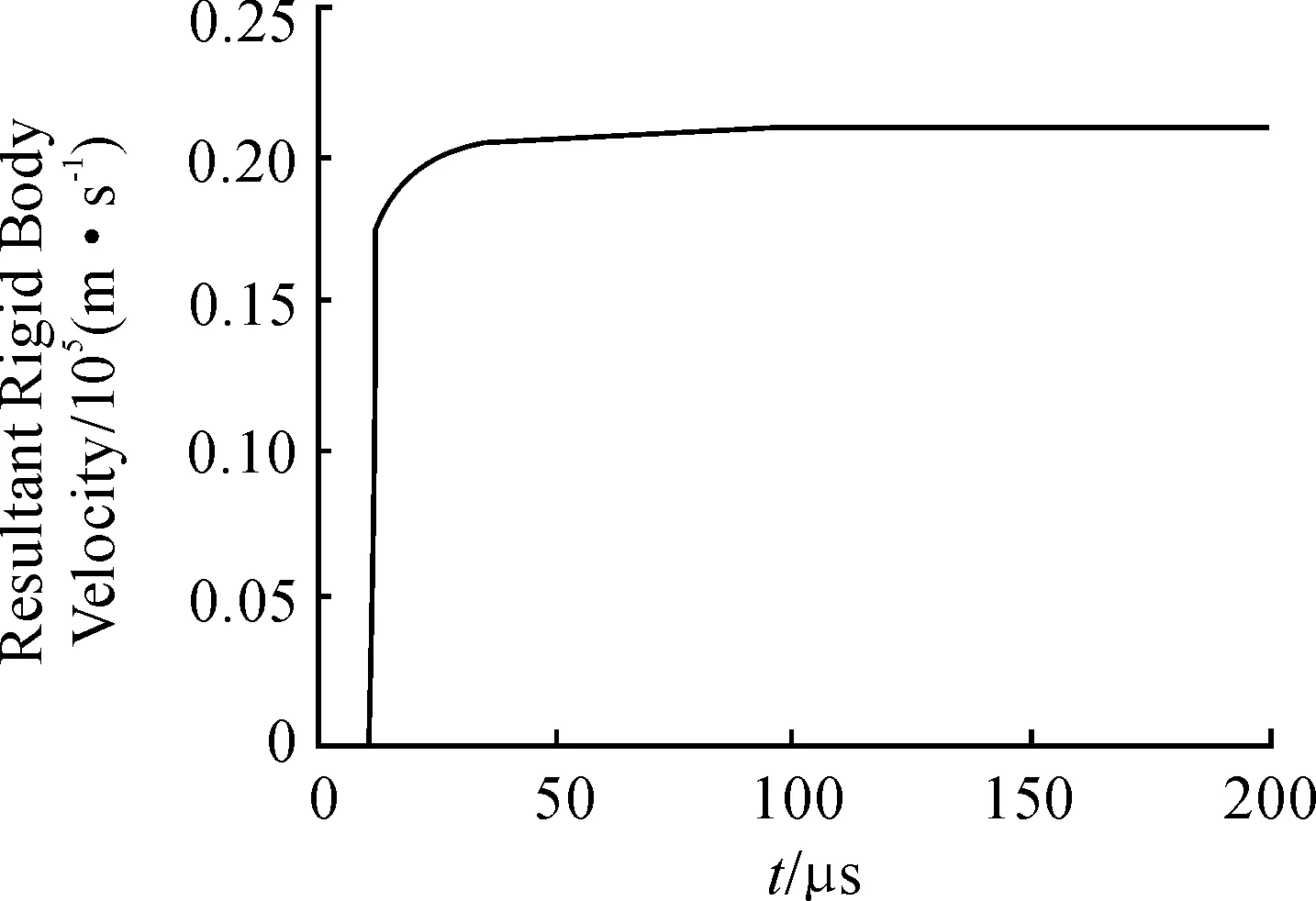
圖4 EFP速度-時(shí)間曲線

2 試驗(yàn)設(shè)計(jì)

試驗(yàn)所設(shè)計(jì)EFP裝藥結(jié)構(gòu)的材料及其尺寸參數(shù)與數(shù)值模擬一致，采用網(wǎng)靶記錄各距離處EFP的翻轉(zhuǎn)情況，根據(jù)各網(wǎng)靶留下的彈孔形狀判斷EFP的成型性，測(cè)速靶和天幕靶測(cè)各距離處EFP的速度。試驗(yàn)樣彈如圖5所示，試驗(yàn)現(xiàn)場(chǎng)布置見圖6，試驗(yàn)布置見圖7。

圖5 試驗(yàn)樣彈

圖6 試驗(yàn)現(xiàn)場(chǎng)布置

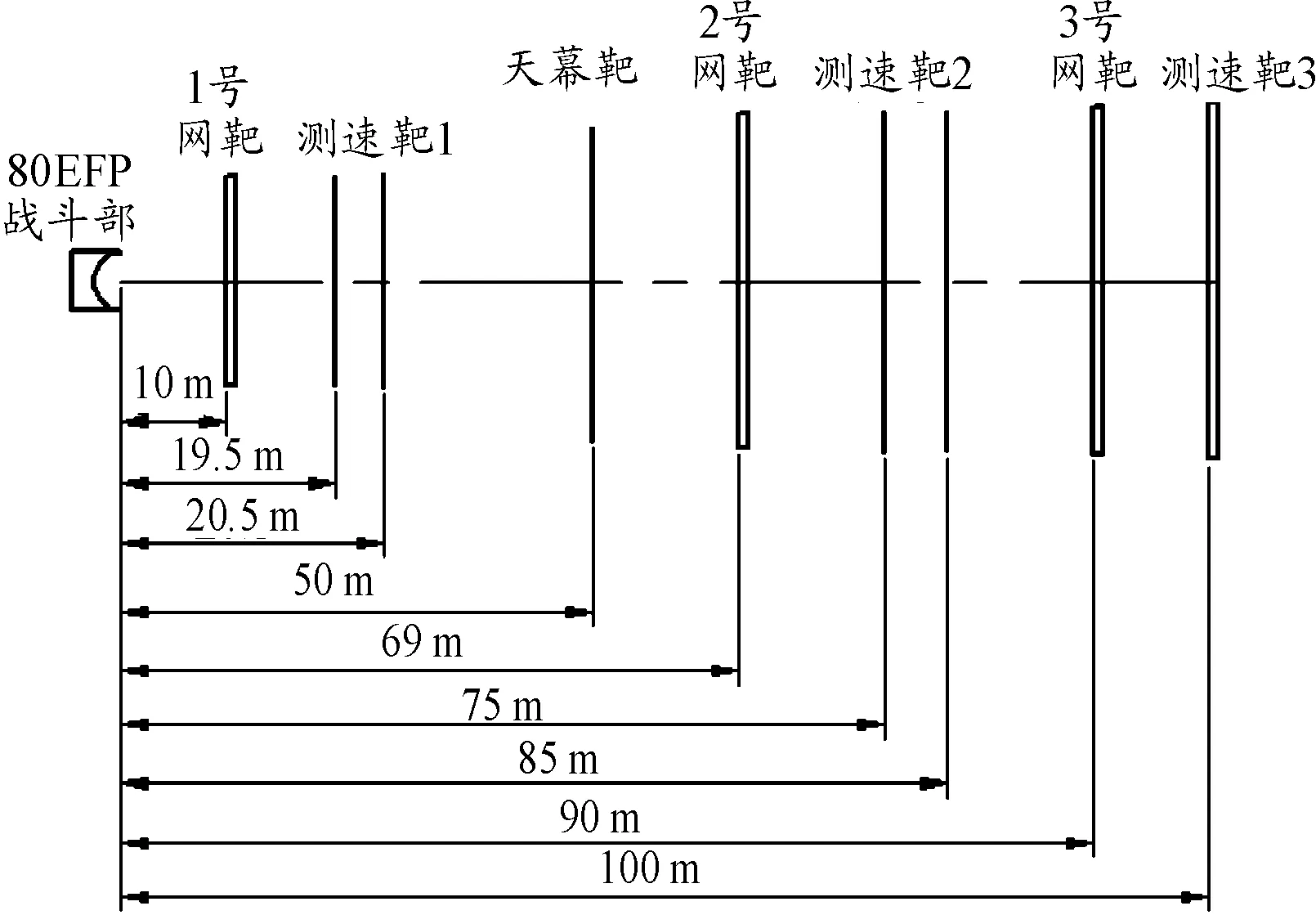
圖7 試驗(yàn)布置示意圖

3 試驗(yàn)結(jié)果和分析

3.1 試驗(yàn)結(jié)果及分析

穿靶形態(tài)與侵徹靶板情況如圖8、圖9所示。試驗(yàn)結(jié)果如表4所示。

第2發(fā)EFP穿透100 m處10 mm厚的裝甲鋼，入孔和出孔尺寸約為45 mm×43 mm，孔形近似圓形，靶板呈現(xiàn)沖塞破壞。說(shuō)明當(dāng)EFP著靶攻角較小時(shí)，其威力較大，表現(xiàn)為穿孔近似圓形，且發(fā)生沖塞破壞。

EFP戰(zhàn)斗部加工所形成的不對(duì)稱性以及起爆時(shí)的位置偏差、地面反射波作用、橫風(fēng)的影響都會(huì)對(duì)EFP飛行造成起始擾動(dòng)。試驗(yàn)中由于風(fēng)的影響，第3發(fā)EFP未著威力靶，也未測(cè)到在 2、3號(hào)網(wǎng)靶的穿靶形狀。依據(jù)經(jīng)驗(yàn)和第1、2發(fā)EFP的侵徹威力來(lái)看，所設(shè)計(jì)的EFP完全可穿透100 m處10 mm厚裝甲鋼。

根據(jù)EFP形成機(jī)理和所掌握的EFP的X光照片反映的形態(tài)[8]，EFP為頭部密實(shí)，帶有一定的尾翼張角的飛行體。由于無(wú)旋轉(zhuǎn)性，若要達(dá)到飛行穩(wěn)定必須如尾翼式彈丸一樣，應(yīng)當(dāng)具有相當(dāng)?shù)姆€(wěn)定儲(chǔ)備量。這種質(zhì)心在前、壓心在后，在一定的攻角下迎風(fēng)阻力繞質(zhì)心所形成的力矩將是攻角變小的穩(wěn)定力矩。在穩(wěn)定力矩作用下，尾翼式彈丸攻角的變化呈簡(jiǎn)諧振動(dòng)，考慮阻尼力矩作用時(shí)將使起始擾動(dòng)和穩(wěn)定力矩的擺動(dòng)運(yùn)動(dòng)很快衰減。

試驗(yàn)所測(cè)得EFP的網(wǎng)靶穿孔形態(tài)和靶板穿孔形態(tài)均良好，表明EFP是在穩(wěn)定力矩作用下克服起始擾動(dòng)作周期擺動(dòng)運(yùn)動(dòng)。

3.2 EFP飛行的速度與速度降

試驗(yàn)測(cè)得EFP飛行速度如表5所示。由表5可知，所設(shè)計(jì)的EFP 20 m處平均速度為1 732 m/s，平均速度降為7.4 m·s-1·m-1，按照EFP速度衰減的趨勢(shì)估計(jì)，初速約為2 000 m/s，與數(shù)值模擬結(jié)果接近。文獻(xiàn)[2]采用高能炸藥、優(yōu)質(zhì)罩材料等設(shè)計(jì)的EFP，初速可達(dá)2 000～3 000 m/s時(shí)，其速度降約為4 m·s-1·m-1。根據(jù)EFP速度保持的特性：初速越高、氣動(dòng)外形越好時(shí)，其速度降越小即保持速度能力越強(qiáng)。相對(duì)而言,本試驗(yàn)測(cè)得EFP的速度降還是比較令人滿意的。

圖8 第1發(fā)彈穿靶形態(tài)與侵徹威力

表4 試驗(yàn)結(jié)果

表5 EFP飛行的速度與速度降

4 結(jié)論

1) 數(shù)值模擬的EFP速度為2 100 m/s，形狀為短桿狀，這種形狀有利于EFP的遠(yuǎn)距離飛行、侵徹威力高。

2) 試驗(yàn)設(shè)計(jì)的EFP翻轉(zhuǎn)穩(wěn)定性良好，可穿透100 m 處10 mm厚裝甲鋼，入孔和出孔尺寸約為45 mm×43 mm，孔形近似圓形，是遠(yuǎn)距離攻擊硬目標(biāo)的理想戰(zhàn)斗部選擇。

3) EFP在20 m、50 m、80 m的平均速度為1 732 m/s、1 530 m/s、1 291 m/s，平均速度降約為7.4 m·s-1·m-1，按照EFP速度衰減的趨勢(shì)估計(jì)，初速約為2 000 m/s，與數(shù)值模擬結(jié)果接近。