基于SPSO優化Multiple Kernel-TWSVM的滾動軸承故障診斷*

徐冠基， 曾 柯， 柏 林

(重慶大學機械傳動國家重點實驗室 重慶, 400044)

引 言

滾動軸承是機械設備的重要零部件，其運行狀態關系著設備的正常運轉，國內外很多學者對滾動軸承的狀態監測做了大量的研究，并且隨著近年來人工智能領域的迅猛發展，滾動軸承的故障診斷技術得到了長足的發展。信號獲取的方法大多是采用加速度傳感器測量振動信號，特征提取是狀態辨識的大數據基礎，常用的振動信號特征提取方法包括時域分析，頻域分析以及時頻域分析。其中：時域分析包括峰值，峭度，均方根值和方差等；頻域分析包括快速傅里葉變換和離散傅里葉變換等；時頻分析法包括小波變換，短時傅里葉變換，希爾伯特變換和Winger分布等。上述特征提取方法是建立在振動信號是線性和平穩信號的基礎之上，而滾動軸承在高速運轉過程中滾動體與內外圈的接觸是非線性的，并且其載荷的分布以及接觸剛度的變化也是非線性的，因此滾動軸承在產生故障時會使其運轉周期消失并產生非線性振動[1]。傳統的線性、平穩特征提取技術，容易丟失重要的非線性狀態信息，不能很好地從復雜非線性信號中提取真實反映其非線性振動本質的有效狀態特征[1]。分形維數和熵特征利用相空間重構技術將滾動軸承振動信號映射到高維空間中以復原原始信號中的混沌特征[2]，分形維數是描述事物分形特性的一種有效方式，同時也是將事物分形特征進行量化的度量參數[3]，熵特征是用來反映系統的混亂程度和復雜性，熵累計得越多表示系統混亂程度越高，反之越低[4]，而系統的混亂程度和復雜性又與其故障狀態有著密切的關聯性。可見，利用分形維數和熵特征來對滾動軸承故障信號進行非線性特征提取能更加有效地辨識軸承的故障狀態。

狀態辨識的實質是機器學習與模式識別，近年來人工智能的快速發展促進了故障診斷技術的進一步提高，常用的模式識別方法有支持向量機和BP神經網絡等，SVM是一個二分類算法，對均衡或近似均衡分布的樣本，分類效果顯著[5]，如果遇到存在多種狀態類別的多分類問題，SVM只能通過二叉樹或者偏二叉樹等方法來細化分類，這樣做可能會導致訓練樣本不均衡問題，而SVM在處理該類問題時往往不盡人意[6]。Jayadev等[7]提出了TWSVM，TWSVM算法專門處理樣本非均衡問題，其核心思想是構造兩個非平行的超平面，使正類樣本靠近正類超平面而負類樣本盡可能地遠離，使負類樣本靠近負類超平面而正類樣本盡可能遠離。TWSVM其訓練速度較快，有著能較好求解異或問題和分類性能優越等明顯的優勢[8]，由于使用非平行的分類超平面，TWSVM在解決兩類樣本成交叉分布的分類問題時，具有更強的泛化能力[9]。TWSVM的主要原理在于是利用核函數來把高維向量空間中的內積計算轉換為原低維空間中某個函數的函數值代替，以解決訓練樣本線性不可分問題。其核函數的選擇與優化對其分類性能的提高起著至關重要的作用。不同種類的核函數也具有不同的特性，比如高斯核函數是局部核函數，多項式核函數是全局核函數，基于局部核函數和全局核函數的雙核函數[10]，基于高斯核和多項式核的雙核函數[11]等。但這些核函數改進融合大多用于提高傳統SVM模型分類性能中，尚未見對TWSVM核參數進行優化選擇的報道。因此，為解決其核函數性能單調的缺點，提出了將加權的高斯核和多項式核雙核函數引入到TWSVM分類模型，以提高TWSVM的分類性能和泛化能力，并采用簡化粒子群優化(simple particle swarm optimization,簡稱SPSO)[12]算法對核函數權值，分類模型參數和核參數尋優。實驗結果表明，基于分形維數和熵特征的非線性特征提取方法能夠有效地提取滾動軸承的故障特征，并且雙核TWSVM分類精度和泛化性能要高于單核TWSVM，另外在同等條件下對比BP神經網絡的分類精度，單核TWSVM和雙核TWSVM模型分類性能要優于BP神經網絡。

1 非線性特征提取

目前對于時間序列非線性特征的分析一般采用相空間重構法，時間序列相空間重構的原理是通過延時時間和嵌入維數把時間序列映射到更高維的空間中以便提取出原混沌時間序列中所含的非線性特征信息。

實現時間序列相空間重構的一種合適的方法是G-P算法[13]。

1) 選取合適的延遲時間τ和嵌入維數m對時間序列X={x1,x2,…,xN} 進行相空間重構，得到重構的相空間如式(1)所示

(1)

其中：Nm=N-(m-1)τ。

2) 計算累積分布函數

(2)

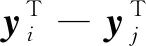
決定重構相空間的兩個重要參數是延遲時間τ和嵌入維數m，Takens[14]認為延遲時間τ和嵌入維數m的選取是相互獨立的過程。一般延遲時間(采用自相關函數法或者互信息法[15]，嵌入維數m可選用CAO法[16]，G-P方法[17]。

本研究擬采用關聯維數，盒維數，近似熵，樣本熵，模糊熵和Kolmogorov熵來提取時間序列非線性特征。關聯維數描述的是混沌時間序列具有某種確定規律及程度，經相空間重構后的時間序列相互關聯的點對個數越多，就表明系統運動的規律性就越強[2]。對于復雜機械設備的狀態變化，盒維數可以用來定量地描述分形邊界的統計自相似特性[18]。近似熵是用一個非負數來表示某時間序列的復雜性,越復雜的時間序列對應的近似熵越大[19]。模糊熵是衡量時間序列在維數變化時產生新模式的概率的大小，序列產生新模式的概率越大，則序列的復雜度越大，熵值越大[20]。樣本熵分析方法只需要較短數據就可得出穩健的估計值，是一種具有較好的抗噪和抗干擾能力的非線性分析方法[21]。Kolmogorov熵是非線性特性的度量特征量之一[22]，描述非線性系統產生信息量多少和快慢程度的物理量[23]。

2 基于SPSO的雙核TWSVM原理

TWSVM比較于傳統的SVM所建立的一個超平面，TWSVM構建了兩個不平行的超平面，并使正類樣本靠近正類超平面而負類樣本盡可能地遠離，而負類樣本靠近負類超平面而正類樣本盡可能遠離。非線性TWSVM的算法原理可參考文獻[5, 8]。另外，核函數的選擇對TWSVM的分類性能具有重要的作用，不同的核函數具有不同的分類特性，如上所述高斯核函數屬于局部核函數，多項式核函數屬于全局核函數。如何結合各個核函數的優點，并對其進行優化對提高TWSVM的分類性能具有重要的作用。全局核函數泛化能力強而分類能力較弱，局部核函數分類能力強而泛化能力弱，因此可以看出核函數的泛化能力與分類能力是相互制約的，這就需要找到一個平衡點讓雙核函數既具備較強的分類能力也要具備較強的泛化能力。因此將加權的高斯核和多項式核雙核函數其互補性強，應用到TWSVM分類模型中以解決其核函數性能單調的缺點，以此提高TWSVM的分類性能和泛化能力。

多項式核函數和高斯核函數是比較常見的兩種核函數。

高斯核函數

(3)

多項式核函數

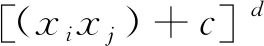
(4)

加權的高斯核和多項式核雙核函數如下

Kmix=mKpoly+(1-m)KRBF

(5)

其中：Kpoly為多項式核;KRBF為高斯核;m為調節核函數所占權值大小的參數。

假設矩陣A,B分別表示兩類樣本集，A∈Rm1×n,B∈Rm2×n，m1,m2分別表示樣本數量，n表示維度。將雙核函數Kmix帶入TWSVM中，可以得到雙核函數的TWSVM分類優化問題，如下

超平面1

s.t. 0≤α≤c1

(6)

其中：α=(α1,α2,...,αm2)T;G=[Kmix(B,CT)e2];H=[Kmix(A,CT)e1];CT=[ΑT,ΒT];z1=[u(1),b(1)]T=-(HTH)-1GTα;e1,e2為單位向量;c1為懲罰因子。

超平面2

s.t. 0≤γ≤c2

(7)

其中:γ=(γ1,γ2,…,γm1)T;P=[Kmix(A,CT)e1];Q=[Kmix(B,CT)e2];z2=[u(2),b(2)]T=(QTQ)-1·PTγ；c2為懲罰因子。

最終判別公式為

(8)

其中：Label為類別變量；class為具體類別。

從式(3)～(8)可看出，雙核TWSVM要優化的參數有懲罰因子c1和c2，高斯核參數σ，多項式核參數d,c以及雙核函數權值m。這些參數的選取對雙核函數TWSVM的學習能力及泛化能力有很大的影響，只有選擇出更優化的參數才能保證該方法的可靠性和穩定性，因此擬采用SPSO[12]的方法來確定最優參數，由粒子位置來控制粒子的更新，解決了算法后期收斂慢的問題。

SPSO算法首先是設定粒子數并對種群進行初始化，然后在每次迭代的過程中通過適應值函數來更新粒子的個體極值和全局極值，然后根據本次迭代后的個體極值和全局極值更新種群中所有粒子的位置。其位置更新方程為

(9)

其中：b1和b2為常數項，一般取值為2；r1和r2為[0,1]的隨機數；Pid為個體極值；Pgd為全局極值；xid為粒子位置；ω為慣性權重。

式(1)右邊第1項代表前一代粒子對后一代粒子的影響，第2項表示個體極值對粒子自身的反饋，第3項表示整個粒子種群的信息共享。SPSO只有位置更新方程而沒有速度參數項,其簡化和優化了粒子群計算規模。

3 實 驗

為了研究筆者提出的非線性特征提取方法和SPSO優化的雙核TWSVM對滾動軸承狀態類別的辨識性能，本研究選取由凱斯西儲大學提供的不同狀態類別的滾動軸承振動信號作為研究對象，實驗臺如圖1所示，包含了一個1.5 kW的電機，扭矩傳感器，譯碼器以及一個示功器。選擇驅動端軸承座上采集的加速度信號作為原始數據集，其采樣頻率為12 kHz，選擇的實驗軸承為SKF的深溝球軸承，采用電火花加工以模擬軸承故障類型和故障程度。

圖1 滾動軸承模擬故障振動實驗臺Fig.1 Test board of fault simulation of rolling bearings

數據集共包含4種狀態類別，分別為內圈故障，外圈故障，滾動體故障和正常狀態，每種故障類別包含有3種故障尺寸，分別為0.017 78，0.035 56，0.053 34 cm，再加上正常狀態，共計10種狀態類別，分別為正常，內圈故障為0.017 78，外圈故障為0.017 78，滾動體故障為0.017 78，內圈故障為0.035 56，外圈故障為0.035 56，滾動體故障為0.035 56，內圈故障為0.053 34，外圈故障為0.053 34，滾動體故障為0.053 34 cm。

在數據樣本的10種標簽類別中，每類標簽選取50個信號樣本，每個樣本信號截取2 048個點，一共構成500個信號樣本。對500個信號樣本提取非線性特征，即每個樣本分別提取關聯維數，盒維數，近似熵，樣本熵，模糊熵和Kolmogorov熵。由此組成維數為500×6的特征矩陣，所列特征值都經歸一化處理，去除量綱影響，其中6種故障類型部分特征向量參數如表1所示。

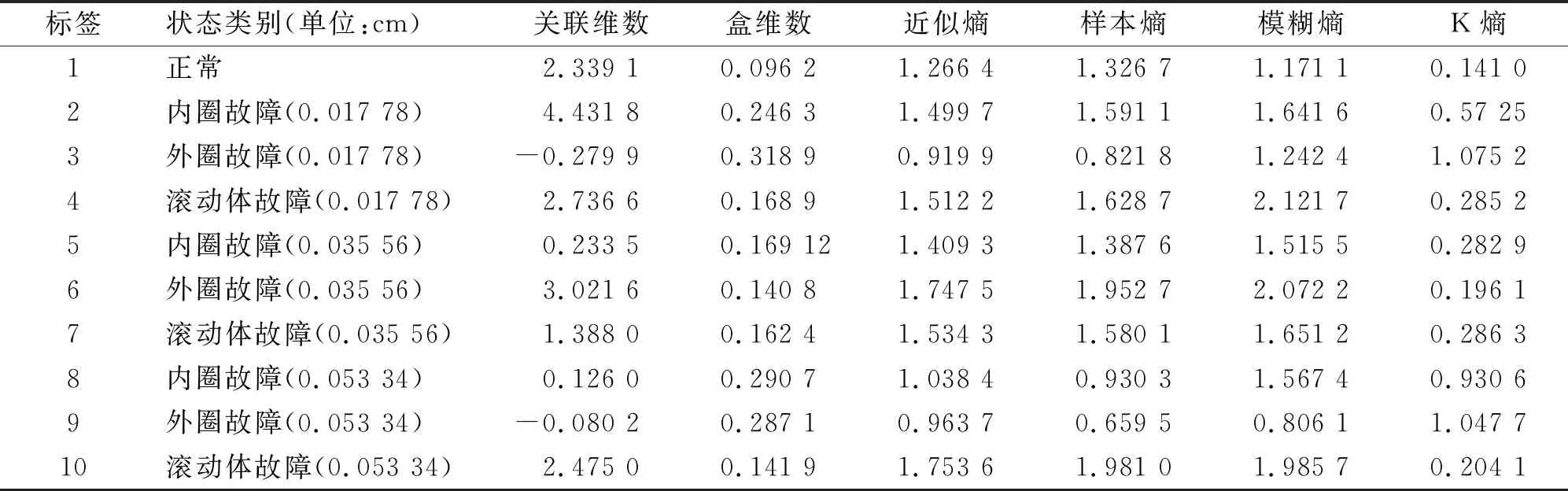
表1 非線性特征值表

從表1中可以看出，本研究所選取的6個特征對故障類別有很強的辨識能力，即參考某一特征下不同的狀態類型所對應的特征值大小不同，這是區別軸承狀態類別的一個基礎指標，也即特征值不同對應的狀態不同，當參考某一個特征下不同狀態的特征值會有相同，但是這只是在一個特征下(也即1維空間下)的樣本聚類特征，當特征越多進而特征向量的維度越高，在高維空間中不同狀態類別的數據樣本之間的區分度將會更好，重疊現象將會減少甚至消失。

另外,圖2中的(a)～(f)分別為關聯維數、盒維數、近似熵、樣本熵、模糊熵和Kolmogorov熵的特征值圖，橫坐標表示樣本數，即總共500個樣本，縱坐標表示特征值。從圖2中可以看出，不同狀態類別特征值的相互區分度較好，與表1所反映的情況基本一致，也出現了某些特征值圖在某些狀態類別下的特征值出現了重疊，正如前文所述那只是在1個特征也即1維空間下的樣本聚類特性。文中共選取了6個特征，這6個特征向量所組成的6維空間中，每個狀態類別樣本可以聚集在不同的空間區域，這將有利于雙核TWSVM建立分類超平面。

為了能夠直觀地觀察不同故障類別的樣本在空間中的聚集狀態，下面將畫出不同類別樣本的聚類圖，但是由于6維空間的點不能在人們所熟悉的笛卡爾坐標系中表示，笛卡爾坐標系最多只能表示三維空間的點。因此為了簡化該問題須在這6個特征中選擇每3個特征為一組，共4個組分別如圖3(a)～(d)所示，以研究特征的聚類程度。從圖3中可以看出，10種狀態類型的3維樣本點在空間中表現出分類聚集特點，每一個塊狀或云狀聚集點為一種故障類別，因此可以看出所選特征的聚類性很好。雖然觀察圖3可以發現不同狀態類別的樣本之間任有一些重疊，分析原因是因為所選取的特征值的維度只有3維，在將特征值維度擴展到6維之后，特征向量將被映射到更高維的空間中，將會具有更加明顯的特征聚類特性。

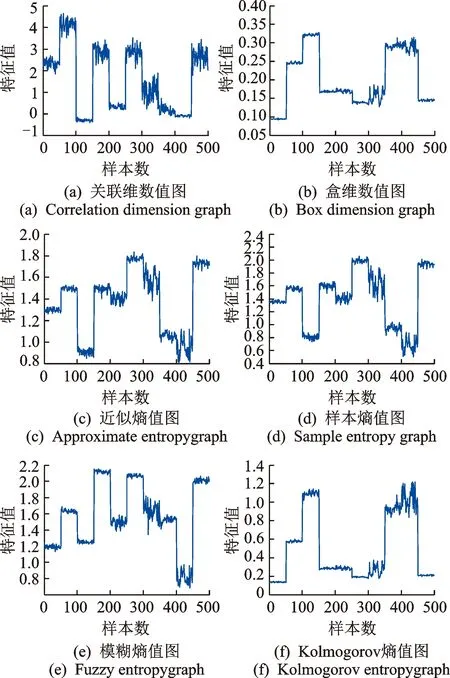
圖2 關聯維數、盒維數、近似熵、樣本熵、模糊熵和Kolmogorov熵的特征值圖Fig.2 Eigenvalues map about correlation dimension, Box dimension, approximate entropy, sample entropy, fuzzy entropy and Kolmogorov entropy

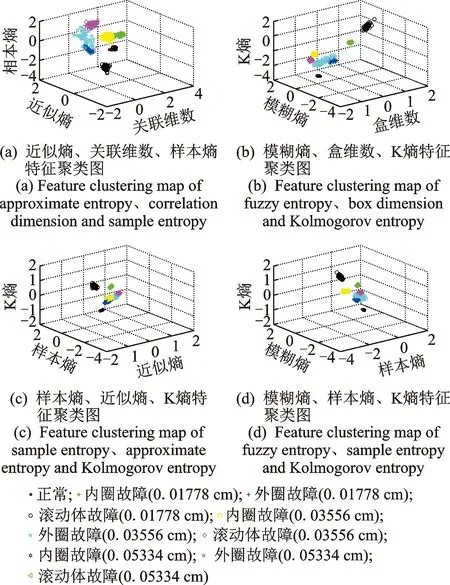
圖3 3個特征值維度下的特征聚類分析Fig.3 Clustering analysis of features based on three characteristic value

本實驗中對訓練樣本和測試樣本分配策略是在總共500個樣本中固定訓練樣本和測試樣本數，文中選定訓練樣本數為400個，測試樣本數為100個，并且訓練樣本和測試樣本互不交叉，然后再在總的400個訓練樣本中按25%，50%，75%和100%的比例抽取訓練樣本對分類模型進行訓練，用100個測試樣本進行分類預測得出當前比例下的分類準確率。

單核的TWSVM所用到的核函數是高斯核函數，高斯核函數是一種局部核函數，其分類能力強而泛化能力弱，為了兼顧TWSVM的泛化性能和分類能力，現將高斯核函數和多項式核函數通過加權的方式組成雙核函數引入到TWSVM中，在雙核TWSVM模型的訓練中采用的SPSO方法對參數進行優化。在第2節中提到了需要優化的參數有懲罰因子c1和c2，高斯核參數σ，多項式核參數d和c以及雙核函數權值m，上述參數均無量綱。由于SPSO算法的計算量會隨著優化參數的增加呈現近乎指數型增長，因此為了提高優化效率需減少待優化參數個數，多項式核函數中參數c和d的選擇[24]一般比較固定，取c=1,d=2.需要優化的參數只剩下c1和c2，σ和m，試驗表明只需設置種群大小為30，當迭代次數為30次時適應度函數就可達到最大值。

表2列出了在訓練樣本比例為50%的情況下SPSO對上述4個參數的優化情況。針對10種狀態類別需要采用偏二叉樹的方法來建立訓練模型,因為TWSVM與SVM一樣都是二分類模型，即一次只能進行兩種狀態類別的劃分，如果遇到多分類問題，就要采用二叉樹或者偏二叉樹的方法來實現，采用偏二叉樹對10種狀態類別進行分類就需要訓練9層分類模型，第1層區分第1類和第2345678910類，第2層區分第2類和第3456789類，以此類推，第9層區分第9類和第10類。m表示高斯核函數的權重，多項式核函數的權重自然為1～m。從表中可以看出，分類模型的不同層次中，高斯核和多項式核的權重有很大的差別，這就說明雙核能通過調整權重的大小來適應不同的訓練樣本的空間分布特性以平衡分類超平面的泛化性能和分類能力。

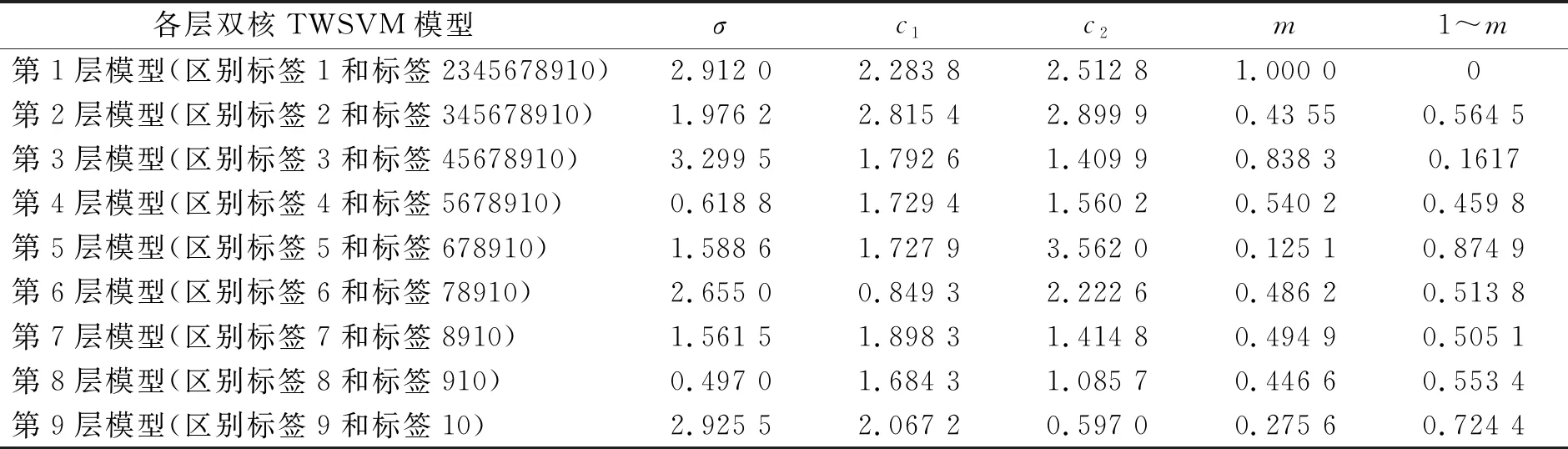
表2 訓練樣本比例為50%時各層雙核TWSVM模型參數取值情況

為了得到最終穩定的分類準確率，將每個訓練樣本比例下的訓練和預測重復進行10次，由于訓練樣本的抽取是隨機的，因此重復10次取平均能夠得到較為穩定的預測精度。

表3給出了單核TWSVM，雙核TWSVM和BP神經網絡在不同的訓練和測試樣本比例情況下的識別性能。從表中可以看出，3種分類模型的識別準確率不管是在小樣本和多樣本情況下都能達到90%以上，仔細分析主要是因為筆者提出的非線性特征提取方法所提取出的特征向量具有很高的聚類特性，也即類別辨識度高，這有助于建立精準的分類超平面。另外，對比TWSVM和BP神經網絡兩種分類方法，TWSVM整體上要高于BP神經網絡 ，這是TWSVM分類性能優越能夠有效提高故障辨識精度[8]，這也證明了TWSVM具有很強的泛化性能。在保證TWSVM泛化性能的基礎上并提高TWSVM的分類精度，根據表3可以看出，基于雙核的TWSVM相對于單核的TWSVM整體有一定提升，雙核TWSVM的分類準確率能夠達到100%左右，特別是在小樣本情況下，即訓練樣本比例只有25%時，雙核TWSVM相對于單核TWSVM分類準確率提高了8%左右。

表3 單核TWSVM、雙核TWSVM和BP神經網絡在不同訓練樣本比例下識別性能

4 結束語

筆者將非線性特征分析方法用來對10種狀態類型的滾動軸承振動信號進行特征提取。實驗結果表明，所提取的特征樣本具有很好的類別辨識度，這為雙核函數的TWSVM模型的訓練提供了準確的樣本依據。另外，由于TWSVM本身具有解決兩類樣本成交叉分布的分類問題時，具有更強的泛化能力以及分類準確性，實驗中也證實了TWSVM的預測精度整體上要優于BP神經網絡。但是TWSVM核函數的選擇對于分類模型的泛化能力和分類性能有較大影響，而泛化能力和分類性能又是相互制約的，為了尋找平衡點，本研究將加權的高斯核和多項式核組成雙核函數引入到TWSVM以提高其泛化能力和分類性能。從實驗結果可以看出，在不同的訓練樣本比例下特別是小樣本比例下，雙核TWSVM的預測精度都要高于單核TWSVM，這說明雙核函數能通過調整權重的大小來適應和平衡分類超平面的泛化性能和分類能力。因此筆者提出的非線性特征提取方法和雙核TWSVM分類模型對提高滾動軸承故障診斷準確率具有重要意義。