螺旋溝槽參數對縱-扭變幅桿振動分量的影響*

趙 波， 殷 森， 王曉博， 趙重陽

(河南理工大學機械與動力工程學院 焦作,454000)

引 言

隨著現代工業的飛速發展，脆難加工材料，特別是金屬基復合材料及納米復相陶瓷加工需求日益增加。超聲振動加工技術因其在硬脆材料加工中的突出優勢，得到廣泛的研究及應用[1]。單一的超聲振動模式已不能滿足日益復雜的加工要求，超聲加工系統的復合振動模式開始得到國內外學者的關注。復合振動模式主要有縱彎復合、扭彎復合[2]、縱扭復合[3]、雙彎曲復合[4]及徑扭復合[5]等。目前，實現縱-扭復合振動的方式大致可以分為兩種:a.通過換能器實現，如利用極化方向不同兩組壓電陶瓷組成的縱-扭復合振動換能器[6]、利用軸向磁致伸縮產生扭轉振動的換能器[7]和將壓電陶瓷進行傾斜布置的縱-扭復合換能器[8]；b.通過變幅桿實現，如對其結構進行特殊化設計，在變幅桿上添加“模態轉換器”，將縱向振動模式進行轉換與復合，如螺旋槽式變幅桿[9]、斜槽式變幅桿[10]及榫卯式變幅桿[11]。

對于螺旋溝槽式縱-扭復合變幅桿而言，其扭轉振動分量較高，縱-扭復合振動的輸出較為穩定。作為縱-扭復合振動的模態轉換器的螺旋溝槽結構，其結構參數的變化會對縱向振動分量及扭轉振動分量產生一定的影響，從而改變變幅桿輸出端的振動軌跡[8]。筆者利用理論推導、有限元分析與實驗驗證相結合的方法，探究了螺旋溝槽結構參數對變幅桿的縱向振動分量與扭轉振動分量的影響。通過對螺旋溝槽結構參數的合理選擇，可實現對扭縱分量比j的調整，從而對超聲橢圓振動軌跡進行精確控制。

1 縱-扭模態轉換與振動軌跡的理論分析1.1 螺旋溝槽的縱-扭模態轉換

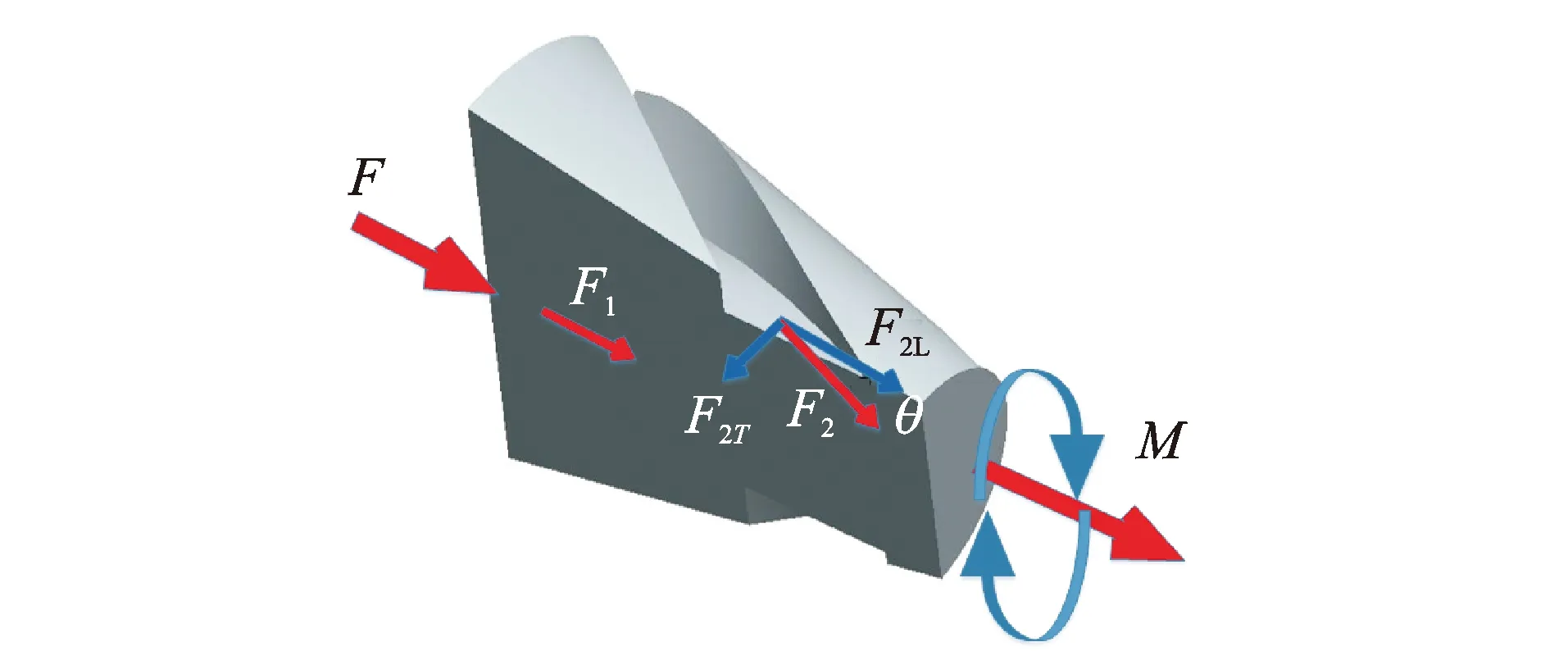
圖1 圓錐變幅桿上開設螺旋溝槽Fig．1 Helical slots are formed on the conical horn

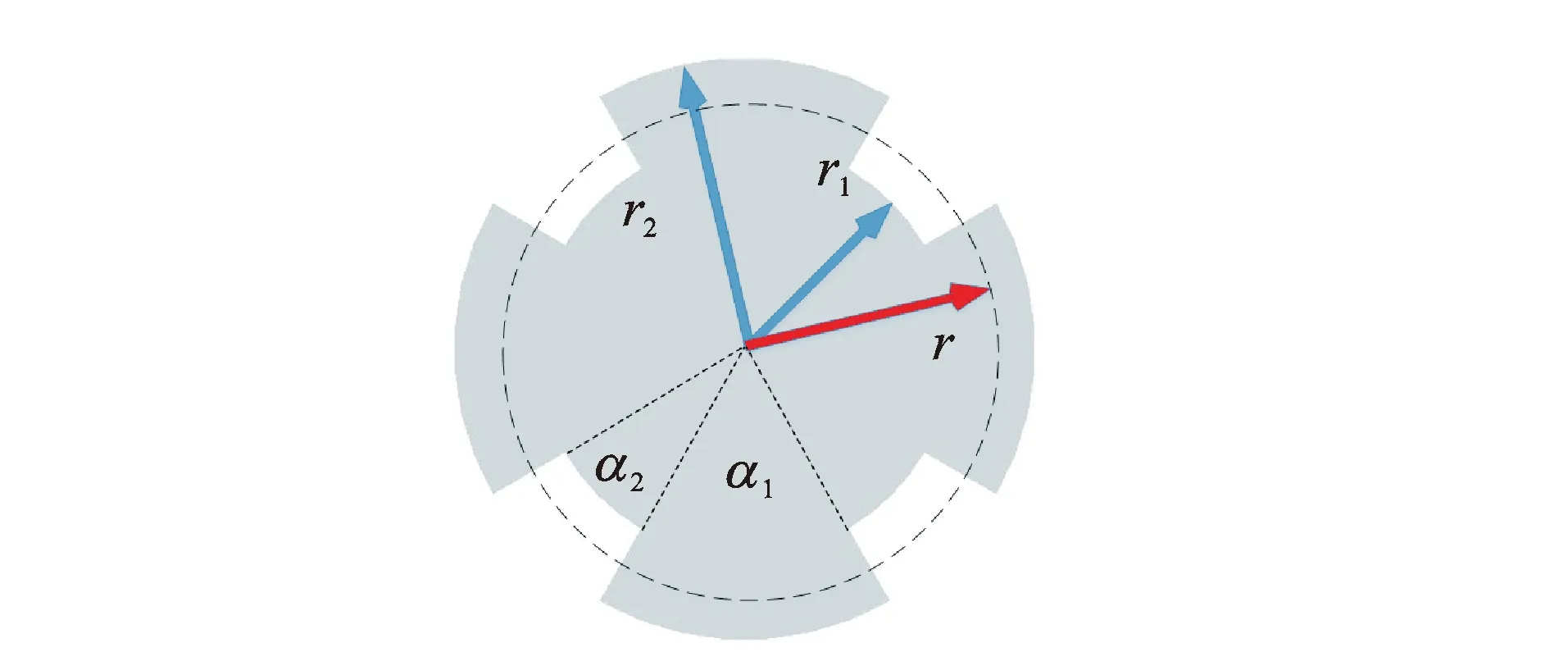
圖2 螺旋溝槽切口形狀Fig．2 Helical slots incision shape

在一圓錐形變幅桿側面上開設均布螺旋溝槽，如圖1所示。圖中：F為縱波產生的縱向慣性力；F1和F2分別為F沿螺旋溝槽分解的力；F2L為縱向作用力分量；F2T為及剪切作用力分量；M為剪切作用力產生的扭矩。結合變幅桿強度要求及機械加工難度，將溝槽設計成類梯形狀，溝槽所包絡為一實心圓柱，溝槽的長度為變幅桿母線長度如圖2所示，圖中：r為變幅桿任意橫截面的截面半徑；r1為實心部分半徑，即變幅桿小端半徑；r2為變幅桿大端端面半徑；α1為相鄰溝槽間未切除部分對應的圓心角；α2為溝槽部分對應的圓心角。

縱波在空氣介質中傳播時，會發生較大的能量損耗，故在縱波傾斜入射螺旋溝槽時，可只計算反射縱波和反射橫波的影響，而忽略縱波二次折射所產生的影響[12-13]。縱波產生的縱向慣性力F將分解為F1和F2：在溝槽所包絡實心圓柱中的力F1將繼續沿縱向傳遞；在螺旋溝槽結構部分截面上的力F2沿溝槽旋轉方向與F成θ夾角。F2將分解成兩部分：縱向作用力分量F2L及剪切作用力分量F2T，其中縱向作用力分量沿著變幅桿軸線方向；關于剪切作用力分量，在截面上任一點的剪切作用力分量垂直于半徑的方向，由剪切作用力分量產生的總力矩是所有剪切作用力在整個截面上扭矩的積分。

由圖1可知，這兩個力分量大小可由下式給出

F2L=F2cosθ

(1)

F2T=F2sinθ

(2)

其中：θ為螺旋溝槽的螺旋角。

根據縱向振動及扭轉振動理論，縱向力將驅使變幅桿產生縱向振動，而剪切作用力將驅使變幅桿產生扭轉振動。剪切作用力產生的扭矩M可以表示為

(3)

由圖2可知，變幅桿任意橫截面面積s為

(4)

變幅桿任意橫截面半徑為r處的微分元面積ds為

(5)

變幅桿任意橫截面上的剪切作用力f為

(6)

將式(24),(25)代入式(26)可以得到

(7)

其中：r2為變幅桿大端端面半徑。

化簡并求得

(8)

故由于螺旋溝槽的存在， 可使單向模態的縱向振動激勵實現超聲縱-扭復合振動的輸出。由此式可知:縱向慣性力F由縱振換能器提供，為定值；r1,r2為復合變幅桿尺寸，其也為確定值。

由圖1可知

α1+α2=360/n

(9)

其中:n為螺旋溝槽數目。

α1,α2與螺旋溝槽數目n相關，而α2對應的的弦長與螺旋溝槽的槽寬d相關，故扭矩M與螺旋溝槽的數目n，溝槽角度θ及溝槽槽寬d等變量相關，即扭轉分量大小與此3個因素的取值有關。

1.2 輸出端上質點軌跡分析

前文中分析，螺旋溝槽使得縱振換能器所激勵的部分縱振振動轉換為扭振振動，而另一部分則直接傳遞到變幅桿輸出端。由于這兩種振動在相同介質中的傳遞路徑及傳遞速度均有不同，故變幅桿輸出端上的質點的運動軌跡是在兩個頻率相同但相位不同的縱、扭振振動的共同作用[8]。

在變幅桿輸出端面上取不在軸線上的任意質點P，設un代表質點扭轉振動的線位移，uz代表質點沿變幅桿軸線方向的縱向振動位移，則質點P的振動軌跡方程可以表示為

(10)

其中：ω為換能器激勵頻率；Uz，Un分別為質點P的縱向振動與扭轉振動位移振幅；φ為縱向振動與扭轉振動的相位差。

對式(10)進行分解，可得

un/Un=sinωtcosφ+cosωtsinφ

(11)

由式(10)可得

uz/UZ=sinωt

(12)

將式(11)代入式(12)中，可得

(13)

整理可得

(14)

從式(14)中可知，當質點P的縱向振動與扭轉振動位移的相位差達為φ時，其運動軌跡為一橢圓，且該橢圓軌跡的形狀及運動方向與φ的取值有關。當相位差φ為不同的數值時，可以得到如圖3所示的各種運動軌跡。

圖3 質點在不同位移相位差下的運動軌跡Fig．3 The trajectory of the particle under different displacement phase difference

螺旋溝槽結構作為扭轉振動的模態轉換器，其轉換的縱向振動及扭轉振動的分量是相互獨立的，因此，質點P不同的縱振振幅與扭轉振幅的比值可使其刻畫不同的運動軌跡，如圖4所示。

圖4 橢圓運動軌跡與縱扭兩振幅的關系Fig．4 The relation between elliptical motion trajectory and longitudinal and torsional amplitude

由式(8)，(9)可知，使變幅桿發生扭轉振動的扭矩M大小與螺旋幾何溝槽的參數相關，因此，合理選擇螺旋溝槽參數，可改變復合振動中縱向振動分量與扭轉振動分量，從而實現對質點運動軌跡的控制。為縱-扭復合超聲電機的開發利用提供了參考，對推廣縱-扭復合超聲振動加工具有重要意義。

2 螺旋溝槽變幅桿的有限元分析

為了同時獲得較大的變幅桿放大系數和形狀因素，設計圓錐過渡式階梯型復合變幅桿[14]。選用價格低廉，易加工且疲勞強度較高的45#鋼，設計諧振頻率為35 kHz的變幅桿，其結構尺寸如圖5所示。在其圓錐段開設4條均布的溝槽，形狀如圖1,2所示，螺旋角度為θ=45°，槽寬為d=8 mm、槽深為h=7.5 mm(以圓錐段大端為基準)。

圖5 圓錐過渡式階梯型復合變幅桿結構尺寸Fig．5 Composite horn structure dimension drawing

利用PRO/E軟件對螺旋溝槽變幅桿進行三維建模，并導入有限元分析軟件ANSYS中，進行模態分析，網格劃分時選取20個節點的solid95單元，采用自由網格，設精度等級為4，模態分析提取方法為Subspace，模態拓展階數為10，模態搜索設置范圍為30～40 kHz。針對切除螺旋溝槽后的變幅桿頻率少量偏移，通過調整變幅桿的結構尺寸，將諧振頻率修正至35 kHz，圖6為上述溝槽參數下變幅桿的模態分析結果。

螺旋溝槽式變幅桿的位移等值線如圖6(a)所示，變幅桿振動較為均勻。通過模態分析的振型向量圖6(b)可知，螺旋溝槽結構對變幅桿的振型進行了轉換，與理論推導結果相吻合。

2.1 單個螺旋溝槽參數的影響

分別改變螺旋溝槽數目n、螺旋角度θ、槽寬d等參數，采用相同的ANSYS軟件設置參數，逐一進行模態分析，提取縱-扭復合振動模態。螺旋溝槽結構參數的變化對變幅桿放大倍數m的影響如圖7所示。

由圖7(a)(b)可知，變幅桿放大倍數m隨螺旋溝槽數目n、螺旋角度θ、槽寬d的變化產生輕微的波動，且其波動范圍非常小。可認為螺旋溝槽結構參數的變化對變幅桿放大倍數m基本無影響。

圖6 螺旋溝槽式變幅桿的模態分析結果Fig．6 Modal analysis results of horn with helical slots

圖7 螺旋溝槽參數對變幅桿放大倍數m的影響Fig．7 Effect of helical slots parameters on magnification m

模態分析中的位移不是絕對位移，但可利用相對位移來代替絕對位移，進行縱向振動分量與扭轉振動分量的對比。定義螺旋溝槽變幅桿輸出端面不在軸線上某一質點P的扭轉振動位移Un與縱向振動位移Uz之比為扭縱分量比j，即

j=Un/Uz

(15)

螺旋溝槽結構參數的變化對扭縱分量比j的影響如圖8所示。

圖8 螺旋溝槽參數對扭縱分量比j的影響Fig．8 Effect of helical slots parameters on the torsional and longitudinal component ratio j

由圖8(a)可知，螺旋溝槽槽寬d的大小對扭縱分量比j的影響較小，變幅桿輸出端上的質點P的扭縱分量比j隨槽寬d的改變略有增加；在溝槽數目為2～5個時，P點的扭縱分量比j隨溝槽數目n的增加而顯著增加，即扭轉分量變大，當溝槽數目n繼續增大，扭縱分量比增加趨緩。由圖8(b)可知，質點P的扭縱分量比j隨螺旋角度θ的增大而增大，并在35°時達到峰值，之后(當θ>35°時)，扭縱分量比隨螺旋角度θ的增加逐步減小，直到θ=90°時j趨近于0。

綜上所述，螺旋溝槽數目n、螺旋角度θ、槽寬d等參數的變化對變幅桿的輸出“總量”無影響，只是改變了縱向振動分量與扭轉振動的分量的比值。

2.2 多個螺旋溝槽參數的影響

采用如表1所示的三因素三水平正交參數進行模態分析，分析多個螺旋溝槽參數對變幅桿輸出端某質點扭縱分量比的影響。通過極差R1的分析，影響縱扭分量的主次順序為螺旋溝槽數目n>螺旋角度θ>槽寬d。

表1 正交螺旋溝槽參數與扭縱分量比的三因素三水平極差分析

3 實驗分析

3.1 扭轉測評方法

模態分析中定義的材料是均勻的，而實際加工所用的材料的大都均勻性不好，存在或多或少的缺陷，由此導致實際結果與仿真結果的偏差。為驗證有限元分析的結果，現加工出螺旋角度為30,45和60°的螺旋溝槽變幅桿，每個角度分別開設2個和4個螺旋溝槽，溝槽的槽寬d=6 mm，槽深h=7.5 mm。

為精確測定質點P的扭振振幅，設計了一種扭轉振動測評方法。如圖9所示，對變幅桿進行加工，在小圓柱端面上沿其直徑切除一個半圓形臺，在變幅桿徑向方向上形成一個平面，如圖10所示，沿變幅桿徑向方向將小圓柱段半徑進行7等分，即劃分8個測定點。測定點編號及其對應的與變幅桿軸線的距離如表2所示。借助型號為VW9000高速攝影儀及高精度激光位移傳感器將激光束精確定位到每個測定點上，對每個測定點扭轉振幅Un的測定。測定點的劃分及扭轉計算原理如圖11所示，扭轉振動測評現場如圖12所示。

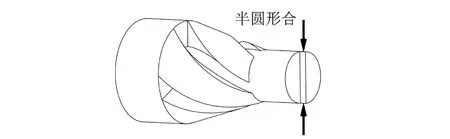
圖9 加工后的變幅桿結構示意圖Fig．9 The schematic diagram of the horn structure after processing

圖10 變幅桿上的測定面結構Fig．10 Measurement surface structure on the horn

Tab.2Thedistancebetweenthemeasurepointandhornaxis

測定點12345678距變幅桿軸線距離/mm01234567

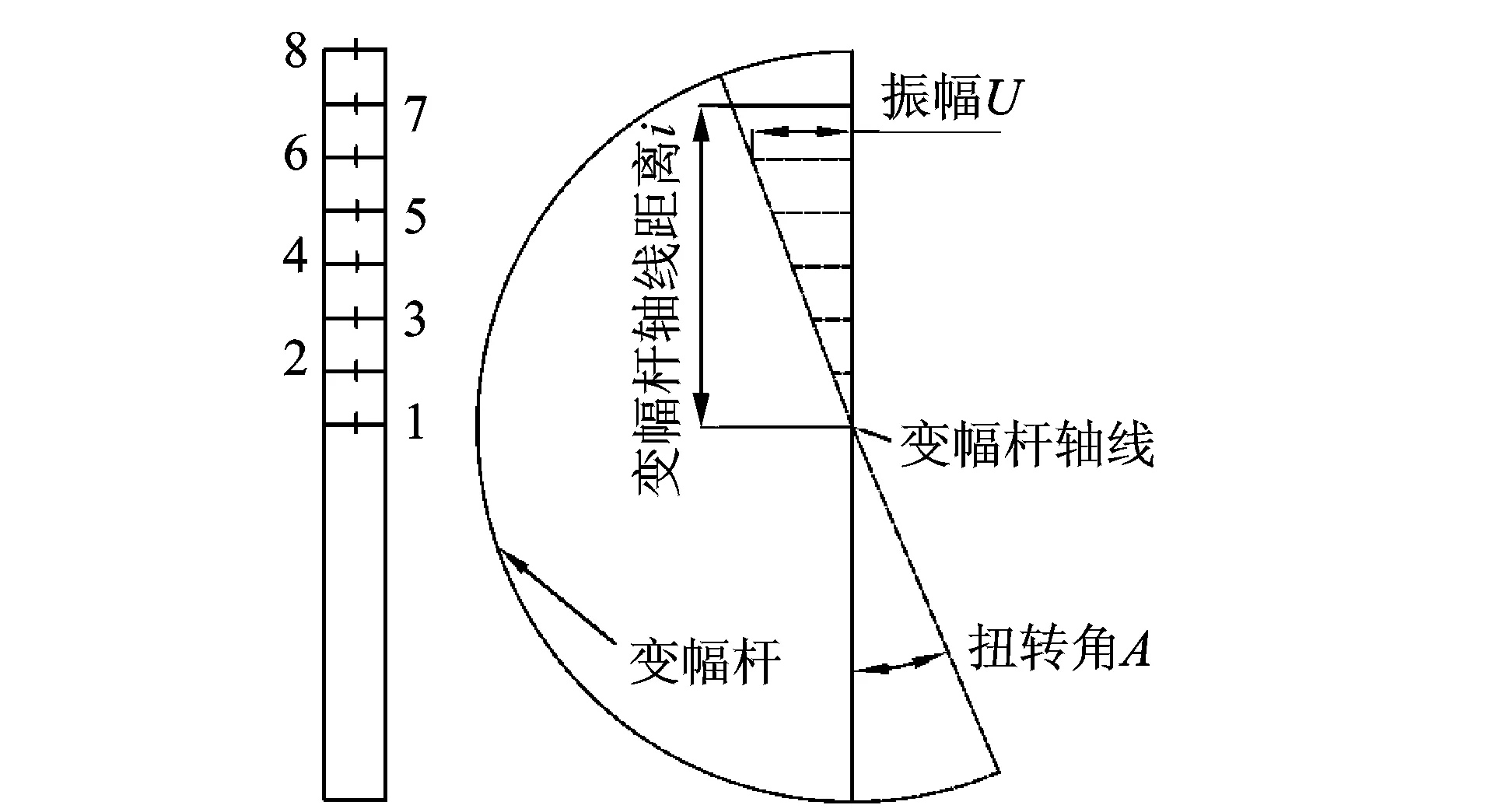
圖11 測定點的劃分及扭轉計算原理Fig．11 The division of measurement points and the principle of torsion amplitude calculation

圖12 扭轉振動測評現場Fig．12 Torsional vibration measurement site

以測定點與變幅桿軸線的距離i作為橫坐標，扭轉振幅Un為縱坐標，利用測定數據繪制扭轉振幅測定曲線，采用最小二乘法擬合出一條正比例函數y=1.35x，即建立該變幅桿的扭轉幅度函數曲線，如圖13所示。

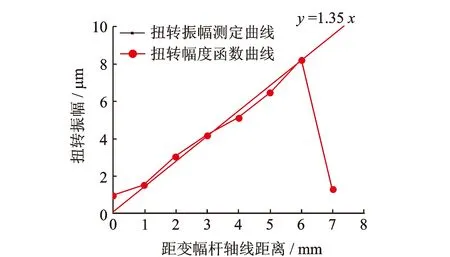
圖13 扭轉幅度函數曲線Fig．13 Torsion amplitude function curve

圖13中可看到，在8號測定點，扭轉振幅Un急劇下降，與扭轉幅度函數曲線有較大偏差。究其原因：8號測定點位于變幅桿半徑的邊緣處，變幅桿扭轉振動時，激光有段時間沒有集中在變幅桿上，傳感器接收不到反射引號，造成扭轉振幅Un測量的不準確。

變幅桿扭轉振動角度正切值e

e=tan∠A=Un/i

(16)

其中：A為變幅桿的扭轉振動角度。

扭轉幅度函數曲線的斜率k為變幅桿扭轉振動角A的正切值e，測量質點P到變幅桿軸線的距離i=6.4 mm。

質點P的扭轉振幅可近似通過擬合的曲線進行計算

Un=iPe=iPK=6.4×1.35=8.64 μ m

(17)

3.2 實驗與仿真結果的對比

縱向振動的輸出在變幅桿輸出端面是均勻的，故將激光束集中在端面上即可測量縱向振幅，其縱向振幅為Uz=11.8 μm。即質點P的扭縱分量比

j=Un/Uz=8.64/11.8=0.71

(18)

使用該方法對所加工的系列變幅桿相同位置的質點的扭縱分量比進行測定，實測結果與仿真結果的誤差很小，實測質點P的扭縱分量的變化趨勢與仿真結果的變化趨勢基本一致，如圖14所示。

圖14 縱扭分量的實測結果與仿真結果的對比Fig．14 Comparison of measured results of longitudinal and torsional components with simulation results

4 結束語

筆者理論推導了螺旋溝槽結構的縱-扭模態的轉換，分析了縱振振幅與扭轉振幅對變幅桿輸出端的橢圓振動軌跡的影響。基于有限元仿真探究了螺旋溝槽參數對變幅桿振動特性的影響，對部分結果設計實驗加以驗證，可以得到以下結論：a.螺旋溝槽數目n、螺旋角度θ、槽寬d的變化對變幅桿放大倍數m基本無影響;b.變幅桿輸出扭縱分量比j隨槽寬d的增加略有上升；隨螺旋溝槽數目n的增加而變大；隨螺旋角度θ的增加的先上升而后下降。影響縱扭分量的主次順序為螺旋溝槽數目n>螺旋角度θ>槽寬d。

在縱振式變幅桿上開設螺旋溝槽，成功輸出縱-扭復合振動。通過合理選擇螺旋溝槽幾何參數，實現對輸出端的扭縱分量比j的控制，從而得到超精密加工所需的橢圓振動模式。