超聲縱-扭復合鉆削系統的力負載影響研究*

常寶琪， 趙 波， 原路生， 李鵬濤， 趙重陽

(河南理工大學機械與動力工程學院 焦作，454000)

引 言

鈦合金(Ti6A14V)作為一種先進材料，具有強度大、抗蝕性好、耐磨損、耐熱性強及密度小等性能，被廣泛應用于現代航空航天工業[1-2]。同時，鈦合金屬于難加工材料，傳統鉆削加工難以實現高質高效的加工效果。超聲輔助鉆削加工作為一種先進的特種加工技術，在鈦合金和鎳合金等難加工金屬材料的鉆孔過程獲得良好的工藝效果，有效降低了孔表面粗糙度、孔出口毛刺高度和刀具磨損[3-5]。但是在超聲輔助鉆削鈦合金等難加工材料中，較大力負載的出現會使聲學系統的電流波動、頻率偏移，導致聲學系統不穩定甚至失諧。因此，研究力負載變化對聲學系統特性的影響機理和規律，對提高超聲輔助鉆削加工效果具有十分重要的意義。

關于負載對超聲振動系統特性的影響，已有學者進行了相關研究。伊曉春等[6]基于瞬態波傳播理論，研究了周期激勵下階梯形變幅桿重復撞擊加工工件的瞬態動力響應及特性變化。文獻[7]根據刀具的幾何參數變化，分析刀具負載對超聲銑削聲學系統穩定性的影響。針對力負載，劉折等[8]通過研究負載施加接觸方式為點、線、面時，負載對超聲加工聲學系統特性的影響。文獻[9]研究了超聲車削中車削力與切削速度﹑切削深度以及切削質量之間的關系。張云電等[10]通過分析不同珩磨方式下的珩磨壓力，得出系統承受不同珩磨力下諧振頻率的變化規律。紀華偉等[11]通過對超聲切割聲學系統理論模型的建立，得到超聲切割力與系統諧振頻率及阻抗之間的關系。也有學者利用有限元仿真和理論分析相結合的方式，揭示了刀具負載、換能器和變幅桿組成的振動系統的各種諧振狀態特性,研究了系統的諧振設計方法[12]。

綜上所述，對于鈦合金材料超聲鉆削聲學系統的研究略顯不足，不同力負載下，超聲鉆削系統的阻抗值、振幅和諧振頻率變化規律尚不明確，超聲鉆削系統在實際加工中不夠穩定。根據以上問題以及實際加工中出現的系統失諧、振幅衰減甚至停振等現象，基于四端網絡法對由換能器﹑復合變幅桿和負載三者組成的超聲鉆削聲學系統進行理論分析，獲得系統阻抗和放大系數隨負載的變化規律。基于有限元仿真研究了模擬力和周期鉆削力對聲學系統振動特性的影響，通過模擬試驗與鉆削加工試驗,研究了負載變化對超聲振動參數的影響規律。

1 超聲鉆削聲學系統整體理論模型

1.1 超聲復合變幅桿的等效四端網絡模型

筆者采用圓錐過渡型復合變幅桿，將復合變幅桿的每一段等效為一個機械四端網絡,然后將各傳輸矩陣連續相乘,得到一個整體四端網絡及其傳輸矩陣[13]。圖1為圓錐過渡復合變幅桿的結構簡圖。圖2為復合變幅桿的總體四端網絡圖。

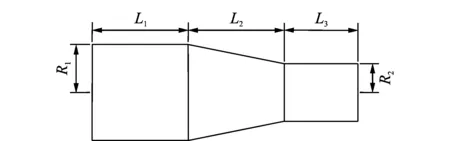
圖1 圓錐過渡復合變幅桿結構簡圖Fig.1 Conical transition composite horn structure diagram

圖2 復合變幅桿總體四端網絡圖Fig.2 Composite horn overall four-terminal network diagram

根據一維縱振桿波動方程、力和位移的邊界條件，得到各段變幅桿的傳輸方程[14]如下所示。

變幅桿大圓柱段傳輸方程

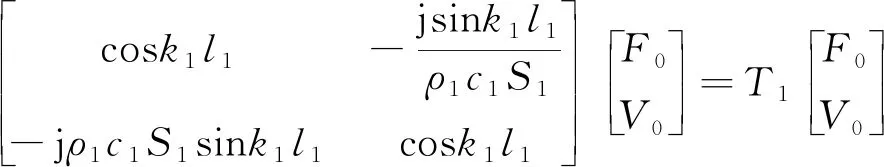
(1)

變幅桿圓錐段傳輸方程

(2)

變幅桿小圓柱段傳輸方程

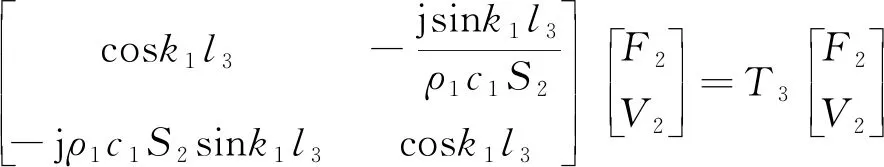
(3)

其中：T1，T2，T3分別為變幅桿各段傳輸方程中的傳輸矩陣；S1和S2分別為復合變幅桿大端和小端面積；c1為聲波在變幅桿中傳播速度；k1=ω/c1為圓波數；ρ1為復合變幅桿的密度。

聯立式(1)～(3)，可得復合變幅桿的總體傳輸方程為

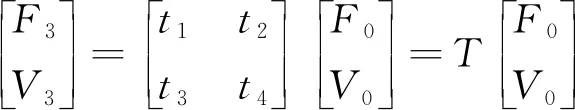
(4)

其中：T=T3T2T1。

1.2 壓電陶瓷的等效四端網絡模型

壓電陶瓷是一個電輸入到力輸出的元件，壓電陶瓷向兩端面輸出力，這兩個端面分別與前﹑后端蓋相連[15]。由于后端蓋是作為聲能的反射面，所有的負載以及工作端都在前端蓋方向，故在分析時只選擇前端蓋作為研究對象。

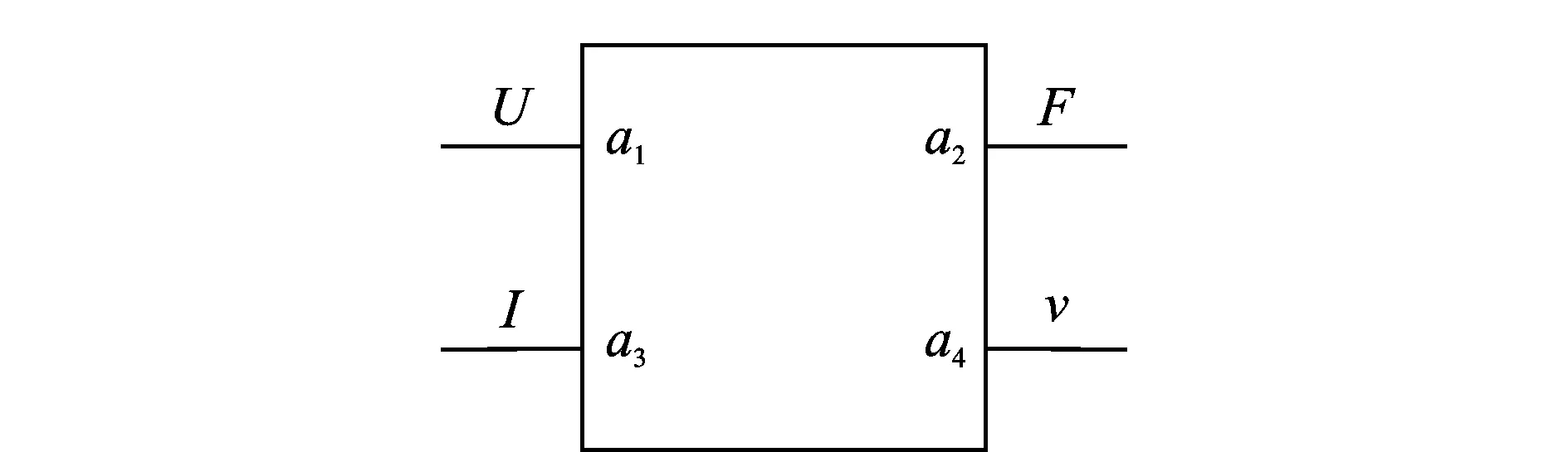
圖3 壓電陶瓷四端網絡示意圖Fig.3 Piezoelectric ceramic four-terminal network schematic

根據使用條件和特性，筆者選擇圓柱形壓電陶瓷。當壓電陶瓷滿足一維軸向縱振時，對于無損耗的壓電材料，結合牛頓第二定律、電荷守恒方程和邊界條件，求得壓電陶瓷傳輸方程[16]為

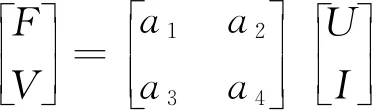
(5)

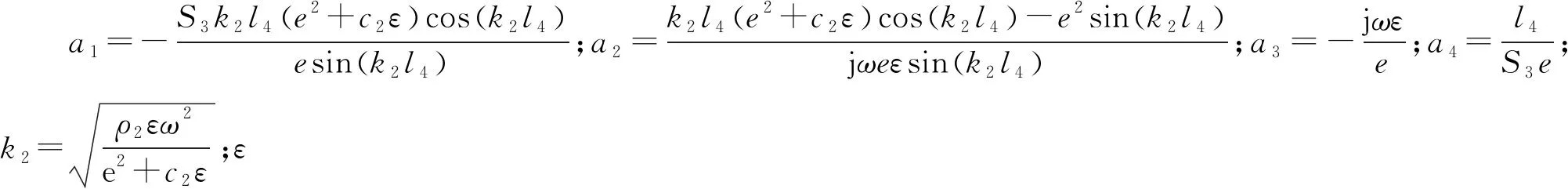
1.3 前端蓋的等效四端網絡模型

前端蓋可以看作是一小段不具備放大作用的變幅桿，故前端蓋的四端網絡模型相似于等截面變幅桿四端網絡模型。前端蓋的傳輸方程為

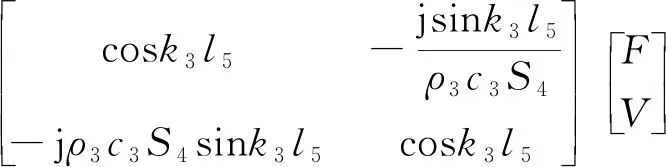
(6)

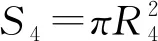
1.4 帶負載聲學系統整體理論模型建立

利用四端網絡法將超聲聲學系統的各部分結合在一起，使用ZF代表負載的統一參量。

根據圖4可得聲學系統的四端網絡傳輸矩陣模型為

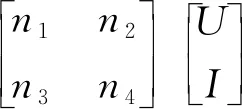
(7)

圖4 帶負載聲學系統四端網絡Fig.4 Four-terminal network with load acoustic system

為了方便計算及后面的分析，將傳輸矩陣中復數變量提取出來，令

(8)

變幅桿輸入阻抗為變幅桿的輸入端力與輸入端振速之比。參考變幅桿輸入阻抗的定義，聲學系統的輸入阻抗為

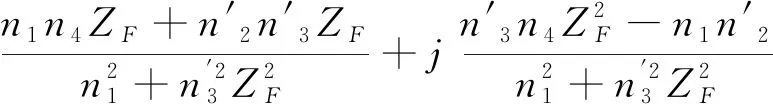
(9)

變幅桿的放大系數等于兩端面的位移或者速度之比。參考變幅桿放大系數的定義，超聲鉆削聲學系統整體放大系數的關系式為

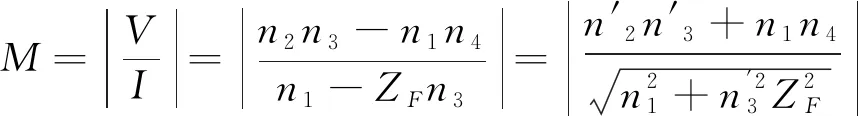
(10)

由聲學系統理論可知刀尖的瞬時位移為

S=Asin(2πft+b)

(11)

刀尖瞬時速度為

V0=S′=2πfAcos(2πft+b)

(12)

刀尖速度與振幅的關系可簡化為

V=2πfA

(13)

將式(13)帶入式(10)，得到負載、輸出振幅和輸入電流的關系式為

(14)

1.5 帶負載聲學系統數值計算及分析

確定系統的設計頻率為35 kHz,復合變幅桿的幾何參數[17]以及聲學系統中各部分的性能參數如表1所示。四端網絡參數如表2所示。

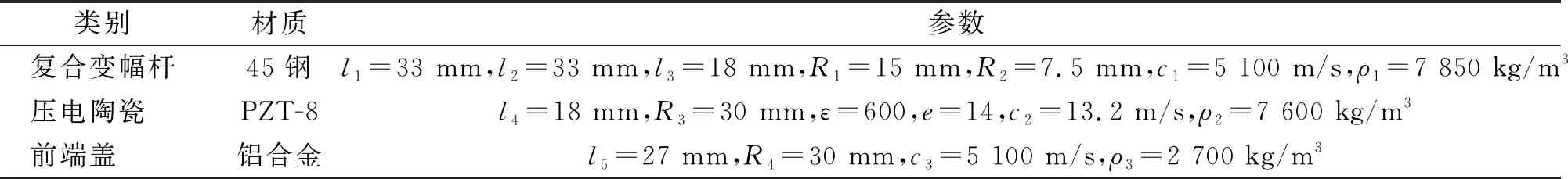
表1 聲學系統性能參數表

表2 聲學系統四端網絡參數表

Tab.2 Acoustic system four-terminal network parameter table

類別參數大圓柱段C11=0.174C12=-3.41×10-5jC13=-2.84×104jC14=0.174圓錐段C21=-0.357C22=-6.8×10-5jC23=16 951.8j-1C24=0.44小圓柱段C31=0.724C32=-9.5×10-5jC33=-4 975.9jC34=0.724復合變幅桿t1=-2.927t2=4.82×10-5jt3=-1 221.28jt4=-0.362壓電陶瓷a1=-21 764a2=-0.233ja3=-9.42×106ja4=1.819前端蓋b1=0.395b2=-9.44×10-5jb3=-8 940.04jb4=0.395聲學系統n1=1.86×108n2=0.169 5jn3=-5.76×105jn4=641.19

根據上述計算，將得到的聲學系統四端網絡參數帶入式(9)，可得輸入阻抗公式為

(15)

將聲學系統四端網絡參數帶入式(14)，可得負載、輸出振幅和輸入電流的關系式為

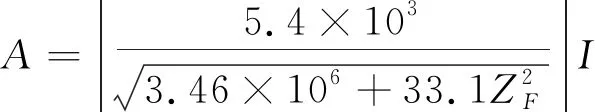
(16)

當聲學系統的調諧匹配無法進行快速響應時，系統存在靜態匹配，輸入阻抗的虛部無法被及時抵消。取輸入阻抗虛部

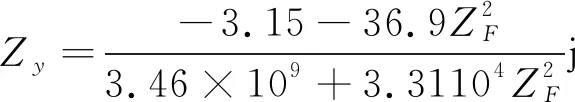
(17)

根據式(17)，用Matlab軟件作圖得到負載阻抗與輸入阻抗虛部關系如圖5所示。

聲學系統作為超聲波發生器的能量接受部分，其輸入阻抗隨負載阻抗的變化越小，接受能量就越穩定，系統的阻抗匹配與調諧匹配也就越容易完成。由圖5可知，隨著負載阻抗的增大，輸入阻抗虛部先快速增加后趨于平穩。輸入阻抗的快速變化導致使聲學系統的阻抗匹配與調諧匹配無法迅速完成，從而導致諧振頻率在系統匹配的過程中產生偏移。

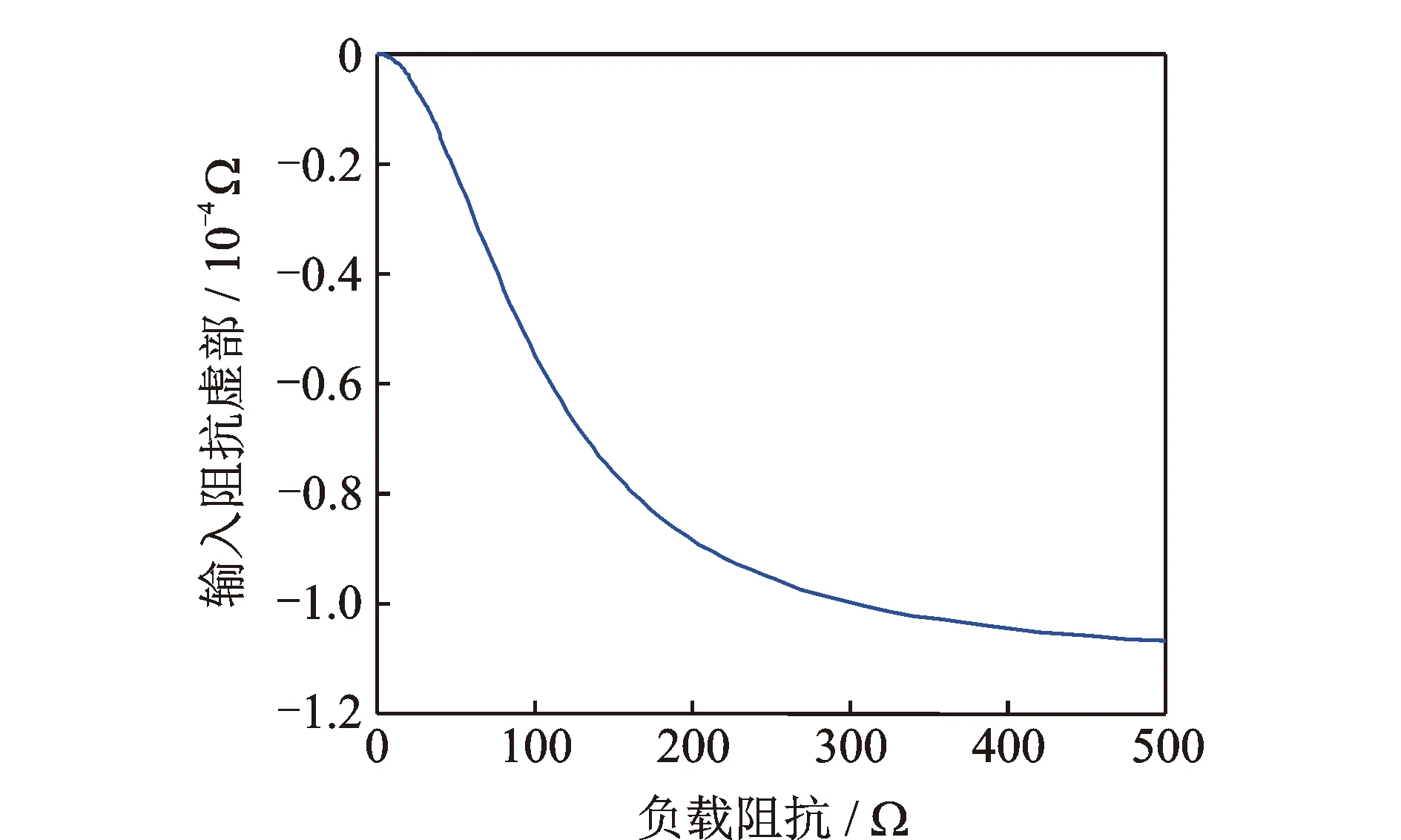
圖5 負載阻抗與輸入阻抗虛部關系圖Fig.5 Load impedance and input impedance imaginary relationship diagram

當聲學系統的調諧匹配可以隨時保持諧振時，系統存在動態匹配，則輸入阻抗的虛部一直為零，此時取輸入阻抗的實部

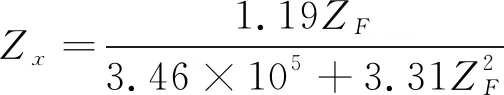
(18)

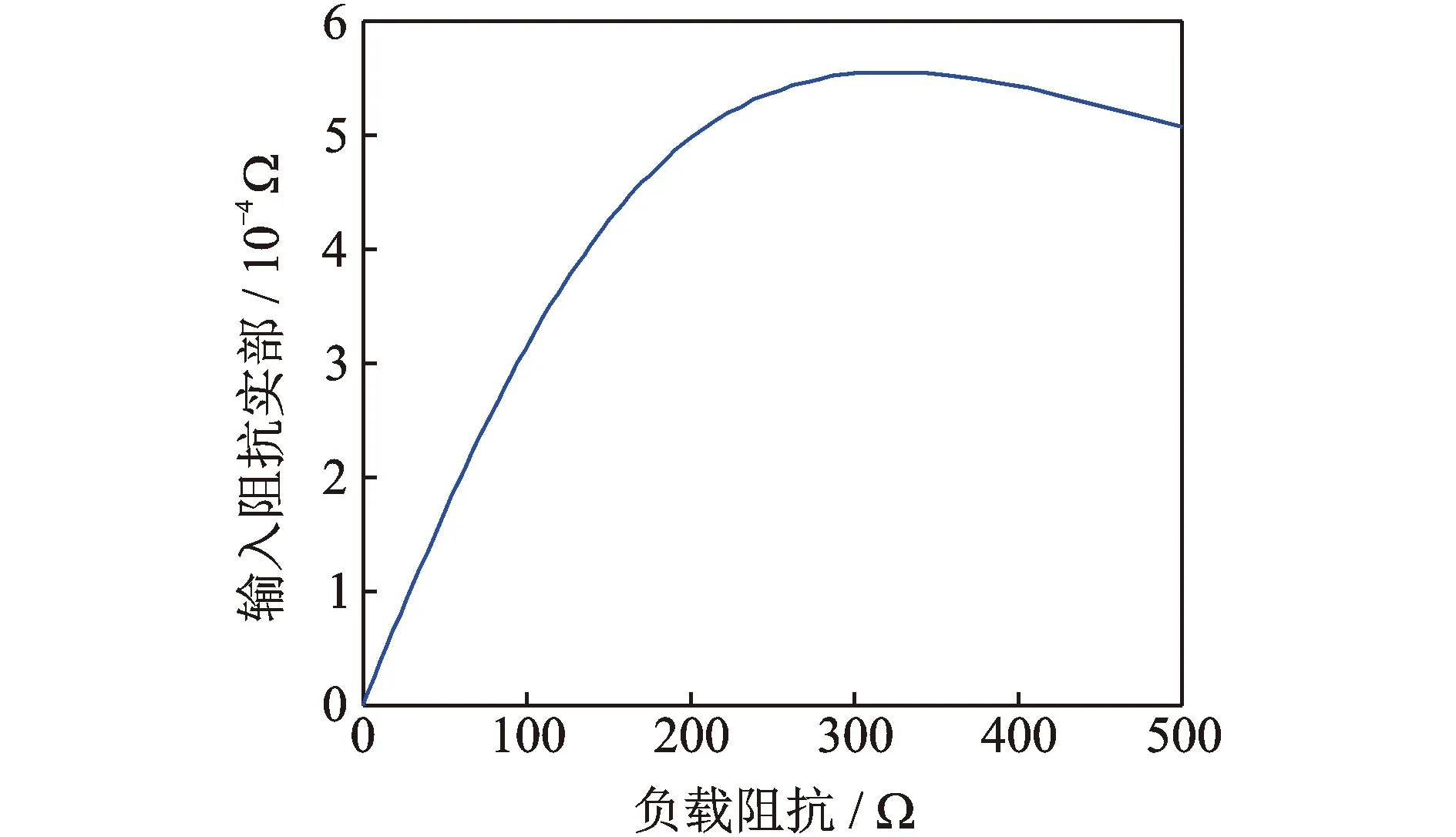
圖6 負載阻抗與輸入阻抗實部關系圖Fig.6 Load impedance and input impedance real part relationship diagram

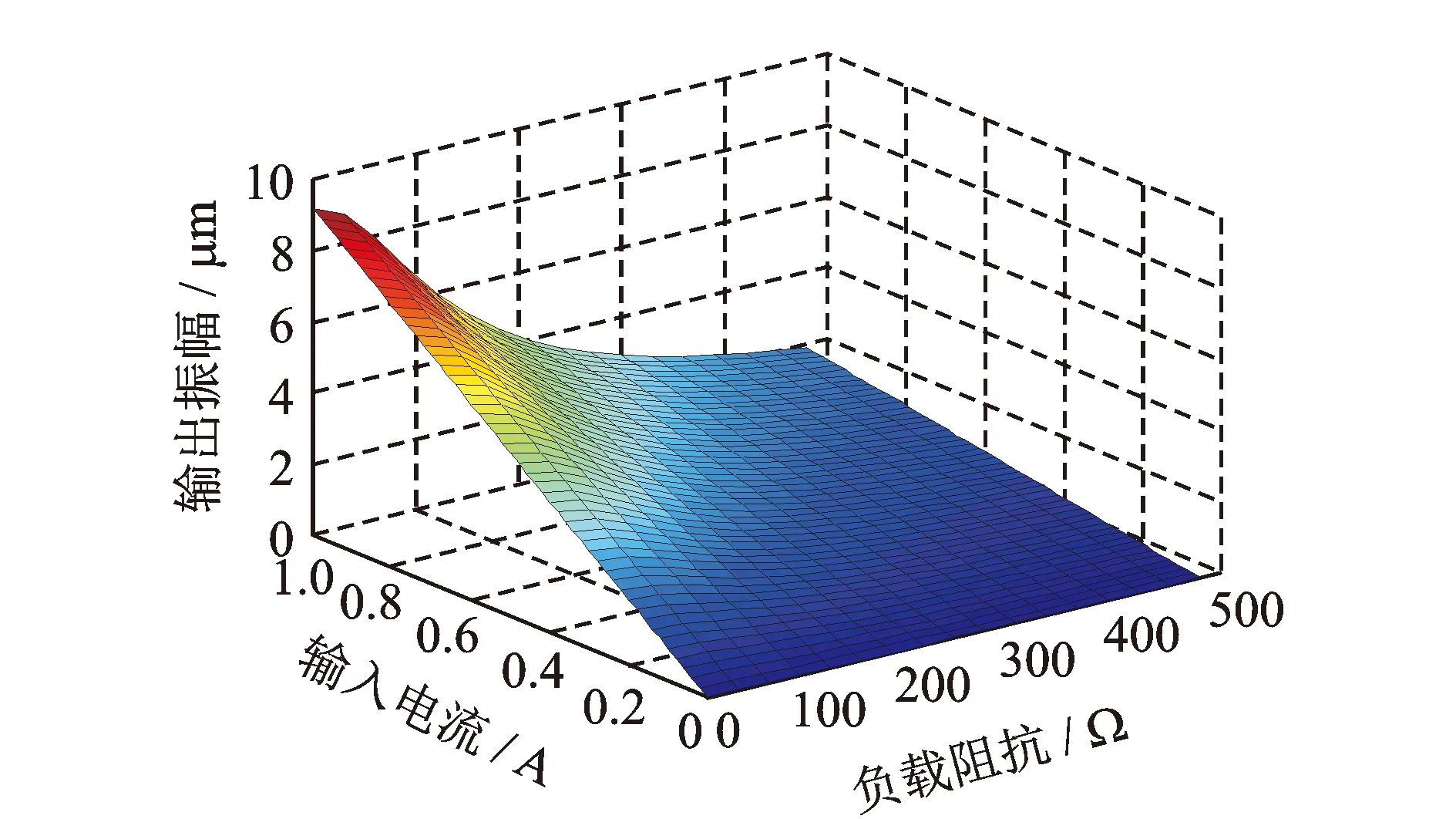
圖7 負載阻抗-輸入電流-輸出振幅關系圖Fig.7 Load impedance-input current-output amplitude relationship diagram

由式(18)利用Matlab軟件作圖得到負載阻抗與輸入阻抗實部關系如圖6所示。由圖6可知，隨著負載阻抗的增大，輸入阻抗的實部先迅速增大，隨后小幅減小。輸入阻抗的增加會使系統的損耗升高，能量傳輸效率降低，影響系統阻抗匹配的過程，從而影響系統整體的穩定性。

根據式(16)得到負載阻抗、輸入電流以及輸出振幅之間的關系如圖7所示。由圖可知，隨著負載阻抗值的增大，聲學系統的輸出振幅減小，輸入電流增大，兩者的比值逐漸減小。這說明負載阻抗越大，聲學系統的放大系數就越小。

2 帶負載超聲縱-扭復合變幅桿有限元仿真

2.1 超聲縱-扭復合變幅桿模態分析

通過理論設計35 kHz圓錐過渡型復合變幅桿，在復合變幅桿圓錐段開設3條均布螺旋溝槽，槽寬為6 mm,槽深為4 mm，螺旋角度為60°。使單向模態的縱向振動激勵實現超聲縱-扭復合振動輸出。

根據理論推導的數據進行三維建模，在復合變幅桿節點處添加6 mm厚法蘭盤，并在圓錐段開設3條均布螺旋溝槽。將模型導入分析軟件Ansys中，對其進行模態分析。材料定義45鋼，選用Workbench默認網格劃分單元，模態拓展階數為25，模態分析結果如圖8所示。由圖可知，縱-扭復合模態下的諧振頻率為34 570 Hz，與理論值偏差430 Hz。分析其原因：a.開設溝槽后，變幅桿的質量發生變化，從而影響其諧振頻率；b.螺旋溝槽結構使縱向振動轉換為縱-扭復合振動，而縱向振動與扭轉振動的波長不一樣，其諧振頻率也不相同；c.由于開設溝槽后，溝槽部分的剛性及強度減弱，施加相同的應力作用，溝槽部分的的變形量較大，即該部分材料的彈性模量E變小，而彈性模量E與波速c的平方成正比，波速c的減小會導致變幅桿諧振頻率f的變化[18]。

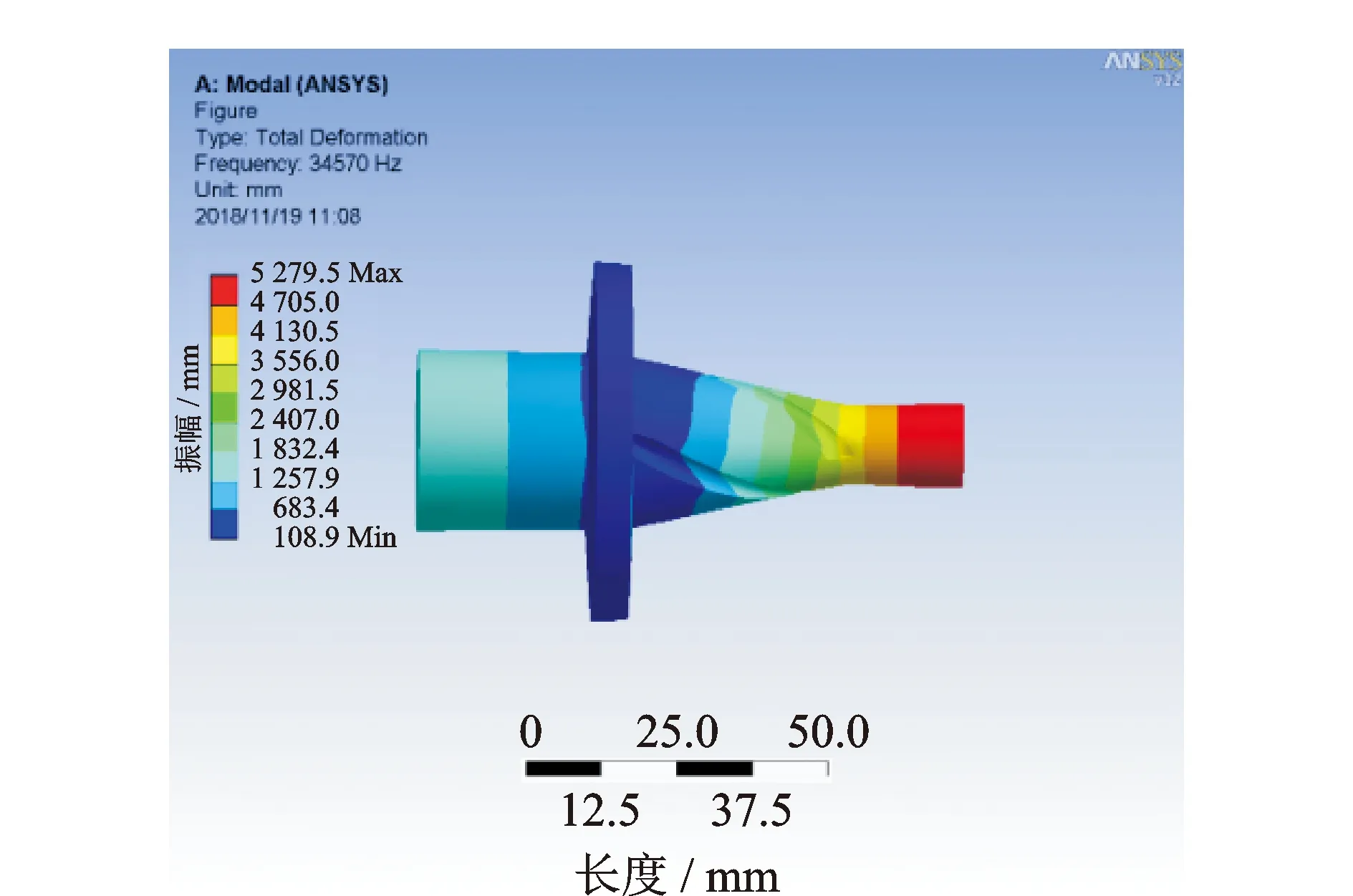
圖8 縱-扭復合變幅桿模態分析Fig.8 Modal analysis of longitudinal-torsional composite horn

2.2 超聲縱-扭復合變幅桿諧響應分析

Ansys Workbench的諧響應分析可以在模態分析的基礎上進行。設置分析的頻率范圍為0～34 570 Hz，分析數量為50個，在復合變幅桿的法蘭處施加固定約束；查閱資料可知，換能器部分可提供3 μm的振動位移，因此在換能器前端蓋與變幅桿接觸面設置正弦式變化位移3 μm。分析結果如圖9所示。由圖可知，超聲縱-扭復合變幅桿最大振幅處為變幅桿的小端面處，振幅大小為9.8 μm，相較于輸入時3 μm，放大3.27倍。這說明變幅桿的設計及螺旋溝槽的開設較為合理。

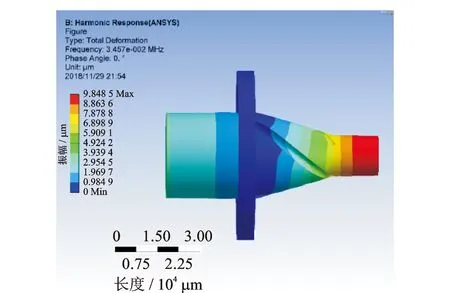
圖9 縱-扭復合變幅桿諧響應分析Fig.9 Harmonic response analysis of longitudinal-torsional composite horn

2.3 帶刀具超聲縱-扭復合變幅桿模態分析

在超聲縱-扭復合變幅桿小端處添加ER系列彈性夾頭、壓帽及直徑6 mm鉆頭，為了簡化分析，三維建模時將鉆頭簡化為直徑6 mm圓棒，模態分析結果如圖10所示。模態分析結果為34 306 Hz，相較開槽后下降264 Hz。分析其原因：a.彈性夾頭、壓帽及鉆頭通過裝配組合在一起，影響聲波的傳輸速率，波長不變聲速和頻率成正比關系，從而導致頻率有所下降；b.彈性夾頭、壓帽及鉆頭的增加使變幅桿整體長度增加，聲速不變的情況下，變幅桿半波長諧振長度增加，導致波長增加諧振頻率降低。

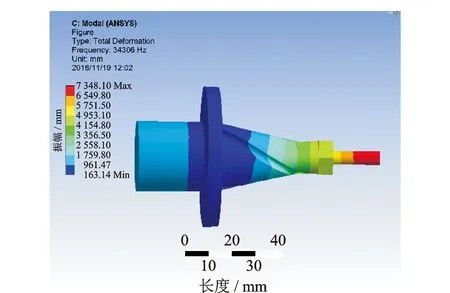
圖10 帶鉆頭縱-扭復合變幅桿模態分析Fig.10 Modal analysis of longitudinal-torsional composite horn with drill bit

2.4 超聲縱-扭復合變幅桿預應力模態分析

預應力模態分析是在模態分析之前增加靜力學分析，將靜力學分析的結果帶入模態分析里面。預應力模態分析是為了找出聲學系統受力之后的模態規律。

根據實際加工時鉆削力的大小，在鉆頭頂端施加0～500 N的軸向壓力，設置求解階數為25階，得到諧振頻率變化情況如圖11所示。由圖可知，帶刀具超聲縱-扭復合變幅桿在受到力負載后，其諧振頻率整體呈上升趨勢，但變化范圍并不大。分析原因是預應力模態分析是在模態分析的基礎上針對物體本身的結構模型進行分析的，只有當物體結構本身出現形變時，諧振頻率才會出現較大的變化。超聲縱-扭復合變幅桿在實際工作時，鉆削力對其本身結構并不會產生很大影響，但卻存在阻礙作用，抑制了聲波在聲學系統中的傳播，所以此時預應力模態分析只能反映變幅桿受力之后諧振頻率的變化趨勢。

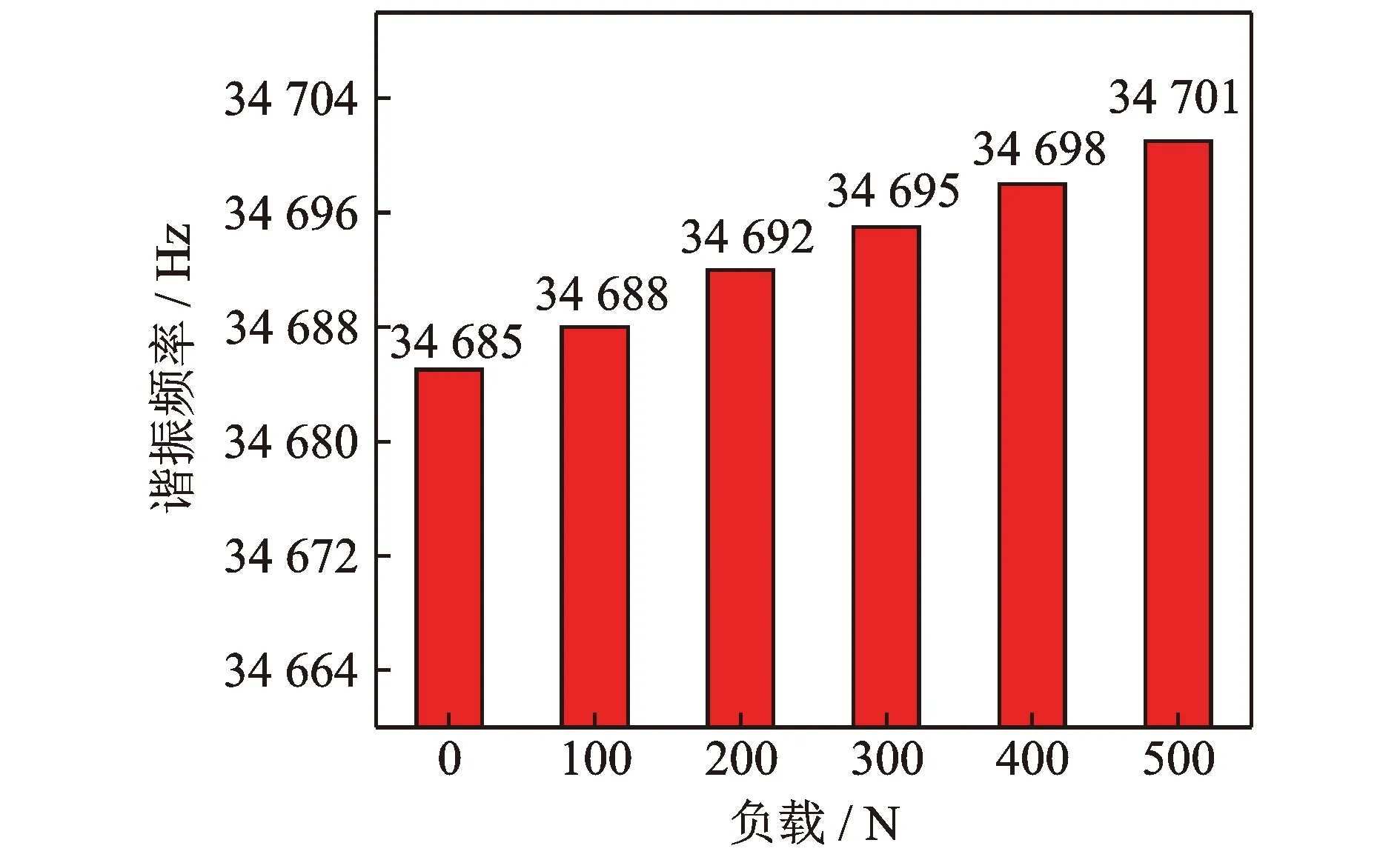
圖11 諧振頻率隨力負載變化圖Fig.11 Resonant frequency with force load change diagram

2.5 超聲縱-扭復合變幅桿瞬態動力學分析

瞬態動力學分析是時域分析，仿真物體在隨時間變化載荷作用下系統的響應過程。

聲學系統受力是周期性的，選擇5個周期作為分析對象，將一個周期分為兩個分析步，一個為力的上升過程，另一個為力的下降過程，共10個分析步。超聲鉆削聲學系統的振動頻率為35 kHz，每個分析步時間為1.4×10-5s，選擇每個分析步的分析點為10個。參考實際加工時的鉆削力，在鉆頭頂端施加500 N周期變化的軸向壓力，在變幅桿左端面施加正弦式變化位移3 μm。分析結果如圖12所示。

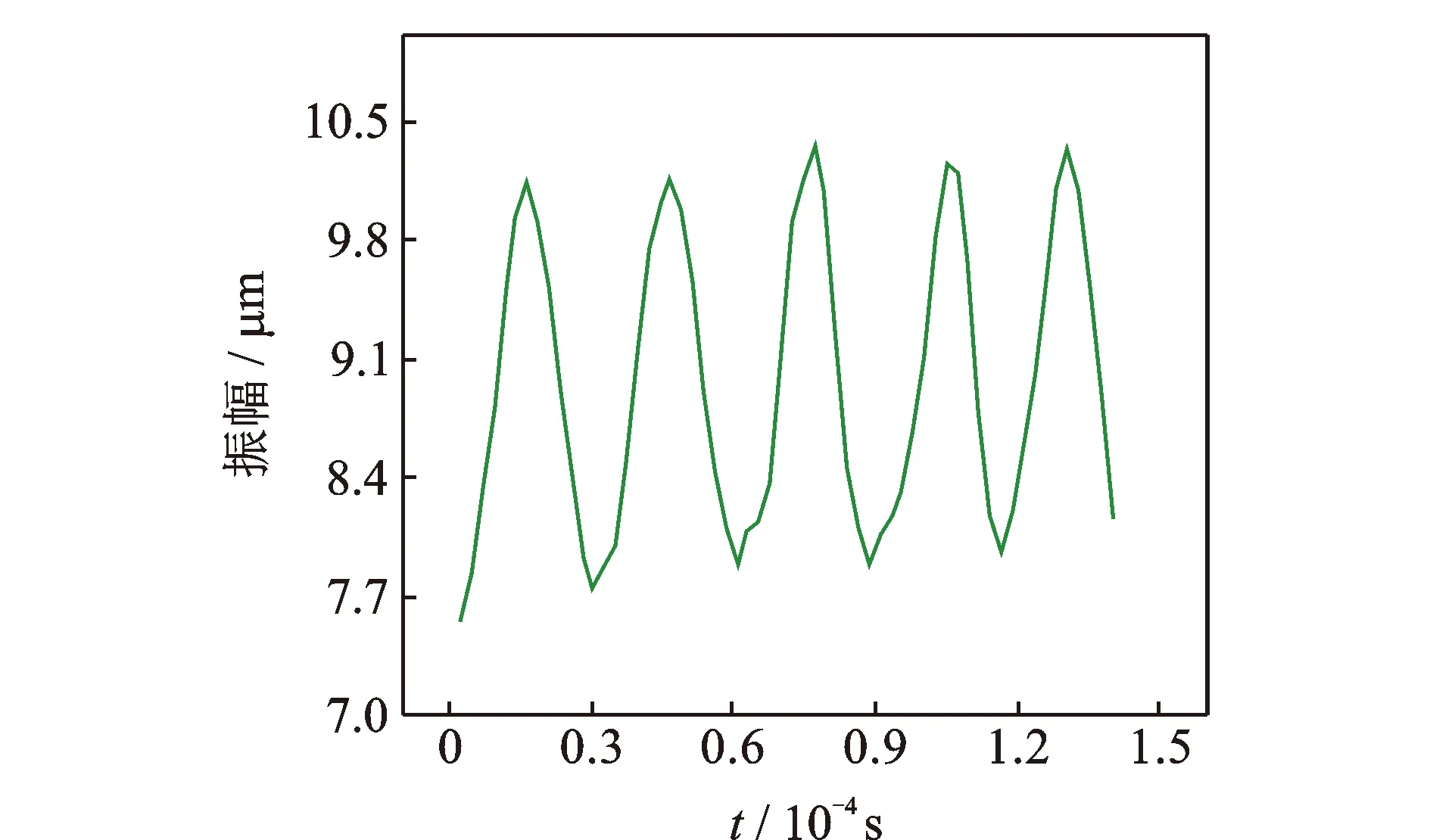
圖12 鉆頭振幅周期變化圖Fig.12 Bit amplitude period change diagram

由圖可知，在施加周期力之后鉆頭振幅隨時間的增加呈近似正弦式變化。實際加工中聲學系統的溫升問題以及動力學分析中的阻尼問題都會進一步影響鉆頭的振幅，所以在實際情況下鉆頭受力后振幅不規律變化的現象會更加突出。

3 試 驗

3.1 靜態模擬力加載試驗

模擬試驗目的在于模擬加工過程中的受力情況，以及實際加工過程中振幅難以測量的情況。試驗設計在萬能工具銑床(X8130)上進行，試驗裝置示意如圖13所示。超聲振動系統由超聲波發生器、無線傳輸系統、換能器、縱-扭復合變幅桿和鉆頭組成；在銑床主軸上裝夾的工具桿末端開設階梯孔，一面與鉆頭相接觸，激光位移傳感器(Keyence LK-G10)透過孔的另一面測量鉆頭的振幅。通過升降銑床工作臺使工具桿與鉆頭接觸，實現不同負載的施加；測力儀(Kistler-9257B)、電荷放大器(Kistler-5070A)和計算機用于實現負載的精確測量。試驗現場如圖14所示。

3.2 數據分析

記錄不同負載下超聲波發生器所追蹤的聲學系統諧振時的電流和頻率值，以及激光位移傳感器所測的振幅值，以此分析力負載對系統特性的影響。試驗選取3組實際加工中適用的電流值與其對應的諧振頻率作變量。試驗參數如表3所示。

每個測試點測試3次后取其平均值，每組試驗進行3次。采用單因素法，在頻率保持不變情況下分別測得負載對電流和振幅的影響情況如圖15，16所示。由圖15可知，隨著負載的增加電流都呈現上

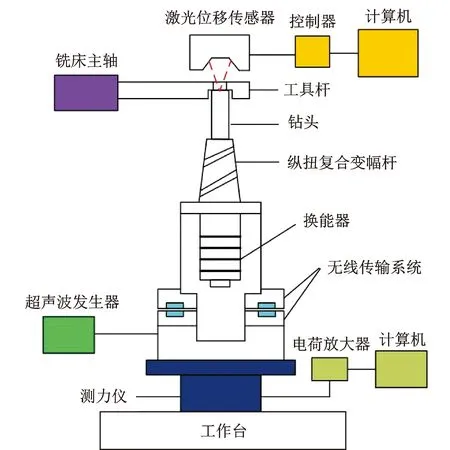
圖13 試驗裝置示意圖Fig.13 Test device schematic

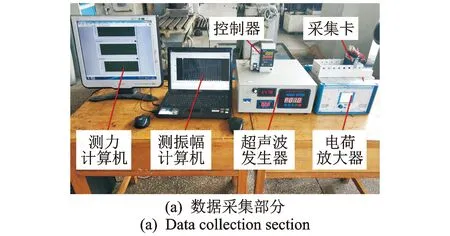
圖14 力加載試驗現場Fig.14 Force loading test site

項目試驗參數諧振頻率/kHz34.6134.3234.13I/A0.10.20.3

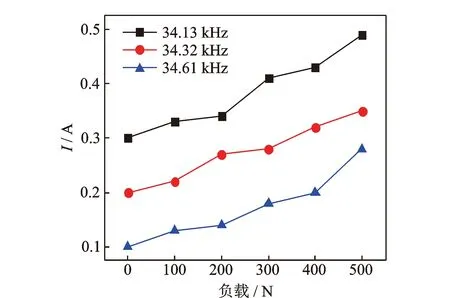
圖15 不同頻率下負載對電流的影響Fig.15 Effect of load on current at different frequencies

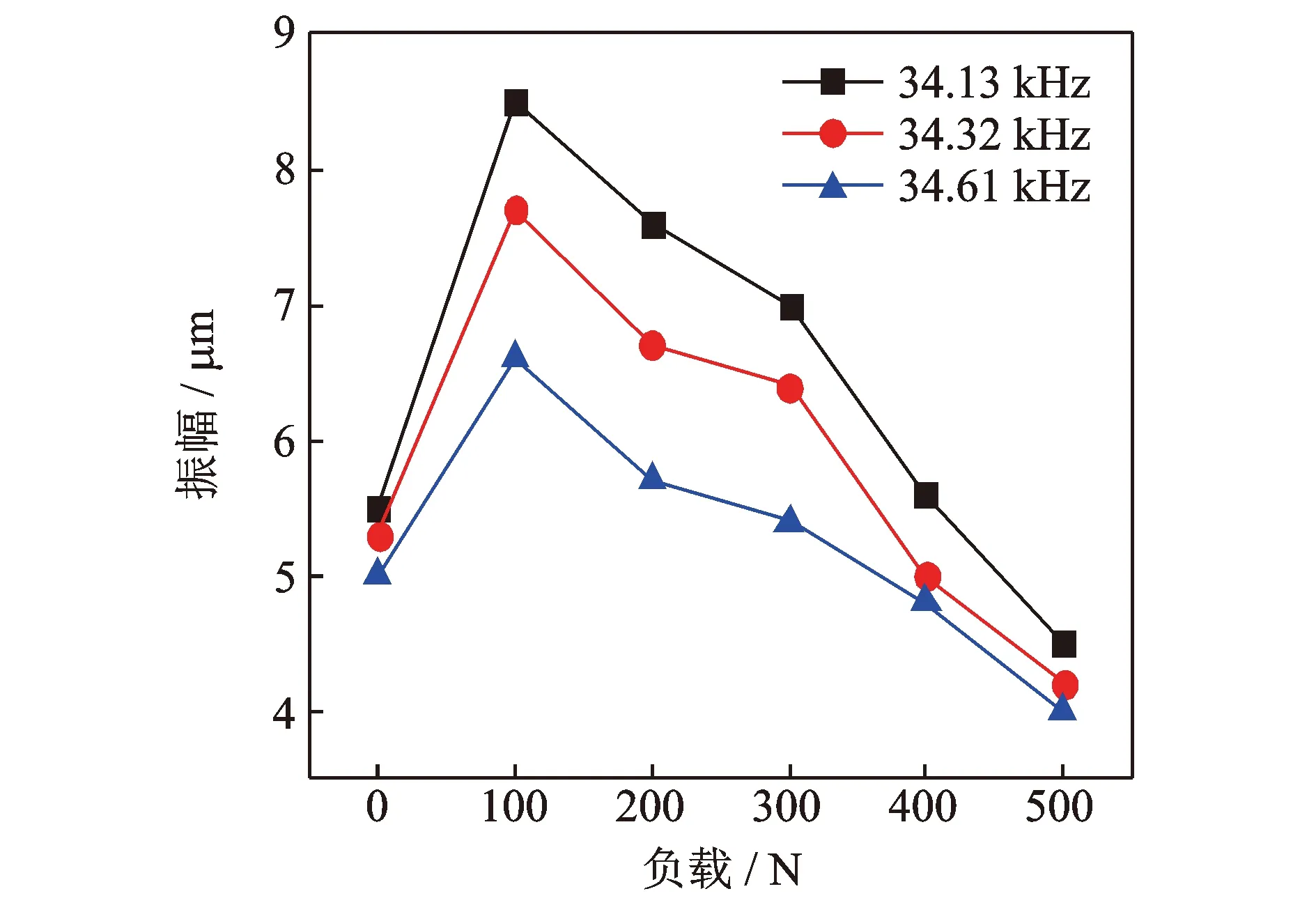
圖16 不同頻率下負載對振幅的影響Fig.16 Effect of load on amplitude at different frequencies

升趨勢，負載為500 N時的電流相較于空載時分別增加63.3%，75%及180%。電流的過大會導致系統處于高損耗、高溫度的工作狀態，影響系統的穩定性。

由圖16可知，振幅隨著負載的增加呈現先升高后下降的趨勢，當力負載大于400 N后，三者振幅均小于各自空載時的振幅。分析其原因：a.在力增加時，電流迅速增加，系統的輸出功率會在短期內快速增加，因此振幅會在前期迅速增大；b.由上文理論推導可知，系統輸入阻抗隨著負載的增加而增大，系統損耗也隨之增大，造成系統能量衰減；且電流的增大會使系統的放大系數減小，所以振幅會在后期逐漸減小；c.當施加的負載過大時，工具桿對鉆頭振動的抑制也會使得激光位移傳感器測得的振幅減小。

按照前述試驗方法，保持電流不變，記錄不同負載下超聲波發生器追蹤頻率的變化。測得負載對頻率的影響情況如圖17所示。由圖可知，隨著負載的增加，諧振頻率呈現上升趨勢，上升幅度在500 Hz左右，較仿真時有大幅增加。原因為仿真時未考慮系統的溫升和超聲波發生器自身的追頻特性，以及測量過程中的誤差。這說明負載的增加會使系統的諧振頻率產生偏移，影響系統調諧匹配的過程。

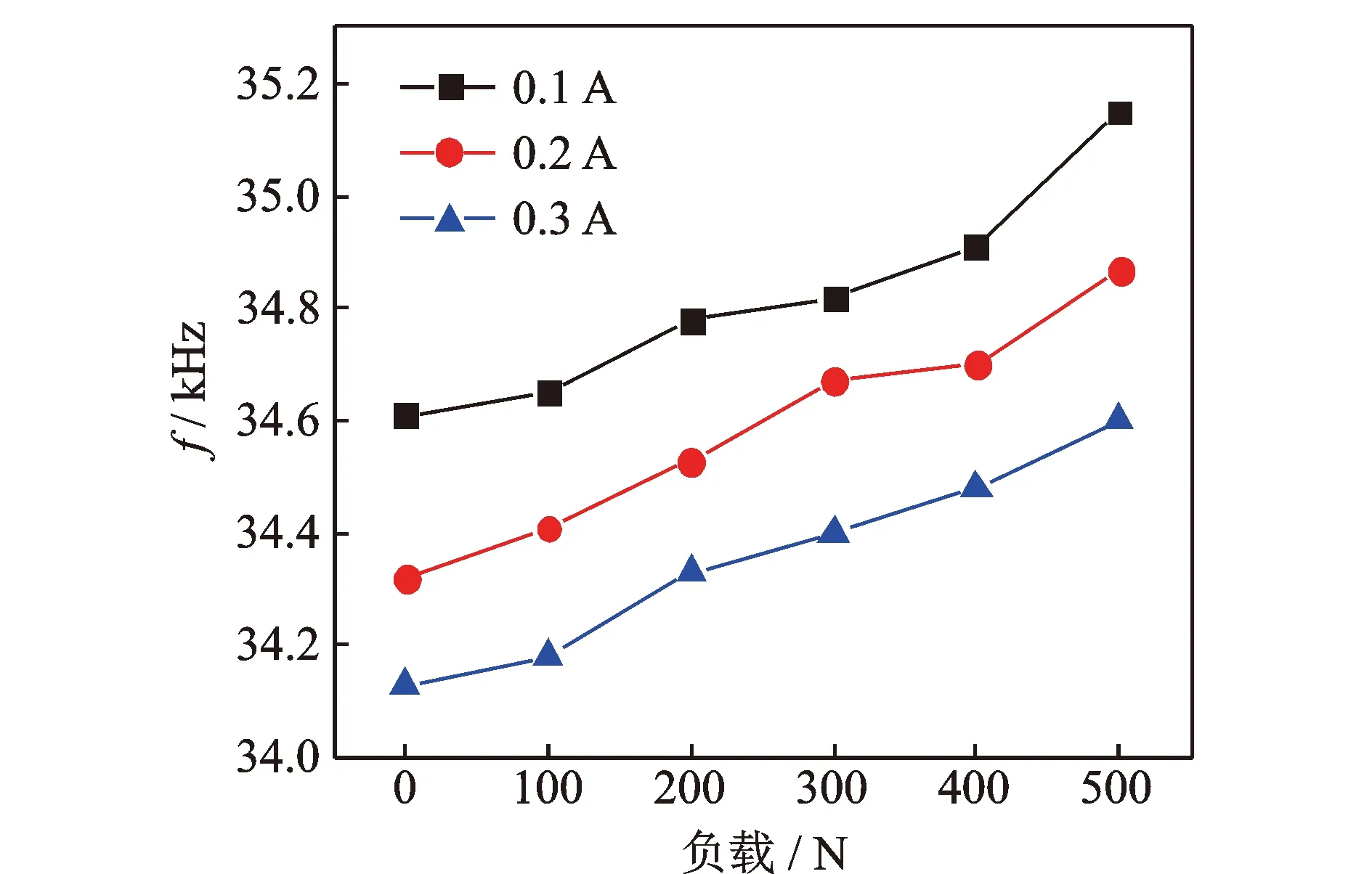
圖17 不同電流下負載對頻率的影響Fig.17 Effect of load on frequency at different currents

圖18 鉆削加工試驗現場Fig.18 Drilling test site

綜上可知，當負載大于400 N后，電流和頻率偏移過大，振幅衰減至空載時振幅以下，使聲學系統無法正常工作，故實際加工中應避免大負載的出現。

3.3 實際鉆削加工試驗

試驗平臺搭建在VMC850E立式加工中心上，工件選用Ti6Al4V鈦合金，鉆頭為直徑6 mm硬質合金鉆頭，試驗現場如圖18所示。通過虎鉗將工件固定在加工中心工作臺上，測力儀固定在虎鉗下方，超聲波刀柄及電磁感應盤固定在主軸上。

分別保持主軸轉速和進給速度一定情況下，測得進給速度和主軸轉速增加對鉆削力的影響如圖19所示。頻率為34.26 kHz,電流為0.31 A，每組數據測量3次取平均值。

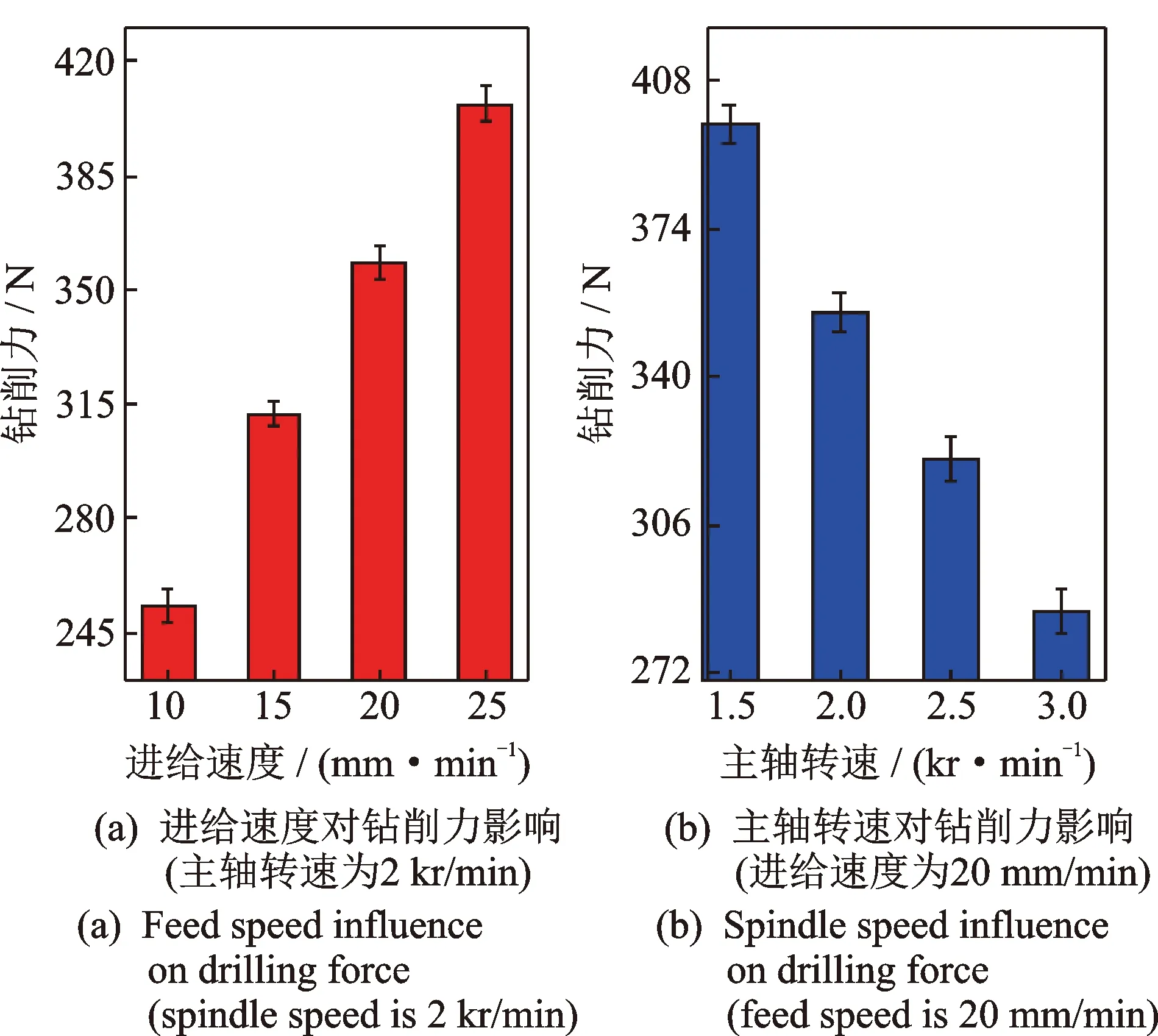
圖19 進給速度和主軸轉速對鉆削力影響圖Fig.19 Feed speed and spindle speed influence on drilling force

在給定的試驗條件和參數范圍內，進給速度每增加5 mm/min，鉆削力增加50 N左右。主軸轉速每增加500 r/min，鉆削力下降40 N左右。可見，進給速度對鉆削力的影響略大。

在主軸轉速為2 kr/min時，系統諧振頻率和電流隨進給速度增加的變化情況如圖20所示。由圖可知，在系統自動匹配過程中保證電流和頻率可變的情況下，電流增加了41.9%，頻率下降了210 Hz。分別在不同轉速、進給速度和超聲參數下加工鈦合金工件，記錄聲學系統的工作狀態。當電流增幅超過60%、頻率變化超過350 Hz時，聲學系統會出現明顯的失諧現象，超聲波發生器無法準確地搜索到系統諧振頻率，超聲輔助加工效果明顯降低。

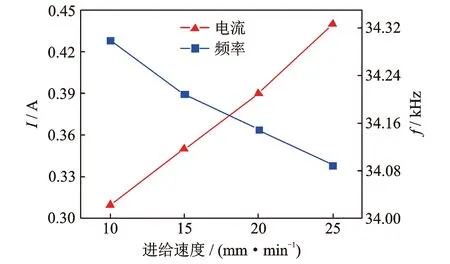
圖20 不同進給速度下頻率和電流變化情況Fig.20 Frequency and current changes at different feed rates

模擬試驗和鉆削加工試驗表明，力負載變化對系統參數及工作狀態影響明顯，是導致系統失諧、鉆頭振幅波動和系統穩定性衰減的主要因素。因此，為使超聲輔助作用達到最優，在實際加工中必須合理選擇加工工藝和加工參數，以及合理的冷卻措施，避免負載大幅度變化及大負載的出現。

4 結 論

1) 通過對整體理論模型進行參數化分析，得出隨著力負載的增加，聲學系統的輸入阻抗增加、電流上升、諧振頻率產生偏移，以及系統放大系數減小的結論。

2) 基于有限元仿真，得到諧振頻率隨靜態力增加而升高的變化規律，并發現周期力負載的施加會使系統振幅產生一定波動，其幅度達到13%。

3) 本系統在試驗中發現，當力負載大于400 N時，系統諧振時的電流和頻率會產生較大偏移，振幅急劇降低。超聲輔助鉆削鈦合金加工中，當電流增幅超過60%，頻率變化超過350 Hz時，聲學系統會出現明顯的失諧現象，從而無法正常工作。在實際加工中應合理選擇加工方案和參數，降低力負載對系統穩定性的影響。該結果為研究超聲振動系統的穩定性以及超聲輔助鉆削加工提供了指導和借鑒。