基于半互功率譜密度及響應面法的干氣密封系統工作模態分析

劉 蘊， 劉全興， 殷 鳴， 殷國富,

(1．四川大學 空天科學與工程學院，成都 610065；2.四川航天職業技術學院 飛行器制造系，成都 610100；3.四川大學 制造科學與工程學院，成都 610165)

隨著機械密封的不斷發展，干氣密封以其低磨損、低泄漏等優點逐漸成為多個工業領域高參數(高轉速r和高壓力p)操作條件下的軸封首選，但是在高參數條件下，特別是高轉速條件下，干氣密封系統極有可能發生劇烈振動導致密封失穩甚至失效，因此對于干氣密封整體系統動態特性的研究顯得尤為重要。系統動態特性的研究方法主要包括試驗狀態模態分析和工作狀態模態分析(Operational Modal Analysis, OMA)，試驗試態模態分析是在人工激勵下完成的模態分析，其激勵和響應均為已知[1]。然而對于一些復雜的機械結構(海洋平臺、橋梁和大型建筑等)來說，難以采用人工激勵的方式使其產生振動，還有一些特殊裝置，如干氣密封裝置，只有在工作狀態下才可形成完整的系統特性，這就需要在自然工作環境激勵下測得響應從而進行模態分析完成模態識別，即工作狀態模態分析。相比于試驗狀態模態分析，工作狀態模態分析不需要特定的試驗條件，被測試結構可以正常使用，直接獲得其工況狀態特性，提高了試驗效率和實用性[2]。自20世紀70年代起，石油產業、汽車工業以及航天領域都開始對環境激勵下的工作模態分析進行研究[3-4]，Bonato等[5]采用自相關和互相關的方法來識別未知激勵下模態參數，且指出基于互相關方法能抵抗噪聲干擾；申凡等[6]將互功率譜運用于多參考點頻域方法中，用各測點的互功率譜代替頻響函數獲得了振型，彌補了多參考點復指數法的不足；申凡等[7]提出利用互功率譜密度代替功率譜分析，以此來解決模態識別分析的局限性和非線性問題；鄭敏等[8]對時域工作模態復指數法和頻域工作模態識別法進行了試驗比較，得到了頻域工作模態識別法比時域工作模態復指數法識別精度更高；樓江雷等[9]和趙峰等[10]均基于LMS Test. Lab 9A軟件及采集儀實現了工作模態實驗，采用最小二乘復頻域法完成了對實驗裝置各階模態的參數識別；李晰等[11]采用FDD法對鋼管混凝土拱橋的工作模態進行識別，準確識別出了實際結構的前5階模態，取得了良好的識別效果。

本文采用多參考點最小二乘復頻域方法，分別利用互功率譜函數(Cross Power Spectra)和半互功率譜密度函數(Cross Half Power Spectra Density/Cross Half PSD)實現對干氣密封裝置的工作狀態模態分析[12]，在不同轉速與介質壓力條件下完成對干氣密封裝置的環境激勵工作模態參數識別；采用平均相位偏差(Mode Phase Deviation, MPD)、模態相位線性度(Mode Phase Collineation, MPC)、模態復雜性(Mode Complexity, MOV)和模態指示函數(Mode Indication Function, MIF)等數學指標進行兩個函數的模態分析結果進行驗證，防止因噪音干擾、激勵不充分等造成的算法魯棒性不強而形成虛假模態[13]；驗證結果表明：半互功率譜密度函數相比于互功率譜函數的模態分析結果更為穩定，模態驗證效果更佳，更加適合于此類干氣密封組合型裝置的環境激勵工作狀態模態分析，模態分析結果表明：操作條件中轉速對于系統模態的影響大于介質壓力，并且對于不同方向不同階次的影響程度不同。基于響應面方法與模態分析結果，以不同的操作條件(介質壓力p與轉速r)、方向D和模態階數N為響應面變量，建立干氣密封系統多工況下模態參數的完整二次多項式工作模態響應面模型并驗證了模型的有效性，為實現時變模態的辨識提供了新的方法并為后續系統模態深入研究奠定了基礎。

1 互功率譜與半互功率譜密度函數理論

工作狀態模態分析方法是利用輸出響應的譜函數近似代替頻響函數來實現模態識別，在實際工程中，對結構系統進行模態分析和參數識別時，可假設結構具有N階模態，L個激勵滿足白噪聲平穩條件，那么在點l激勵下結構上點m和點n的互功率譜函數Gmnl(jw)可以表示為

(1)

式中：Gffl(jw)為點l處激勵f的自功率譜函數，在白噪聲輸入下，其與頻率無關，可用常數C表示，那么式(1)可寫為

(2)

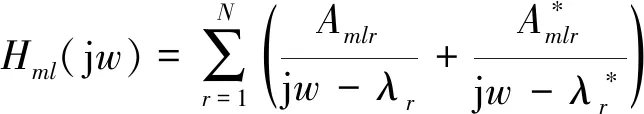
(3)

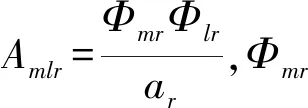
將式(3)代入式(2)可得

(4)

式(4)可分解為

Gmnl(jw)=

(5)

(6)

考慮所有的激勵點可得

(7)

(8)

式中：

(9)

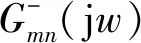
2 環境激勵的干氣密封振動測試試驗

2.1 試驗設計

干氣密封裝置是主要的軸封裝置，屬于多零部件組合系統，軸長約80 cm，端面直徑為90 cm，結構如圖1所示。密封運行時，動環嵌套在軸套中，隨軸一起轉動(引入轉速r)，從而引入高壓氣流(引入介質壓力p)進入密封槽推開浮動環，形成高壓密封氣膜，其中彈簧座固定，彈簧始終處于壓縮狀態使得浮動環與推環始終貼合運動[17-18]。當外界或裝置本身產生一定激振時，在激振頻率ω接近系統固有頻率f時，系統會發生共振，打破平衡的配合關系從而影響密封可靠性和穩定性，為獲得干氣密封模態參數，只能采用環境激勵工作狀態模態分析法。

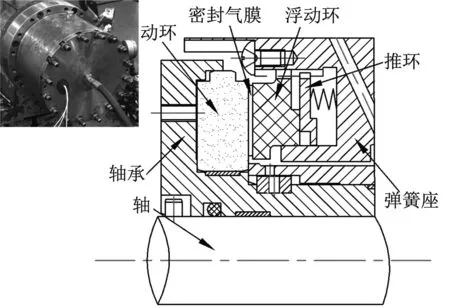
圖1 干氣密封結構示意圖

根據干氣密封裝置的結構特點，模態實驗設計20個測點，20個ICP加速度傳感器(型號：333B30，靈敏度：100 mV/g，頻率范圍：0.5 Hz～3 kHz，量程：50g，重量：3 g)分別以軸向、徑向和周向形式均勻布置于密封整機之上，具體分布如圖2所示。為得到系統多階模態參數值，傳感器布置個數最好為所需階數兩倍以上，傳感器粘貼位置應盡量靠近構件結合面處，以防測得單個構件模態。由密封廠提供的工況控制平臺確保工作條件穩定，以盡量滿足平穩輸入條件，采用M+P Smart Office測試系統，以1點為參考點Excitation，每次平穩測試時間為300 s，采樣頻率為2 048 Hz，采樣點為4 096個，建立整機簡化Geometry(見圖3)模型以獲取振型。

在干氣密封工況條件中，軸轉速r與介質壓力p為兩個重要的操作參數，兩者變化均會一定程度影響密封氣膜動態特性[19]，也會一定程度上影響構件結構特性，所以在干氣密封運行過程中，尤其是開機、停機過程，其軸轉速r與介質壓力p會發生變化導致動態特性實時變化，這就要測試不同操作條件下干氣密封系統的模態參數。依據所提供的干氣密封工況額定操作條件值(轉速r與介質壓力p)，軸向、徑向和周向試驗測試設計為表1所示。試驗步驟為:

圖2 試驗測點布置

圖3 系統簡化模型

步驟1 在額定介質壓力分別為1 MPa、2 MPa和3 MPa時，測試轉速為4 000 r/min、6 000 r/min和8 000 r/min工況條件下20個測試點的振動響應；

步驟2 基于M+P Smart Office編程軟件，采用多參考點最小二乘復頻域方法(PolyLSCF)分別以互功率譜和半互功率譜密度作為擬合函數，整體估計極點和模態參預因子；

步驟3 建立穩態圖，獲得系統固有頻率值和振型。

2.2 試驗結果

從干氣密封工況要求與失效經驗出發，主要研究低于1 000 Hz模態。分別運用測試點之間的互功率譜函數(Cross Power Spectra)與半互功率譜密度函數(Cross Half PSD)采用多參考點最小二乘復頻域方法求得各階模態，以轉速4 000 r/min為例，結果分別如表2(a)、表2(b)、表2(c)、表3(a)、表3(b)和表3(c)所示。

2.3 試驗驗證

在完成環境下的模態識別后，要對結果進行模態驗證以剔除虛假模態。先利用頻率與振型是否合理正確進行初步模態篩選，再利用模態置信度(Modal Assurance Criterion, MAC)、平均相位偏差(MPD)、模態相位線性度(MPC)、模態復雜性(MOV)以及模態指示函數(MIF)進行模態最終驗證。

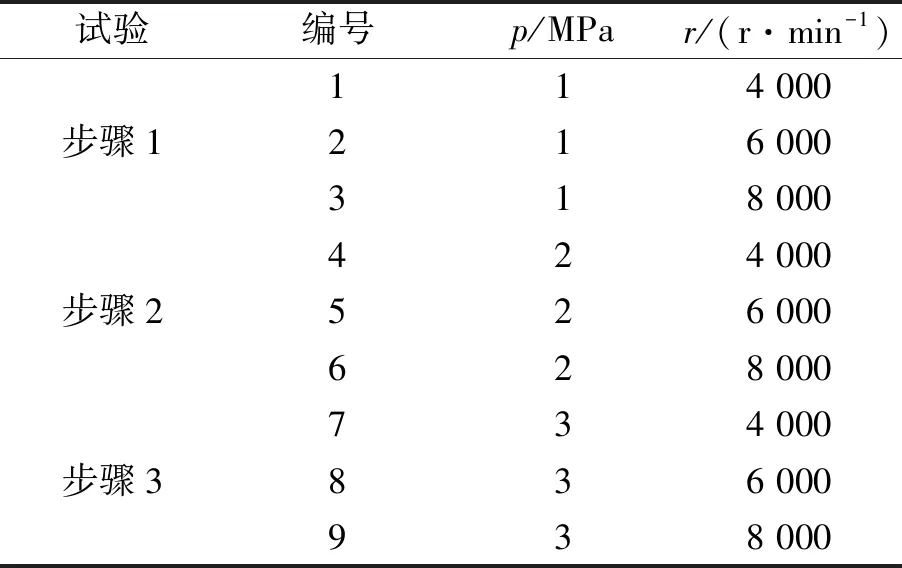
表1 系統測試試驗設計

表2(a) 軸向-Cross Power Spectra函數模態分析結果

Tab.2(a) Axial-Cross Power Spectra function modal analysis results

階次1 MPa-4 000r/minf/Hz2 MPa-4 000r/minf/Hz3 MPa-4 000r/minf/Hz166.769.669.72133.6139.6139.93351.7209.5207.14395.9347.3353.85547.8554.2544.06600.0606.8606.07697692695

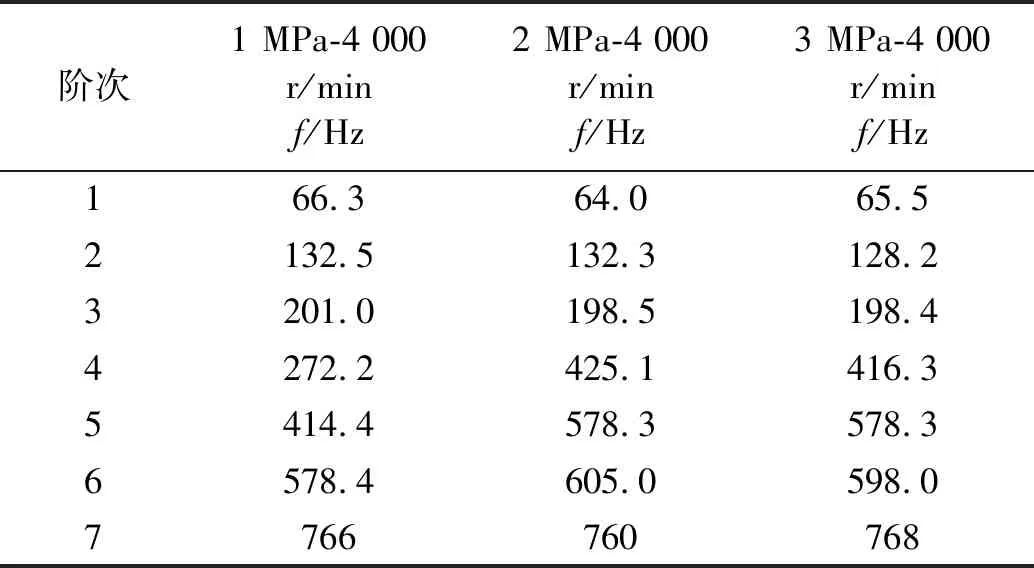
表2(b) 徑向-Cross Power Spectra函數模態分析結果

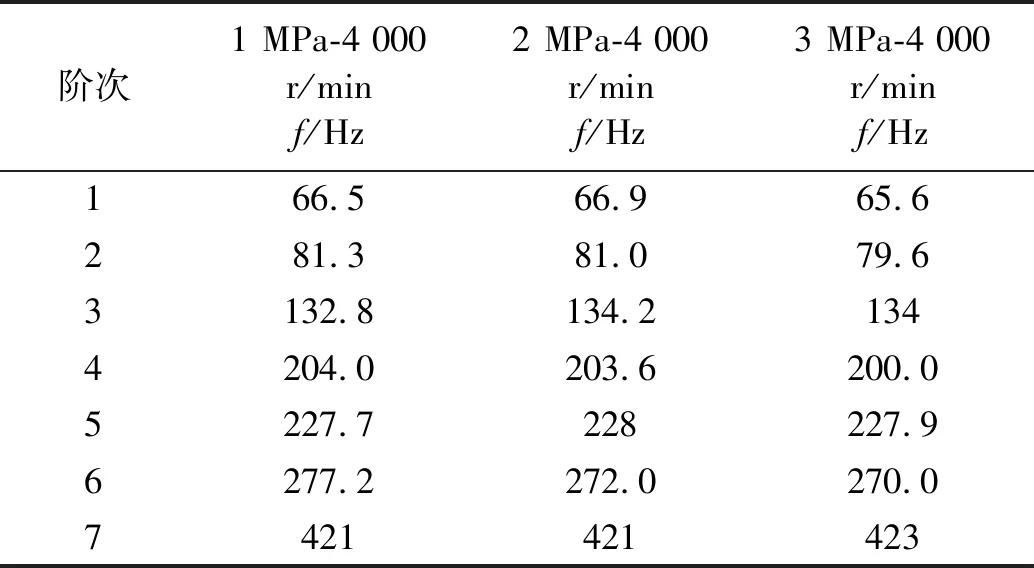
表2(c) 周向-Cross Power Spectra函數模態分析結果

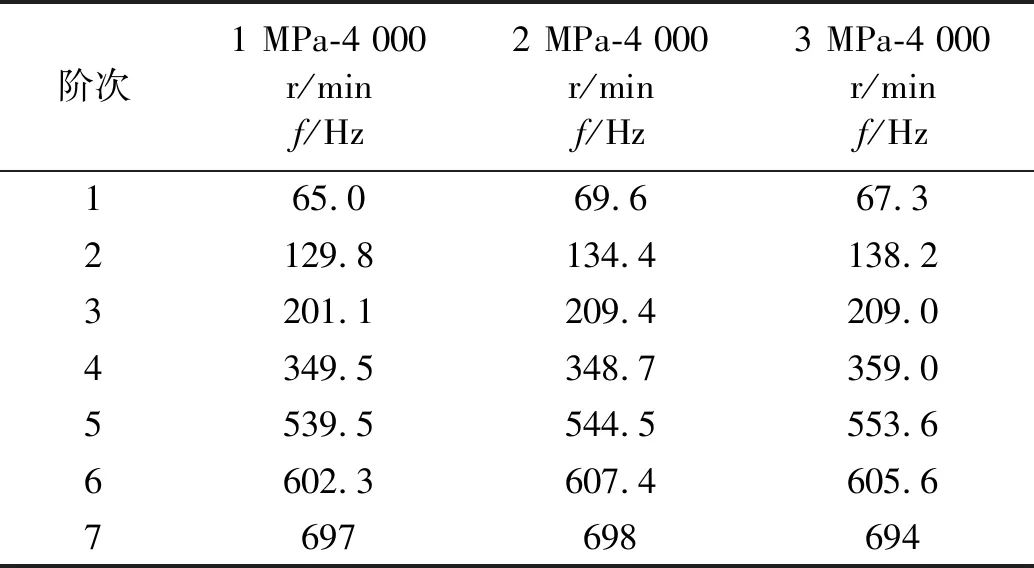
表3(a) 軸向-Cross Half PSD函數模態分析結果

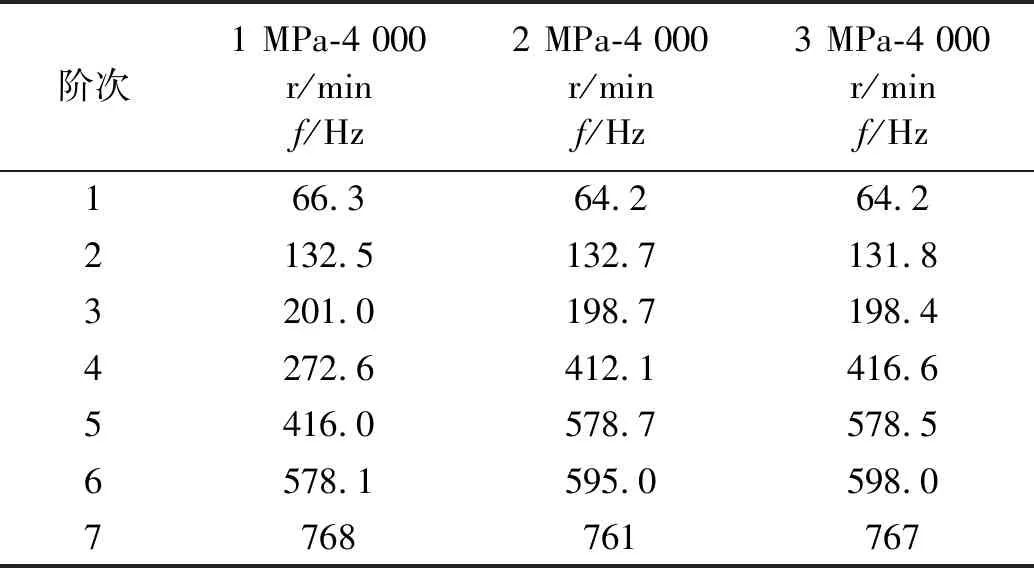
表3(b) 徑向-Cross Half PSD函數模態分析結果

表3(c) 周向-Cross Half PSD函數模態分析結果

Tab.3(c) Circumferential-Cross Half PSD function modal analysis results

階次1 MPa-4 000r/minf/Hz2 MPa-4 000r/minf/Hz3 MPa-4 000r/minf/Hz168.365.465.6281.880.681.23132.5135.4134.24229.9227.6202.45264.6262.0228.36425423423

對于干氣密封這種旋轉部件來說，在工作模態測試中，實際環境中的轉動會形成激振，此激振會形成諧振導致出現極點峰值，這就需要一個去除與轉速相關激振頻率值的過程。以1 MPa-4 000 r/min軸向測試結果為例，試驗結果中，接近66.6 Hz、133.3 Hz和200.0 Hz等以上為66.6 Hz倍數的頻率值均需驗證，通過頻率與振型合理性可知，表2(a)中的66.7 Hz、133.6 Hz、395.9 Hz和600.0 Hz，表3(a)中的65 Hz、129.8 Hz、201.1 Hz和602.3 Hz均為激振頻率應剔除；如圖4所示，頻率值與振型均符合模態特性。351.7 Hz(a)和349.5 Hz(b)的振型為沿軸向左右擺動;547.8 Hz(c)和539.5 Hz(d)的振型為沿軸向前后擺動;697 Hz(e)和697 Hz(f)的振型為沿軸上下移動并左右擺動。

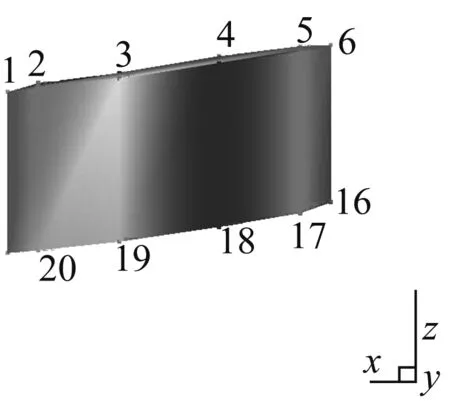
(a)

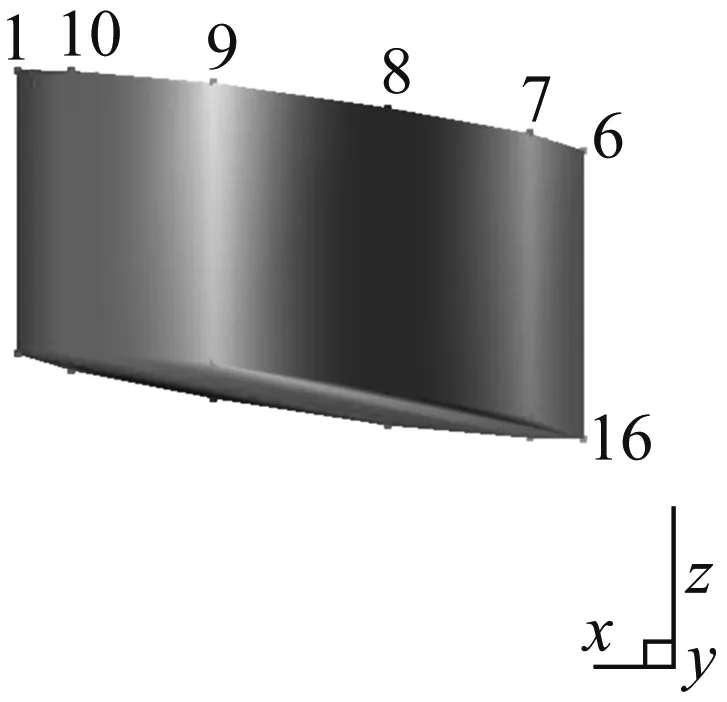
(b)

(c)

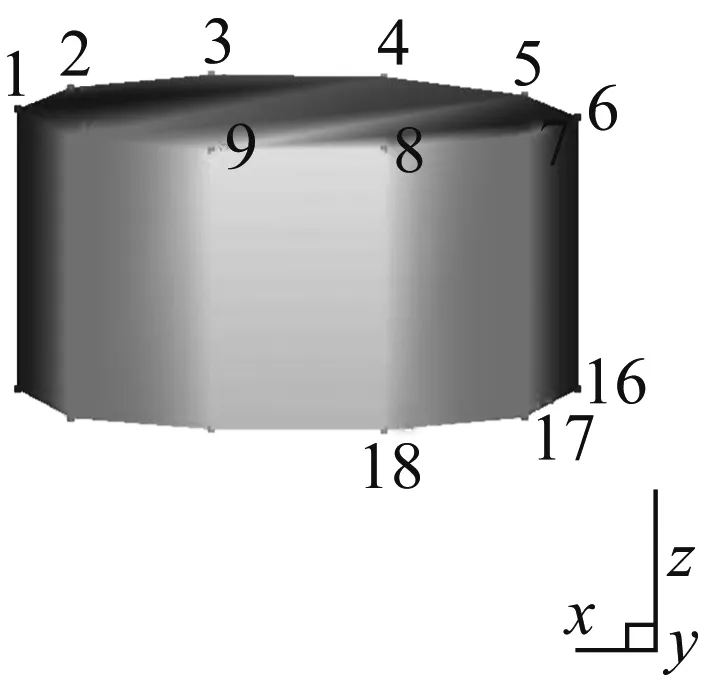
(d)

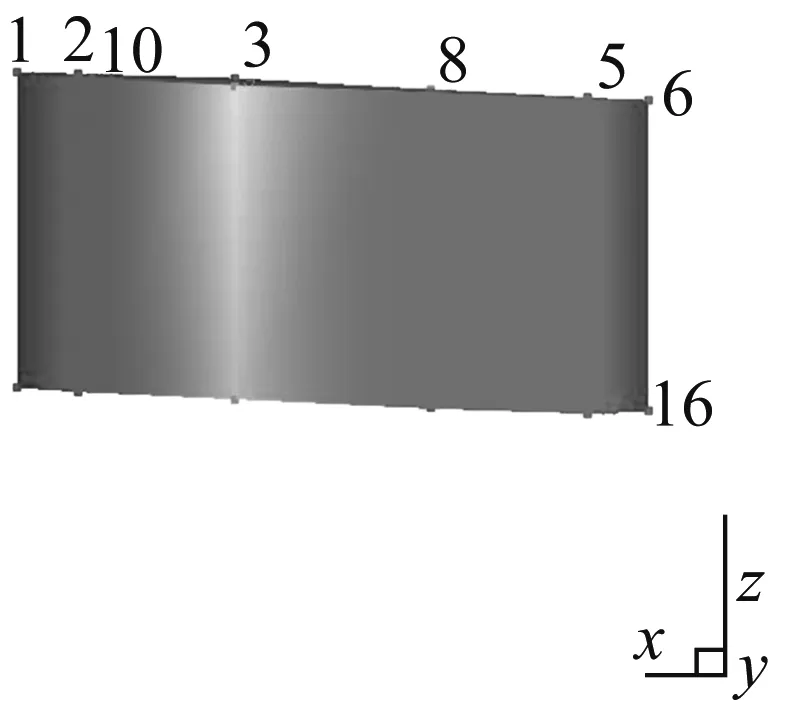
(e)

(f)

Fig.4 The axial vibration mode of dry gas seal under 1 MPa-4 000 r/min working condition

模態置信度(MAC)用于衡量不同模態振型的相關度，可利用不同階次模態進行MAC相關性分析驗證模態結果。1 MPa-4 000 r/min工況下軸向測試三階模態MAC分析結果振型獨立性在接受范圍內，如圖5所示。其中Cross Half PSD函數的效果(b)較Cross Power Spectra(a)獨立性更好。

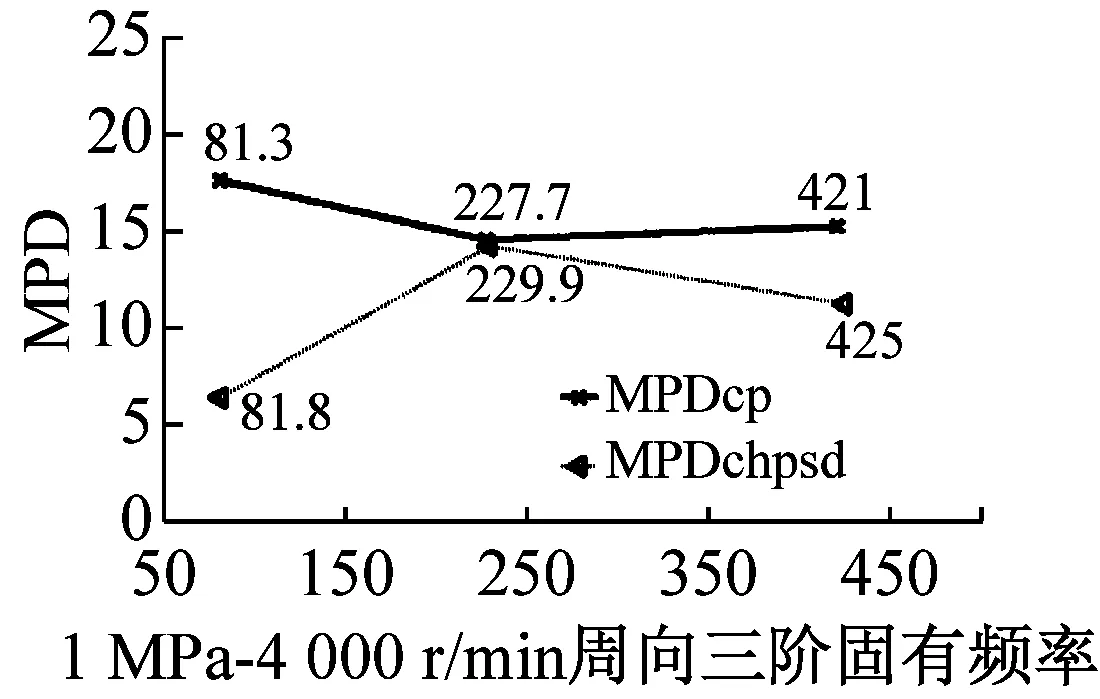
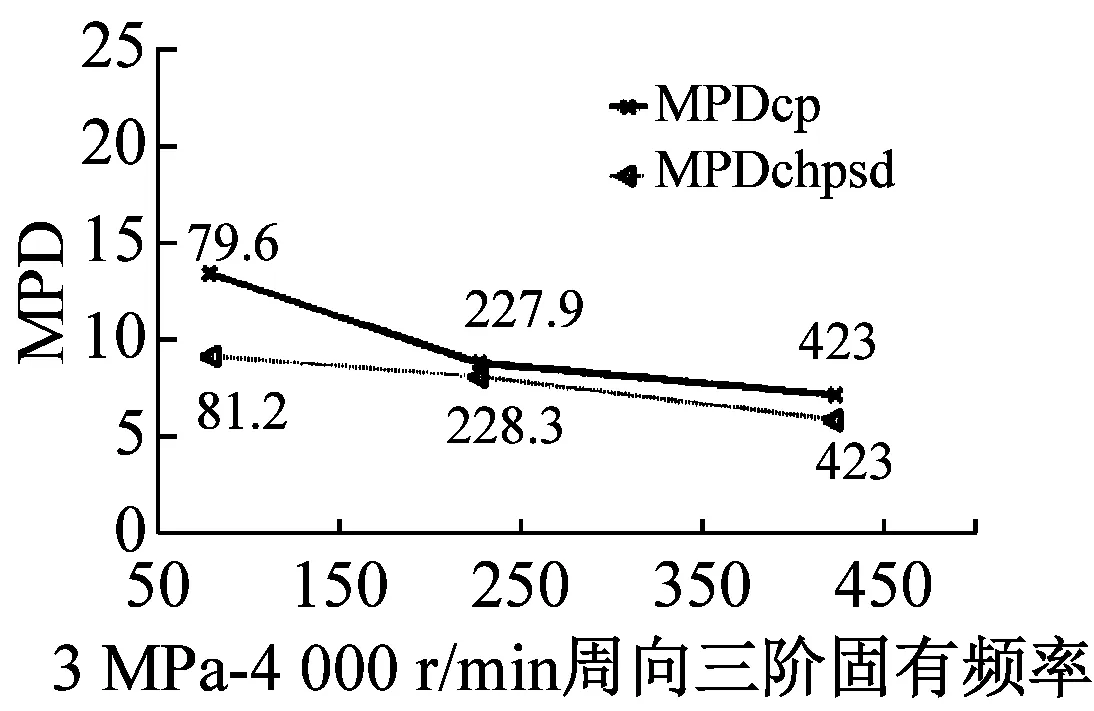
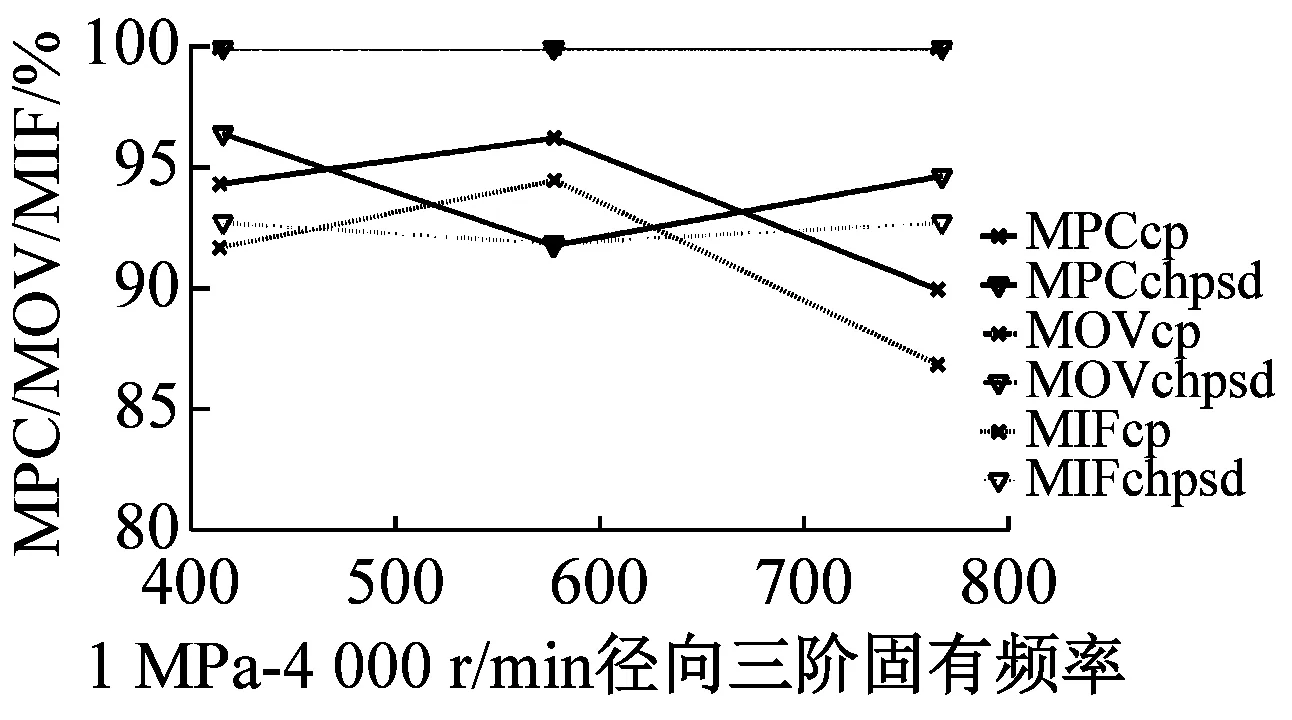
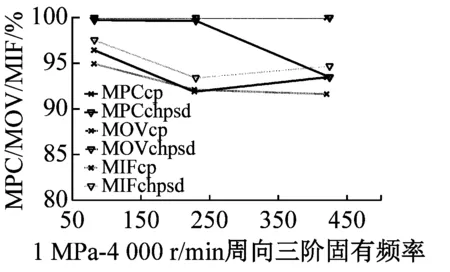
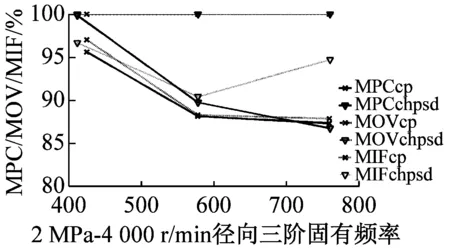
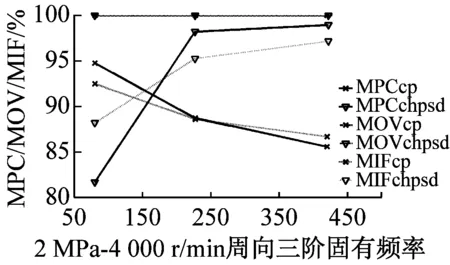
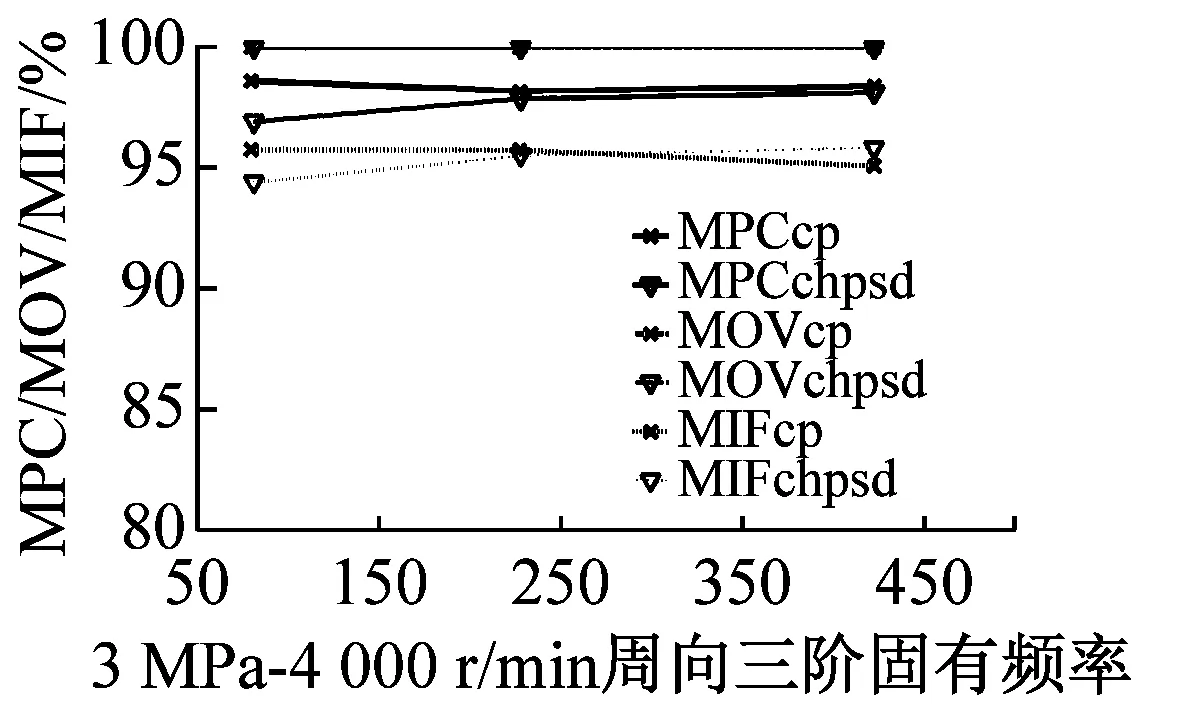
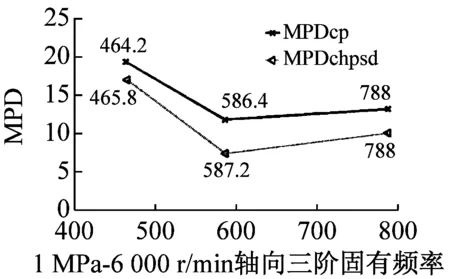
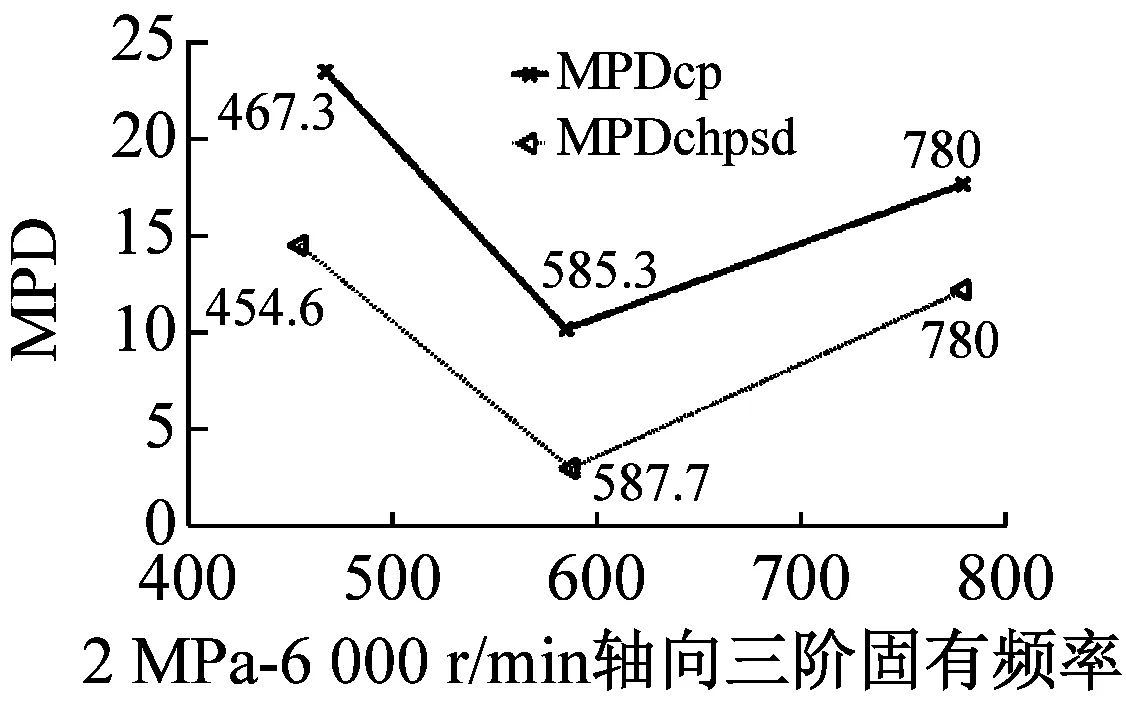
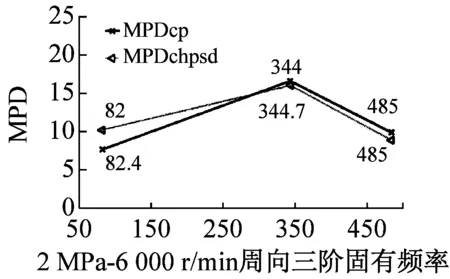
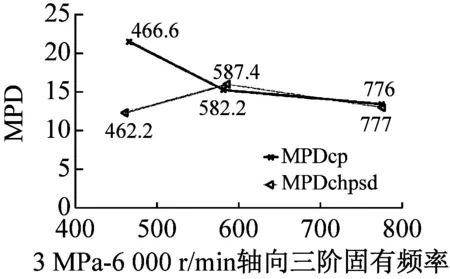
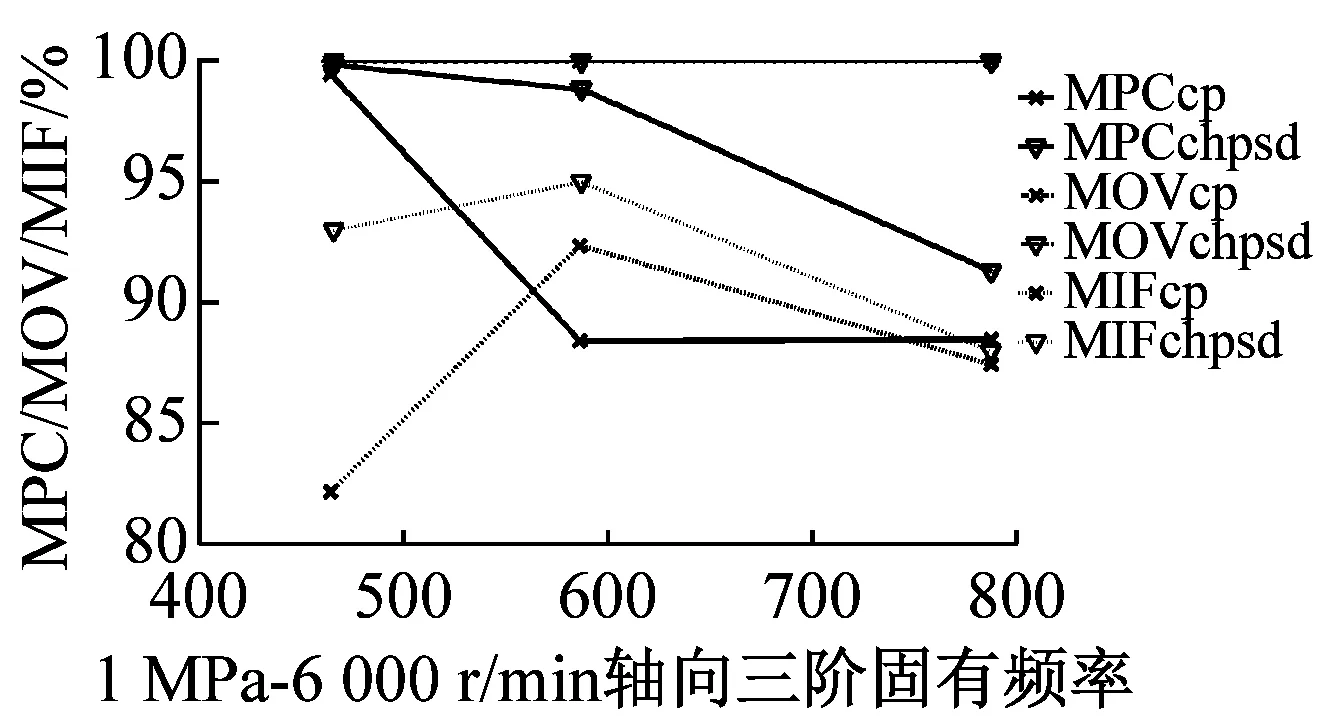
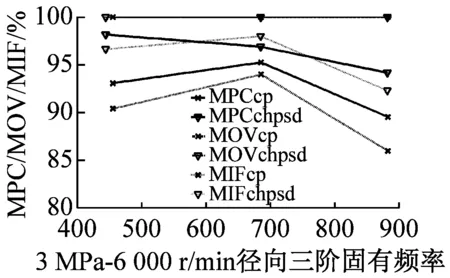
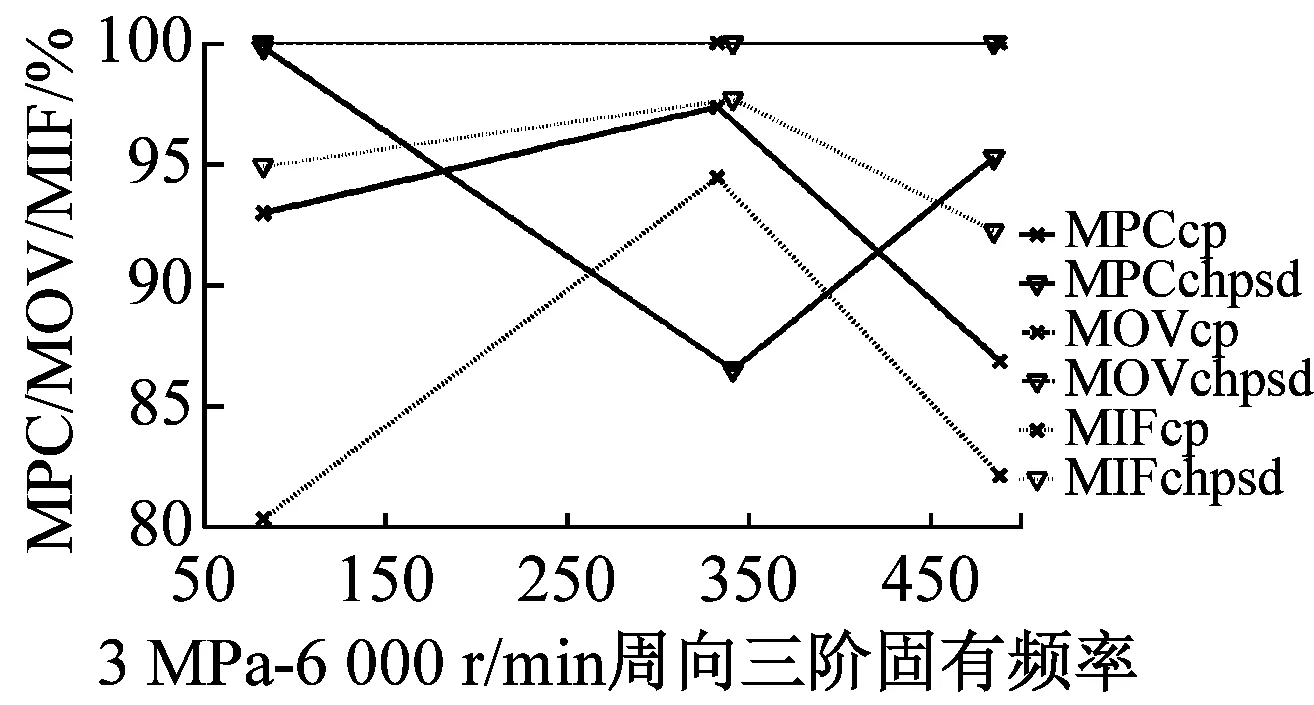
最后利用MPD、MPC、MOV以及MIF進行模態最終驗證，MPDc、MPCcp、MOVcp以及MIFcp為Cross Power Spectra函數結果，MPDchpsd、MPCchpsd、MOVchpsd以及MIFchpsd為Cross Half PSD函數結果，如圖6所示。其中，MPD值越小越好，而MPC、MOV和MIF越接近100%越好，MPD<20，MPC、MOV和MIF在80%以上的結果均為工程測試可接受結果。圖7為不同操作條件(轉速r與介質壓力p)下，干氣密封裝置系統模態參數f變化趨勢。

2.4 試驗結果

由圖6驗證結果可知，對于干氣密封裝置的模態分析，Cross Half PSD函數的分析效果更為可取。Cross Half PSD函數下90%以上的MPD值均小于Cross Power Spectra的MPD值，即模態相位的標準差更小，Cross Half PSD函數下的MPC和MIF相比于Cross Power Spectra更接近于100%，MOV值均為100%說明噪聲或算法產生的虛假模態得以剔除。

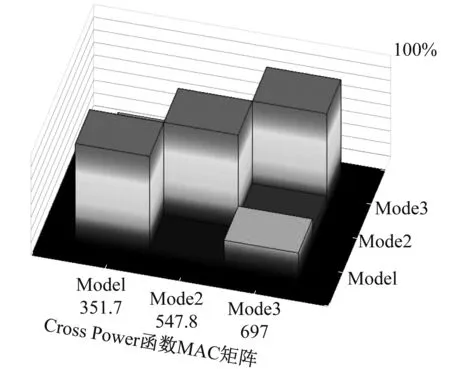
(a)

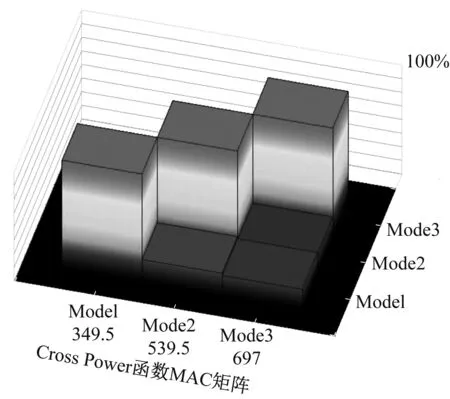
(b)

圖5 函數Cross Power Spectra與Cross Half PSD的固有頻率MAC矩陣

Fig.5 The natural frequency MAC matrix from the Cross Power Spectra function and Cross Half PSD function

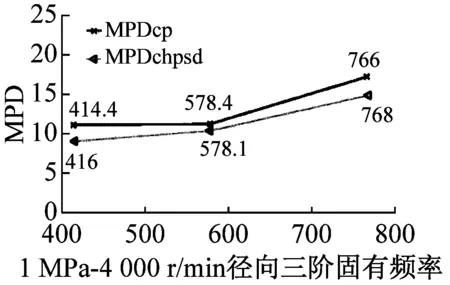
(a)

(b)

(c)

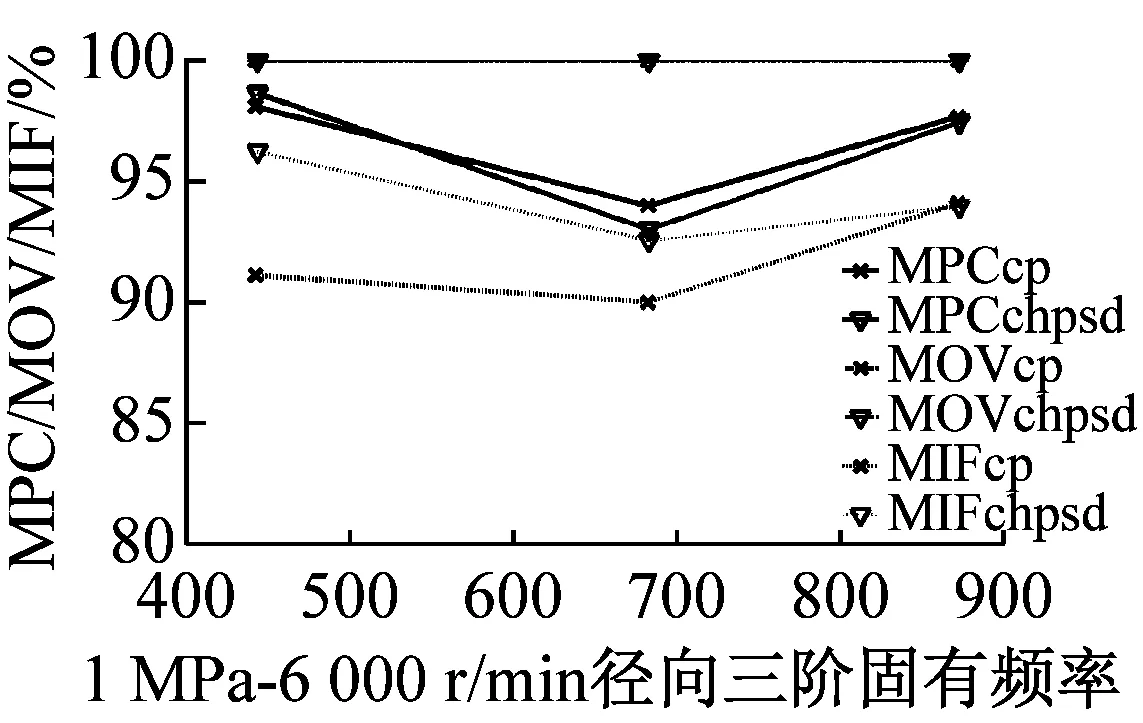
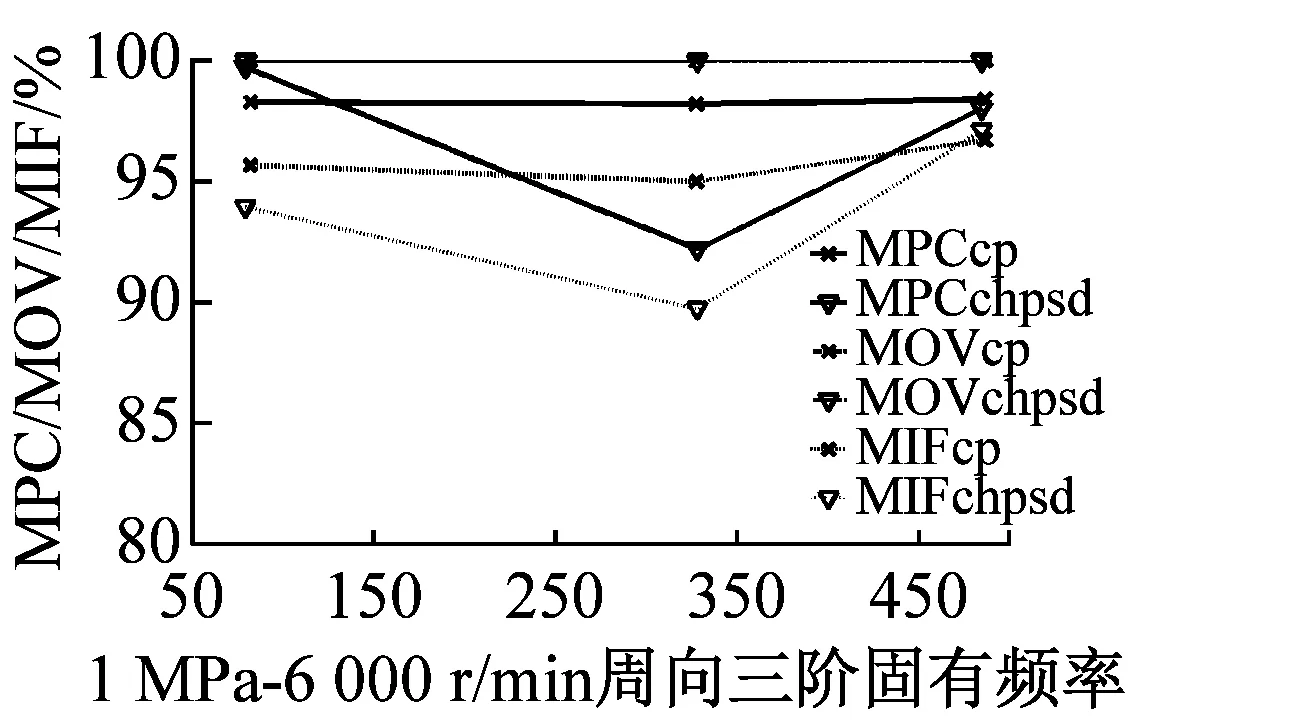
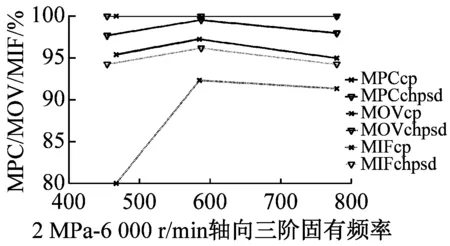
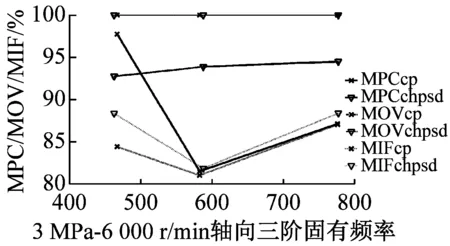
(d)

圖6 各階模態MPD、MPC、MOV以及MIF值

Fig.6 The MPD、MPC、MOV、and MIF for modes

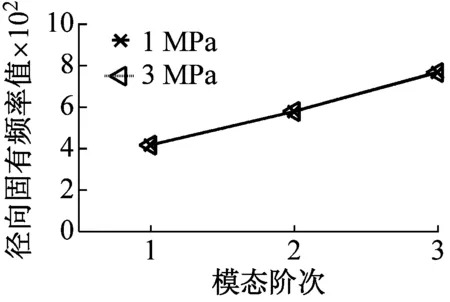
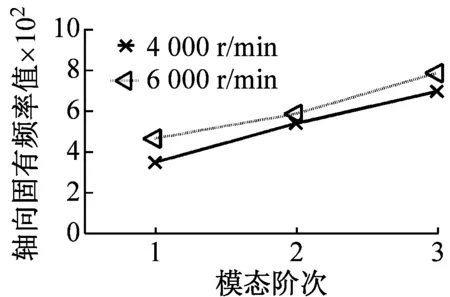
由圖7中模態參數f變化分析結果可知，隨著介質壓力的變化，軸向固有頻率略有變動，但此變動不大，是由實驗測試誤差引起；但當轉速增加時，軸向固有頻率值明顯增大，其中一階固頻增加幅度大于二階、三階固頻值，說明介質壓力對于干氣密封裝置的軸向模態參數并無較大影響，但是轉速對于系統軸向固頻影響較大，其中對于軸向一階模態參數影響較為明顯。同樣，介質壓力的改變對于干氣密封徑向模態參數影響也不大；但一階、二階、三階固有頻率隨著轉速的增加均有增大，其中二階、三階固頻值增幅大于一階固頻值，說明轉速對于密封徑向二階、三階模態影響較大。介質壓力的改變對于周向模態影響也很小；轉速對于周向一階模態也未見明顯影響，但是轉速的增加對周向二階、三階模態影響明顯，隨著轉速的增加，周向二階、三階固有頻率值增大。由上述結果總結：干氣密封的介質壓力和轉速這兩個重要操作條件中，介質壓力對于干氣密封系統模態特性影響較小，轉速條件對于系統模態參數影響較大，并且對于軸向、徑向和周向三個方向的模態特性影響各不相同，干氣密封在工作時，當轉速設計發生改變時，應注意軸向一階、徑向二階、三階以及周向二階、三階的模態變化，以防止發生嚴重失效。

(a)

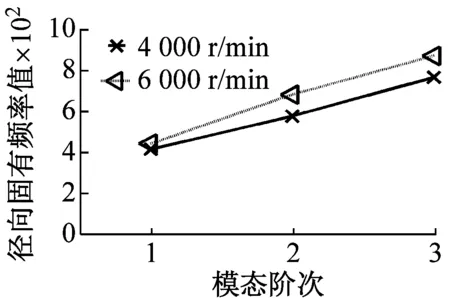
(b)

圖7 不同操作條件下系統三向固有頻率變化趨勢

Fig.7 The system natural frequencies change trend of three directions under different medium pressure and rotational speed

3 工作模態響應面模型建立

3.1 響應面模型

為實現不同條件下工作模態預測，建立完整的二次多項式響應面模型，對于s個變量，響應面模型為

(10)

式中：α0為常數項待定系數;αj為一次項待定系數;αij為二次項待定系數。

令

(11)

(12)

式中:Xv=(x1,x2,…,xs);xi(i=1,2,…,s)為設計變量;βk為未知系數;其個數k=(s+1)(s+2)/2;故β=(β0,β1,…,βk-1)T;利用最小二乘原理確定未知系數βk，獨立試驗次數t要不小于k，即t≥k[20]。

3.2 Box-Behnken試驗設計

Box-Behnken試驗設計是既能以最少試驗循環又能提供關于試驗變量的較完整信息的試驗設計，以不同的操作條件(介質壓力p與轉速r)、方向D和模態階數N為響應面變量，試驗設計結果如表4所示。

表4 Box-Behnken試驗設計表

3.3 回歸分析與預測

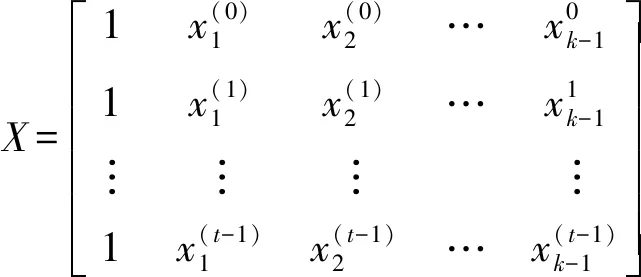
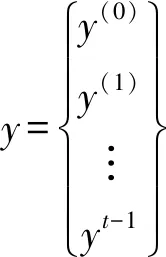
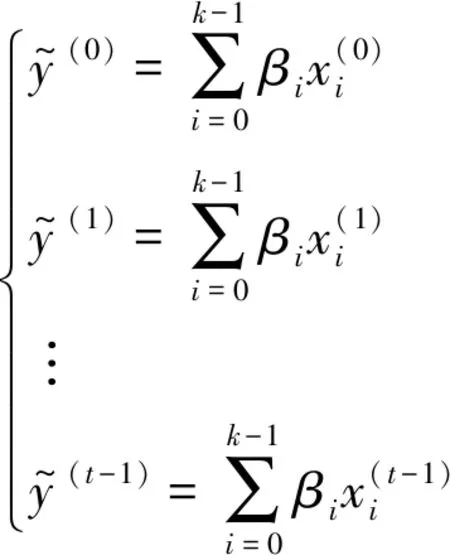
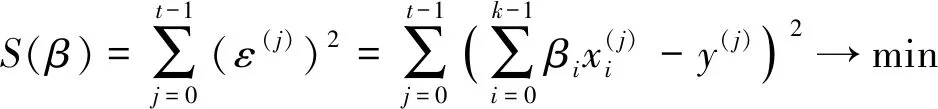
取極小值的必要條件

(l=0,…,k-1)

(13)

即(Xβ-y)TX=0

(14)

則β=(XTX)-1XTy

(15)

(16)

(17)

(18)

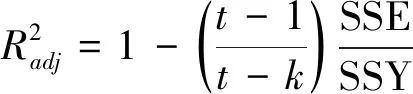
(19)

(20)

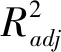
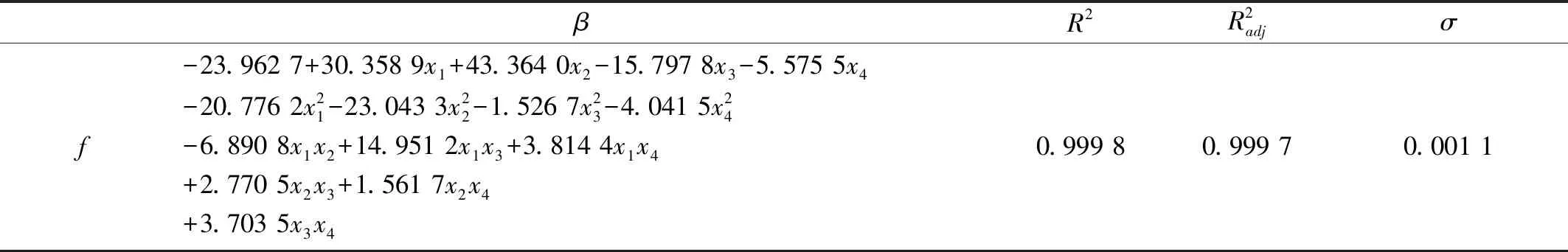
表5 完整二次響應面模型和評價指標

表6 預測結果

4 結 論

(1) 基于多參考點最小二乘復頻域法(PolyLSCF)，分別采用互功率譜函數(Cross Power Spectra)和半互功率譜密度函數(Cross Half PSD)實現對裝置系統的工況模態分析及識別；并通過數學指標：模態置信度(MAC)、平均相位偏差(MPD)、模態相位線性度(MPC)、模態復雜性(MOV)以及模態指示函數(MIF)進行模態驗證。

(2) 結果表明半互功率譜密度函數的分析結果好于互功率譜函數，因此半互功率譜密度函數更適用于復雜結構系統的工作模態分析。同時，干氣密封的介質壓力和轉速這兩個重要操作條件中，介質壓力對于干氣密封系統模態特性影響較小，轉速條件對于系統模態參數影響較大，并且對于軸向、徑向和周向三個方向的模態特性影響各不相同。然后基于響應面方法與模態分析結果，建立了一種時變模態參數識別的模型，以不同的操作條件(介質壓力與轉速)、方向和模態階數為響應面變量，通過Box-Behnken試驗設計選取合適的變量樣本點，建立系統模態參數的完整二次多項式工作模態響應面模型，實現了模態固有頻率預測，為時變模態的辨識提供了新的技術方案。