半監督多源域適應集成的球磨機負荷參數軟測量

李思思, 閻高偉, 閆 飛, 程 蘭, 杜永貴

(1.太原理工大學 電氣與動力工程學院，太原 030024;2.山西工程技術學院，陽泉 045000)

流程工業在實際運行過程中，由于運行任務與設定值的變化、外界環境的改變、設備重組等因素，會導致工況發生改變[1]。球磨機是應用于電力、化工等流程領域的典型設備，具有強耦合、非線性和多工況等特點。該設備負荷參數的準確檢測對于磨礦作業環節的質量控制、磨礦效率和能耗降低起著至關重要的作用。因此，本文以球磨機負荷參數的預測為例開展研究。

目前，球磨機負荷參數檢測受限于建模機理及物理條件的復雜性，常采用軟測量方法建模，即選擇與主導變量相關的輔助變量(筒體振動或振聲信號[2-3])建立軟測量模型得到負荷參數預測值。常見的建模方法有偏最小二乘(Partial Least Squares，PLS)[4]、核模糊回歸[5]以及極限學習機(Extreme Learning Machine，ELM)[6]等。上述建模方法僅適用于單一工況的數據。

在實際運行過程中，不定期添加鋼球或輸入礦石成分的變化會引起工況的改變。工況改變后導致待測數據(目標域數據)和歷史數據(源域數據)分布存在差異及待測工況數據不足的問題。若根據源域數據建立軟測量回歸模型，則會違背機器學習方法建立在數據同分布條件的前提；若利用少量目標域數據建模，模型預測效果往往不理想。近年來，為適應工況的變化，廣泛采用即時學習、集成學習的建模策略。文獻[7]提出一種基于k近鄰的局部建模方法。文獻[8]引入因果關系利用動態主成分分析實現過程監控。Ma等[9]和Jaffel等[10]運用移動窗策略，對模型實時更新。針對在線測量中可能產生的偏差，Shao等[11]提出半監督的選擇性集成建模策略。然而，即時學習在數據分布差異大的情況下會形成較大的期望風險，集成學習更新策略由于各子模型的輸出置信難以估計，存在較大的結構風險。

因此，針對工況改變引起的模型失配問題引入遷移學習[12-14]策略。該策略放寬了數據服從同分布的假設，通過抽取領域間“隱含語義”或挖掘領域間“共享知識結構”，利用源領域已有的知識來解決未知目標領域(但與源領域相關)中僅有少量有標簽樣本數據甚至沒有標簽樣本情況下的學習問題。遷移學習方法分為特征表示法和實例權重法。流形正則化域適應[15]通過特征映射實現知識的遷移。但是，流形正則化域適應是一種無監督的方法，在特征變換過程中不能有效利用已有的標簽信息，導致算法性能受到影響。為此，將標簽信息引入流形正則化域適應的目標函數，研究基于半監督域適應的球磨機負荷參數軟測量方法，該方法優點為：① 通過遷移學習的方法實現變工況數據的建模；② 將標簽信息考慮在特征空間變換的過程中以提高負荷參數預測精度。為進一步提高模型預測精度，采用多源域集成策略，利用多源域信息互補，更加有效地遷移源域知識到目標領域，提高目標領域的預測能力。

1 理論與算法

遷移學習是運用已有的知識對不同但相關領域問題進行求解的一種新的機器學習方法。該方法放寬了傳統機器學習中的兩個基本假設：① 用于學習的訓練樣本與新的測試樣本滿足獨立同分布的條件；② 必須有足夠可利用的標記樣本才能習得一個好的模型。本文通過流形正則化保持空間結構不變；通過最大方差保證目標域數據對不同負荷參數表示能力；通過希爾伯特-施密特獨立標準(Hilbert-Schmidt Independence Criterion，HSIC)[16]引入標簽信息；通過擴展非參數最大均值差異減小源域和目標域的均值距離，得到特征變換矩陣，將歷史數據和待測數據映射到公共子空間。具體方法如下。

1.1 流形正則化域適應方法

針對不同工況數據分布差異性的問題，采用流形正則化域適應的方法實現負荷參數預測。該方法首先集成流形約束、最大方差及擴展非參數最大均值差異方法得到最佳特征變換矩陣；然后，將目標域數據和源域數據的特征信息通過投影變換矩陣投影到公共子空間；最后，應用統計方法(如PLS)或神經網絡(如反向傳輸神經網絡(Back Propagation，BP))建立軟測量模型，從而合理、有效地對目標域球磨機負荷參數進行預測。其目標函數為

(1)

式中：V為特征變換矩陣;L為Laplacian矩陣;Mc為擴展非參數最大均值差異矩陣;上標s、t分別表示源域數據及目標域數據;X=[Xs,Xt];λ1、λ2為平衡因子。

1.2 半監督域適應方法

流形正則化域適應屬于無監督特征映射方法，無法將標簽信息融入特征映射的過程來提高公共子空間數據的可辨識屬性。為提高模型預測精度，將少量目標域及源域的標簽信息引入流形正則化域適應，解決數據分布差異造成模型預測精度低的問題以及待測工況樣本少的問題。

本文通過HSIC將標簽信息引入流形正則化域適應。HSIC計算兩組數據集間再生核希爾伯特空間的協方差來衡量數據之間的獨立性。設Kx、Ky為兩組數據集X、Y相應的核矩陣，由文獻[16]得希爾伯特經驗估計為

EHSIC=(n-1)-2Tr(KxHKyH)

(2)

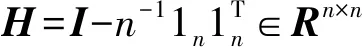
max Tr(VTXHYHXTV)

(3)

將式(3)引入式(1)得到半監督域適應的目標函數

(4)

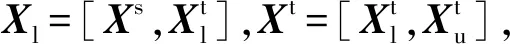
為求得特征變換矩陣V，將式(4)最大化問題轉化為

(5)

引入拉格朗日乘子

(6)

式(6)對V求偏導，并令其為0，得：

τV=(λ3XsLs(Xs)T+

(7)

半監督域適應方法具體過程如表1所示。

表1 半監督域適應方法

半監督域適應方法利用源域數據、目標域數據、源域數據標簽及少量目標域數據的標簽信息得到特征變換矩陣；然后，將源域數據及目標域數據投影到公共子空間。該過程充分考慮標簽信息對特征變換矩陣的作用、數據流形結構的不變性，從而提高球磨機負荷參數的預測精度。

1.3 半監督多源域適應方法

半監督域適應是遷移已有單一源域的知識來解決未知目標領域的域適應學習方法。當歷史數據庫中有多個源域時，如果僅使用其中一個域作為源域進行訓練就會忽略其它域對目標域的有用信息，且不同源域數據存在信息相關與互補的特點，因此，可以充分利用多個源域的數據從而提高模型的預測性能。本文建立基于半監督多源域適應集成的軟測量模型。該模型首先根據式(8)求得特征變換矩陣V′；然后分別將多個源域及目標域數據投影到公共子空間，并建立相應的回歸模型；最后通過最大均值差異(Maximum Mean Discrepancy, MMD)加權多個源域負荷參數預測值。

(8)

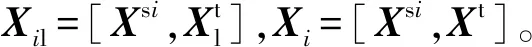
(9)

半監督多源域適應方法具體過程如表2所示。

表2 半監督多源域適應方法

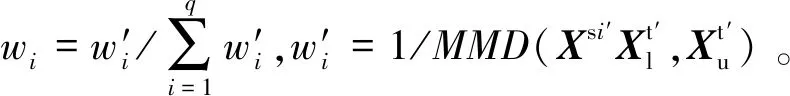
2 實驗研究

球磨機負荷參數(如料球比(Material to Ball Volume Ratio，MBVR)、濃度(Pulp Density，PD)、充填率(Charge Volume Ratio，CVR))的準確檢測對于磨礦作業環節的質量控制、磨礦效率和能耗降低起著至關重要的作用[17]。為此，采集與負荷參數相關的振動信號，建立模型，得到負荷參數預測值。

2.1 數據采集與預處理

實驗采用Φ602 mm×715 mm小型實驗球磨機。其中，球磨機最大鋼球裝載量為0.6 t，實驗過程筒體轉速為43 r/min。磨機筒體中部有圓形加料口，用于添加鋼球、物料和水。實驗過程采用的物料是鐵礦粉，密度為2.3 t/m3。研磨介質采用直徑為30 mm的鋼球。球磨機型號為Y112M-4的三相異步電機驅動。三相電機功率為4 kW、額定電流為8.8 A、電壓380 V、轉速為1 440 r/min。

首先，在軸承座上安裝振動傳感器，通過振動傳感器采集振動信號；然后利用數據采集模塊將振動傳感器輸出的模擬信號放大并轉換成數字信號，送入上位機，用LabVIEW編寫的程序完成數據的讀取、顯示和保存工作。

通過改變介質充填率(Ball Charge Volume Ratio，BCVR)來模擬工況突變，即分別采集BCVR為0.30、0.35、0.40、0.45、0.50的5組實驗數據。這5組數據對應工況為工況1、工況2、工況3、工況4、工況5。每組實驗通過連續添加物料量改變CVR、MBVR、PD。每個工況下的數據如表3所示。以工況1的數據為例，分別固定球磨機筒體內球和水的質量，筒體內物料由起始重量25.5 kg逐漸增加到174 kg，共增加了139次。

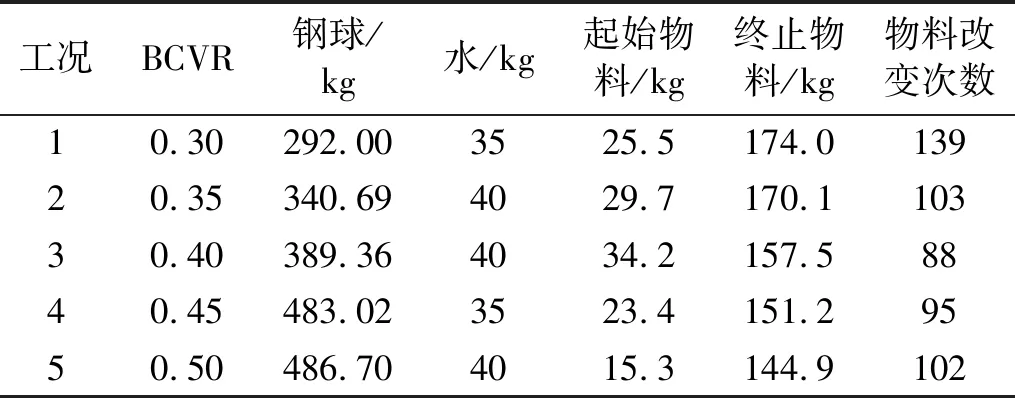
表3 工況突變實驗情況

將每個工況振動信號平均分為28個樣本，每個樣本覆蓋長度大于濕式球磨機旋轉一周所用時間，然后將時域信號通過快速傅里葉變換轉換為頻域信號。

鄰域保持嵌入(Neighborhood Preserving Embedding，NPE)[18]算法通過最優映射變換矩陣將數據從高維空間映射到低維的特征空間中。在低維空間中保持數據固有的局部領域流形結構不變性。以介質充填率變化的五種工況為例，每個工況下隨機選取500個振動信號的樣本，通過NPE將高維頻譜特征降維至三維空間進行可視化。圖1給出了五種工況下數據三維空間的分布情況。從圖1可知,在不同工況下，數據分布存在差異性。

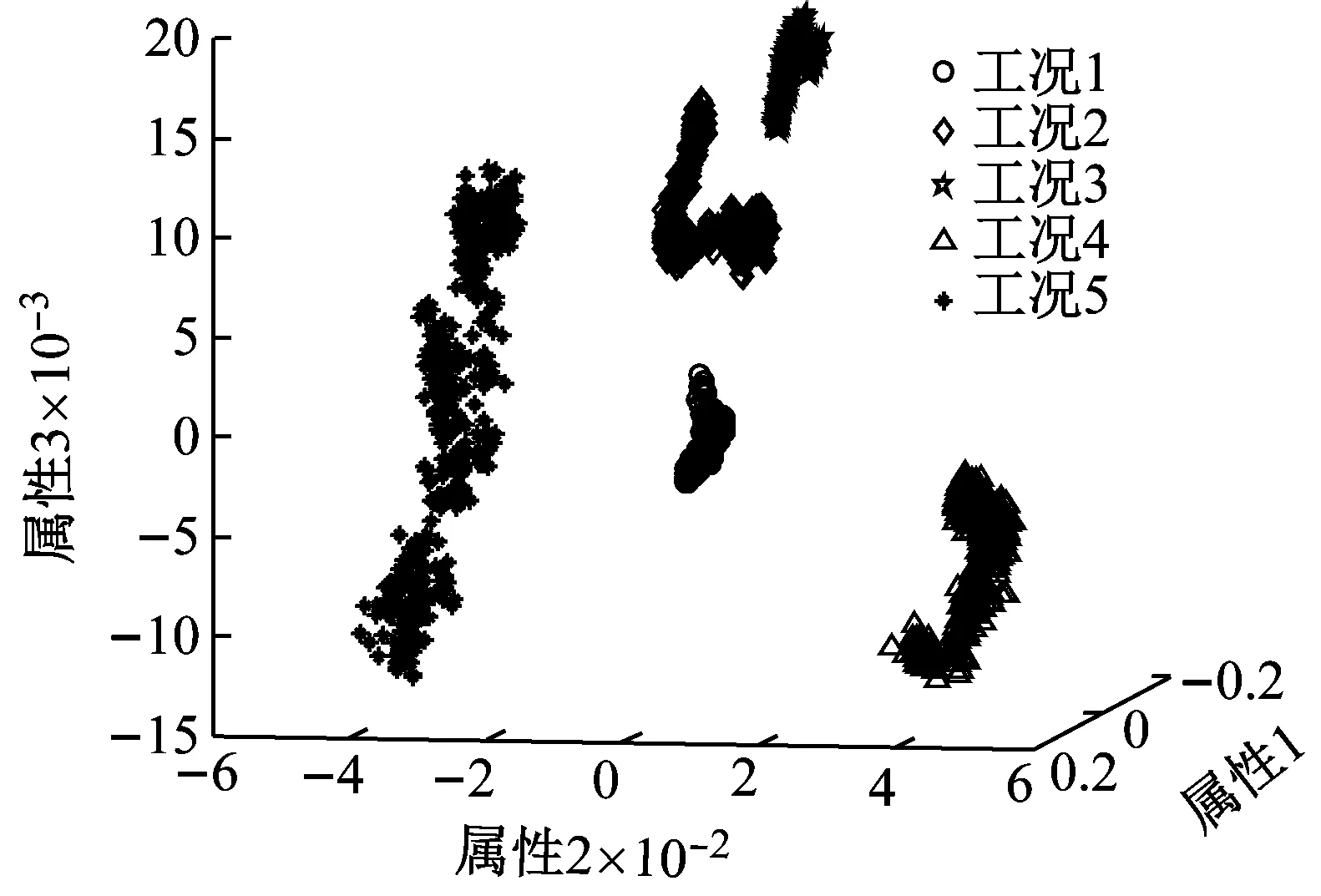
圖1 不同工況數據降維后的分布情況

Fig.1 The distribution of data of different working conditions after dimensionality reduction

2.2 基于半監督域適應的磨機建模方法

基于半監督域適應球磨機負荷參數建模方法通過特征映射將數據從高維空間投影到公共子空間，實現負荷參數較高精度預測。

2.2.1 特征映射

特征映射具體過程如下：根據表1的Step1～Step3將源域數據、目標域有標簽數據、目標域無標簽數據分別投影到公共子空間。其中式(7)中參數λ3、λ4和λ5通過網格搜索法確定。

為得到特征變換后的數據分布情況，采用半監督域適應將源域和目標域數據進行特征映射，并與傳統降維方法(NPE)作對比。首先，利用工況1的數據作為源域數據，工況3的數據作為目標域數據。然后，分別通過NPE、半監督域適應得到特征變換后的數據。最后，以特征變換后的第一維數據為例繪制圖2。圖2中:NPE_S、NPE_T、SDA_S、SDA_T分別為NPE降維后源域數據、目標域數據、半監督域適應變換后的源域數據、目標域數據。由圖2可知，半監督域適應方法可以有效減小特征變換后源域和目標域數據中心差異。

圖2 數據分布圖

2.2.2 負荷參數預測

為驗證本文方法的有效性，設計兩組對比試驗。第一組在工況變化后，利用少量目標域數據建模得到負荷參數預測值。第二組借助源域數據建模得到負荷參數預測值。為了評價各種模型的預測能力，本文使用均方根誤差(Root Mean Square Error，RMSE)作為度量準則。

在第一組實驗中，隨機選取目標域數據中的20個樣本作為少量帶標簽樣本。利用偏最小二乘回歸(Partial Least Squares Regression，PLSR)建立軟測量回歸模型得到負荷參數預測值。參數預測情況如圖3及表4所示。圖3中傳統方法指利用工況3中隨機抽取的20個樣本建立偏最小二乘回歸模型得到負荷參數預測值。表4中，“少量3”表示利用傳統方法建模得到負荷參數預測的RMSE。由圖3可知，根據少量待測工況樣本建立的模型無法預測負荷參數值。因此有必要借助歷史工況數據建模。

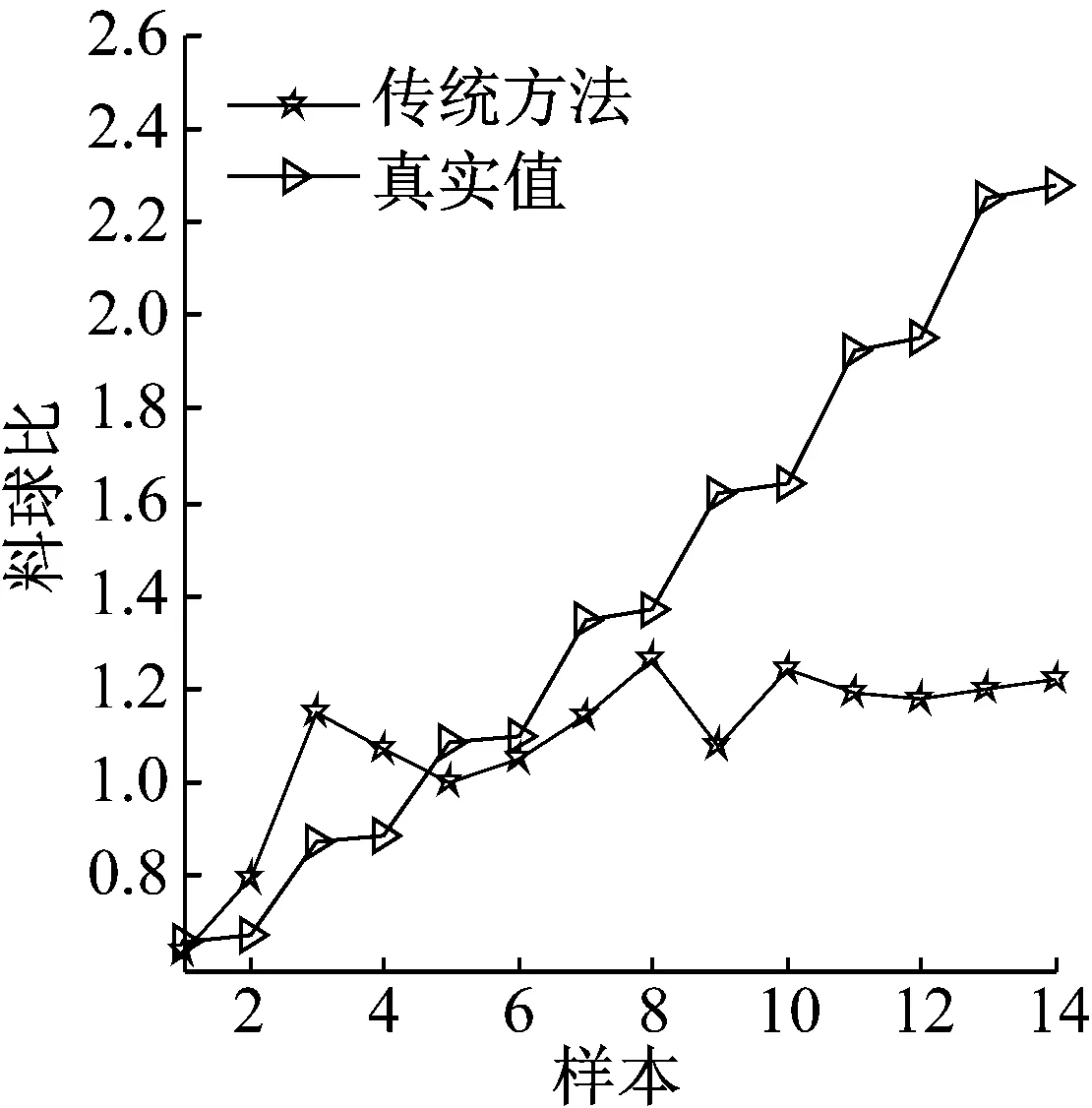
圖3 少量樣本建模負荷參數預測結果

Fig.3 Load parameter prediction results of a small amount samples

第二組實驗借助源域數據建模。為模擬實際工業過程中目標域存在少量帶標簽樣本的現象，隨機選取目標域數據中的20個樣本作為少量帶標簽樣本。半監督域適應方法根據“2.2.1”節中投影到公共子空間的源域數據和目標域少量帶標簽數據，建立PLSR模型從而得到目標域中無標簽樣本的負荷參數預測結果。近年來，為使系統模型能夠及時適應工況的變化，即時學習和集成學習的建模策略被廣泛采用。因此，本文采用傳統方法、即時學習、集成學習及“1.1”節中的流形正則化域適應方法作為對比實驗。傳統方法利用PLSR建立軟測量回歸模型；即時學習通過在歷史數據庫中尋找與目標域數據相似的樣本，然后根據相似樣本建立PLSR回歸模型；集成學習使用各個學習器間不存在依賴關系的隨機森林建立模型。對比結果如圖4及表4所示。

圖4 工況2→工況3負荷參數預測結果

Fig.4 Load parameters prediction results of working condition 2 transfer to working condition 3

表4 單源域負荷參數預測均方根誤差對比

Tab.4 Comparison of RMSE in single source domain load parameter prediction

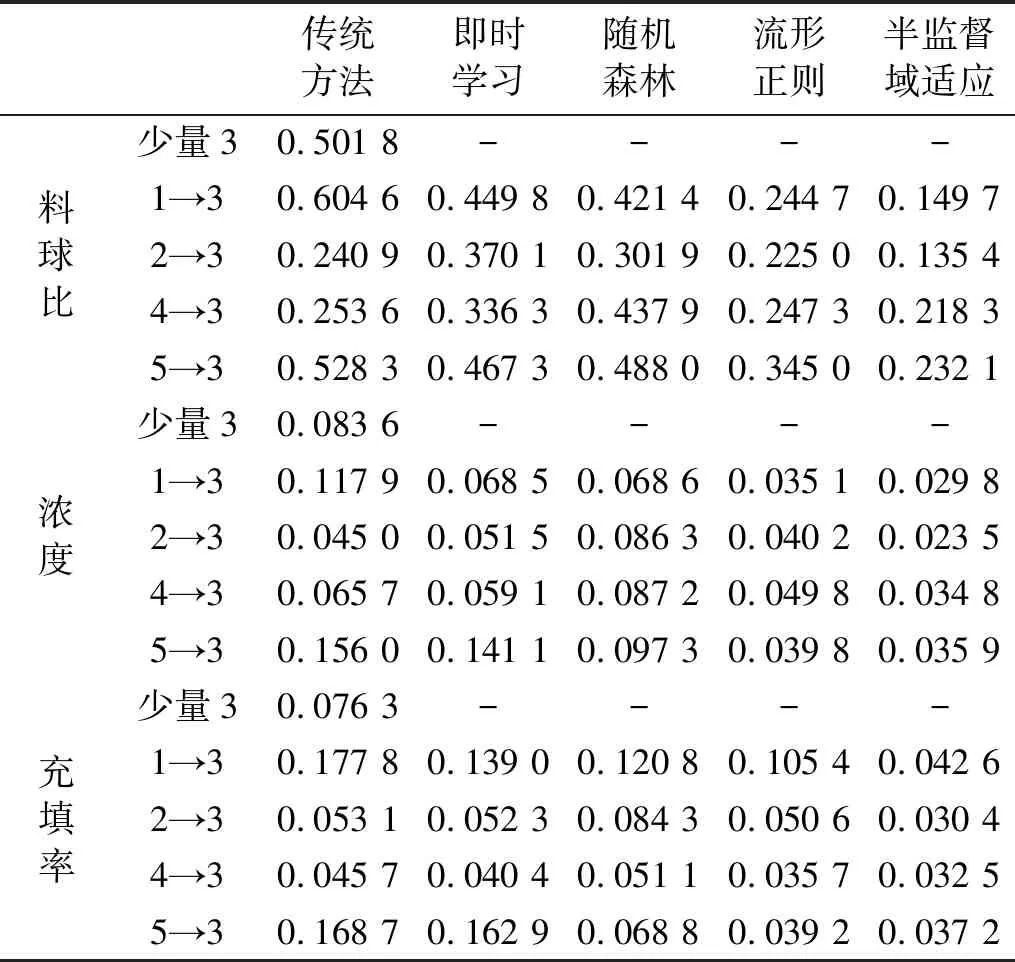
傳統方法即時學習隨機森林流形正則半監督域適應料球比少量30.501 8----1→30.604 60.449 80.421 40.244 70.149 72→30.240 90.370 10.301 90.225 00.135 44→30.253 60.336 30.437 90.247 30.218 35→30.528 30.467 30.488 00.345 00.232 1濃度少量30.083 6----1→30.117 90.068 50.068 60.035 10.029 82→30.045 00.051 50.086 30.040 20.023 54→30.065 70.059 10.087 20.049 80.034 85→30.156 00.141 10.097 30.039 80.035 9充填率少量30.076 3----1→30.177 80.139 00.120 80.105 40.042 62→30.053 10.052 30.084 30.050 60.030 44→30.045 70.040 40.051 10.035 70.032 55→30.168 70.162 90.068 80.039 20.037 2

表4中“1→3”為工況1的數據作為源域數據工況3的數據作為目標域數據。由圖4及表4可知：①當數據分布差異大時，傳統方法、即時學習、集成學習結果相對較差。其原因為即時學習存在期望風險，集成學習存在結構風險，傳統方法建立在數據同分布的前提下;②在料球比、濃度、充填率參數預測中，流形正則化域適應、半監督域適應都能以一定的精度實現負荷參數的預測，但是半監督域適應精度相對較高，其原因為考慮了標簽對投影矩陣的影響。

2.3 基于半監督多源域適應的磨機建模方法

在工業過程中，不同工況信息存在互補的特點，因此，可將多個源域的數據作為歷史數據建模得到負荷參數預測值。采用流形正則化多源域適應方法作為對比實驗。流形正則化多源域適應方法通過加權策略融合多個源域的數據。半監督多源域適應和流形正則化多源域適應方法建模后得到負荷參數預測均方根誤差結果,如表5所示。表中“1&2→3”為工況1、工況2的數據作為源域數據，工況3數據作為目標域數據。為直觀了解負荷參數預測情況，則以工況1和工況2為源域數據、工況3數據為目標數據為例，得到目標域料球比預測曲線，如圖5所示。由表5可知，半監督多源域適應方法比流形正則化多源域適應方法的預測均方根誤差小，精度高。對比表4及表5中工況3的預測均方根誤差得出，當充分利用多源域數據作為歷史數據時，半監督多源域適應方法可以挖掘出更多與負荷參數相關的特征信息，從而得到較高預測精度。

表5 多源域負荷參數預測均方根誤差對比

Tab.5 Comparison of RMSE in multi source domain load parameter prediction

1&2→34&5→3料球比流形正則化多源域適應0.224 10.255 4半監督多源域適應0.128 40.189 8濃度流形正則化多源域適應0.027 30.035 0半監督多源域適應0.022 40.021 4充填率流形正則化多源域適應0.043 50.032 2半監督多源域適應0.025 60.027 2

圖5 工況1 &工況2→工況3料球比預測結果

Fig.5 The MBVR prediction results of working condition 1 and working condition 2 transfer to working condition 3

3 結 論

本文針對球磨機工況改變后，歷史數據與待測數據分布差異導致的模型失配問題以及待測工況樣本少的問題，研究了半監督域適應方法及半監督多源域適應方法，得出如下結論：

(1) 域適應方法能夠有效改善數據概率分布失配對軟測量建模的影響，半監督域適應方法將標簽信息融入特征映射的過程能提高模型預測能力。

(2) 半監督多源域適應方法利用多源域信息互補的特點，更加有效地遷移不同源域知識到目標領域，提高目標領域的預測能力。

(3) 利用多工況下小型試驗球磨機數據進行實驗，結果表明：本文方法在一定程度上能有效跟蹤實際值的變化。這對選礦過程全流程優化運行和控制具有十分重要的意義。