步行荷載的兩階段遺傳算法識別

王鵬程， 陳 雋，2， 王浩祺

(1.同濟大學 土木工程學院，上海 200092； 2.土木工程防災國家重點實驗室，上海 200092； 3.東京大學 橋梁與結構實驗室，東京 113-8656)

隨著結構工程的發展，高強度輕質材料在新建建筑中得到了廣泛的使用，這使得越來越多的大跨樓蓋、人行橋、體育看臺等低頻、輕質、小阻尼結構出現了明顯的人致結構振動問題：人致激勵引起的結構的振動過大會引起結構上人群的不適甚至恐慌，嚴重時甚至會影響工程結構的安全性[1]。

可靠的步行荷載模型是人致結構振動分析的前提。自20世紀70年代以來，很多學者通過固定測力板、測力鞋墊以及動作捕捉等實驗方法，實測行人的步行荷載時程，提出了許多步行荷載的數學模型。Galbraith等[2]利用測力板數據，指出荷載曲線具有腳跟著地和腳尖離地的雙峰值特性；Ellingwood等[3]采用行走過程中左右腳落足曲線相同的假設，構造出單人步行荷載傅里葉時程曲線；Bachmann等[4]由實測數據得出了步行荷載的豎向前5階動載因子。Zivanovic等[5]在大量單人步行荷載實測數據的基礎上，把步頻、步長、荷載幅值視作正態分布，綜合主諧波及次諧波的峰值左右附近一定寬度的頻譜信息，擬合得出每階主諧波及次諧波的名義幅值表達式，建立了步行荷載的隨機模型;陳雋等[6]將三維動作捕捉技術與測力板相結合，將單步荷載實測值拓展為連續步行荷載，進而建立步行荷載的數學模型。

上述研究成果加強了人們對步行荷載特性的理解，并廣泛用于步行荷載下工程結構的振動分析。然而，隨著研究和應用的深入，基于剛性地面上實測數據的傳統荷載建模的方式也表現出一些問題：受實驗空間、測試者對測力板的“對準心理”、設備性能的限制等，無法全面反映測試者的真實步態；對于存在人結相互作用(Human-Structure-Interaction, HSI)的場合,剛性地面所得的荷載模型與實際荷載差異如何等。荷載建模的最終目的是準確計算結構響應。因此，針對上述問題并受車輛移動荷載識別方法的啟發，在前期由結構響應反演步行荷載時程的探索研究基礎上[7]，本文研究利用遺傳算法由結構響應識別步行荷載模型參數，并分別利用步行荷載的數學模型和實測記錄分別對方法的準確性及適用性進行了檢驗。

1 步行荷載的識別方法

1.1 單人步行荷載模型

步行荷載是人致結構振動問題中最重要的荷載形式。步行荷載是空間移動的連續性接觸荷載，可引起人行橋等長線性結構的豎向和水平振動。考慮左右腳荷載一致的情況，即步行過程可以看作成以一單步為基礎的周期性過程，則豎向的連續步行荷載可以表達為傅里葉級數的形式[8]

(1)

式中:Fv(t)為豎向力；G為人的靜止重力；αvi為豎向第i階傅里葉系數，又稱動載因子(Dynamic Loading Factor,DLF)；fp為行人的步行頻率；φvi為豎向第i階諧波相位角；n為模型階數。

模型階數的選擇應平衡荷載時程的準確表達以及未知參數的個數。參考已有研究成果，階數取為n=5。

除了作用力外，步行頻率也是步行荷載的一個重要指標。步行頻率即單位時間內的單步數，例如1.5 Hz表示1分鐘內走90步，步行荷載的頻率范圍大致在1.0～2.5 Hz[9]。

1.2 步行荷載下的結構響應

以一跨度為L的簡支梁為例，考慮其多階振型的影響，用廣義單自由度體系方法計算步行荷載作用下的結構位移響應。其簡化模型如圖1所示。

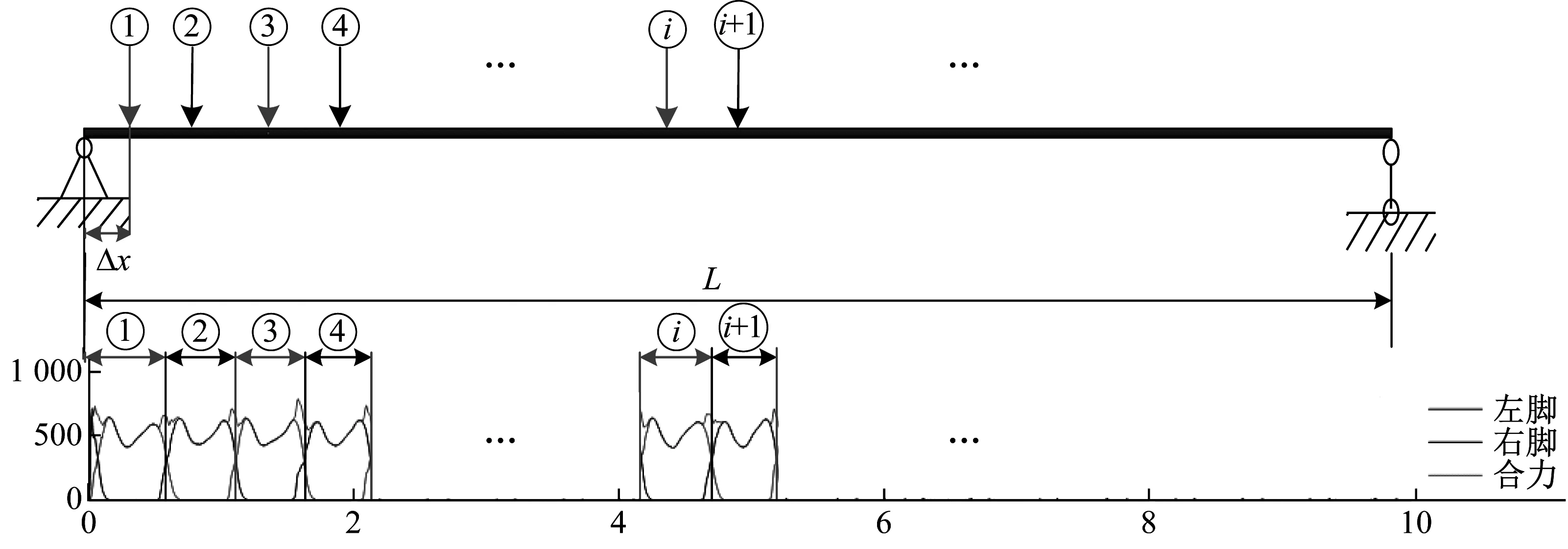
圖1 步行荷載作用在簡支梁橋上的簡化模型

簡支梁第i階振型的廣義動力學方程為

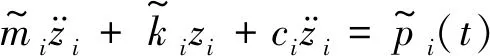
(2)

假設其第i階振型函數為

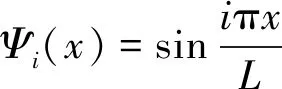
(3)

考慮左右腳位移的影響，確定步行荷載產生的廣義力為

(4)

A(t)=(nt+1)×v/fp+Δx

(5)

式中:Fv(t)為豎向的連續步行荷載時程曲線，nt為t時間內最大的單步數，nt=[t×fp]；v為步行速度；Δx為起步點至橋支座的水平距離。

在跨中x=L/2處，其總撓度為[10]

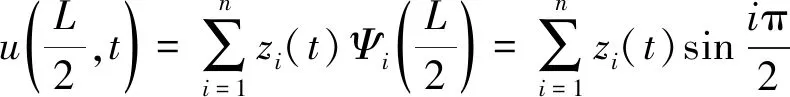
(6)

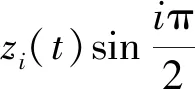
已有研究和工程經驗表明，振型越高，對結構響應貢獻越小。而疊加的參振振型過多，會影響計算效率。為簡化計算，本文所計算的結構響應是結構前4階跨中位移響應的疊加。

1.3 荷載參數的遺傳算法識別

需識別的荷載參數包括傅里葉級數的前五階動載因子及其相位、步行頻率fp等11個參數，行人的步行速度v和結構的位移反應時程u作為已知量。識別分為兩個階段進行：第一階段確定動載因子和步行頻率；第二階段確定相位。每階段的識別均采用遺傳算法實現。

遺傳算法(GA)是一類借鑒生物進化過程的全局優化搜索算法，模擬了自然選擇和遺傳中發生繁殖、交配和突變現象，從任一初始種群出發，通過隨機選擇、交叉和變異操作，最終生成符合優化目標的新個體。因其簡單通用、魯棒性強、適于并行計算及應用范圍廣等特點，廣泛用于各類識別問題。

根據以上特點，參考相關GA算例的運算流程[11]，步行荷載識別的具體實現過程可分解為如下六個步驟：

步驟1 編碼：即將11個參數轉換為二進制形式。假設每個參數二進制位數為20，將參數轉化后的二進制數依次排列。兩階段分別形成20×6=120、20×5=100個字符長度的字符串，對應的參數取值范圍如表1所示。

表1 待識別參數的取值范圍

步驟2 初始種群的生成：隨機產生一定數目的個體產生種群，即生成一定數目的字符串(參數組合)。本文中，種群大小皆設置為200。

步驟3 適應度評估：適應度表明個體的優劣性。不同的問題有著不同的適應性函數定義。適應度函數的大小與目標函數有關。兩個階段的目標函數分別為式(7)和式(8)所示。由于目標函數取最小值為最優解，故在本文中適應度函數為目標函數的倒數。

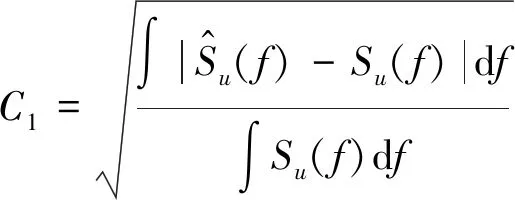
(7)

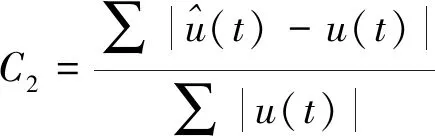
(8)

步驟4 選擇：選擇的目的是把優化的個體直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。常用的選擇方法有輪盤賭選擇法和隨機遍歷抽樣法，本文采用隨機遍歷抽樣法。

步驟5 交叉：交叉操作是遺傳算法中最主要的遺傳操作。通過交叉，遺傳算法的搜索能力得以飛躍提高。本文采用單點交叉法，交叉概率為90%。

步驟6 變異：變異的基本內容是群體中的個體串的某些基因值的依概率隨機變動。通常發生變異的概率很低,取值很小，本文為1%。

地桃花(Urena lobata L.)為錦葵科(Malvaceae)梵天花屬(Urena L.)植物[10]，是一種多年生亞灌木狀的直立草本，具有祛風利濕、活血消腫、清熱解毒的功效。我國長江以南地區均有地桃花分布。目前，對其化學成分分析和藥用價值等研究較多[11-14]。在野外調查中發現，地桃花和紫莖澤蘭可以共生，并表現出一定的競爭優勢，但地桃花提取物除草活性方面的研究鮮見報道。為全面了解地桃花提取物的除草活性，本研究在室內測定了地桃花提取物對10種植物幼苗生長的抑制作用，為這一植物源除草劑資源的開發利用提供依據。

算法采用謝菲爾德大學開發的GA工具箱實現[12]，以上步驟皆可通過工具箱的內置函數來調整參數，其參數配置匯總到表2中。

表2 遺傳算法參數配置

2 步行荷載模型的參數識別

2.1 結構模型的基本信息

考慮如圖2所示簡支梁橋，梁橋的長度L=20 m，線密度為ρ=60 kg/m，EI=3.6×107N·m2，前4階阻尼比均為ζ=0.02，前4階基頻分別為3.04 Hz、12.17 Hz、27.38 Hz和48.67 Hz。假設單人在該梁上行走，行人的體重為700 N,行走步距為0.75 m，步行頻率為2.0 Hz,步行速度為1.25 m/s。假定行走的第一步踩在距左端支座的0.5 m處。橋響應的測量點為跨中0.5L處。

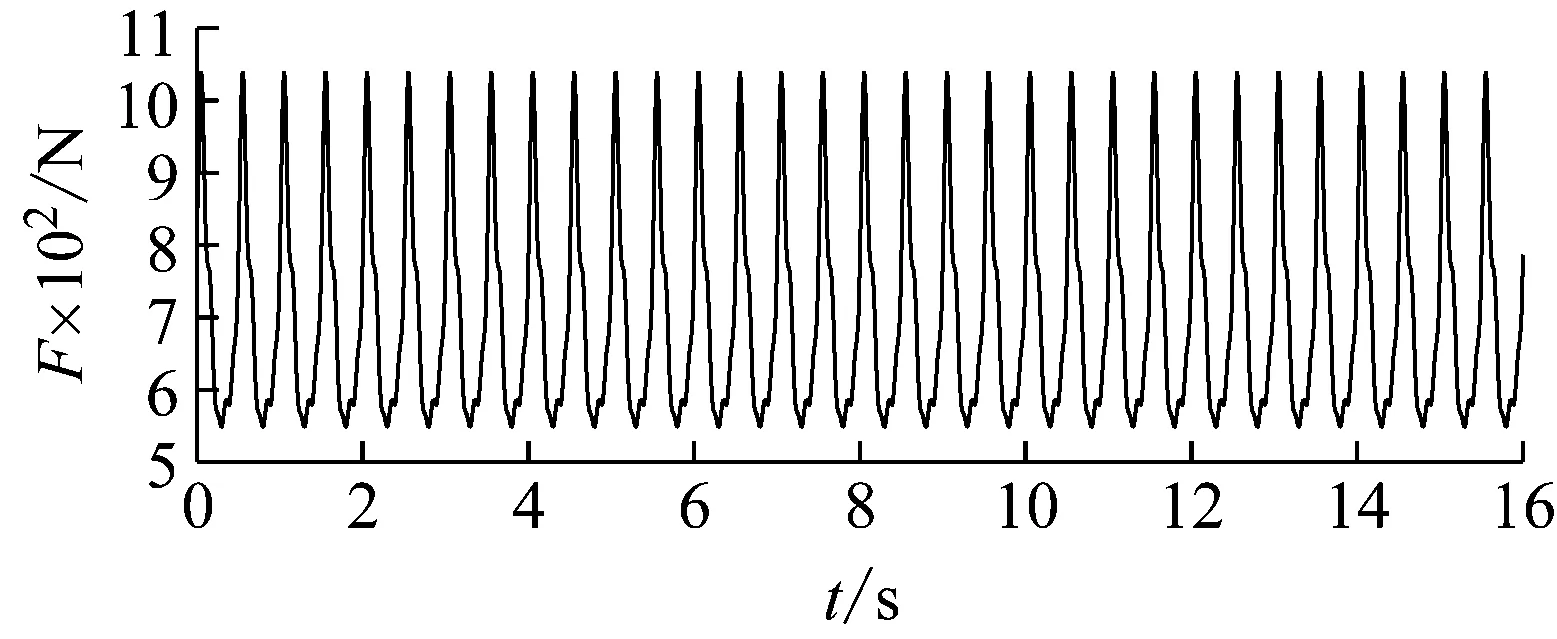
(a) 連續步行荷載時程

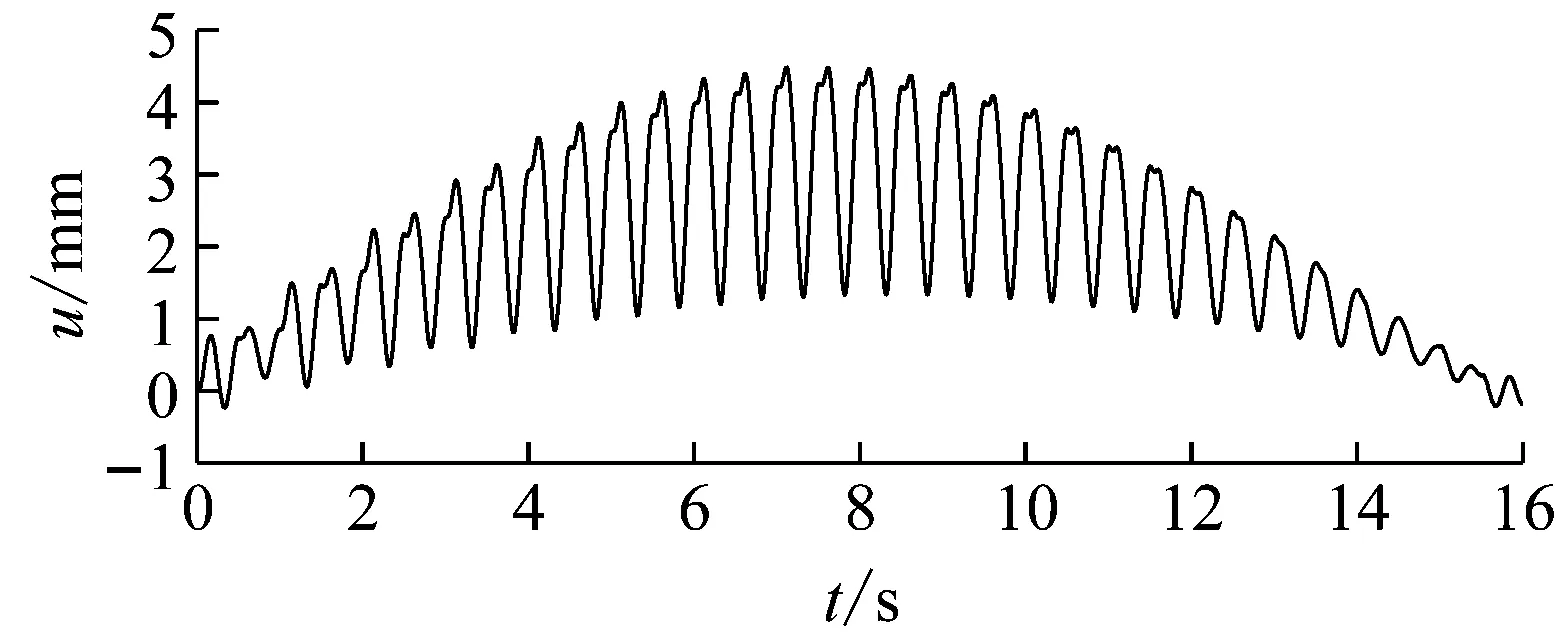
(b) 跨中位移響應時程

對于步行荷載的施加，算例采用陳雋等[13]提出的單人連續步行荷載傅里葉級數模型，其動載因子和相位的數值如表3所示。

荷載模型參數的識別方法及識別過程已經在前一節詳細描述。

2.2 識別結果

為評價兩階段識別方法在識別精度和效率上的優劣，同時進行了一次識別全部參數的GA計算，稱為一次識別法。為了檢驗算法的穩定性，避免出現局部收斂現象，將遺傳算法重復運行三次，最優的參數集是基于目標函數最小值的原則選定的。表4中顯示了系數的識別結果對比；表5是對兩種算法運算效率的對比；圖3、圖4則由荷載時程、傅立葉譜及結構響應時程等方面進行了對比。

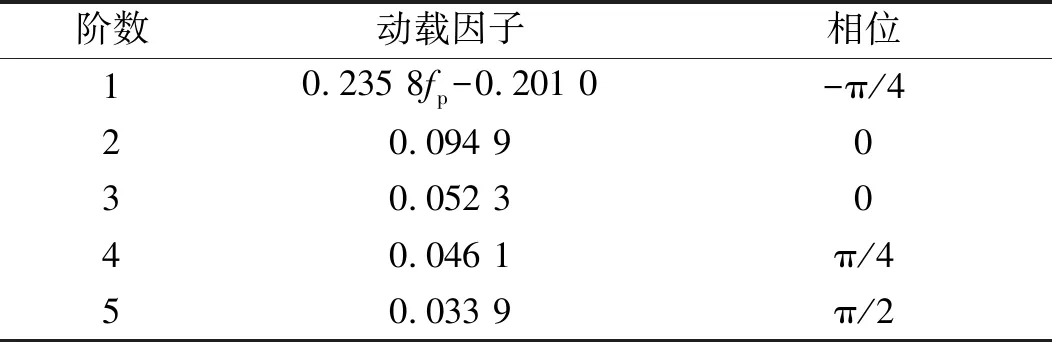
表3 傅里葉級數模型的動載因子和相位

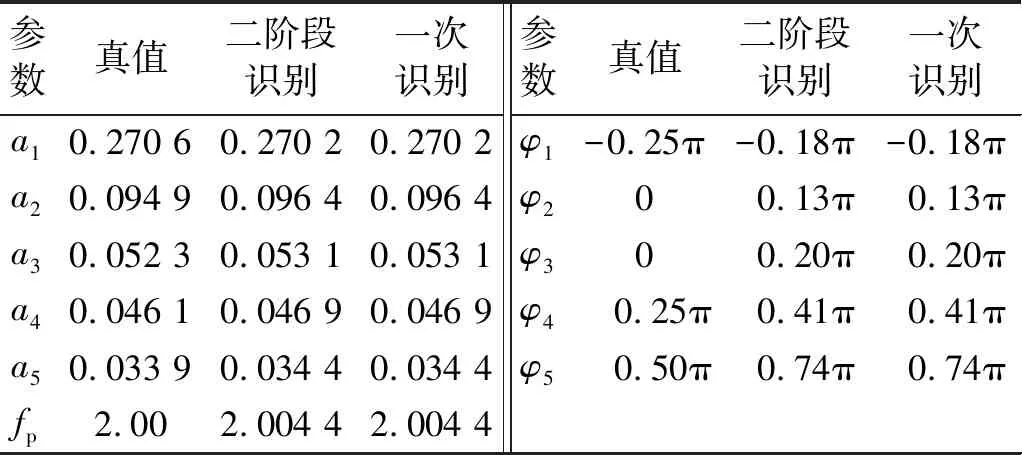
表4 識別結果對比

表5 算法效率對比

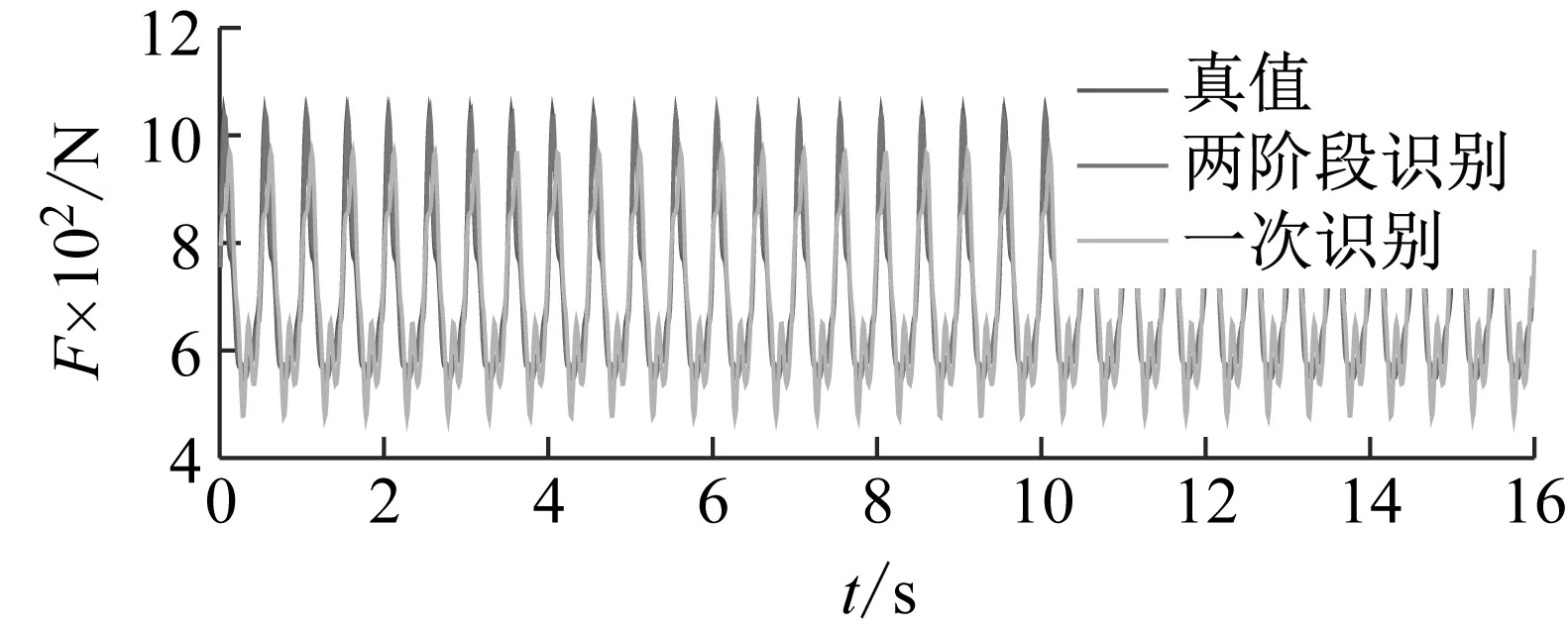
(a) 連續步行荷載時程

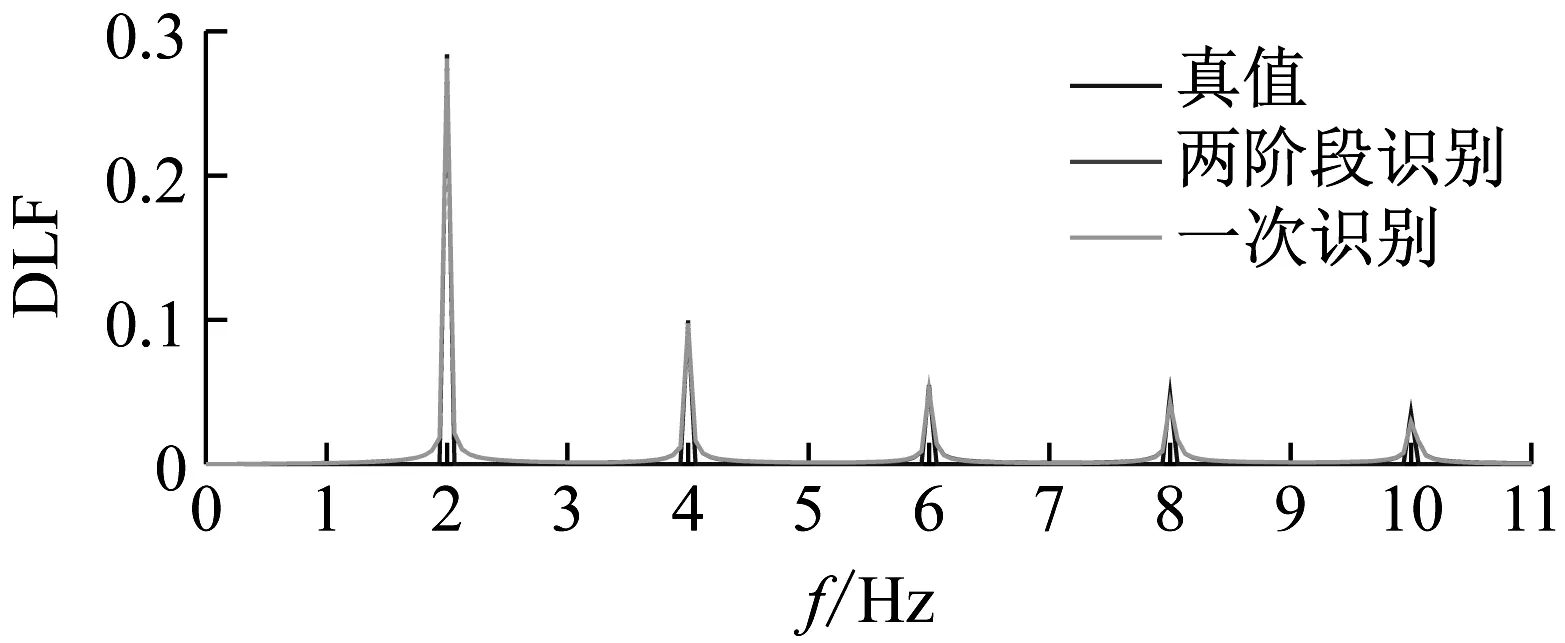
(b) 傅里葉幅值譜

從表4中可以看出，兩種方法對于動載因子和步頻的識別結果一致，識別誤差均在允許范圍之內，三條曲線在傅里葉幅值譜中的對比近乎一致，但相位識別精度一般。

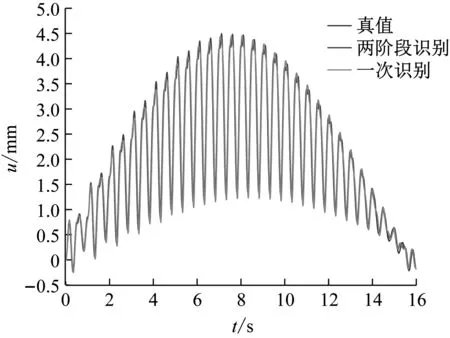
圖4 位移響應時程對比

從圖3和圖4中可以看出，兩種方法相位識別結果的不同造成了荷載曲線明顯的差異。其中，兩階段方法的結果在荷載時程曲線及結構位移響應方面與真值更為接近。從表5的對比可以得出，兩階段方法的計算效率較一次識別法提高50%以上。在進行重復多次識別后發現，兩種方法的動載因子及步頻識別結果皆表現穩定；對于相位的識別結果，兩階段方法表現穩定，但一次識別法相對離散(表6)。其原因可能是一次識別法的參數過多，導致其編碼長度過長，使算法的計算效率降低，增加了局部收斂的概率。綜合以上因素，推薦采用兩階段識別方法進行步行荷載參數的識別。

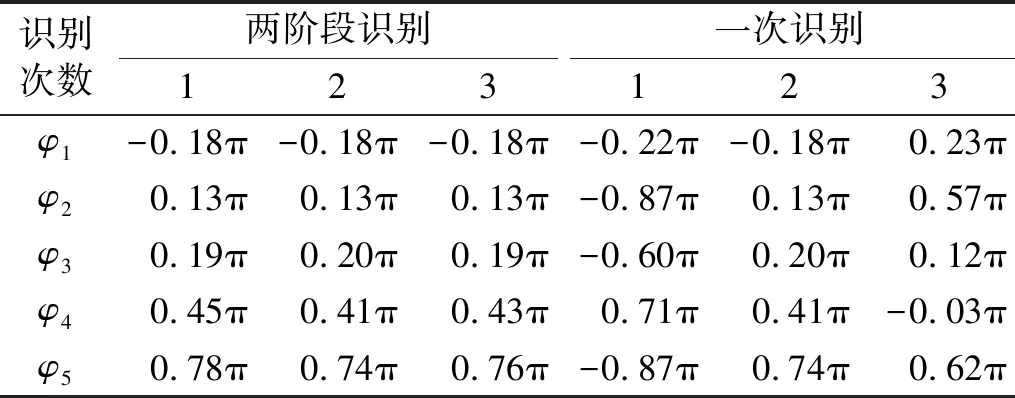
表6 多次相位識別結果對比

3 實測荷載的識別

3.1 實測步行荷載數據來源

本節采用的9條不同步頻的步行荷載時程數據皆來自于測力跑步機獲得的測量結果。測試者為女性，身高160 cm，體重558 N。采樣時間間隔為0.005 s。對實驗數據進行統計，得到如表7所示的實驗信息。

在實驗中，測量過程難免會受到白噪聲的影響。為抑制和防止白噪聲的干擾，需要對步行荷載的時程數據進行濾波處理。采用butter濾波器，濾波階數為5階，截止頻率為Wn=2×20/200。處理后的荷載時程曲線如圖5所示。

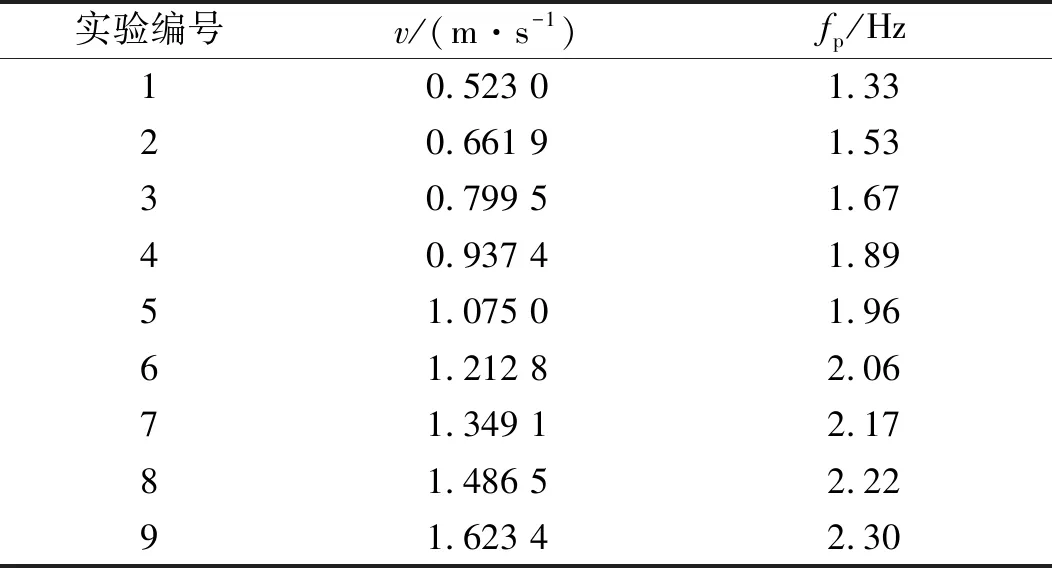
表7 實驗數據基本信息

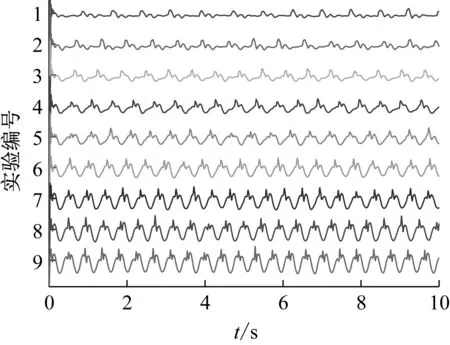
圖5 濾波處理后的實測步行荷載時程曲線

實驗方法、實測荷載參數的識別方法及識別過程與上節荷載模型相同，在這里就不再贅述。

3.2 識別結果

對9條步行荷載時程數據全部進行參數識別，其識別結果與測量曲線擬合結果對比如表8、表9和圖6、圖7所示。

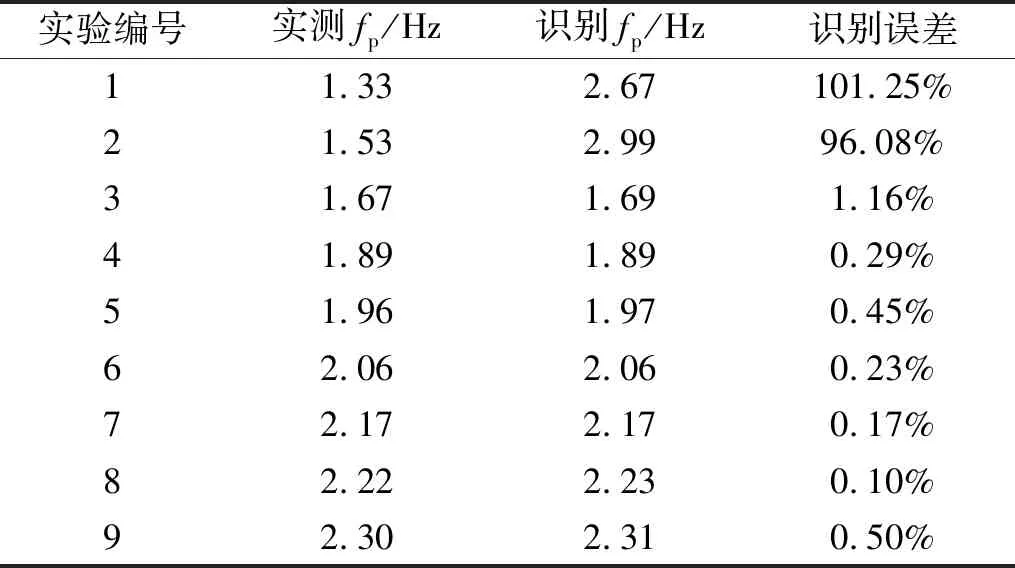
表8 步頻對比

由以上結果可以得出，除實驗編號1、2外，其他步行荷載的識別精度均在誤差允許范圍之內。考慮到人正常行走的頻率范圍是1.5～2.0 Hz，兩階段識別方法具有適用性。對于步頻較低的情況，由于非正常步態造成荷載曲線較強的非周期性(圖5曲線1、2)，導致算法的識別效果不理想。具體參數看，占步行荷載能量主導地位的前3階的動載因子識別效果均較好。以上結果顯示，兩階段識別方法可用于實際步行荷載的參數識別。

表9 動載因子和相位對比

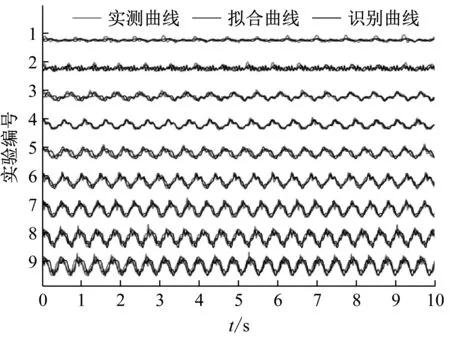
圖6 模擬曲線與實測曲線荷載時程對比

Fig.6 Comparison of load time history between simulated curve and measured curve

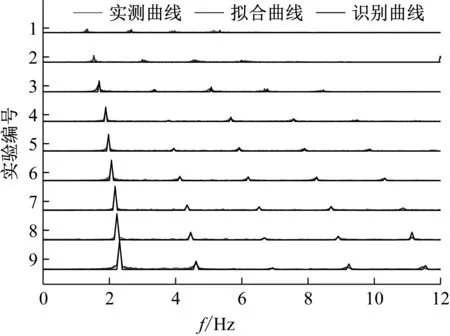
圖7 模擬曲線與實測曲線傅立葉譜對比

4 結 論

從利用結構響應去研究步行荷載特性的角度出發，本文提出了采用兩階段遺傳算法識別步行荷載模型參數的方法。第一階段采用結構位移反應譜一致作為目標函數，識別動載因子、步行頻率等荷載能量的總體要素；第二階段采用結構位移時程一致作為目標函數，識別荷載相位角等局部要素。對步行荷載模型以及實測荷載的具體應用表明，兩階段識別方法可行，對初始參數不敏感，在正常步頻范圍內可以較為準確地獲得荷載前5階的相關參數。兩階段法相較一次識別方式，計算效率提升，并可有效避免局部收斂的問題。

本文將GA這一已經比較成熟的識別方法用于步行荷載的識別，驗證了單人荷載建模的可行性。由于建立在給定荷載模型的基礎上，方法沒有直接考慮HSI。對于可能存在HSI效應的結構，本文方法可給出“響應等效”意義上的等效荷載，通過與剛性地面上荷載模型參數的比較，可進一步研究HSI的影響。此外，本文結果表明，可由結構響應獲得人群荷載作用下的等效單人荷載，從而為研究人群荷載模型提供了反問題建模的新思路。