基于EWT和修正Morris法的抽水蓄能電站主進水閥自激振動研究

李紅輝， 周建中， 張勇傳， 許顏賀， 田弟巍， 王齊飛

(華中科技大學 水電與數字化工程學院，武漢 430074)

抽水蓄能電站機組的振動分為水力、機械和電磁三類[1]，而水力振動又可分為強迫振動引起的水力共振和自激振動兩類[2]。擾動頻率與引水系統頻率接近將導致水力共振[3],索麗生等[4]、周建旭等[5]對現有水電站中的水力共振現象做了研究，提出以振蕩水流分析線性理論為基礎的水電站水力共振分析方法。自激振動則是由系統自身的不穩定因素引起，管道上游閥門或下游閥門均可導致系統發生自激振動[6]。

國內外學者對自激振動現象做了很多研究，從水力阻抗角度研究抽水蓄能電站機組可能產生自激振動的判別條件以及相應的不穩定區域。應用非線性振動理論分析抽水蓄能電站產生自激振動時的幅頻特性，得出抽水蓄能電站機組自激振動由多個衰減因子為正的振動模式疊加而成。葉復萌等[7]、朱淵岳等[8]、張紹春[9]采用特征線法對抽水蓄能電站自激振動事故進行研究，結合實例分析一致認為，自激振動可能是由柔性閥門密封漏水問題引起的，但未探明對主進水閥自激振動有重要影響的關鍵性能參量。

目前，在國內已建成的34座抽水蓄能電站中，發生不同程度主進水閥自激振動現象的電站已經達到4座，占比為12%，并且在“十三五”期間，隨著大批抽水蓄能電站建成投產，該問題會愈加嚴重，這將嚴重影響電站的安全運行。為保障機組和電力系統安全穩定 ，亟需開展對主進水閥自激振動機理研究。為此，本文提出一種基于流體瞬變流理論、經驗小波變換法與修正Morris法相結合的研究方法，并以國內某抽水蓄能電站為研究對象,進行自激振動機理研究，采用瞬變流理論建立抽水蓄能電站過水系統數值仿真模型[10]，采用經驗小波變換法(EWT)分析信號，驗證仿真模型的有效性，并首次引入Morris參數篩選法，探究主進水閥自激振動的影響因素，測算、分析其對自激振動的影響程度和敏感程度，具體研究思路如圖1所示。

圖1 主進水閥自激振動機理分析框架

1 主進水閥自激振動機理分析

抽水蓄能電站過水系統中主進水閥漏水普遍存在。根據主進水閥漏水過流特性曲線是否存在負斜率段，可以分為剛性閥門和柔性閥門。

在閥門關閉后，如果其漏水量隨著壓力的增加而增加，則稱之為剛性閥門，其漏水量

(1)

式中：k為常數。

在閥門關閉后，如果其漏水量會隨著閥門前后壓差的增大而減小，則稱之為柔性閥門，其漏水量

k1=πDx0

k2=πDρgAf/k

(2)

式中：D為閥門直徑，x0為閥門前后差壓為0時的密封間隙，Af為閥門密封蓋的面積，k為閥門密封的彈性系數，ρ為水的密度。

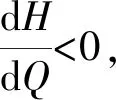
抽水蓄能電站主進水閥在正常運行時，密封性能良好，主進水閥屬于剛性閥門，不會發生自激振動現象。若主進水閥密封破壞成為柔性閥門，其關閉后，有一個微小擾動引起主進水閥的滲漏面積減小，滲漏量減小，由水擊理論可知，滲漏面積減小導致上游管道水壓增大，而該壓力增大將進一步增大主進水閥密封的受迫壓力，并減小滲漏面積，于是又導致上游管道壓力進一步增大；當半周期后由水庫端反射回到主進水閥的水擊波，使主進水閥工作密封壓力減小，滲漏量增大，上游管道負壓會進一步增大。該過程會隨著水擊波沿壓力管道來回傳播。正負水擊壓力的振幅將不斷增大，最終可能導致主進水閥自激振動的發生。

圖2 剛性與柔性閥門的漏水特性

2 主進水閥自激振動建模

基于特征線法建立包含主進水閥柔性閥門在內的抽水蓄能電站過水系統精細化數值仿真模型，從時域的角度對抽水蓄能電站主進水閥柔性閥門漏水引起的自激振動進行分析。

2.1 特征線法理論

基于分布參數理論的特征線(Model of Characteristic, MOC)是目前應用最廣泛的求解有壓管道非恒定流的方法。抽水蓄能電站有壓過水管路動量方程和連續方程描述如下。

動量方程

(3)

連續方程

(4)

對以上兩式列寫特征線水頭連鎖方程如下。

沿正特征線+C(即水錘波傳播方向與水流方向相同)：

HP=Cp-BPQP

(5)

沿負特征線-C(即水錘波傳播方向與水流方向相反)

HP=CM+BMQP

(6)

其中

CM=HB-BQB

(7)

CP=HA+BQA

(8)

BP=B+Cf|QA|

(9)

BM=B-Cf|QB|

(10)

BM=B-Cf|QB|

(11)

B=a/(gA)

(12)

Cf=fΔx/(2gDA2)

(13)

式中：a為波速，A為管道截面,f為摩阻系數，D為管道截面直徑。

2.2 過水系統數值模型

以國內某抽水蓄能電站為例，建立其過水系統數值模型，其管路布置如圖3所示。

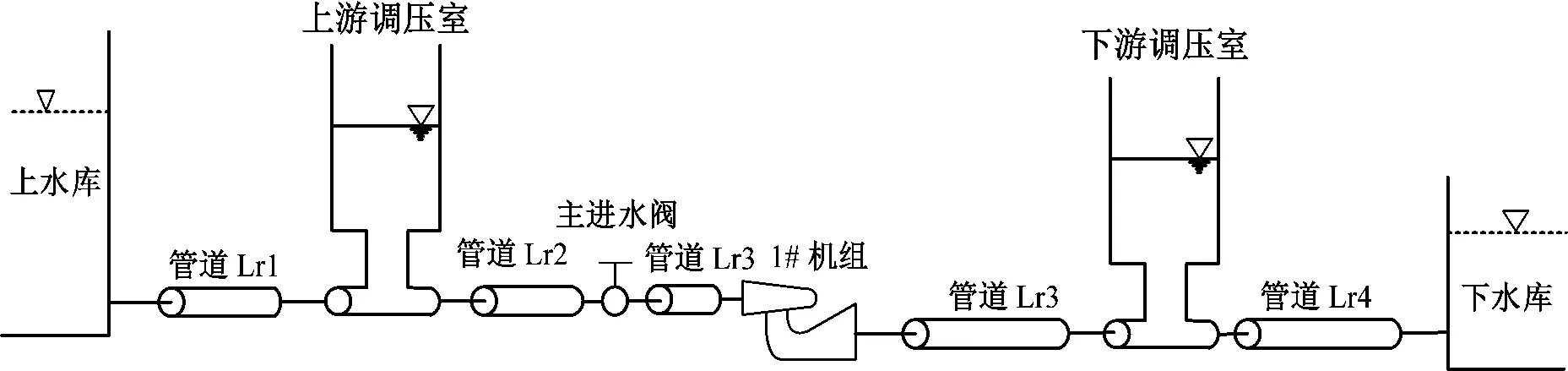
圖3 過水系統管路分段圖

由圖3可知，以上下游水庫、上下游調壓室、主進水閥、水泵水輪機為邊界條件，將電站整個過水系統分為5部分，根據式(3)和式(4)，對每部分管道及邊界列寫特征線方程，通過迭代求解可得到每個節點的流量及水頭變化。抽水蓄能電站過水系統數值仿真模型建立的重點和難點主要是主進水閥的建模，國內外學者大都是將主進水閥作為一個剛性閥門進行建模。為了讓數值仿真模型能精確模擬主進水閥的自激振動過程，本文將其作為一個柔性閥門進行建模，建立抽水蓄能電站過水系統的精細化模型。

2.3 主進水閥自激振動數值仿真

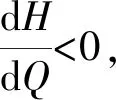
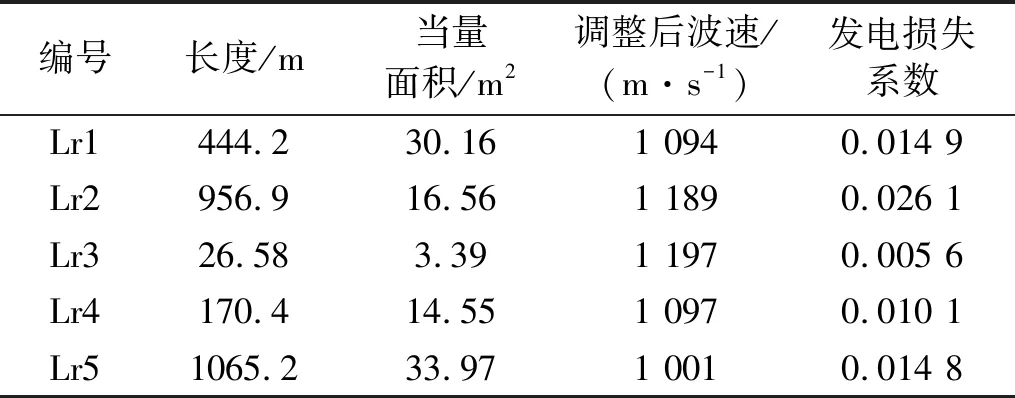
表1 過水系統各分段管路物理參數表

根據過水系統數值模型仿真計算，得到主進水閥上游側水頭隨時間的變化曲線，如圖4所示。

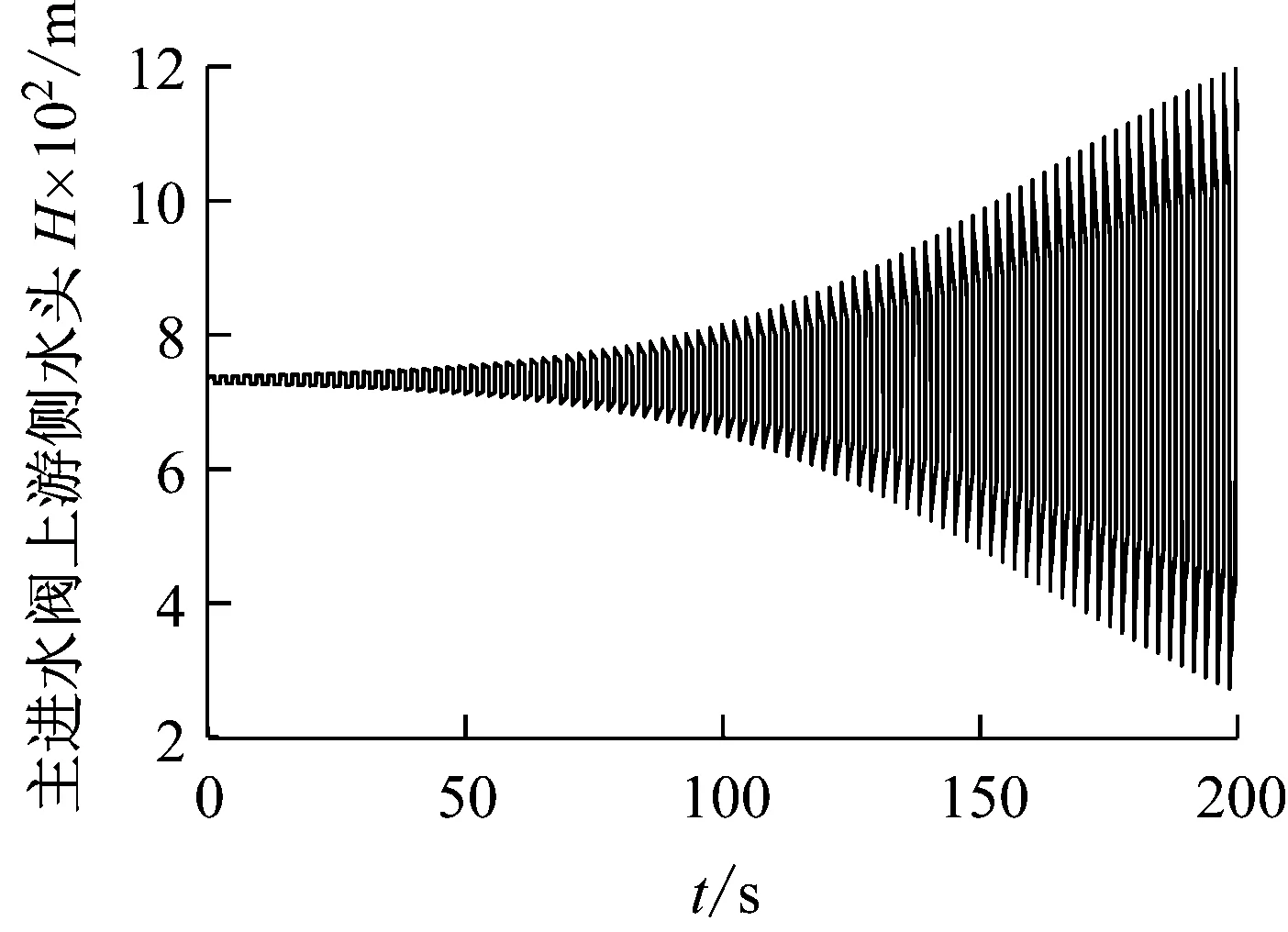
圖4 主進水閥上游側水頭隨時間的變化

由圖4可知，主進水閥在柔性閥門條件下產生自激振動，初始主進水閥上游側水壓振動幅度較小，但隨著時間推移，其振動幅度迅速增大，到200 s時其振動幅度已經達到910 m。如果不及時將自激振動消除任由其發展，最大值可以達到靜水壓力的2倍[11]，將會嚴重威脅電站安全。

3 主進水閥信號分析及數值模型驗證

針對抽水蓄能機組主進水閥設備運行時發生的自激振動問題，本文首先對自激振動信號進行采樣，獲得原始信號波形，再采用經驗小波變換法(EWT)[12-16]獲取自激振動信號和數值仿真信號的特征頻譜，最后將其進行對比分析，以驗證數值模型的有效性[17]。

EWT是2013年Gilles主要針對經驗模態分解(EMD)沒有完備的理論基礎、模態混疊、端點效應等[18]問題提出的。EWT實質是將原信號進行傅里葉變換 并對得到的傅里葉頻譜進行分割劃分，然后建立一組適合每個劃分后的傅里葉頻譜的小波濾波器組并對其進行處理。

將原信號的頻率范圍為[0,π]的傅里葉譜劃分為N個連續的區間Λn，相鄰兩個頻帶的邊界由ωn表示，其中ωn為信號傅里葉譜兩個相鄰極大值點之間的中點，則可表示為

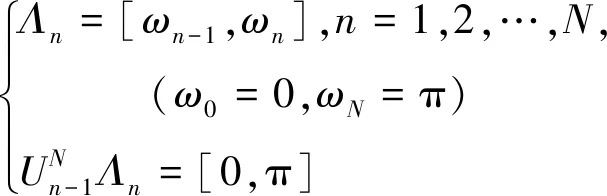
(14)

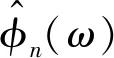
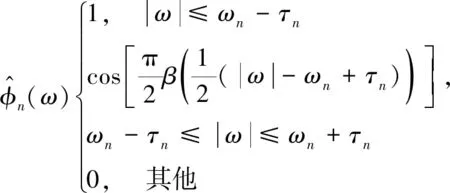
(15)

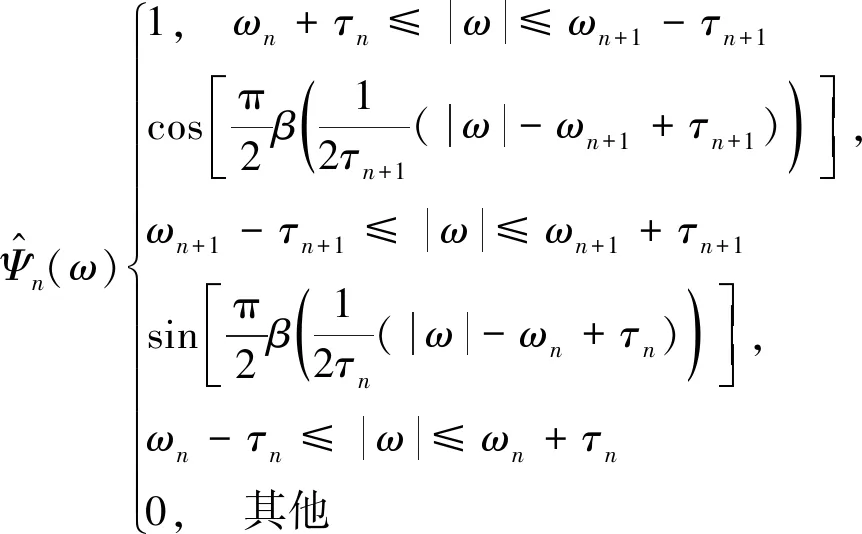
(16)

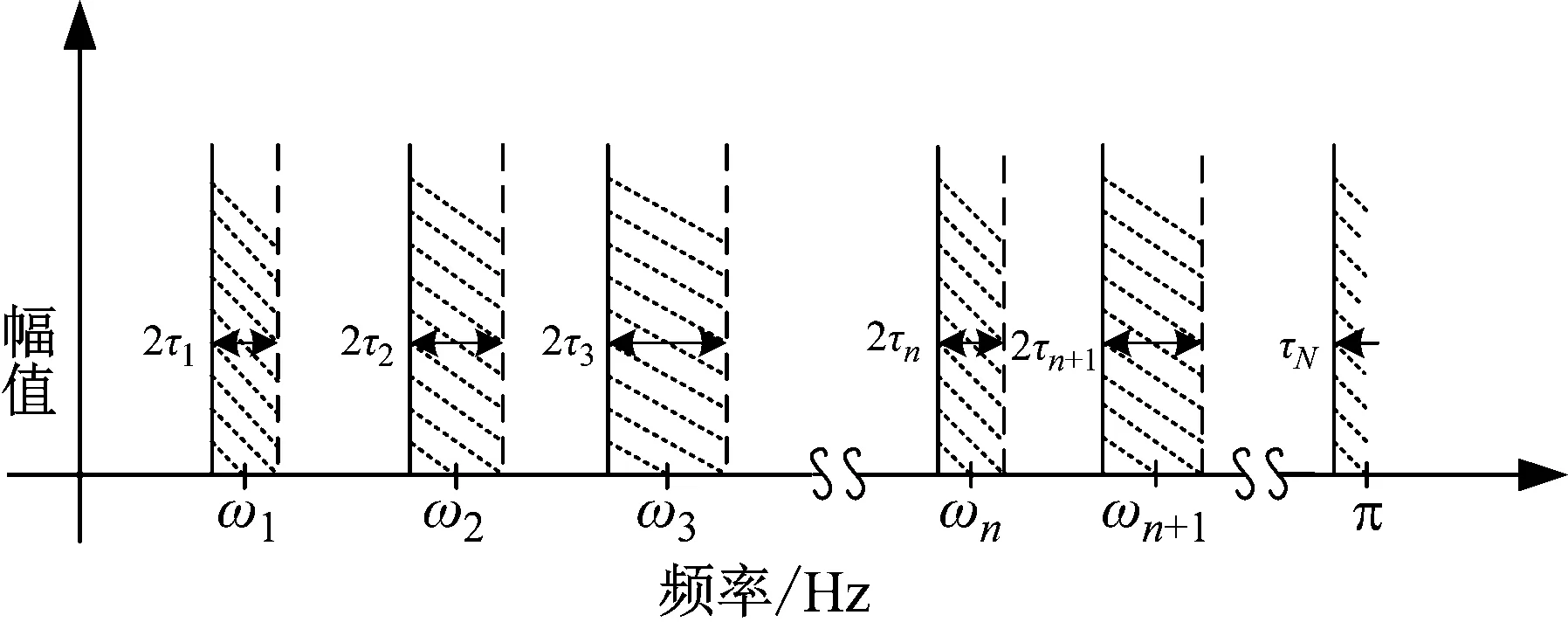
圖5 傅里葉軸分割

式中的τn和β(x)可表示為

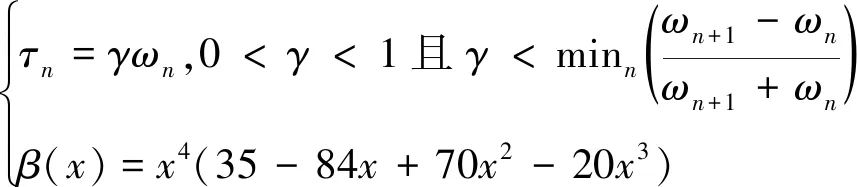
(17)

(18)

基于以上特性，本文采用經驗小波法處理自激振動數據獲取特征頻譜，其優點是繪制傅里葉頻譜圖和Hilbert譜圖時，只保留高頻低幅分量，使得頻譜圖的尺度更精確、更直觀。

將抽水蓄能電站監測系統采集到的主進水閥自激振動的數據進行經驗小波變換繪制傅里葉頻譜圖和Hilbert譜圖，并與模型仿真數據對比，如圖6、圖7所示。

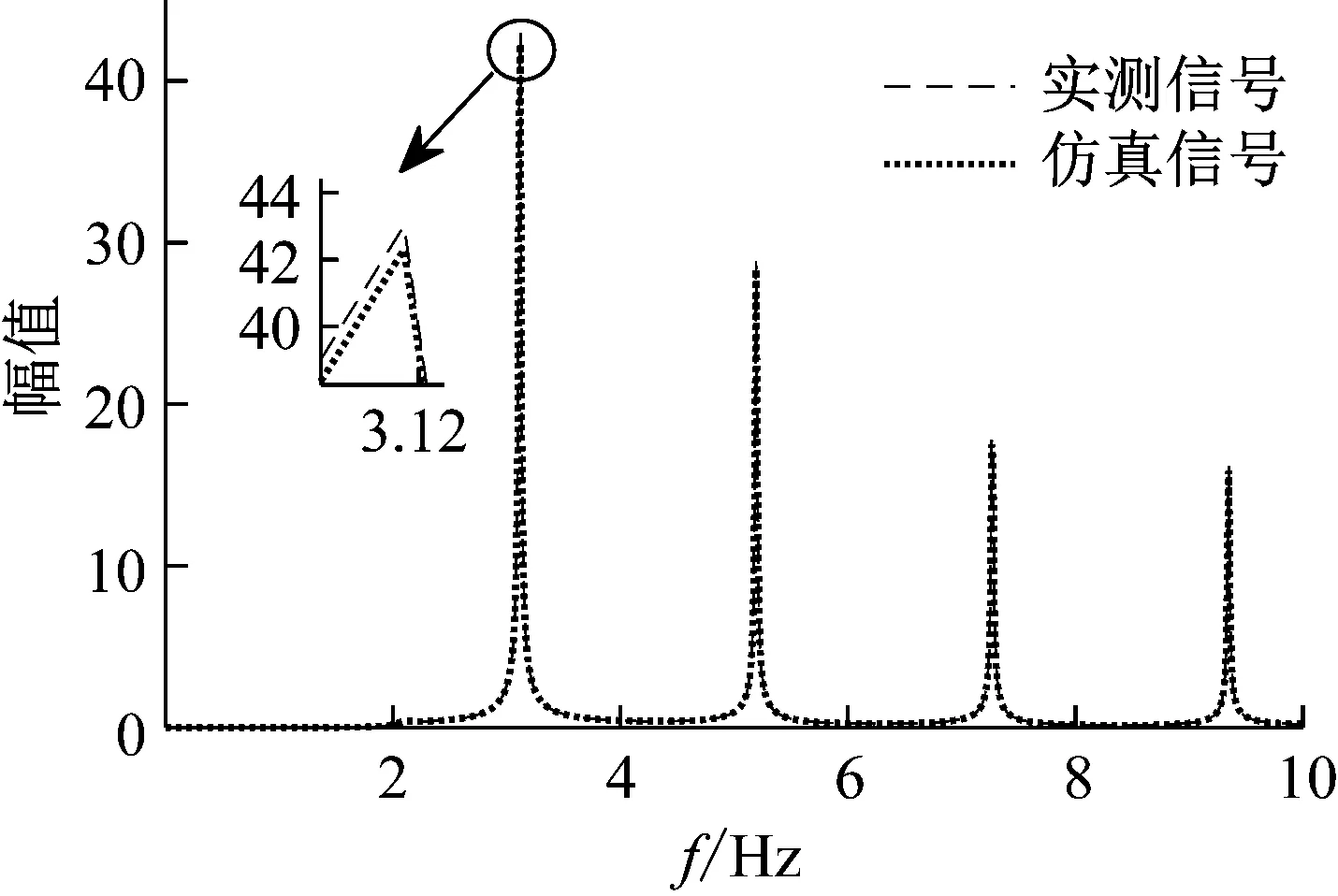
圖6 實測信號與仿真信號的對比圖

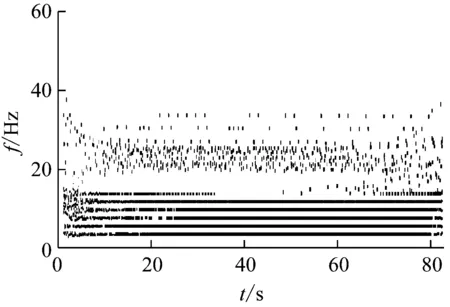
(a) 實測信號的Hilbert譜圖

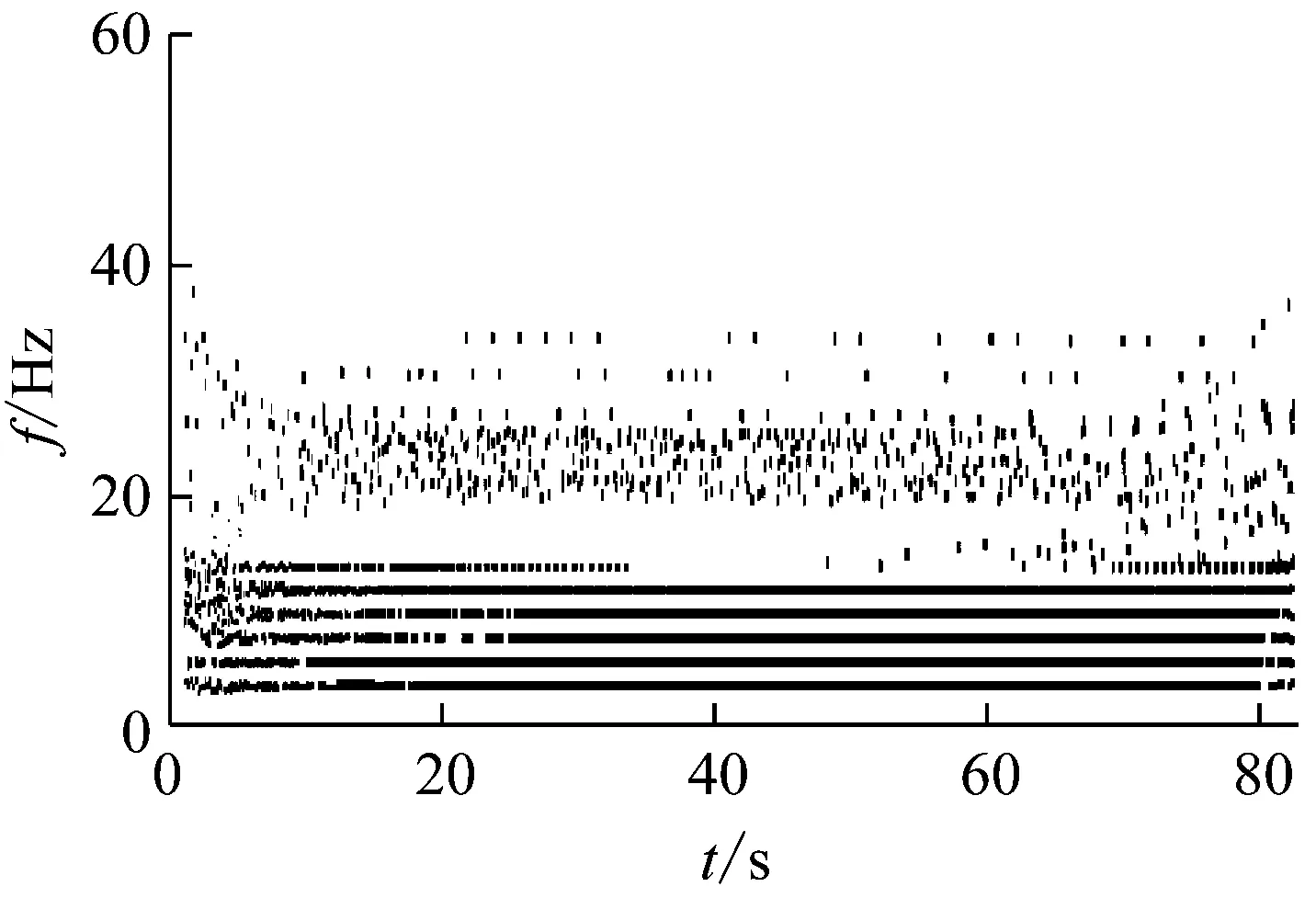
(b) 仿真信號的Hilbert譜圖

由圖6、圖7可知，本文建立的主進水閥自激振動數值仿真模型計算結果與現場實測數據基本吻合，可用于主進水閥特征參量的敏感性分析中。

4 主進水閥特征參量敏感性分析

主進水閥自激振動過程涉及到的參數較多，影響因素復雜多變，為探討主進水閥高程、管道長度，主進水閥閥徑等參數對自激振動的影響，解析不同參數間的關聯程度、各參數對模型輸出的不確定性影響以及貢獻程度，本文采用敏感性分析法，探究對主進水閥自激振動有重要影響的敏感性參數，并分析、測算其對自激振動的影響程度和敏感性程度。

4.1 運用修正Morris法進行敏感性分析

通常敏感性分析包括局部敏感性分析和全局敏感性分析，隨著計算機仿真技術發展，代理模型被逐漸應用到復雜模型的敏感性分析中，本文采用代理模型修正Morris參數篩選法。

修正Morris法作為一種全局敏感性分析方法被廣泛應用，該方法使自變量以固定步長百分率改變，最終敏感性判別因子取多個Morris系數的平均值[20]，其計算公式為

(19)

式中:SN為參數敏感性判別因子;Yi為模型第i次運行的輸出值;Yi+1為第i+1次運行的輸出值;Y0為參數調整后計算結果的初試值;Pi為第i次運行模型后參數值相對于校準后初始參數值的變化百分率;Pi+1為第i+1次運行模型參數值相對于校準后初始參數值的變化百分率;n為模型的運行次數。

修正Morris法根據參數的SN值，將其敏感性劃分為以下4類[21]。

(1) 若參數的敏感度值|SN|≥1，則該參數是高敏感參數;

(2) 若參數的敏感度值0.2≤|SN|<1，則該參數是敏感參數;

(3) 若參數的敏感度值0.05≤|SN|<0.2，則該參數是中等敏感參數;

(4) 若參數的敏感度值0≤|SN|<0.05，則該參數是不敏感參數。

本文選取輸水管道的長度，主進水閥閥徑以及主進水閥閥門間隙等10個參數進行敏感性分析，對其中一個參數分別以70%、80%、90%、110%、120%、130%進行修改，其余參數均保持不變，以計算該參數對主進水閥自激振動的敏感度值，其計算結果如表2所示。

根據表2，下庫水位敏感度值<0.05，為不敏感性參數；主進水閥高程、主進水閥閥徑、主進水閥密封間隙、主進水閥閥門密封蓋面積、主進水閥密封材料和上庫水位的敏感度值<0.2，為中等敏感性參數；管道長度、主進水閥閥門間隙和管道的水擊波速的敏感度值<1，為敏感性參數。

4.2 探究敏感參數對自激振動的具體影響

由敏感性分析探明對主進水閥自激振動影響較大的性能參量是有壓過水系統的管道長度，管道的水擊波速和主進水閥閥門間隙。為探究其對主進水閥自激振動的具體影響，本文采用控制變量法設置三個方案。

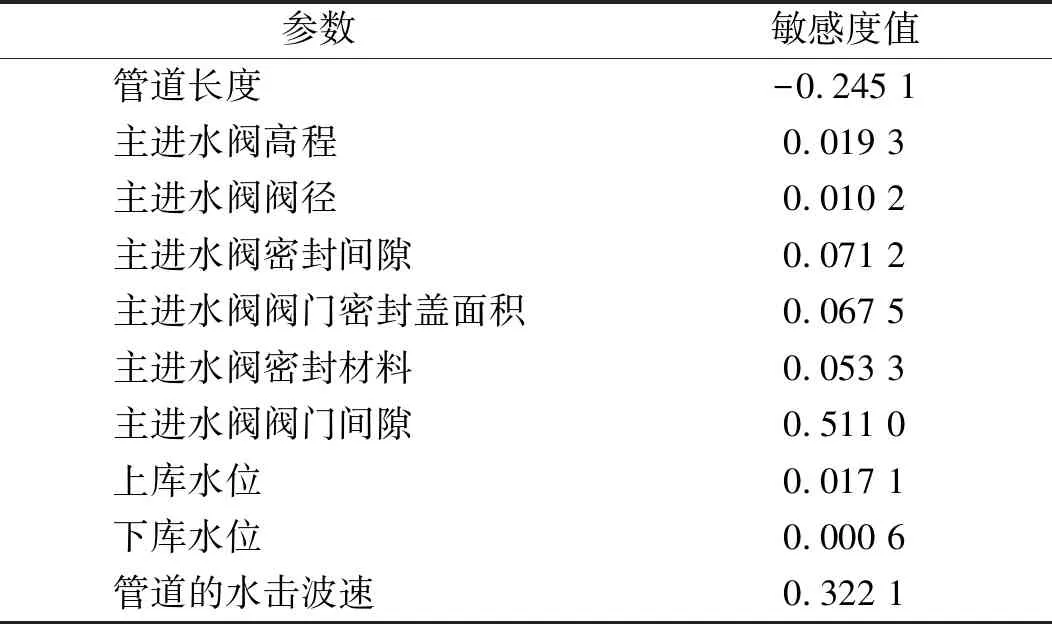
表2 過水系統參數對自激振動的敏感度值

方案1 將管道Lr2改為756 m，其余參數均不改變，其計算結果如圖8。

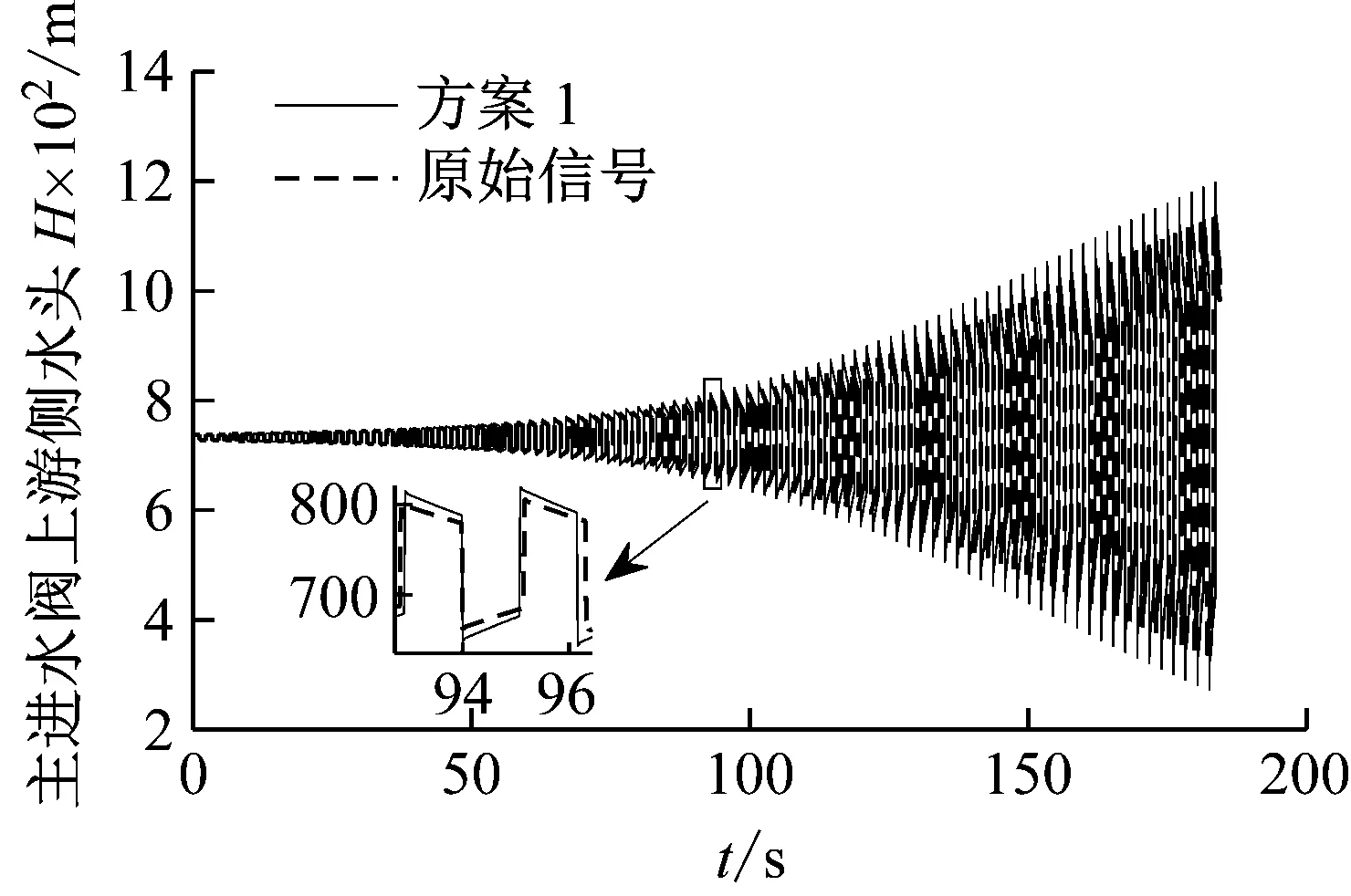
圖8 方案1主進水閥上游側水頭隨時間的變化

方案2 將主進水閥的閥門間隙增加1.1倍，即主進水閥漏水量提高1.1倍，將系數k1,k2擴大為原來的1.1倍，其余參數不變，其計算結果如圖9。

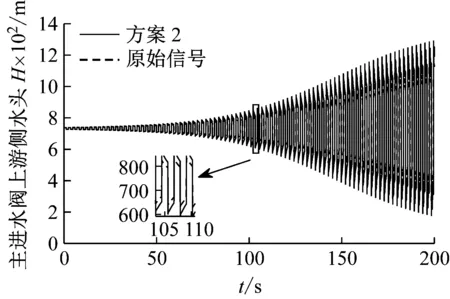
圖9 方案2主進水閥上游側水頭隨時間的變化

方案3 將管道Lr2更換為材料為B610CFHQL2的管道，由于抽水蓄能電站壓力較高選用鋼襯，則其水擊波速為1 030 m/s，其余參數均不變，其計算結果如圖10。

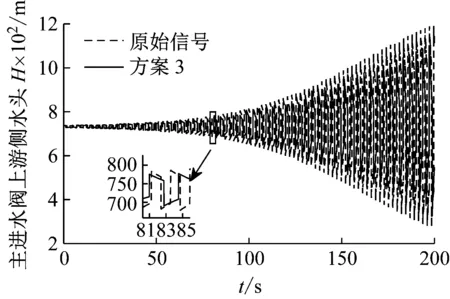
圖10 方案3主進水閥上游側水頭隨時間的變化

由圖8可知，當過水系統的管道的長度縮短后主進水閥自激振動的幅值大幅增加，周期縮短，自激振動發展的速度急劇增大。故可通過增加過水系統管道的長度，以減緩自激振動發展的速度，減輕自激振動的影響。

由圖9可知，主進水閥閥門間隙增大，即閥門的漏水流量增大時，主進水閥自激振動的周期變化較小，但自激振動振幅增長速率及幅值明顯增大。故可通過改進工作密封特別是密封盤根的結構、材料，以減小主進水閥閥門間隙，從而抑制自激振動幅值增長速率，減小自激振動的幅值。

由圖10可知，過水系統管道更換為水擊波速較小的材料之后主進水閥自激振動的幅值大幅減少，周期增加，自激振動發展的速度急劇減少。故可以通過更換水擊波速較小的管道材料，以降低自激振動發展的速率，削弱自激振動的影響，并為消除自激振動提供充裕的時間。

5 結 論

針對抽水蓄能電站主進水閥出現的自激振動現象，本文首先結合已投產電站主進水閥的結構及運行特點，構建主進水閥自激振動數值模型，再采用經驗小波分析法驗證了模型的有效性，最后又運用敏感性分析法深入剖析引起主進水閥自激振動的根本原因，解析主進水閥自激振動的演變機理，最終得出如下結論：

(1) 當抽水蓄能電站的主進水閥為柔性閥門時，閥門關閉后其漏水特性符合柔性閥門漏水過流特性曲線，系統失穩會誘發主進水閥自激振動，若由其任意發展，則可導致爆管事故的發生。

(2) 影響主進水閥自激振動主要因素是管道的長度、水擊波速和主進水閥閥門間隙。

(3) 有壓管道的水擊波速及長度對自激振動的振幅增長速率以及周期影響極大; 主進水閥閥門間隙對系統的振幅增長速率及幅值影響大．但對自激振動的周期影響小。