鎖相環環路特性新型分析和優化方法研究

張堉萌，陰亞東，張利紅

(1.福州大學 物理與信息工程學院，福州 350108；2.福建江夏學院 電子信息科學學院，福州 350108)

鎖相環(Phase Locked Loop，PLL)是現代無線電子 系統中的核心部件，可實現純凈頻率源、高頻時鐘恢復和頻率調制解調等功能，廣泛用于各種技術領域中［1-2］。雖然鎖相環技術誕生已久且業界研究成果很多，但由于鎖相環元部件眾多且環路特性復雜，如何優化鎖相環環路而使其在穩定性、鎖定時間、相位噪聲和雜散干擾等性能指標達到最佳仍然是當前鎖相環研究的關鍵之一。

本文將首先對電荷泵Ⅱ型整數分頻鎖相環進行理論推導，將依次對穩定性、鎖定時間和相位噪聲雜散等進行分析，以獲得鎖相環環路的優化方法；進而，利用MATLAB仿真工具對分析結果加以建模仿真驗證；最終基于鎖相環芯片ICS663和分頻器芯片ICS674完成一款鎖相環電路的設計，進而測試不同環路參數下的鎖定時間、相位噪聲和雜散抑制等性能指標。最終的測試結果與理論分析結果相吻合，驗證了理論分析的正確性。

1 鎖相環環路特性的理論分析

1.1 穩定性優化分析

圖1(a)所示為電荷泵型Ⅱ階整數分頻鎖相環電路結構，其主要由鑒頻鑒相器(Phase Frequency Detector，PFD)，電荷泵(Charge Pump，CP)，環路濾波器(Loop Filter，LPF)，壓控振蕩器(Voltage-Controlled Oscillator，VCO)和分頻器(Divider)等構成。鎖相環以負反饋形式利用VCO輸出信號FVCO經過分頻產生的信號FBAK與輸入參考信號FREF之間的相位比較結果，對FVCO進行頻率調整而使 FBAK頻率相位與FREF趨于一致從而進入鎖定狀態。當進入鎖定狀態時，鎖相環輸出信號FVCO頻率fVCO=NfREF，其中N為分頻器分頻系數，fREF為FREF的頻率，因此fREF決定了整數分頻鎖相環的最高頻率分辨率。

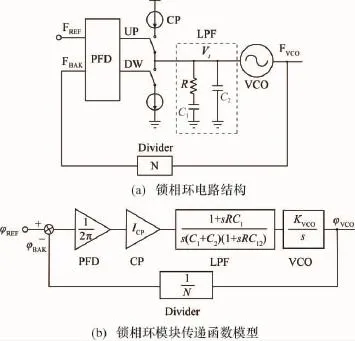
圖1 鎖相環電路結構和傳遞函數模型

電荷泵型Ⅱ階整數分頻鎖相環環路傳遞函數模型如圖1(b)所示。其為典型3階負反饋系統，因而可能存在穩定性問題。其環路開環傳遞函數表示為

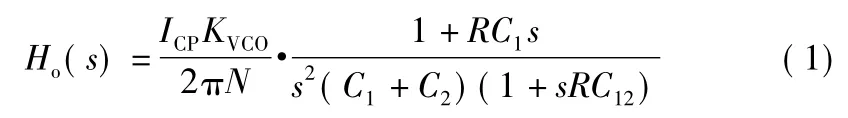
式中，ICP/2π為PFD和電荷泵傳遞系數；KVCO為VCO的電壓頻率轉化系數；C12=C1C2/(C1+C2)。從式(1)可以看到，PLL開環傳遞函數包含了一個零點ωZ=1/RC1和一個非零極點ωP=1/RC12。

從穩定性角度出發，當使 Ho(s )為1時的截止頻率ωC處于ωZ和ωP之間時，環路穩定與否關系密切。當ωC變化時相位裕度可表示為

分析式(2)可知，在零極點固定的情況下，當 ωC=

從式(3)可知，PMopt與LPF中的電容的比值有著密切關系。工程上一般取PMopt=60°能夠獲得較好的環路性能，可求得C1/C2≈13，此時環路濾波器參數為

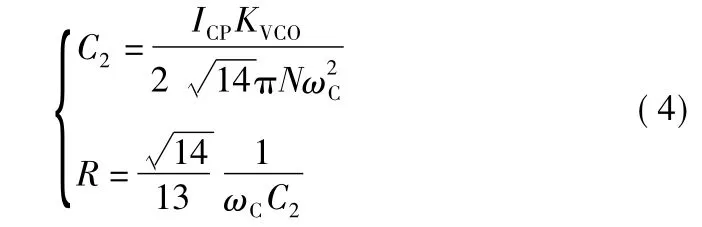
1.2 鎖定時間優化分析

鎖定時間(tlock)亦稱為穩定時間，是反映PLL性能的重要指標。現有研究成果為簡化分析過程視PLL整個鎖定過程為線性變化過程，單純地通過求解PLL閉環傳遞函數的階躍響應而得到鎖定時間［3-5］。當鎖相環初始頻率/相位差較小時，該模型能夠較為精確地描述鎖定時間，但初始頻率/相位差較大時，其得到的鎖定時間與實際情況之間存在較大誤差。圖2為相同環路參數下鎖相環線性模型與考慮非線性特性的真實行為級模型兩種情況下鎖定時間對比。從圖可知，單純采用線性模型獲得的鎖定時間與實際情況存在明顯誤差。因此，有必要深入分析鎖相環環路特性，提出更精確的環路鎖定時間計算模型。

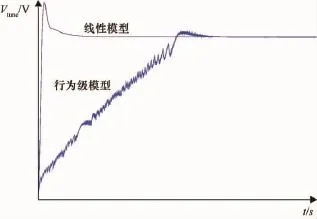
圖2 線性模型和行為級模型的仿真鎖定時間對比

通過研究發現，PLL鎖定時間tlock可分為兩個階段：①當反饋信號FBAK與參考時鐘FREF之間頻率/相差較大時，PFD輸出將飽和而驅使PLL進入非線性狀態；②當誤差小于一定范圍時，PFD退出飽和狀態，此時可近似認為PLL處于線性狀態。因此，PLL鎖定時間應分為兩部分：

式中，ts1和ts2分別對應非線性和線性兩個階段所持續的時間。當PFD輸出飽和時電荷泵將對LPF中的電容進行持續充電/放電，因此ts1可表示為

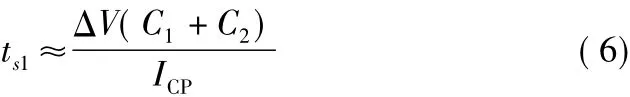
式中，ΔV為初始狀態最終鎖定狀態下VCO控制電壓之間的差值。在最佳環路相位裕度狀態下即ωC=

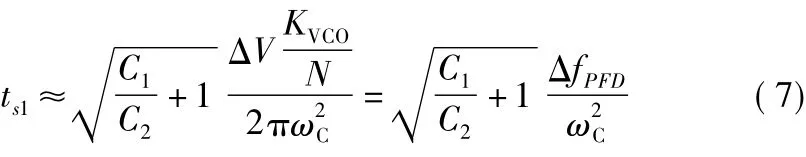
式中，ΔfPFD為非線性階段PFD輸入端的初始頻率誤差。而線性狀態下的鎖定時間可表示為［1］

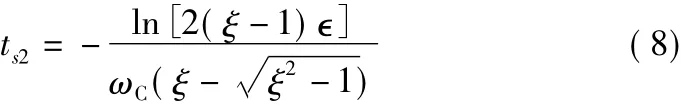
式中，?為線性階段PFD輸入端初始相位誤差。對比式(7)和式(8)可知，兩種模型下鎖定時間存在明顯差異：非線性模型中鎖定時間與ω2C成反比，而線性模型中鎖定時間只與ωC成反比。

1.3 相位噪聲與雜散優化分析

相位噪聲是評價鎖相環性能優劣的重要指標，因此考察鎖相環環路對其輸出相位噪聲的影響至關緊要［6-9］。圖3為PLL的相位噪聲模型，其噪聲來源包括了輸入參考時鐘相位噪聲nREF(s)、電荷泵中電流噪聲nCP(s)、環路濾波器中電壓噪聲nLPF(s)、壓控振蕩器相位噪聲nVCO(s)和分頻器相位噪聲nDV(s)等5個部分，最終的輸出總相位噪聲為各噪聲貢獻之功率和。通過推導分析可得到PLL環路中各種噪聲對總噪聲的貢獻如表1所示。從中可知，除VCO相位噪聲在環路中呈現高通特性外，其他模塊噪聲均在環路中表現為低通特性。考慮到實際電路中VCO噪聲往往起主導作用，因此需要盡可能地提高ωC來抑制VCO噪聲從而改善PLL相位噪聲指標。

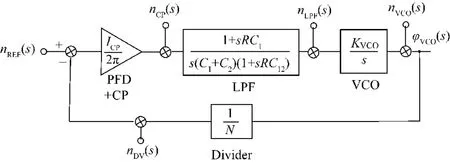
圖3 鎖相環噪聲模型

表1 各噪聲貢獻的函數表達

此外，由于PFD和電荷泵的失配等非理想特性，當環路鎖定時PLL實際上將處于動態平衡狀態，其電荷泵仍將進行周期性的充放電，從而使PLL輸出中包含參考雜散(Reference Spur，RS)成分而惡化相位噪聲指標。該雜散干擾可以看成在電荷泵輸出電流上疊加了頻率為參考時鐘頻率fREF的周期性沖擊脈沖iSPR(t)。

RS可視為PFD/電荷泵噪聲而在環路中表現為低通特性。根據3階鎖相環環路特性，最終輸出中雜散的噪聲貢獻可表示為

其中，ISPR(ω)為iSPR(t)的傅里葉變換頻域變換形式。為抑制雜散干擾，通常雜散頻率ωREF應當滿足ωREF＞＞ωP＞ωC［7-9］。則雜散對PLL輸出的影響可表示為

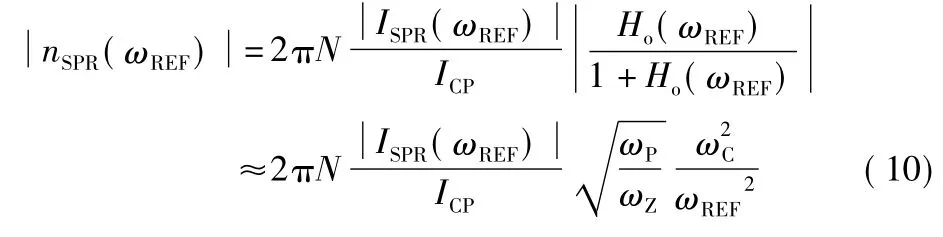
雖然式(10)指出降低ωP/ωZ可降低雜散強度，但通常需要保持較高的ωP/ωZ，以確保環路具有較好的相位裕度。另一方面可知，雜散強度與ωC/ωREF項的平方成反比，降低ωC/ωREF可以有效地抑制雜散干擾。

綜合以上分析可知，鎖相環環路截止頻率ωC對鎖相環性能具有重要影響。從相位噪聲指標出發，提高ωC可有效的抑制Ⅱ型鎖相環中占主導的VCO噪聲，同時迅速地縮短鎖定時間；然而ωC的提高將嚴重削弱鎖相環的雜散抑制能力。綜合考慮，ωC≈(1/5～1/10)ωREF是較為合理的取值范圍。

2 鎖相環仿真驗證

2.1 穩定性的仿真驗證

基于MATLAB仿真平臺，構建了鎖相環開環和閉環模型，選取輸入參考信號為100 kHz，分頻比為200，則最終輸出為20 MHz；同時根據芯片IC663指標選擇了 ICP=2 μA，KVCO=2π ×200M rad/V；為使環路 ωC=2π ×2k rad·s-1，PM=60°，根據前文推導結果可計算濾波器參數為R=23 kΩ，C1=90 pF，C2=7 pF。將以上參數代入MATLAB鎖相環模型中計算可知，其中ωC=12.5 krad/s，PM=60°，仿真結果與計算結果一致。

2.2 鎖定時間與雜散的仿真驗證

基于MATLAB構建了鎖相環行為級電路模型，通過改變環路帶寬和輸入參考信號頻率，獲得如圖4所示的PM一致而ωC和fREF不同時環路LPF輸出電壓的瞬態仿真結果。圖中(a)和(b)的ωC相同，而(a)的fREF為(b)的一半，這意味著(a)的初始頻率/相位差亦為(b)的一半，而仿真結果顯示其鎖定時間(1.8 ms)也大致為(b)的一半(4 ms)。在fREF保持不變情況下，對比(a)和(d)兩條曲線可知，ωC降低一半時鎖定時間則延長至4倍。同時，對比(b)和(c)兩條曲鎖定時間基本一致。這些仿真結果均與前文分析結果吻合。

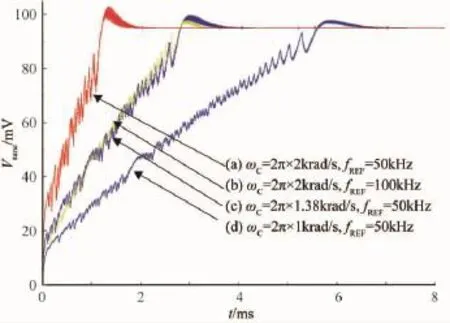
圖4 各種參數下的鎖定時間仿真結果

圖5 為4種情況下PLL輸出信號的頻率變換，可以看到(a)情況下雜散強度最大達-58.2 dBc；而在散強度下降6 dB為-64.2 dBc；(b)和(d)由于 ωC/ωREF相同且為(a)的1/2，因而其雜散強度下降12 dB均為-70 dBc；從中可以發現，仿真結果與前文推導一致。

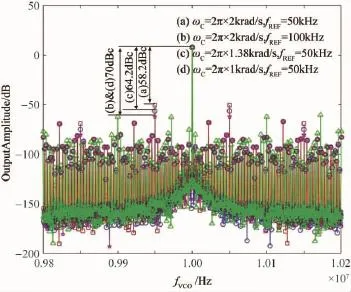
圖5 各種參數下雜散強度仿真結果

2.3 相位噪聲仿真驗證

相位噪聲仿真驗證中，通過IC663芯片手冊獲取了VCO的噪聲數據［10］，同時其他噪聲采用熱噪聲模擬其他噪聲源。圖6所示為不同環路下相位噪聲仿真結果。其中圖6(a)為其他參數不變，ωC變化時PLL相位噪聲仿真擬合曲線。由于VCO噪聲的主導作用，ωC越小，PLL帶內相位噪聲越明顯；另一方面PLL帶外噪聲卻基本保持不變；這與前文中鎖相環噪聲分析基本一致。通過仿真發現，ωC不變時不同分頻比N(圖6(b))或不同電荷泵電流ICP(圖6(c))的鎖相環相位噪聲特性基本保持不變。綜上可知，在VCO噪聲其主導作用下，PLL輸出相噪特性基本只取決于ωC。

圖6 環路參數變化對鎖相環相位噪聲影響的仿真結果

3 電路設計與測試驗證

基于鎖相環ICS663芯片和分頻器芯片ICS674設計了PLL電路并制作了PCB板，其實物如圖7所示。其中鎖相環的分頻系數、環路濾波器參數均通過板上開關切換進行更改。

圖7 鎖相環電路PCB實物照片

由于實際電路中，輸出參考信號的高次諧波很容易耦合至PLL輸出中，從而影響雜散的測試。為了減少這種諧波干擾，測試中設置分頻系數為3(IC674分頻系數必須不小于3)，以使PLL輸出頻率盡量接近參考頻率，而此時參考頻率設置為fREF=1 MHz。然后分別測試了 ωC為2π×5k rad/s和 ωC=2π ×10k rad/s兩種情況下的雜散強度，如圖8所示。由圖可知，ωC=2π×5k rad/s時雜散強度為-40.46 dB而ωC=2π×10k rad/s時雜散強度升高為-27.72 dB，升高約為12.7 dB，測試結果與式(10)預測基本相符。

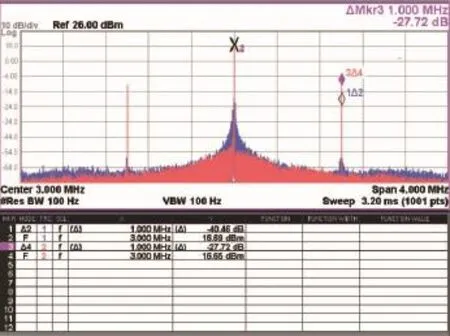
圖8 不同ωC時雜散測試結果

利用Agilent MSO3024示波器測試了以上兩種ωC下的鎖相環啟動過程中LPF輸出電壓變化情況，其測試結果如圖9所示，從圖中可以看到鎖定時間由736 μs延長延長了約4倍至2.76 ms，證明了鎖定時間與ωC成反比。

最終利用Agilent N9020A信號分析儀完成了PLL相位噪聲的測試。圖10(a)為不同ωC下相位噪聲測試結果，從圖中可以看出ωC越高則帶內噪聲越低，而帶外噪聲基本一致。由于無法改變ICS663芯片內部參數，因而本論文選擇通過改變ICS674分頻系數來測試ωC相同而分頻系數N不同時的相位噪聲特性，其結果如圖10(b)所示。可以看到，當N在50/100/200之間發生變化時，PLL輸出相位噪聲輸出結果基本保持不變，以上結果均與分析及仿真結果吻合。

4 結束語

首先對Ⅱ型電流泵整數分頻鎖相環環路特性進行了分析推導，推導結果顯示合理選擇環路濾波器電容比值可使相位裕度實現最優化，鎖定時間與環路截止頻率ωC平方成反比，雜散強度與(ωC/ωREF)2成正比等重要結論。進而開展了基于Matlab的鎖相環環路仿真驗證和基于鎖相環芯片ICS663的鎖相環電路設計與測試工作，仿真結果與實際電路測試結果均與本文鎖相環理論分析結果相符。

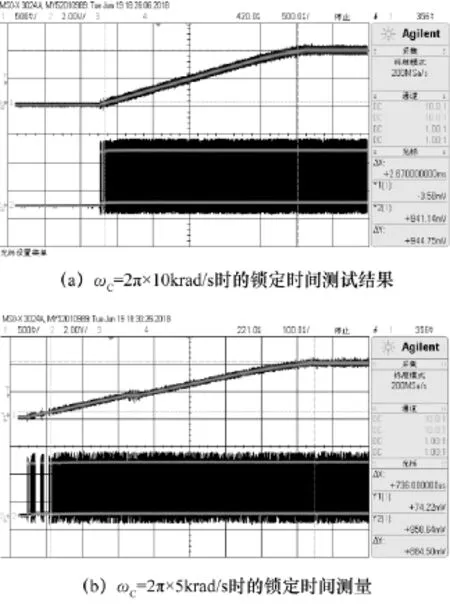
圖9 不同ωC下鎖定時間測試結果

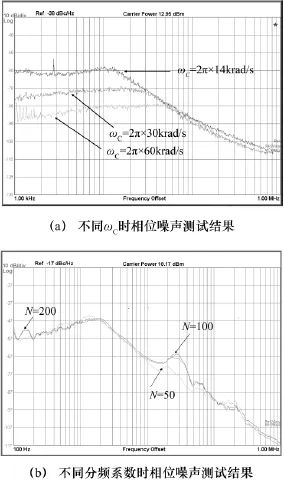
圖10 相位噪聲測試結果