PID控制原理在語音信號盲源分離中的應用

嚴發(fā)鑫，徐 巖，湯旻安

(蘭州交通大學電子與信息工程學院，甘肅蘭州 730070)

語音分析所用的信號通常是在實際場合下采集到的，是多個未知源信號組成的傳感器信號，這給語音信號的分析帶來極大的不便。盲源分離是在語音源信號和混合方式缺乏先驗知識的情況下，僅通過傳感器接收的信號提取語音源信號。盲源分離給語音分析帶來方便。非平穩(wěn)混合下的盲源分離是一種特殊情形，例如，多個語音源不斷移動的場合下，傳感器接收到的信號是時變的，可視為將語音源信號通過非平穩(wěn)系統(tǒng)混合得到。需根據系統(tǒng)擾動采用在線盲源分離算法實時調節(jié)學習速率，動態(tài)更新分離矩陣。通常采用的在線算法為自適應盲源分離算法。

目前，對于非平穩(wěn)混合系統(tǒng)下的盲源分離研究，陳海平［1］等人提出了在線FastICA算法，通過將傳感器信號分成短時段，在每段內使用傳統(tǒng)的FastICA批處算法，在線實時跟蹤非平穩(wěn)的混合系統(tǒng)。季策［2］等人提出了一種約束算法，該算法利用混合系統(tǒng)的變動對目標函數進行約束，并對約束因子和學習速率自適應調整。張?zhí)祢U［3］等人提出了一種首先實時估計混合矩陣得到性能指數，再基于性能指數對學習速率和動量因子動態(tài)更新的方法。陳海平的方法能有效跟蹤非平穩(wěn)環(huán)境，但由于使用了批處理算法，算法的計算量大，短時段的劃分容易產生誤差。季策和張?zhí)祢U的算法收斂速度快，穩(wěn)態(tài)誤差小，但對算法的等變性考慮不足，算法較復雜。總之，目前采用自適應盲源分離算法并對其優(yōu)化可以較好地實現非平穩(wěn)混合系統(tǒng)下的分離，但算法本質上對系統(tǒng)擾動考慮不足［2］，故非平穩(wěn)混合下的盲源分離仍需進一步研究。

非平穩(wěn)混合下的自適應盲源分離算法需考慮等變性問題，等變性是指盲源分離的性能與混合矩陣無關，即混合矩陣變化時對分離性能不產生影響，能有效保證算法的魯棒性。但一般的自適應盲源分離算法與混合矩陣有關，不能保證等變性，特別是采用預處理的算法［4］。本文首先提出無預處理的自適應盲源分離算法，再基于PID控制原理實時依據非平穩(wěn)混合擾動動態(tài)調整學習速率，提高收斂速度，減小分離誤差，最后進行仿真驗證和性能分析。

1 算法的基本原理

一般正定、線性瞬時混合盲源分離問題按如下方式描述［5］。傳感器信號 x(t)=［x1(t)，x2(t)，…，xn(t)］T是由源信號 s(t)=［s1(t)，s2(t)，…，sm(t)］T混合得到，m、n分別是源信號的數目、混合信號的數目，正定即m=n，線性瞬時混合的傳感器信號記為

式中，A為滿秩的混合矩陣。源信號的估計信號y(t)=［y1(t)，y2(t)，…，ym(t)］T，通過求解估計信號可得到分離出的源信號。

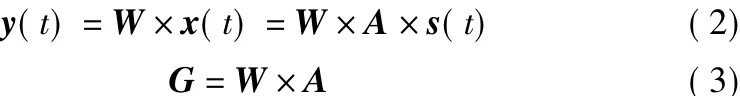
式中，W為滿秩的總分離矩陣；G為全局矩陣。

2 算法的具體實現

2.1 無預處理的自適應盲源分離算法

假設源信號和估計信號都具有單位方差和零均值，并且源信號統(tǒng)計獨立。由于盲源分離不能保證估計信號的幅度為源信號的實際幅度，且分離結束后估計信號的各個分量必須相互獨立［5］，將分離結束后估計信號的自相關矩陣一般化為［6］

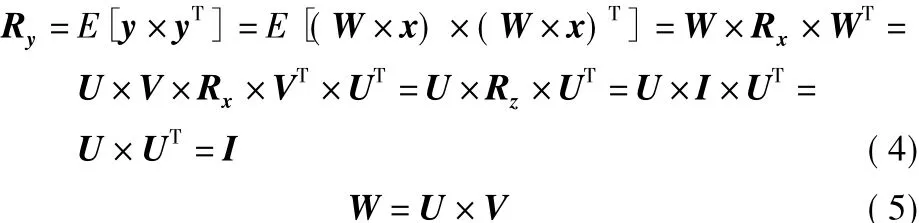
式中，W為總分離矩陣；I為單位矩陣；Rx為傳感器信號的自相關矩陣；U為正交分離矩陣；V為白化矩陣；Rz為傳感器信號白化后的自相關矩陣，Rz=I。采用的目標函數記為［6］

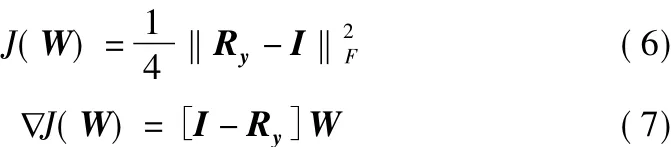
分離矩陣的迭代更新式記為［6］

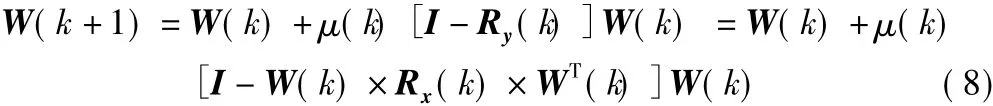
式中，k指代第k步迭代，根據式(4)分離結束后Ry=I，代入式(8)，得 W(k+1)=W(k)，因此最終式(8)是收斂的；μ(k)為第k步的學習速率；Ry(k)為第k步迭代時估計信號的自相關矩陣，Rx(k)為第k步迭代時傳感器信號的自相關矩陣，為便于在迭代過程中計算Rx(k)，用式(9)迭代過程的時間平均近似估計［7］。

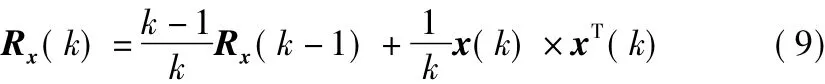
為提高分離過程的穩(wěn)定性，確保迭代快速收斂，用式(10)對矩陣W×Rx×WT標準化。

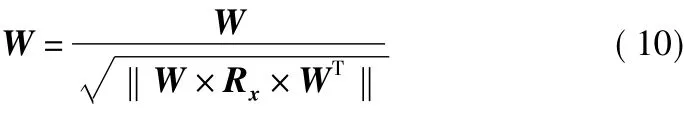
這種無預處理的自適應盲源分離算法可以實現預處理的兩個目標：

①根據式(4)，傳感器信號的二階相關被去除，傳感器信號各個分量相互正交；

②根據式(4)，總分離矩陣簡化為正交分離矩陣，從而算法復雜度降低。

為驗證算法具有等變性，將式(8)的左右兩端都右乘混合矩陣A，根據式(1)可以得到

再根據式(3)可以得到

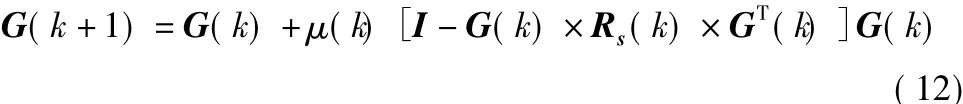
式中，k指代第k步迭代。G(k+1)的更新與混合矩陣A、總分離矩陣W以及傳感器信號的自相關矩陣Rx無關，與源信號的自相關矩陣Rs有關，證明了算法具有等變性。

2.2 PID調節(jié)學習速率

PID控制即比例、積分、微分控制，它因調節(jié)簡單、應用方便、魯棒性較好，廣泛應用于工業(yè)控制，常見的被控量有溫度、液位、壓力等。PID控制的特點是能應用于系統(tǒng)存在變動、精確數學模型不能建立的場合［8］。依據式(8)，基于常規(guī)PID控制模型，建立一種以矩陣W×Rx×WT元素平方的最大值作為實際輸出，以單位矩陣I中元素最大值1作為期望輸出，便于計算機處理的，依據系統(tǒng)變動實時調整學習速率的數字增量式PID控制模型。控制模型如圖1所示。

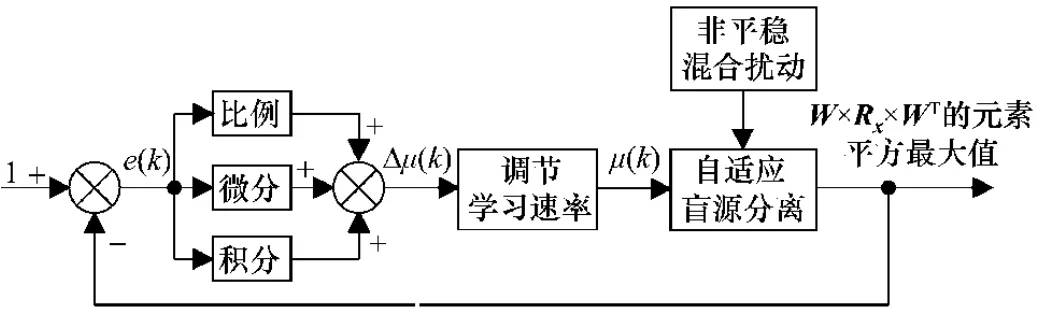
圖1 PID控制模型

圖1 比例運算為Kp［e(k)-e(k-1)］，積分運算為Kie(k)，微分運算為Kd［e(k)-2e(k-1)+e(k-2)］，Kp，Ki，Kd分別對應比例系數、積分系數、微分系數。則學習速率的變化量Δμ(k)記為［8］

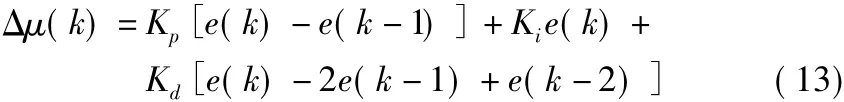
調節(jié)學習速率部分對應常規(guī)PID控制模型的執(zhí)行機構，增量式PID控制計算過程不涉及累加運算，計算復雜度小，計算機容易處理，調節(jié)后的學習速率記為［8］

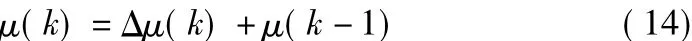
自適應盲源分離部分對應常規(guī)PID控制模型的被控對象。根據調節(jié)后的學習速率，自適應盲源分離算法迭代更新分離矩陣，進而得到系統(tǒng)的輸出值。采用此種PID控制模型可以實時跟蹤系統(tǒng)變動，減小不穩(wěn)定因素對自適應盲源分離的影響，加快分離的收斂速度，減小分離的穩(wěn)態(tài)誤差，提高非平穩(wěn)混合系統(tǒng)自適應盲源分離算法的魯棒性。

2.3 算法實現步驟

①初始化學習速率μ、總的分離矩陣W、自相關矩陣Rx和混合矩陣A；

② 用式(10)對矩陣W×Rx×WT標準化；

③用式(8)迭代更新分離矩陣；

④ 用式(9)估計Rx；

⑤用式(13)計算學習速率的變化量，然后用式(14)計算調節(jié)后的學習速率；

⑥判斷是否收斂，若是進行步驟⑦，否則回到步驟②；

⑦繪制分離前和分離后的源信號波形、系統(tǒng)的響應曲線和性能曲線。

3 仿真和分析

3.1 算法仿真

由于建立的PID控制系統(tǒng)的傳遞函數得不到精確數學模型，故利用經驗法整定PID參數。經驗法PID參數整定原則遵循先“比例”，后“積分”，再“微分”的次序［9］，整定指標為整定后的參數能使所提出的自適應盲源分離算法的分離性能指數PI與零值距離最小，仿真中分別多次改變比例系數、積分系數、微分系數，分別比較歷次穩(wěn)態(tài)時的PI仿真值，取最小值時的比例系數、積分系數、微分系數。依據PID參數整定原則和整定指標選擇最優(yōu)解作為PID參數整定的結果。分離性能指數PI定義為［5］

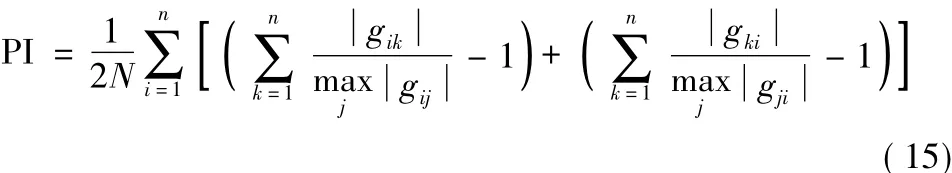
式中，gij為全局矩陣G中的元素陣G的第i行元素絕對值中全局矩陣G的第j列元素絕對值中的最大值。PI值越接近零，分離效果越好。

仿真PC機采用的基本硬件參數為Intel Core i5-3210M，主頻2.50 GHz，內存4 GB。仿真軟件為MATLAB R2015b。選取標準語音庫中的兩路語音源信號s1(t)和s2(t)，分別為firegold.wav和risesun.wav，采樣率8 kHz，采樣點數28000個，長度3.5 s。仿真中用變化的混合矩陣與源信號混合成變化的兩路傳感器信號x1(t)和x2(t)。混合矩陣變化分為緩變和突變兩種情況。μ(0)的取值過小會因前期PI的波動大使分離誤差大，且算法收斂速度慢，過大時系統(tǒng)響應曲線波動大，實際中應依據系統(tǒng)響應曲線和性能指數曲線選定μ(0)的值。W(0)的取值是為了保證迭代收斂后的分離矩陣滿足正交性，宜取單位矩陣乘以一個系數，該系數僅影響算法的收斂速度，實際中應依據算法的仿真時間選定W(0)的值。R(0)的取值不影響仿真結果，可以任意選定。A(0)的取值選擇在［0，1］上均勻分布的隨機值進行隨機混合。在本仿真中綜合選擇適中的值 μ(0)=0.5，W(0)=I×0.5，R(0)=I，A(0)=rand(size(s，1))。

3.1.1 混合矩陣緩變情形下算法仿真

混合矩陣緩變定義為［10］

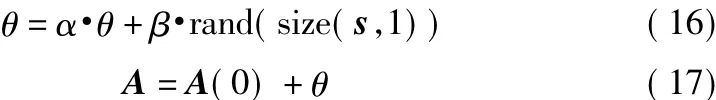
式中，α為遺忘因子；β為控制學習速率。選取經驗值α =0.9，β =0.01。

混合矩陣緩變情形下，PID參數整定結果如圖2所示，PID參數整定后的語音分離結果如圖3所示。

從圖2可以看出，比例系數整定為Kp=0.02，積分系數整定為Ki=0.0000099，微分系數整定為Kd=0.0049。整定后的系統(tǒng)響應速度快，超調量小，穩(wěn)態(tài)誤差小。從整定后的性能指數曲線看前期有小范圍波動，這是由于前期PID控制實時跟蹤系統(tǒng)緩變，不斷調節(jié)學習速率所致。在500 ms后，PID控制系統(tǒng)進入穩(wěn)態(tài)，同時分離趨于收斂，分離的穩(wěn)態(tài)誤差較小。

圖2 混合矩陣緩變情形下PID參數整定圖

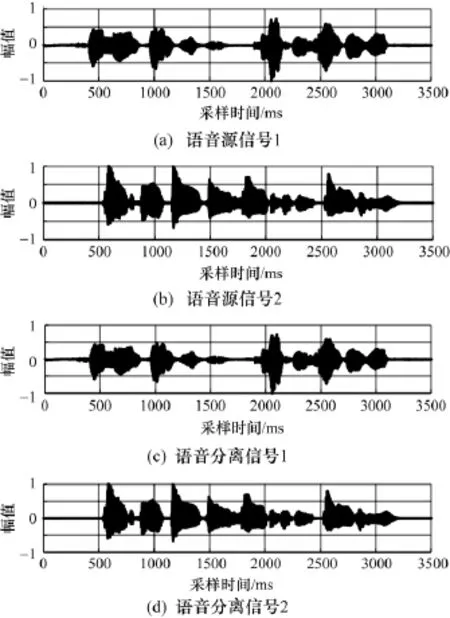
圖3 混合矩陣緩變情形下語音分離結果圖

從圖3可以看出，仿真的語音分離信號和語音源信號接近一致，不僅驗證了PID參數整定合理，還驗證了提出的算法適用于混合矩陣緩變情形下的語音分離。

3.1.2 混合矩陣突變情形下算法仿真

混合矩陣突變定義為［11］

混合矩陣突變情形下，PID參數整定結果如圖4所示，PID參數整定后的語音分離結果如圖5所示。

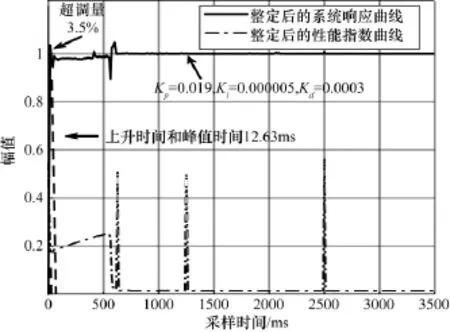
圖4 混合矩陣突變情形下PID參數整定圖

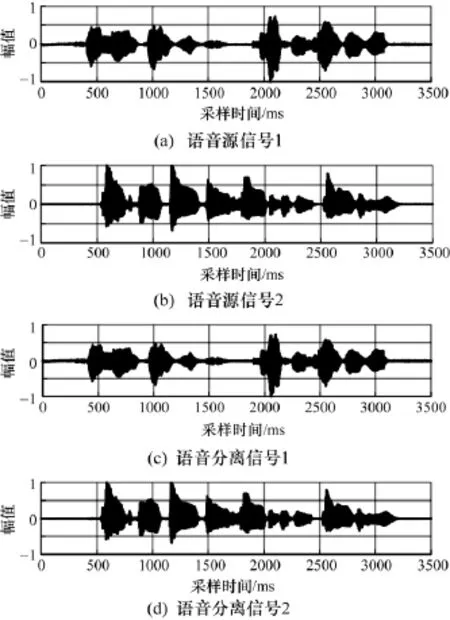
圖5 混合矩陣突變情形下語音分離結果圖

從圖4可以看出，混合矩陣突變情形下，比例系數整定為Kp=0.019，積分系數整定為Ki=0.000005，微分系數整定為Kd=0.0003。整定后的系統(tǒng)響應速度快，超調量小，穩(wěn)態(tài)誤差小。從整定后的性能指數曲線看在 625 ms、1250 ms、2500 ms都出現突變，而前期由于PID控制不斷調節(jié)學習速率，系統(tǒng)快速進入穩(wěn)態(tài)，在625 ms后分離趨于收斂，分離的穩(wěn)態(tài)誤差小。

圖5的分離結果驗證了混合矩陣突變情形下PID參數整定合理，算法適用于混合矩陣突變情形下的語音分離。

本節(jié)分別在混合矩陣突變和緩變兩種情形下合理整定PID參數，并驗證了本文算法在這兩種情形下，整體的分離性能好，收斂速度快，穩(wěn)態(tài)誤差小，受系統(tǒng)擾動的影響小。下面將進一步分析本文算法的性能。

3.2 算法分析

在混合矩陣緩變和混合矩陣突變情形下，分別仿真經典的 Chambers的自適應盲源分離算法［12］和Thomas的自適應盲源分離算法［13］，以及本文算法。對比分析算法的性能指數PI、時間復雜度。在兩種情形下依照Chambers和Thomas分別為算法仿真選取的初值。Chambers算法的參數選擇為μ(0)=10-4，修正因子ρ=10-8，非線性函數f=2tanh，其他參數與本文算法一致。Thomas算法的參數選擇為μ(0)=10-4，修正因子ρ=0.025，遺忘因子α=0.998，非線性函數f=2tanh，其他參數與本文算法一致，本文算法的參數與3.1節(jié)所述一致，仿真條件也與3.1節(jié)所述一致。三種算法在混合矩陣緩變情形下性能指數比較如圖6所示。

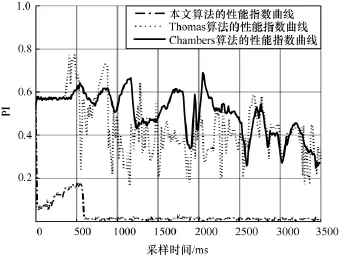
圖6 混合矩陣緩變情形下性能指數比較

從圖6可以看出，混合矩陣緩變情形下，本文算法的性能指數曲線波動比Chambers算法和Thomas算法都小，本文算法能快速進入穩(wěn)態(tài)，穩(wěn)態(tài)誤差小。可見混合矩陣緩變情形下，本文算法性能受環(huán)境變動影響小，能解決提高收斂速度和減小穩(wěn)態(tài)誤差間的矛盾，算法具有等變性。

三種算法在混合矩陣突變情形下性能指數比較如圖7所示。

從圖7可以看出，混合矩陣突變情形下，本文算法的性能指數曲線波動仍比Chambers算法和Thomas算法都小，本文算法收斂速度快，穩(wěn)態(tài)誤差小。可見混合矩陣突變情形下，本文算法性能受環(huán)境變動影響小，能解決提高收斂速度和減小穩(wěn)態(tài)誤差間的矛盾，算法具有等變性。

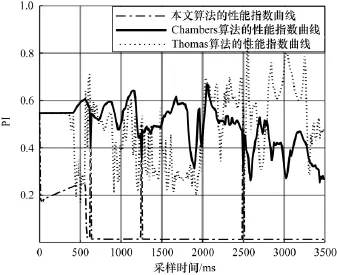
圖7 混合矩陣突變情形下性能指數比較

為進一步比較算法的復雜度，混合矩陣緩變和突變情形下算法各自的運行時間如表1所示。仿真中算法的運行時間以MATLAB的tic、toc函數為組合進行計算，tic函數標識程序開始，toc函數標識程序結束。

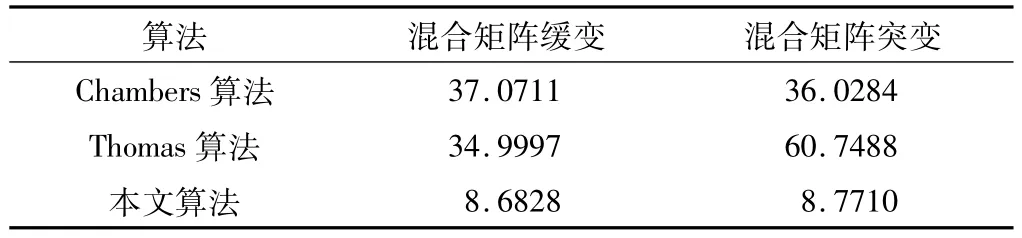
表1 混合矩陣緩變和突變情形下算法運行時間比較表單位：s

表1綜合反映了在混合矩陣突變和緩變兩種情形下，本文算法復雜度都比其他兩種經典算法小。

4 結束語

本文提出了一種基于PID控制原理學習速率動態(tài)更新的自適應盲源分離算法，通過在混合矩陣緩變和突變兩種情形下，對PID參數整定，實現了對學習速率實時調整，算法不需要預處理，減小了復雜度，保證了等變性，整體性能受系統(tǒng)變動的影響小，分離收斂速度快、穩(wěn)態(tài)誤差小。利用MATLAB軟件對算法仿真并分析，驗證了算法的有效性和實用性。比較結果表明，本文算法在混合矩陣緩變和突變情形下，較經典算法優(yōu)勢明顯，可應用于非平穩(wěn)混合下對混合信號進行實時跟蹤，從而分離出相互獨立的源信號，以便對源信號進行研究分析。但算法采用經驗法整定PID參數，隨機性大，存在誤差，尋求更優(yōu)的、更適合于自適應盲源分離算法的PID整定方法是日后研究的方向。