時滯執(zhí)行器飽和Markov跳變系統(tǒng)的有限時間鎮(zhèn)定

張遠敬，彭 力，2

(1.江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院物聯(lián)網(wǎng)應(yīng)用技術(shù)教育部工程研究中心，江蘇無錫 214122；2.無錫太湖學(xué)院江蘇省物聯(lián)網(wǎng)應(yīng)用技術(shù)重點建設(shè)實驗室，江蘇無錫 214064)

Markov跳變系統(tǒng)是一類受內(nèi)部離散事件作用，導(dǎo)致系統(tǒng)參數(shù)隨機變化的特殊混雜系統(tǒng)。同時，實際的控制系統(tǒng)經(jīng)常遭遇來自外界的隨機干擾以及內(nèi)部元器件的損壞，例如航天航空飛行器、通信網(wǎng)絡(luò)、經(jīng)濟系統(tǒng)等［1-2］。基于Markov鏈的隨機特性，衍生了很多實際場景中的應(yīng)用［3-4］，并且由于Markov跳變系統(tǒng)能夠很好地描述受外部干擾等影響的實際系統(tǒng)，因此得到了廣泛的關(guān)注與研究。例如：Senthikumar［5］研究了Markov跳變系統(tǒng)的穩(wěn)定性分析問題。Wu［6］研究了Markov跳變系統(tǒng)的異步濾波問題。

在Markov跳變系統(tǒng)中，狀態(tài)轉(zhuǎn)移概率是決定系統(tǒng)行為的關(guān)鍵因素。考慮到實際過程中，系統(tǒng)的轉(zhuǎn)移概率總是部分未知的。因此，研究具有部分未知轉(zhuǎn)移概率的Markov跳變系統(tǒng)的相關(guān)系統(tǒng)理論是有必要的。到目前為止，這方面的研究已經(jīng)取得了不錯的進展，如Du［7］研究了其系統(tǒng)的穩(wěn)定性，Qi［8］研究了這種系統(tǒng)的狀態(tài)反饋控制器設(shè)計問題，Yang［9］研究了系統(tǒng)的魯棒非脆弱H∞控制等。

在許多實際應(yīng)用中，需要考慮系統(tǒng)在有限時間內(nèi)的行為，系統(tǒng)的狀態(tài)響應(yīng)在有限時間內(nèi)滿足一定的界限。在過去的幾十年里，有限時間穩(wěn)定性或有界性的問題引起了越來越多的關(guān)注。隨著Lyapunov函數(shù)和線性矩陣技術(shù)的發(fā)展，這方面的研究也取得了一定的成果，如Zhang［10］研究了奇異隨機系統(tǒng)的觀測器設(shè)計問題，Zhang［11］針對系統(tǒng)的穩(wěn)定性進行了分析，Amato［12］研究了系統(tǒng)的動態(tài)輸出反饋問題等。

另一方面，在實際的工程系統(tǒng)中，時間延遲和執(zhí)行器飽和始終是導(dǎo)致系統(tǒng)不穩(wěn)定以及性能差的主要原因，尤其出現(xiàn)在交通、化學(xué)反應(yīng)過程以及機器人工程等領(lǐng)域。Zhang［13］提出 Abel引理對時延系統(tǒng)建立穩(wěn)定性條件，Zhang［14］研究了具有時延和執(zhí)行器飽和的切換線性系統(tǒng)的容錯控制問題。近年來，在時滯和執(zhí)行器飽和線性系統(tǒng)方面［15-16］，以及相關(guān)非線性系統(tǒng)控制方面［17-18］都取得了一定的成果。

對于一系列特殊的復(fù)雜隨機系統(tǒng)來說，具有時延和執(zhí)行器飽和的離散Markov跳變系統(tǒng)能夠很好地描述隨機干擾因素，包括突發(fā)性的故障、外部的干擾和環(huán)境因素的突變等。然而，對于這類系統(tǒng)在轉(zhuǎn)移概率部分未知情況下，有限時間控制的研究結(jié)果較少。考慮到上述情況，并考慮具有執(zhí)行器飽和以及轉(zhuǎn)移概率部分未知的離散時滯Markov跳變系統(tǒng)，討論了系統(tǒng)在時延情況下的有限時間鎮(zhèn)定(FTS)問題。

1 系統(tǒng)描述及相關(guān)引理

考慮含執(zhí)行器飽和以及固定時滯的離散時間Markov跳變系統(tǒng)：

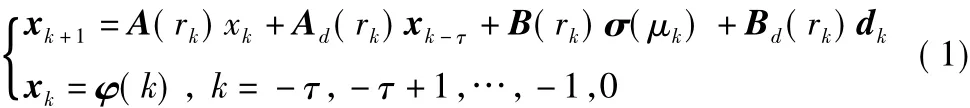
式中，xk∈Rn，μk∈Rm分別為系統(tǒng)的狀態(tài)向量和控制輸入向量；dk∈Rp為未知但有界的擾動信號；xk=φ(k)，k=-τ，-τ+1，…，-1，0為系統(tǒng)的初始狀態(tài)；A(rk)，Ad(rk)，B(rk)，Bd(rk)分別為已知的具有適當(dāng)維數(shù)的與模態(tài)rk相關(guān)的常數(shù)矩陣，其中rk為系統(tǒng)的模態(tài)，在集合S={1，2，…，N}中隨離散時間取值的時齊Markov鏈，其狀態(tài)轉(zhuǎn)移概率定義為

考慮轉(zhuǎn)移概率部分未知的情況，轉(zhuǎn)移概率∏ ={pij}中有部分元素是未知的。對于?i∈S，集合Si=概率的元素集合和未知轉(zhuǎn)移概率的元素集合。如果

在有限時間步長L＞0內(nèi)，未知輸入擾動信號滿足：

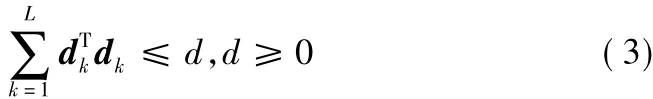
為了方便后續(xù)引用，當(dāng) rk=i時，分別用 Ai，Adi，Bi，Bd來表示 A(rk)，Ad(rk)，B(rk)，Bd(rk)。

考慮基于狀態(tài)反饋的控制器，其形式為

式中，Ki∈Rm×n為控制器增益。

下面先給出系統(tǒng)有限時間有界(FTB)和有限時間鎮(zhèn)定(FTS)的相關(guān)定義。

定義1［19］(有限時間有界)對于給定的有限時間步長 L，系統(tǒng)(1)(μk=0)是關(guān)于(c1，c2，L，d)有限時間有界的，如果滿足條件(3)的擾動dk，下列條件成立：

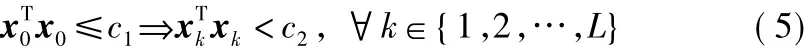
式中，c1＜c2，L為給定的正整數(shù)。

定義2［19］(有限時間鎮(zhèn)定) 設(shè) μk=Kixk，系統(tǒng)(1)關(guān)于(c1，c2，L，d)有限時間鎮(zhèn)定，如果滿足條件(3)的擾動dk，均應(yīng)滿足條件(5)。

引理 1［20］給定兩個反饋矩陣 Ki，F(xiàn)i∈Rm×n，對于 x∈Rn，如果 x∈ψ(Fi)，則

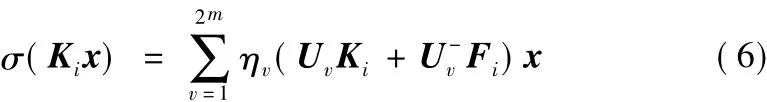
引理 2［21］設(shè) P∈Rm×m為正定對稱陣，矩陣 φi∈

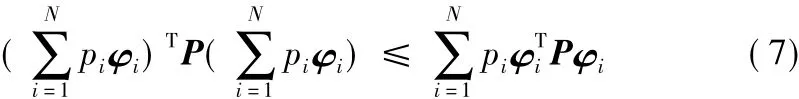
代入控制器(4)，通過引理1對執(zhí)行器飽和進行分解，得到如下閉環(huán)系統(tǒng)：

2 主要結(jié)論

2.1 有限時間鎮(zhèn)定(FTS)分析

定理1 考慮離散閉環(huán)系統(tǒng)(8)是基于(c1，c2，L，d)有限時間鎮(zhèn)定的，如果存在常數(shù)μ≥1，σ1，σ2＞0依賴模態(tài)的正定對稱矩陣Xi∈Rn×n，受限于模態(tài)的矩陣Yi∈Rm×n，正定對稱矩陣 Q∈Rn×n和 Fi∈Rm×n，使得下述條件成立：

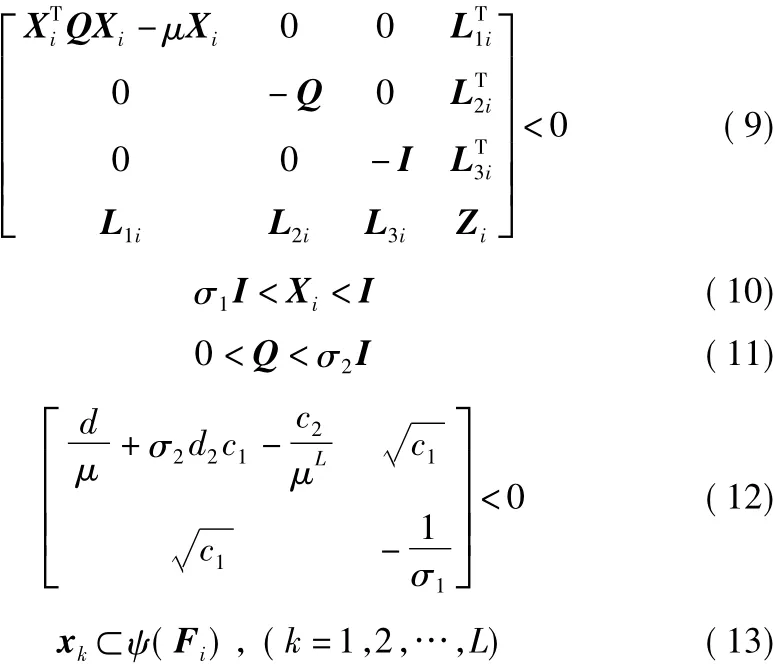
其中：

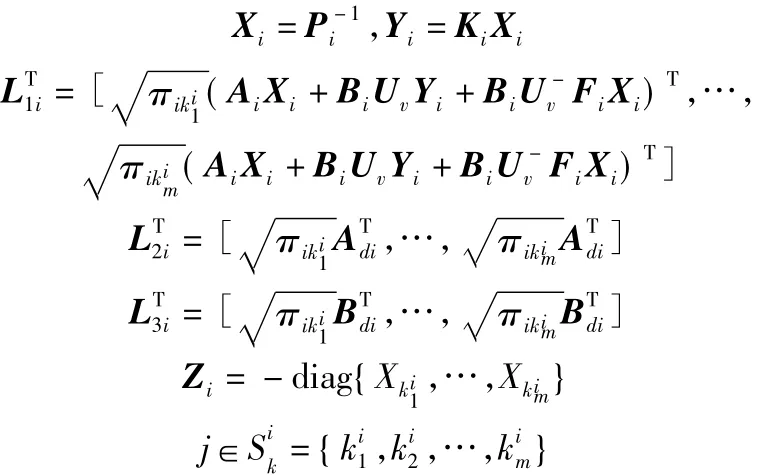
證明 構(gòu)造隨機Markov切換的Lyapunov函數(shù)：

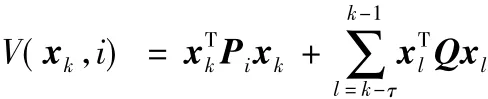
則

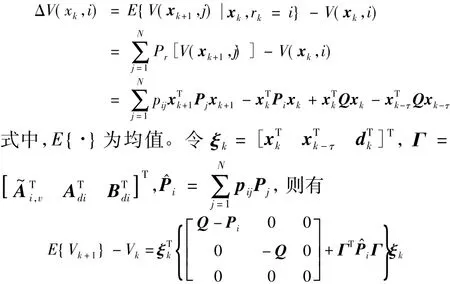
考慮到系統(tǒng)(1)中含部分轉(zhuǎn)移概率未知的情況，根據(jù)轉(zhuǎn)移概率矩陣的相關(guān)性質(zhì)，可以得到如下條件：

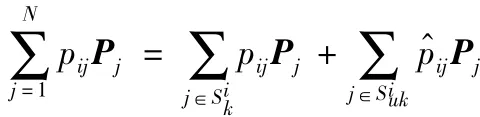
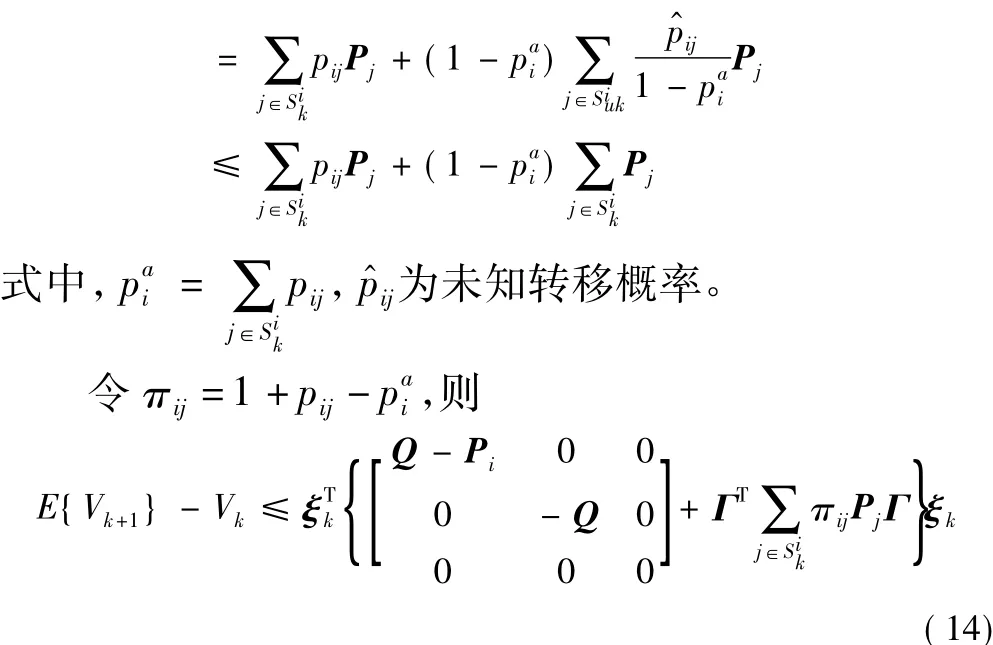
假設(shè)：

根據(jù)不等式(15)，可得如下結(jié)果：

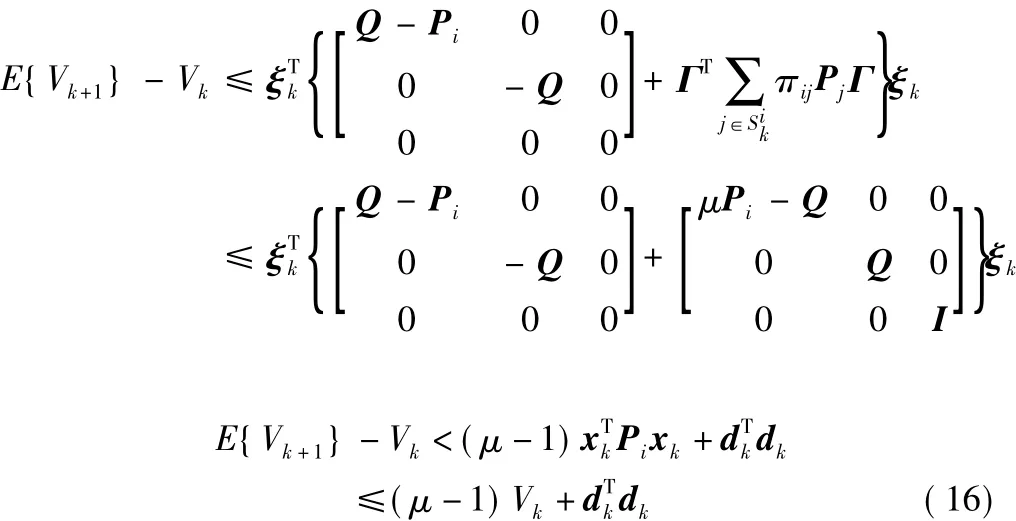
即

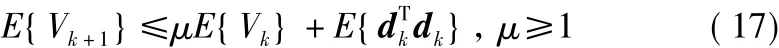
通過矩陣遞推法，可知：

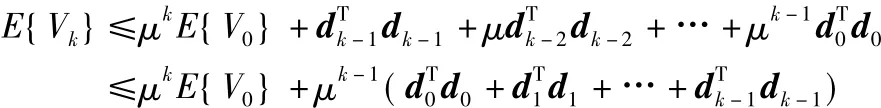
考慮任意的 k∈{1，2，…，L}和條件(3)，下列不等式成立：

由定義1，進一步可得

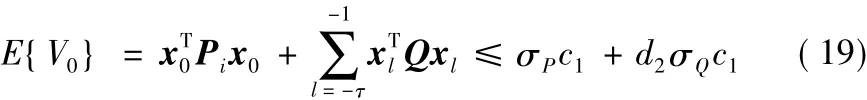
式中，σP=σmax(Pi)，σQ=σmax(Q)，固定時滯滿足0＜τ≤d2。

將不等式(19)代入式(18)，可推導(dǎo)出：

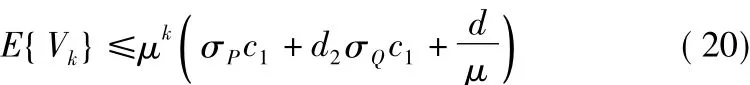
另外，對于任意的i∈S，有

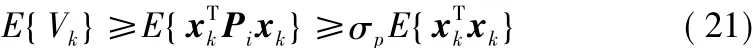
式中，σp=σmin(Pi)。

根據(jù)條件(20)和條件(21)，有

對條件(12)運用舒爾補引理，并根據(jù)條件(10)和條件(11)可得：

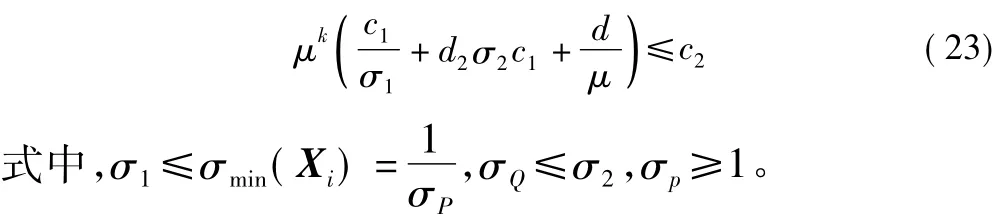
由(22)可推導(dǎo)出：

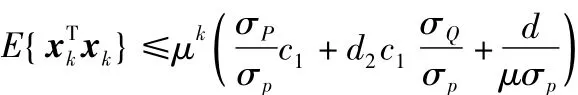
將不等式(23)代入上述不等式中，可得

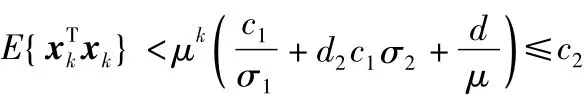
因此，系統(tǒng)狀態(tài)響應(yīng)是有限時間鎮(zhèn)定的。當(dāng)狀態(tài)向量xk滿足條件(13)，保證了反饋控制作用在線性的有界區(qū)域。

證畢。

注記1：下面將證明不等式(15)與條件(9)等價。

首先，令 Ai，v=Ai+BiUvKi+BiU-vFi，應(yīng)用引理2，將式(14)化簡為

由此，將不等式(15)進行展開，可得

對于?v∈{1，2，…，2m}恒成立。

將式(24)兩邊同時左乘，右乘diag{P-1i，I，I}，并取Xi=P-1i，Yi=KiXi，迭代運算即可得證條件(9)。

2.2 狀態(tài)反饋控制器設(shè)計

當(dāng)μ確定時，不等式(9)，式(13)是線性矩陣不等式，可通過LMIs進行求解。將FTS控制器的設(shè)計問題轉(zhuǎn)化為下述優(yōu)化問題：

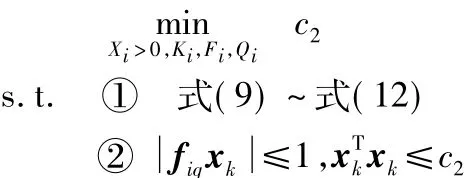
式中，fiq為Fi的第q行。

下面將上述優(yōu)化問題轉(zhuǎn)化為LMIs問題。

令Vi=XTiQXi，Hi=FiXi，并確定 μ 的值，將不等式(9)、式(12)轉(zhuǎn)化為關(guān)于 Hi，Xi，Yi，Vi的線性矩陣不等式。

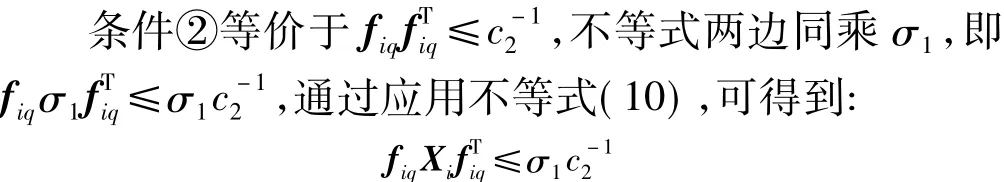
應(yīng)用Schur補引理，可得到

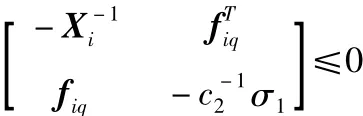
上述不等式同時左乘，右乘diag{Xi，I}，可得

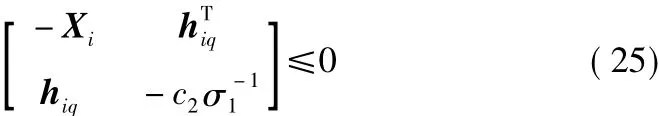
式中，hiq為Hi的第q行。

當(dāng)σ1為固定值時，不等式(25)為線性矩陣不等式。

綜上所述，通過確定 μ，c1，σ1的值，可得到帶LMIs約束的優(yōu)化問題：

注記2：考慮上述優(yōu)化問題有可行解，系統(tǒng)為有限時間鎮(zhèn)定，其控制器為Ki=YiX-1i，且c2越大，有限時間鎮(zhèn)定的可控邊界范圍越大。

3 數(shù)值示例

考慮離散Markov跳變系統(tǒng)(8)具有兩個模態(tài)，參數(shù)為

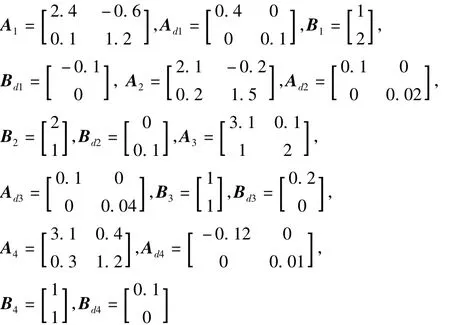
轉(zhuǎn)移概率矩陣如下：

令 c1=8，σ1=0．01，T=50，μ =1。

通過求解LMIs約束的優(yōu)化問題(26)可得(c2)min=17.042，對應(yīng)的FTS控制器為圖3 xTkxk軌跡

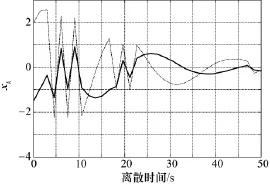
圖2 狀態(tài)軌跡

從圖1～圖3可知所求得的狀態(tài)反饋控制器K1、K2使得初始狀態(tài)為xT0=［-1.5 2］的系統(tǒng)，在反饋控制器的作用下，實現(xiàn)了有限時間鎮(zhèn)定。

4 結(jié)束語

本文研究了含未知但有界擾動，部分轉(zhuǎn)移概率未知和執(zhí)行器飽和的時滯Markov跳變系統(tǒng)的有界時間穩(wěn)定性問題，推導(dǎo)了系統(tǒng)有界時間鎮(zhèn)定的充分條件，并通過將優(yōu)化問題轉(zhuǎn)化為線性矩陣不等式的方法，求解了相應(yīng)狀態(tài)反饋控制器的增益。仿真示例有效表明了該方法設(shè)計的反饋控制器能在滿足既定條件下，實現(xiàn)系統(tǒng)的有限時間穩(wěn)定的指標。