基于模型的PI魯棒控制的電子節氣門方法研究

李學軍，張 生，于皓宇

(1.長春大學電子信息工程學院，吉林長春 130022；2.長春大學研究生院，吉林長春 130022)

據研究表明，汽車發動機的進氣量在一定程度上決定汽車排放空氣污染物的量。研究電子節氣門的控制方法對減少汽車污染物排放，改善汽車動力特性是非常有現實意義的。國內外學者也做了大量研究。

文獻［1］采用前饋線性化與模糊自適應控制相結合的方法，該控制系統穩定性好、精度高。

文獻［2］設計滑模控制器控制電子節氣門，在閉合階段，滑模控制幾乎沒有超調，且能快速準確地跟蹤油門踏板的動作指令。

文獻［3］利用反推法設計了一個非線性的電子節氣門系統的控制規律。

文獻［4］通過ISS相關的穩定性理論證明了控制系統的穩定性和魯棒性，并用快速原型dispace驗證了此方法的有效性。

Vasak等人基于精確的數學模型設計了帶約束時間的最優控制器［5］。該方法與文獻［6］、文獻［7］的控制算法一樣，高度依賴模型的精確度，當模型的參數發生微小攝動時，控制效果會急劇下降。

針對實際控制對象的參數攝動和外界干擾，本文設計了基于模型的電子節氣門PI魯棒控制器，該算法能較好地抑制由于參數攝動和干擾帶來的影響，達到較好的控制效果。

1 電子節氣門建模

1.1 直流電機的數學模型

電子節氣門等效為直流電機，由基爾霍夫定律知電機回路方程和扭矩方程：

式中，Ra為電樞回路的等效電阻(Ω)；ia為流入電機的電流(A)；La為回路的等效電感(H)；kv為電機反電動勢常數(V/(rad·s)-1)；T'm為電機輸出扭矩(N·m)；Tmf為摩擦扭矩(N·m)；Jm為電機的轉動慣量常數(kg·m2)。

忽略電機電感影響，方程(1)簡化為

考慮實際電路中電機的驅動有

式中，u為輸入電機的占空比；Vbat為汽車上的電瓶電壓(V)。

由方程(2)～方程(4)得

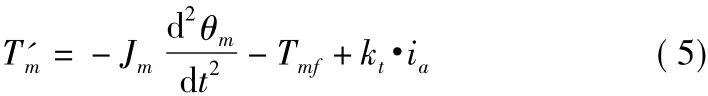
1.2 減速齒輪組的數學模型

減速齒輪組輸入是電機輸出扭矩Tm(N·m)和電機轉角θm(rad)，輸出是減速齒輪組扭矩Tg(N·m)和節氣門轉角θ(rad)(θ=1/n·θm)。忽略齒輪間隙影響，則有

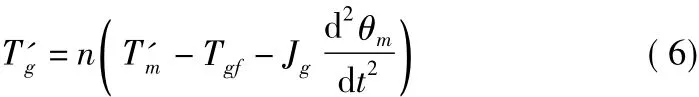
式中，n為從電機與節氣門閥片轉角的比值；Tgf為摩擦而損失的扭矩(N·m)；Jg為齒輪組的轉動慣量(kg·m2)。

1.3 復位彈簧的數學模型

復位彈簧的扭矩特性對其做等效處理得到數學表達式為

式中，kpre為彈簧的預緊力矩系數(N·m)；θ0為節氣門靜態時的開度(rad)；ksa為θ≥θ0時彈簧的彈性系數(N·m/rad)；ksb為 θ0＞θ≥0 時彈簧的彈性系數(N·m/rad)。

1.4 節氣門的數學模型

設節氣門閥片穩定在一定的開度時，電子節氣門達到平衡狀態。因此有

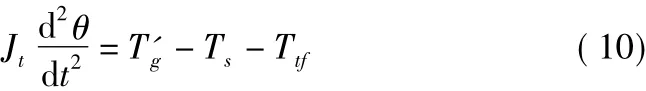
式中，Jt為節氣門體的轉動慣量(kg·m2)；Ttf為節氣門在轉動過程中損失的摩擦扭矩。將式(5)～式(7)代入式(10)，整理得

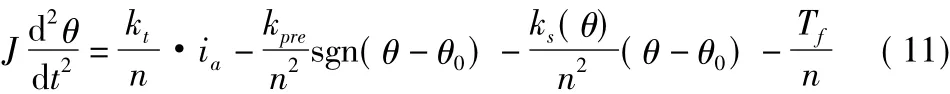
式中，θp=轉換為度數的系數。

參考文獻［8］，將摩擦力分解為庫倫摩擦和滑動摩擦，則有

模型參數如表1所示。

表1 模型參數

2 電子節氣門控制器設計

針對電子節氣門模型，假設xd是需要的理想位置，令e=xd-x1為電子節氣門位置誤差，則速度誤差

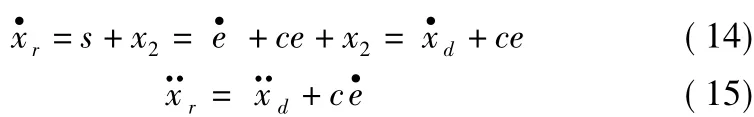
推導出

控制律可以設計成

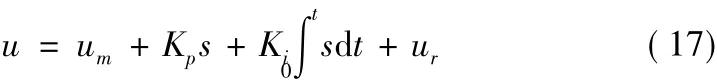
式中，Kp＞0；Ki＞0；um為基于模型的控制量；ur為魯棒項。令

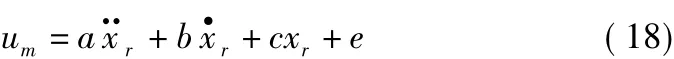
其中，

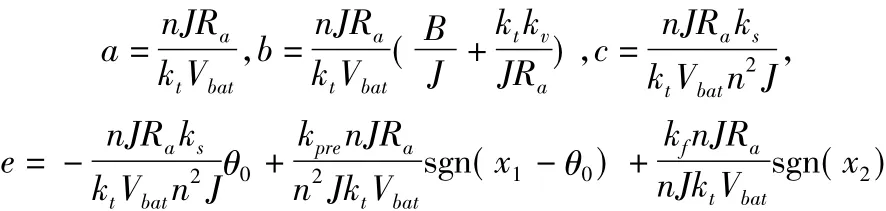
控制項ur=krsgn(ω)就是基于PI的魯棒控制。這項使得節氣門在用PI控制的同時，當節氣門的參數發生變動時，控制器能做出調節來保持控制性能，因而棒項。

基于理想模型得出的控制律在實際系統使用中還需要考慮模型誤差、測量反饋誤差等。在補償了非線性干擾項后，還要使節氣門具有一定的魯棒性。控制項ur=krsgn(ω)就是基于PI的魯棒控制。這項使得節氣門在用PI控制的同時，當節氣門的參數發生變動時，控制器能調節系統保持控制性能，因而具有抗干擾能力。

3 仿真驗證

實際的電子節氣門都存在高頻噪聲，故取高頻干擾量d=10sin(0.02t)，設計的控制器參數為kp=15，ki=0．6，kr=50，Simulink 仿真圖如圖1 所示。

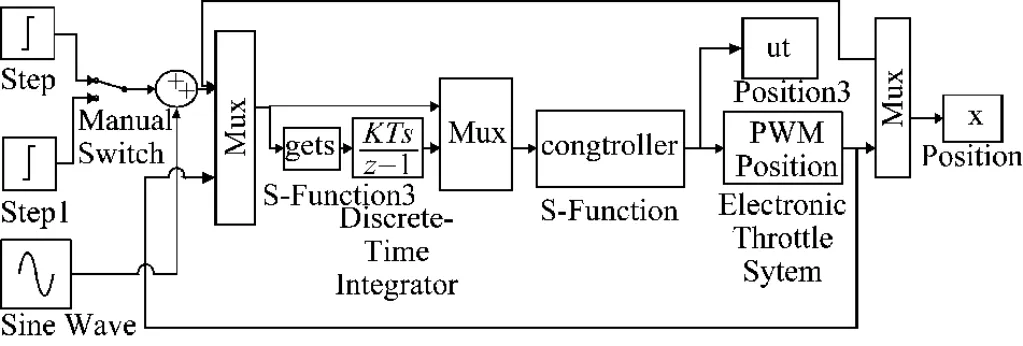
圖1 基于模型的PI魯棒控制仿真

實驗1：設跟蹤目標為10°～80°的大變差階躍信號。仿真結果如圖2所示。由圖2可知，本文算法的魯棒PI控制的平穩特性、跟蹤特性和響應的快速性都較好。基于模型的PI魯棒控制的調節時間為90ms；在階躍變化處幾乎能跟蹤上理想曲線的變化，穩態誤差在±2.5%以內。為說明本文算法的有效性，采用傳統的PI控制器，在相同的P和I參數下出現了振蕩，且超調量比較大。

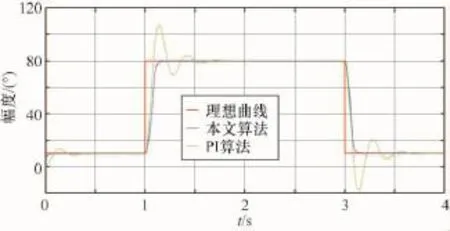
圖2 10°～80°正負階躍響應

實驗2：為了考查系統的角度分辨率，輸入初值為10°，終值為10.2°的小偏差階躍信號。仿真結果如圖3所示。

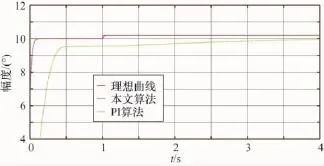
圖3 10°～10.2°的階躍響應

仿真結果可知，本文算法能以較快的速度識別0.2°的角度變化并加以控制。單純的PI控制器雖然能夠識別控制0.2°的角度變化，但是調節時間過長。

實驗3：通常情況下，駕駛員通過油門踏板向控制器輸入頻率在0～3 Hz范圍內，取輸入信號頻率為1.5 Hz和3 Hz的位置跟蹤信號xd=44sin(3πt)+50。仿真的結果如圖4和圖5所示。

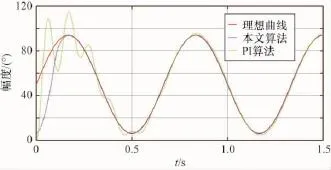
圖4 1.5 Hz正弦響應

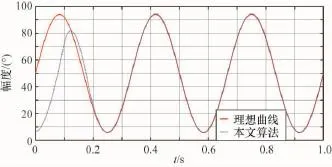
圖5 3 Hz正弦響應

由圖可知總體的控制性能并沒有因為模型的精度誤差而出現較大的差異。主要是基于模型PI魯棒控制對于復雜的非線性采用建模補償的方法得到補償。由于魯棒項的存在，在建模精度不是很高的條件下，也能保證有很好的控制性能。

4 結束語

由于模型補償方法總是存在補償過度和過少的問題，基于力學、物理學等建立的模型參數存在非線性。為了解決此類問題，本文設計了基于模型的PI魯棒控制器，并給出了模型參數。通過搭建基于模型的PI魯棒控制系統進行系統仿真實驗，表明設計的控制系統在減小調節時間，抑制超調量等控制性能方面優于傳統的PI系統，而且系統還具有很好的魯棒性。