基于改進DDPG算法的車輛低速跟馳行為決策研究

羅 穎，秦文虎，翟金鳳

(東南大學儀器科學與工程學院，江蘇南京 210096)

目前，交通擁堵已成為國內各主要城市治理中最棘手的問題之一。據相關統計，每年因交通擁堵給我國造成的經濟損失為1700億左右［1］。高德交通大數據所監測的45個不同規模的城市與地區中，有44座城市的擁堵狀況均處于持續惡化階段［1］，這不僅給居民們的出行帶來了不同程度的困難，也對城市的運轉與建設造成了極大的阻力。同時，道路擁堵也意味著車輛只能低速行駛，并且需要頻繁地啟動、剎車，這會使駕駛員變得疲勞且煩躁易怒，容易出現交通事故；且會大大增加車輛的尾氣排放量，從而降低城市的空氣質量，加劇城市“熱島效應”。

車輛跟馳是車輛行駛過程中最基本的微觀駕駛行為［2］，主要描述的是車輛在單一車道上列隊行駛時，前后兩車間的相互作用［3］，如圖1所示。車輛跟馳行為在無法超車、換道的擁堵環境中是普遍存在的［4］。現如今針對城市交通擁堵環境下的低速跟馳行為研究較少。在這一環境中，車輛時走時停、車距較小、車速較低，所以跟馳行為相對較復雜。然而，對車輛低速跟馳行為的研究有助于解決如今的城市交通擁堵問題，提高擁堵路況下的駕駛安全性并改善駕駛體驗，因此這一研究是十分必要的。

圖1 車輛跟馳駕駛

考慮到傳統的車輛跟馳模型在解決實際道路環境中的行為決策問題時存在自適應能力較低等問題，筆者將采用如今被廣泛關注的深度強化學習(Deep Reinforcement Learning)方法來進行車輛低速跟馳行為決策問題的研究。深度強化學習是強化學習(Reinforcement Learning)與深度學習(Deep Learning)相結合的產物，深度神經網絡使得強化學習方法能夠擴展到以往很難處理的決策問題，即具有高維度狀態空間或連續動作空間的環境［5］。目前，已有研究者將強化學習中的Q-learning算法［6］與深度強化學習中的DQN算法［7］進行改進以應用于智能車輛的自動駕駛控制，但是它們在處理車輛跟馳行為決策這樣的連續動作空間問題時仍有欠缺，因此選擇深度確定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法進行車輛低速跟馳行為決策研究，同時提出了基于屏障控制方法(Control Barrier Functions，CBF)的改進 DDPG算法以優化決策效果。

1 強化學習理論基礎

強化學習的主要特點是試錯與延時回報，其基本結構與流程如圖2所示，智能體(Agent)學習如何在環境中采取動作(離散動作或連續動作)，不需要先驗知識，僅通過不斷的交互試錯、獲得經驗，最終得到最優策略。

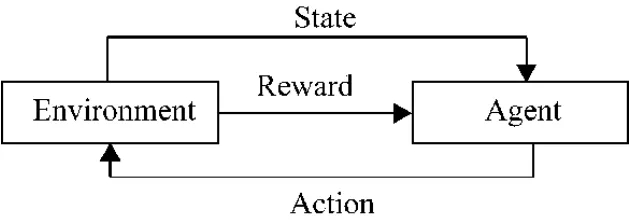
圖2 強化學習基本模型

強化學習主要包括四大要素，分別是狀態、動作、狀態轉移概率以及獎勵值函數，其學習過程主要可用馬爾可夫決策過程(Markov Decision Process，MDP)來描述［8-9］，MDP 由 ＜S，A，P，R ＞ 四元組來刻畫，其中，S={s1，s2，s3，…}表示狀態空間，是所有狀態的有限集合；A={a1，a2，a3，…}表示動作空間，是所有動作的有限集合；P為狀態轉移概率矩陣，Pass1=P［St+1=s1|St=s，At=a］表示在s狀態下采取a動作，轉變為s1狀態的概率；R=r(s，a)為獎勵值函數，表示在s狀態下采取a動作所獲得的獎勵值。智能體在與環境進行交互的過程中，在狀態ST處的累計獎勵為自T時刻起未來執行一系列動作后所能獲得的獎勵值，即T+1，T+2，T+3，…所有時刻的獎勵值之和，表達式為

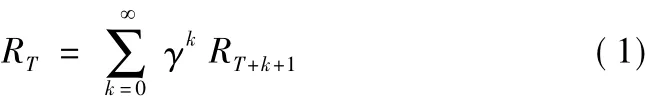
式中，γ為折扣因子，用以權衡當前獎勵與長期獎勵的關系，取值范圍為［0，1］，該值越小，則說明越重視當前獎勵，反之則越重視長期獎勵。

強化學習的最終目的是學習到最優策略π以得到最大的累計獎勵期望，即

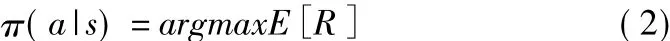
為便于求解該最優策略π，需要對某個狀態與動作的優劣進行評估，因此，引入了狀態值函數與動作值函數的概念，其表達式分別為

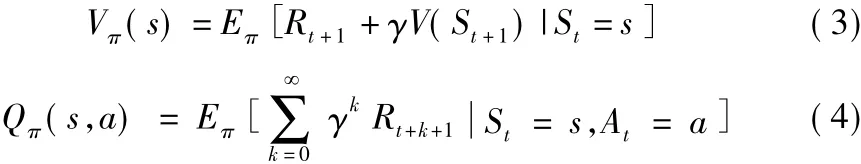
對于以上函數的求解可利用基于表的方法與基于值函數逼近的方法，前者包括動態規劃法、蒙特卡羅方法、時間差分法等，其實質是建立一張行值為狀態、列值為動作的表，通過不斷的循環迭代對表中的值進行更新，在狀態空間比較大時，用這一方法求解非常困難，因此，越來越多的研究開始關注第二種方法，即利用深度神經網絡逼近值函數，由此深度強化學習便應運而生。

Deep Mind于2013年提出的DQN算法是深度強化學習的開山之作，該算法使用卷積神經網絡對Q-learning中的動作值函數進行擬合，同時采用了經驗池機制，通過在經驗池中隨機均勻采樣，模糊了訓練樣本間的相關性；并且，對過去的多個樣本做均值處理，從而平滑訓練樣本的分布［10］。DQN算法及其衍生算法在學習離散動作策略上取得了較為顯著的成果，可是在處理連續動作決策問題方面卻比較困難，雖然也可以把連續動作進行離散化，但離散后膨脹的動作空間容易使算法陷入維數災難。2015年9月，Deep Mind提出了DDPG算法，該算法在確定性策略梯度(Deterministic Policy Gradient，DPG)算法的基礎上發展而來，屬于無模型(Model Free)方法，其核心是Actor-Critic方法［11］。前人的研究表明，DDPG算法在多種連續行為決策問題上表現良好。

2 基于改進DDPG算法的車輛低速跟馳行為決策

2.1 DDPG算法原理

DDPG中建立有Critic網絡和Actor網絡，其結構分別如圖3所示。這兩個網絡間的聯系為：首先環境給出狀態觀測量s，智能體根據Actor網絡做出決策動作a，環境接受此動作后給出獎勵值r與新的狀態s'。此時再根據r更新Critic網絡，然后遵從Critic建議的方向更新Actor網絡。如此循環迭代，直至最終訓練出最優的 Actor網絡［12］。

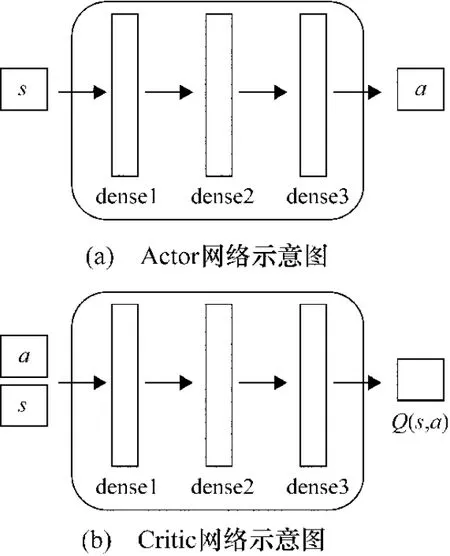
圖3 Actor網絡和Critic網絡示意圖

與DQN相同，DDPG也使用了Target網絡以保證參數收斂。假設Critic網絡為Q(s，a|ω)，其對應的Target-Critic網絡則為 Q(s，a|ω*)；Actor網絡為 π(s|θ)，其對應的 Target-Actor網絡為 π(s|θ*)，其中 ω、ω*、θ、θ*分別為這4 個網絡的參數。

DDPG算法的具體流程如下：

(1)初始化Critic網絡與Actor網絡的參數ω、θ。

(2)將Critic網絡與Actor網絡的參數分別復制給對應的 Target網絡的參數ω*、θ*。

(3)初始化經驗池。

(4)在一個時間步長內進行如下迭代循環。

①初始化Uhlenbeck-Ornstein隨機過程(簡稱UO過程)，目的是引入隨機噪聲。

②Actor網絡根據當前策略π和隨機UO噪聲獲得一個動作at，并將該動作傳達給Agent，at的表達式如下：

③ Agent執行動作at之后，環境返回獎勵值rt及下一時刻的狀態St+1。

④ 將每一次狀態轉換過程(St，at，rt，St+1)都存儲到經驗池中，作為網絡訓練的數據集。

⑤在經驗池中隨機采樣N個狀態轉換過程數據，作為Critic網絡與Actor網絡的一個mini-batch訓練集，其中的單個狀態轉換過程數據可表示為(Si，ai，ri，Si+1)。

⑥計算Critic網絡的梯度：Critic網絡的損失值Loss的計算公式如下，基于標準的反向傳播(Back Propagation)算法，便可以求得Loss相對于ω的梯度?ωLoss。

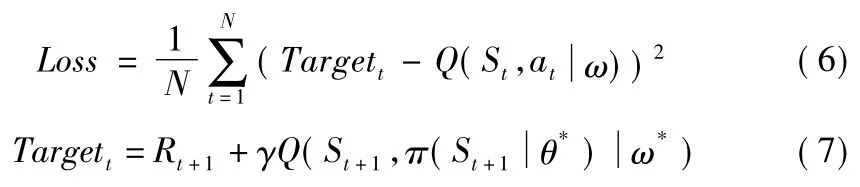
⑦ 更新Critic網絡，采用Adam Optimizer更新ω。

⑧計算Actor網絡的策略梯度，一般根據蒙特卡羅方法使用mini-batch訓練集數據對其期望值進行無偏差估計，具體表達式為

⑨ 更新Actor網絡，采用Adam Optimizer更新θ。

⑩更新Target-Critic網絡與Target-Actor網絡，采用如下公式對ω*、θ*進行更新，式中 τ一般取值為0.001。

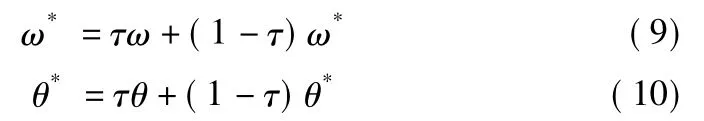
(5)時間步長結束，迭代循環終止。

2.2 高斯過程與獎勵函數設定

在應用DDPG算法以及之后的改進算法實現車輛低速跟馳決策時，將狀態轉換關系做出如下假設：

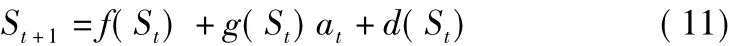
式中，d(St)表示未知的系統動力學部分，用高斯過程(Gaussian Process，GP)模型來對其進行估計，以d^(St)表示。高斯過程是一種非參數回歸方法，在如今的機器學習領域內被廣泛使用，通常用于根據數據估計函數及其不確定性分布的場景中，可視為一個隨機變量的集合，其中的任意有限個樣本的線性組合均服從聯合高斯分布［13］。一個高斯過程可由均值函數μd(s)和協方差函數σ2d(s)來確定，對于過程中任一狀態s*，兩函數表達式分別為

式中，K+σ2noiseIk(si，sj)為高斯過程的核矩陣，k*(s*)=［k(s1，s*)，…，k(sn，s*)］。在算法的決策訓練過程中，智能體對動作的執行則需要通過以上兩式進行高斯過程模型的更新。

同時，將學習過程中的獎勵函數表達式設定為

式中，第1項對加速度進行約束，以優化燃油效率，第2項則鼓勵跟馳車輛盡量保持3 m(不考慮車長)的間距；k表示在模擬的跟馳車隊中選擇第k輛車為A-gent，決策其跟馳行為。考慮到交通擁堵的情況下，本文將安全邊界(Safety Boundary)設置為2 m。

2.3 CBF方法

CBF 方法屬于有模型(Model-based)方法［14］，其關鍵在于通過一個連續可微分的函數H(s)設定了一個安全集合C，可表示為

為了保證學習過程中的絕對安全，智能體的狀態s必須始終保持在安全集合C中，換言之，學習算法應在集合C中進行策略的探索［15］。采用如下表達式描述本算法當中的安全集合：

式中，A表示動作空間；δ表示CBF方法對安全約束的強度，在［0，1］范圍內取值；h(s)則需要在學習過程中不斷進行訓練與更新。

DDPG算法策略試圖產生優化長期獎勵的動作，但執行該動作未必安全，CBF方法作用于DDPG算法執行動作之前，可以視為一個小型控制器，對可能產生危險的動作進行過濾，提供必需的最小干預控制，從而確保整體狀態的安全性。

2.4 DDPG-CBF改進算法

CBF方法與DDPG算法的結合主要分為兩個部分：① 提供補償控制，如圖4(a)所示；② 指導策略探索，如圖4(b)所示。

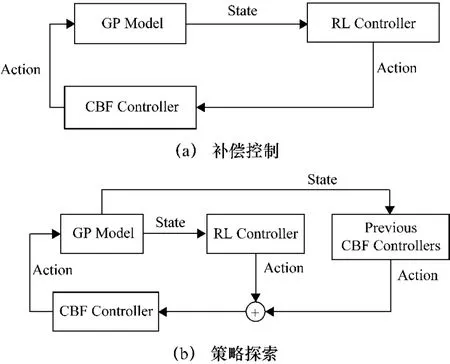
圖4 基于CBF方法的強化學習補償控制和策略探索

算法的初始架構為CBF控制器給DDPG算法提供安全補償，在學習過程中，CBF控制器數據同樣存儲為訓練樣本，以進行CBF安全控制策略的更新，從而對DDPG策略探索提供更有效的指導。DDPG-CBF改進算法的具體流程如下。

(1)初始化DDPG算法策略π0D

DPG，狀態觀測量空間設為D，狀態動作空間設為A。

(2)在t=1，…，T內，進行如下步驟。

②通過CBF控制器得到控制動作u0CBF(St)；

④本次獲得獎勵rt，轉換到下一狀態為St+1，將狀態動作數據(St，u0CBF(St))存儲至A，狀態動作轉換數據(St，u0(St)，St+1，rt)存儲至 D。

(4)更新高斯過程模型與D。

(5)當前迭代過程視為第1次策略迭代，在設定的策略迭代次數內，進行如下循環：

①通過DDPG算法并基于之前的迭代獎勵產生第k次的策略uDkDPG(St)；

③ 在t=1，…，T內，重復步驟(2)，不同的是策略中需加入ubkar(St)分量；

④重復步驟(3)與步驟(4)。

(6)滿足終止條件，迭代結束。

3 仿真實驗結果分析

依靠Tensorflow開源軟件庫完成仿真實驗，同時配置了GeForce GTX TITAN Xp的Cuda環境以提供GPU并行加速運算。實驗中設置了一個含有5輛車的縱向行駛跟馳車隊，通過決策算法控制其中第4輛車的加速與減速，期望目標是避免碰撞，并且保證低速跟馳時的燃油效率最大化(即規避擁堵時過于劇烈的加速度振蕩)。

使用DDPG算法與DDPG-CBF改進算法進行策略學習的過程中最小跟車間距的變化情況以及迭代過程中的累積獎勵對比，分別如圖5、圖6所示。

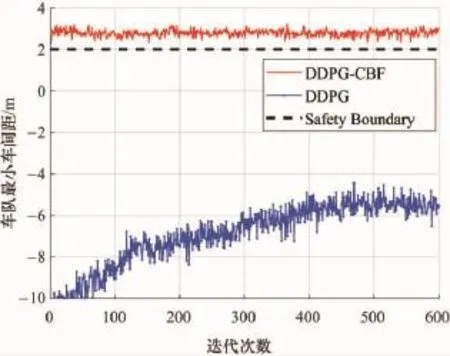
圖5 最小車間距對比圖

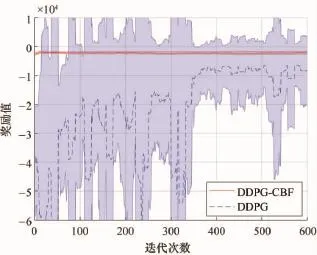
圖6 累積獎勵值對比圖

從圖5可以明顯觀察到，在未結合CBF控制器的情況下，DDPG算法未能在600次迭代內收斂于期望安全策略，即保持3 m的車間距，可見改進前的算法并不能很有效地保障決策的安全性；同時從圖6所示的迭代過程中的獎勵值變化情況來看，DDPG算法在學習過程中獲得獎勵回報較低，并且不確定性與波動性也比較大。而對于DDPG-CBF改進算法而言，不僅能夠使車隊的跟車間距維持在期望車距附近，保證決策的安全性，同時具有很快的學習速度，能夠迅速地獲得較高的獎勵值回報，收斂于最優策略。由此可見，所提出的車輛低速跟馳決策算法的改進效果比較顯著。

4 結束語

本文以獲得有效的車輛低速跟馳策略為研究目標，基于 DDPG算法，并結合 CBF控制器，提出了DDPG-CBF改進算法，實驗證明，該算法在安全保障與學習效率上均體現出了其優越性。但是本文中對跟馳車隊系統的模擬使用的是高斯過程模型，而如何將該算法應用于各種實際的交通仿真場景，并考量駕駛員駕駛習慣差異的影響，可作為后續研究的重點方向。