讓每一次跨越都具有成長的意義

薛正檜

【摘? ?要】“長方形和正方形面積的計算”是一節具有典型意義的“種子課”。通過這節課的教學，可以讓學生產生五大跨越，即從觀察到操作、從直接到間接、從高維到低維、從計量到計算、從歸納到演繹，讓兒童的數學學習像種子的生長一樣充滿生命的意義。

【關鍵詞】長方形;面積;種子課

“長方形和正方形面積的計算”是“圖形與幾何”領域內一節具有典型意義的“種子課”，教學思路總離不開“猜想—驗證—應用”。難道這節種子課只能這樣上嗎？在品讀了老子的《道德經》后，筆者受到了啟發，現以“跨越”為主線，設計并實踐這一課，教學如下。

一、從“觀察”到“操作”的跨越

1.①和②相比，哪一個面積大？你是怎么知道的？

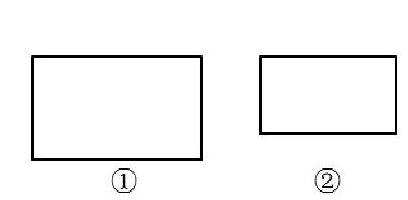
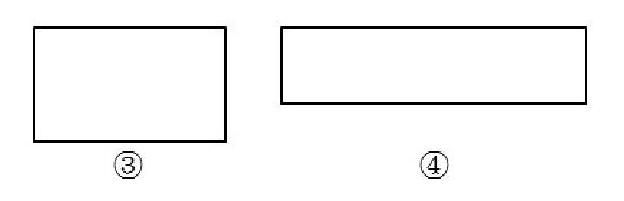
2.③和④相比，哪一個面積大？你能確定嗎？

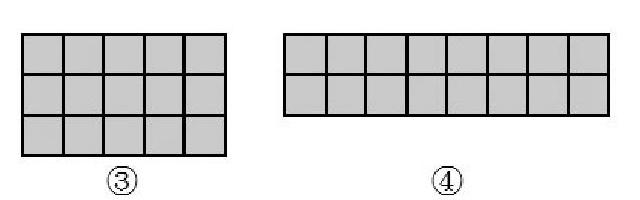
3.有什么好辦法能比較出③和④的大小？

（擺上相同大小的方格）

面積作為一種量，是可以直接計量的，它與長度的計量方法一樣，都是用相應的單位量（1厘米長的線段、1平方厘米大小的正方形等）與測量對象進行比較，從而得到相應的結果。從本質上看，面積計算其實就是單位面積在數量上的累加。比較兩組圖形面積的大小，讓學生體驗到當觀察不能起作用時，直接計量才是確定面積大小的基本方法。學生在認識面積單位時，已經會用1平方厘米的正方形直接測量被測平面圖形的大小，這是一次承前啟后的活動。從觀察到操作，是學生對面積大小由定性把握到定量刻畫的一次飛躍。

二、從“直接”到“間接”的跨越

1.用邊長是1厘米的小正方形計量這些長方形的面積，看誰又對又快。（長和寬都是整厘米數）

2.小正方形不夠了，怎么辦？

3.你最少用幾個小正方形就能量出它的面積？

這里長方形面積的計算體現了操作由直接計量向間接計量的過渡，這個過程對學生理解其他平面圖形的面積計算方法、形成解決有關面積計算問題的一般策略有著十分重要的影響。看誰又對又快，是在速度上提出了要求;小正方形不夠了，是借新問題的刺激“逼迫”學生采用比鋪滿整個長方形更為“經濟”的操作。而最少用幾個小正方形，是引導學生逐步想到“沿相鄰的邊框擺”“內部斜擺”等優化做法，即利用“長邊和寬邊分別能擺幾個”來推測“一共能擺幾個”。從直接到間接，學生的研究方式有了思維的參與。

三、從“高維”到“低維”的跨越

1.你能根據下圖中長度的計量結果，推想出面積的計量情況嗎？（每一小段長度1厘米）

2.只計量長度，你能推算出下面這幾個長方形的面積嗎？

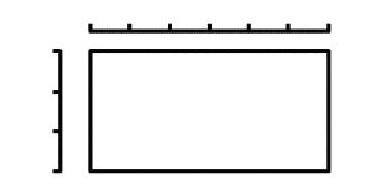
實際解決問題時，人們總是在不斷地求簡、求優。一維的計量是最原始的，二維、三維的計量雖然可以直接計量，但大家通常都是先計量與被測物相關的一維量，然后再利用一定的規則，通過計算得出結果。由此可見，用公式計算面積其實就是在間接計量的基礎上，利用長度來求面積，即計量出長方形的長邊、寬邊分別能擺幾個小正方形，然后相乘。當教師利用推想、計算兩個環節把這一演變過程展示出來以后，學生對算理的理解自然就通了。用單位長度（1厘米、1分米、1米等）來量長方形的長和寬，建構面積計算的模型，是學生原有經驗的提煉、升華。

四、從“計量”到“計算”的跨越

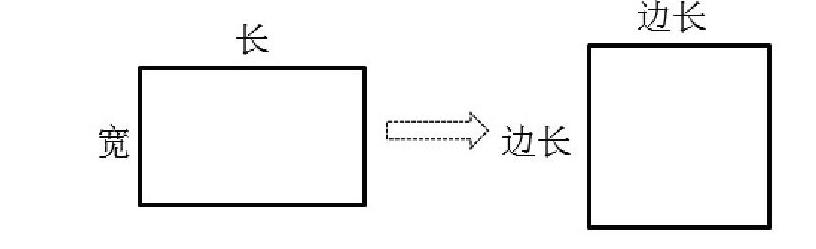
1. 結合下面的圖示，說一說如何計算這個長方形的面積。

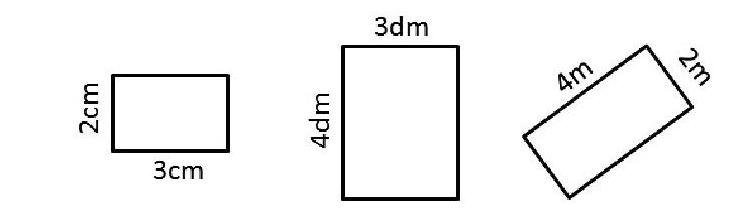
2.長方形的面積怎樣計算？為什么？

與單位長度累加不同的是，單位面積累加后要抽象出相應的公式。理解面積計量的原理，是基于學生已有的測量經驗、推算經驗，引導他們進一步展開深入的思考，確信長方形的面積與它的長、寬存在某種關系，他們完全可以自主推導出公式。長方形的長意味著每排擺幾個，寬意味著擺幾排，面積則意味著一共擺了多少個，所以長方形的面積=長×寬。長方形的面積從計量轉向了計算，操作活動升華到了思維活動。

五、從“歸納”到“演繹”的跨越

1.你會照樣子推導正方形的面積計算公式嗎？（可以結合圖形來說）

2.你能根據長方形的面積公式推導出正方形的面積公式嗎？

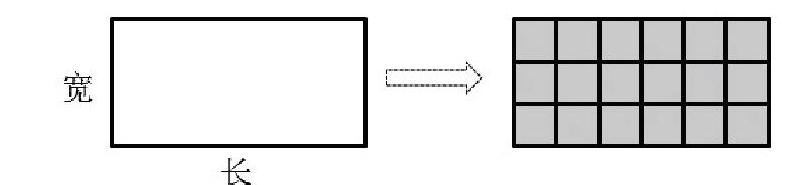
基于兒童的思維習慣擅長于直觀的特點，他們往往從一個個相關的實例中找到規律（不完全歸納），進而獲得結論，但數學更熱衷于用“演繹”（從一般到特殊）獲得結論。小學數學學習既要基于兒童，也要發展兒童，從正方形面積公式的推導來看，可以根據長方形與正方形的屬種關系進行演繹推理。讓學生說一說自己喜歡的方法是對他們思維即時水平的測定，讓學生試著用“正方形是長和寬相等的特殊長方形”來推導是對他們思維發展方向的期待。

“長方形和正方形面積的計算”一課中的五大跨越，讓學生的數學學習像種子的生長一樣充滿了生命的意義。

參考文獻：

[1]俞正強.種子課[M].北京：教育科學出版社，2013.

（浙江省寧波濱海國際合作學校 315830）