學生解決雞兔同籠問題的協變思維

【摘? ?要】協變思維是人們工作、學習以及生活中常用的思維形式，指的是針對兩個或多個協同變化的變量，進行協調或轉化的思維形式。課堂觀察中發現，學生對于雞兔同籠問題的諸多具體做法中，蘊含著協變思維，可以從中挖掘出具有普遍意義的大想法（Big Idea）。這樣的內容對于教師研究學生的思維規律，提升自身的思維水平，提高教學活動的針對性，都有所裨益。

【關鍵詞】協變思維;大想法;雞兔同籠;讀懂學生

如今的課堂教學倡導以學習活動為中心，當學生主動性充分發揮的時候，就會產生諸多教師難以預料的生成。如何面對并應對學生多樣的生成，就成為教師現實的挑戰。一個基本觀點是：向學生學習，讀懂學生做法中隱藏著的想法，將其提升為有價值的課程資源，應用于學生學習活動的設計。

一、協變思維

協變思維也可以叫作協變推理（Covariational Reasoning），指的是針對兩個或多個協同變化的變量，進行協調或轉化的思維形式。[1]比如“人多力量大”這一說法，針對“人數”和“力量”兩個量，認為二者協同變化的規律是“人數越多，力量越大”，是一種“越多—越大（More—More）”的協變思維。

數學學習中，協變思維的應用非常普遍。比如，在問題情境中出現若干只雞，對于雞頭數和雞腳數兩個量，其協變關系可以表述為“雞頭數的2倍等于雞腳數”;同樣，如果有若干只兔，那么兔頭數和兔腳數的協變關系就是“兔頭數的4倍等于兔腳數”。

更為復雜的情況是情境中出現更多的變量。比如雞兔同籠，若干只雞和若干只兔在一起，這時就出現兔頭數、兔腳數、總頭數、總腳數四個變量。某變量的變化或轉換，會引起多個變量的變與不變。如果增加3只雞，那么總頭數增加3，同時總腳數增加6。將1只雞換為1只兔，總頭數不變，總腳數增加2。如果將2只雞換為1只兔，那么總腳數不變，總頭數減少1。

我國小學和初中數學課程中的雞兔同籠問題，是我國歷史上流傳至今的名題。概括地說，解決問題的做法主要是《孫子算經》中的“半足術”，明代《算法統宗》中的“倍頭法”，以及現在初中階段的方程。

如果將雞兔同籠問題敘述為：若干只雞和若干只兔在同一個籠子中，總頭數為35，總腳數為94。求雞和兔各有多少只？

“半足術”做法的第一步是[94÷2=47]，相當于把雞變為“獨腳雞”，兔變為“雙足兔”，使得每只雞的腳數和頭數相同。這樣47-35=12，就得到兔的只數。“倍頭法”做法的第一步是[35×2=70]或[35×4=140]，就是將每只動物的頭數變為2或4，與雞或兔的腳數相同，便于進一步解決問題。[2]

下面介紹三種在四年級和五年級課堂中發現的學生做法，這些做法中蘊含著豐富的與協變思維相關的“大想法（Big Idea）”。

二、盈虧互補

課堂觀察中發現學生的一種做法的第一步是，用總頭數35去平均分配總腳數94（見圖1）。

其中第一步算式為：[94÷35=2……24]，可以理解為，用35個頭平均分配94只腳，也就是如果每只動物2只腳，就會多余24只腳。換言之，如果35只動物都是雞，就多余24只腳。因此需要在總頭數不變的情況下，總腳數增加24。

因為1只雞變為1只兔，頭數不變，腳數增加2。因此圖1做法中的第二步[24÷2=12]，就是將12只雞換為12只兔，使得頭數不變，腳數增加24。因此共有12只兔。第三步[35-12=23]（圖1中學生筆誤：34應為35），求得雞只數為23。類似于此的做法還有寫為分數形式（見圖2）。

這種做法背后隱藏的想法，既不同于《孫子算經》中的半足術，也不同于《算法統宗》中的倍頭法。半足術與倍頭法都是意圖將動物的頭數與腳數變為相同，也就是“變異為同”。而學生這樣的做法首先是“平均分配”，分配之后，再對剩余部分進行調整。其中調整的過程所運用的，就是協調雞只數與兔只數相互轉換中變與不變的協變思維。

協調變量協變過程中的變與不變，也可以叫作“盈虧互補（Compensation）”，是一種應用廣泛、具有一般意義的思維形式。比如下面的幾何問題：

圖3的大正方形內部有三個形狀、大小完全一樣而顏色不同的小正方形，露在外面部分的面積如圖所示。求大正方形的面積。

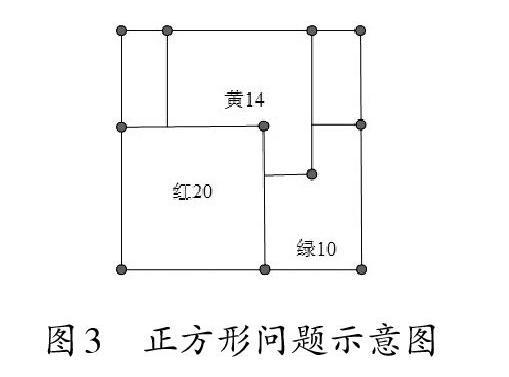
初看題目，似乎無從下手。可以運用協變思維，將黃色正方形向左側平移，移動過程中，黃色正方形露出面積越來越小，而綠色正方形露出面積越來越大，減少部分與增加部分保持相等，二者盈虧互補。移到盡頭后成為圖4形狀。

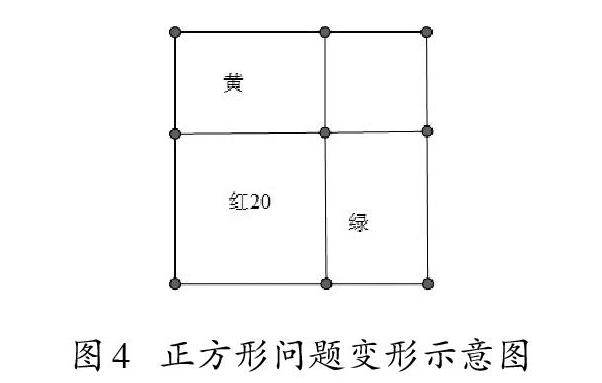
這時黃色和綠色兩個正方形露出面積相等，由于移動過程中兩個正方形露出部分面積相互之間盈虧互補，其總和是不變的。所以圖4中黃色和綠色正方形露出部分面積均為[（14+10）÷2=12]。在此基礎上，問題就不難解決了。

像這樣從解題的具體做法中提取出具有一般意義的想法，西方文獻中通常叫作“大想法（Big Idea）”。大想法的一個特征就是可遷移，可以應用于更廣泛的其他問題。

三、配對分組

課堂觀察中發現的第二種做法是將1只雞和1只兔綁定為一組，使得每一組中包含1只雞和1只兔，因此頭數為2，腳數為6（見圖5）。

第一步[94÷6=15……4]，是用總腳數94除以每組腳數6，說明一共有15組，多余4只腳。也就是如果雞和兔各有15只，這時就會多出4只腳。

第二步[4÷2=2]，是將剩余的4只腳分配給2只雞，此時就有15只兔、17只雞，總頭數是30+2=32。

第三步[35-（30+2）=3]，表明總頭數少了3。如果用1只兔換為2只雞，能夠使得頭數增加1，腳數不變。

第四步15-3=12和第五步[3×2+15+2=23]，就是將15只兔中的3只，變為[3×2=6]只雞。因此得到兔有12只，雞有23只。圖5最后一步23+12=35，是對結果的檢驗。

這一做法運用配對分組（Grouping）的想法，將1只雞和1只兔視為一個整體，而后再對剩余部分進行調整，調整的過程同樣用到盈虧互補的大想法。

配對分組不僅是一種解決問題的做法，也是可以遷移到其他問題，具有一般意義的大想法。比如下面著名的“百僧問題”。

100個和尚吃100個饅頭，大和尚1人吃3個，小和尚3人吃1個。問大和尚和小和尚各有多少人？

運用分組的想法，將1個大和尚和3個小和尚視為一組，這樣每一組中大和尚1人，小和尚3人，一共4人，吃饅頭4個。這樣就將100個和尚和100個饅頭分為25組。因此得到答案：大和尚25人，小和尚75人。

配對分組作為一種思維形式，實質是將不同對象關聯起來，視為整體。運用不同對象之間的異同、因果關系進行思考。比如美國20世紀著名的數學科普作家馬丁·加德納（Martin Gardner ： 1914-2010），曾經發表過一個命名為“Corner to Corner（點對點）”的幾何問題。

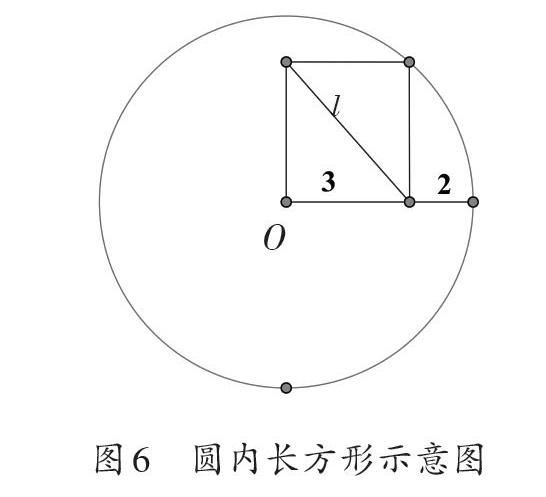
圓內一個長方形，求長方形對角線l的長度。[3]

如果眼睛只盯著圖中對角線l，就無法將其與已知數據3和2建立聯系。運用配對的想法，長方形有兩條對角線，而且長度相等，可以發現另外一條對角線其實就是圓的半徑，因此立刻知道對角線l的長度其實就是圓的半徑長度：3+2=5。

四、先取半，再調整

觀察中還發現，有學生做法的第一步是用總頭數35除以2（見圖7），相當于先假定雞只數為17，兔只數為18;或者反過來雞只數為18，兔只數為17。

這樣的做法可以概括為“先取半，再調整”。同樣運用了雞和兔相互轉換的協變思維。如果雞只數是17，兔只數為18，那么總腳數為[17×2+18×4=106]，比實際總腳數多了106-94=12。只需要將6只兔換為6只雞，使得總頭數不變，總腳數減少12。因此雞只數為17+6=23，兔只數為18-6=12。這種“先取半，再調整”的做法也蘊含著可遷移、具有一般意義的大想法。比如下面的“和差問題”。

全班共有35名學生，男生比女生多3人。男、女生各有多少人？

通常的做法是通過“和加差”或者“和減差”解決問題。如果按照“先取半，再調整”的想法，第一步可以先將全班35人取半，具體做法為：[35÷2=17.5]。相當于假定男女學生各有17.5人。這種不符合實際的情境并不真實，因為不可能出現“0.5人”的情況。

心理學中有一個叫作“意象（Mental Imagery）”的概念，指的是“心眼所見（Seeing in the minds eye）”的情境[4]，這樣的情境往往有悖于親眼所見的“真相”。在和差問題的思考過程中，“0.5人”的意象，作為思考過程中的一個環節，雖然違背真實，但對于問題解決的思考仍然是有效的。

接下來，將意象中的“17.5個女生”中的“1.5個女生”改變為“1.5個男生”，這時總人數守恒不變，男生人數增加為17.5+1.5=19（人），女生人數減少為17.5-1.5=16（人），符合題目中男生比女生多3人的要求，也就得到了問題的答案。

“取半（Halving）”作為一種分配活動中的大觀念，其應用十分廣泛。《孫子算經》中對雞兔同籠問題解決所采用的半足術，就是對總腳數94取半。與其相關的大想法還有“加倍（Doubling）”和“等分（Equivalence Grouping）”等，比如《算法統宗》中的“倍頭法”就用到了“加倍”。前面談及的“配對分組”實際上也是等分想法的體現。

日常的數學教學中，解題是必不可少的教學活動，教師多多留意并積累學生異樣的做法，從中挖掘具有一般意義的大想法，將之應用于其他問題的解決，應當成為教師自身專業發展的有效途徑。

如今的數學教學倡導“變教為學”，期望以教師“講為主”的教學，改變為以學生“學為主”的教學。對于教師的一個挑戰是如何面對學生不同于預設的生成。這樣的生成可能是正確的，可能是錯誤的，也可能是合理但不完善的。所有應對策略的前提是：耐心地聽，努力地讀，廣泛地用。

參考文獻：

[1]Marilyn Carlson， Sally Jacobs， Edward Coe， Sean Larsen and Eric Hsu. Applying Covariational Reasoning While Modeling Dynamic Events： A Framework and a Study[J]. Journal for Research in Mathematics Education，2002，33（5）：352-378.

[2]郜舒竹. 雞兔同籠問題中的辯證思維[J]. 課程·教材·教法，2019，39（9），95-100.

[3]Martin Gardner. Entertaining Mathematical Puzzles[M]. New York： Dover Publications， INC， 1986： 37.

[4] Nigel J.T. Thomas. Mental Imagery[EB/OL]. （2014-09-12）[2019-8-26]https：//plato.stanford.edu/index.html.

（首都師范大學初等教育學院? ?100048）