月牙定理背后的千年傳奇
——從一道高考題說開去

韋 磊

在2018年高考數學全國卷中，有這么一道題，骨骼清奇：

【原題】下面是來自古希臘數學家希波克拉底的幾何圖形，此圖由三個半圓構成.三個半圓的直徑分別是直角三角形ABC的三邊AB，AC，BC，三角形ABC圍成的區域記為Ⅰ，斜線陰影部分的區域記為Ⅱ，白色部分記為Ⅲ，在整個圖形中任取一點，此點取自各部分的概率分別為P1，P2，P3，則（ ）

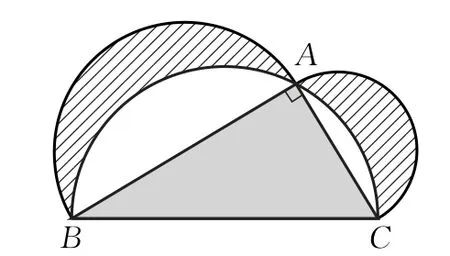
圖1

A.P1＝P2B.P1＝P3

C.P2＝P3D.P1＝P2＋P3

此題難度倒是不大，通過簡單的勾股定理即可得.

設白色部分面積為S1，

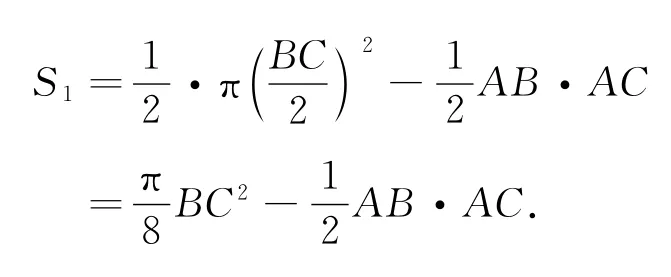
直角邊上的兩個半圓面積為：

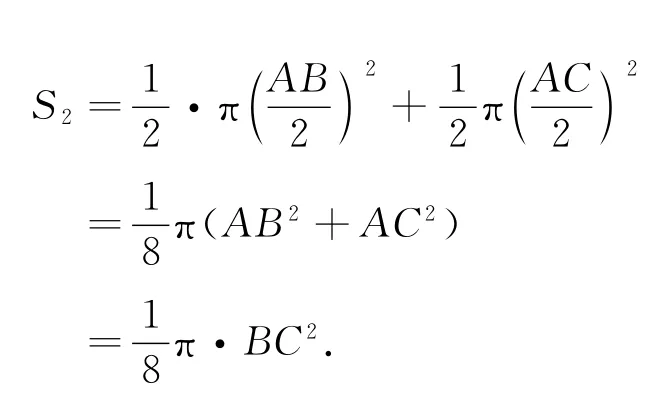
這顯然同直角三角形的面積相同.所以答案是A.

當然清奇之處倒不是此題的難度，而是它不凡的背景.

這個故事，說起來真的是蕩氣回腸.這個故事，就是著名的化圓為方.

注：“化圓為方”是古希臘數學尺規作圖領域中的命題，它與“三等分角”“倍立方問題”并列為尺規作圖三大難題.

一、數與形的競爭，形的勝出

古人從現實生活中逐漸提煉出基本的數學概念，并且這些概念結論什么的逐漸分成兩大陣營——幾何與算術.這兩門學科不像現在那般相互促進，而是在相互競爭——誰管用就信誰.當幾何中有了新的發現，幾何便占據優勢，算術漸被多數人忽視；而當算術有了新的發現，算術又取代幾何的位置成為主流.

畢達哥拉斯學派大概是以著名的畢達哥拉斯定理（也就是勾股定理）而讓我們熟知.實際上這只是畢氏學派在幾何中的一大貢獻而已，他們在算術中的思想往往被我們忽視——大概是這種思想被證明是一種荒謬之故——“萬物皆數”.

這種思想認為，所有的數都能用兩個整數的比值來表示，換成我們今天的話說，那就是所有的數都是有理數.這在我們現在看來顯然是荒謬的，不過在那時，這條原則被奉為圭臬，成為畢達哥拉斯學派的核心教義.這里用教義一詞，并非誤用，因為從很多方面看，畢達哥拉斯學派都不像我們印象之中的學術團體，而更像一個宗教團體.

我們提起這種思想是想讓大家知道，畢氏學派一開始是在幾何與算術兩大陣營都有建樹的，并無偏頗一方之意.但“成也蕭何，敗也蕭何”，畢氏學派因該定理流傳千古，也因該定理毀了自己的思想根基——正是因為畢達哥拉斯定理導致了“無理數”的發現.因為他們發現，直角邊都為1的直角三角形的斜邊，沒辦法用兩個整數的比值來表示.這對畢氏學派來說是災難性的，對人類來說卻是一大喜事.

發現這一現象的，正是畢氏學派的弟子.據說，他因此付出了生命的代價，怒不可遏的其他弟子將其沉入海中.雖然這一點沒有得到證實，但這反映出了畢氏學派的宗教性質——不愿意接受異見.

然而不可公度數的發現，并沒有引導人們去進一步研究數的性質，反倒讓人們對算術失去了信心，就從這個節骨眼開始，幾何對算術的優勢一直支配著希臘，足有一千多年.

二、對面積的癡迷，對美和秩序的追求

古希臘人被幾何的對稱性、視覺美和微妙的邏輯結構吸引住了，尤其是化繁為簡的處理方式，即以簡單和基本的東西作為復雜和紛繁問題的處理基礎.

如果要從大自然中直觀體驗到一兩種幾何體，那么最常見的莫過于直線和圓了.對直線和圓的癡迷，使得直尺和圓規成為了幾何作圖的核心工具（至少在古希臘是如此），而直尺和圓規的實用性反過來增進了直線和圓在古希臘幾何學中的地位.

出于對幾何中美和對稱性的追求，古希臘人開始研究起面積，其本意我猜測是想把描述平面圖大小的量轉化成簡單的正方形.面對著一般圖形求面積的困難，古希臘人心中就萌發“用一個正方形面積取代一個平面圖形的面積”的想法.因為如果能實現，那么規則對稱的正方形替換了不規則不對稱的平面圖形，這是一種以對稱取代不對稱，以完美取代不完美，以有理性取代無理性的過程，也是宇宙所固有的簡約和美的象征.

為了更徹底地反映這種科學精神，古希臘數學家們還對圓規和直尺的用途加以限制：圓規只能畫圓，而直尺，是沒有刻度的直尺，只能畫直線.

三、直邊圖形的遺憾，月牙定理的“曙光”

憑著古希臘人的才華，人們已經能僅憑“尺規作圖”，用正方形的面積表示任何“直邊圖形”的面積，但曲邊圖形卻遇到了困難.人們起初懷疑這種方案的可行性，因為直覺認為尺規不能將曲邊拉直.然而希波克拉底帶著他的月牙定理，讓眾人看到了“化曲為直”的希望.如下圖所示：

以直角三角形三邊為直徑作半圓，兩兩相交成圖中所示兩個陰影月牙形，則兩個陰影月牙形面積之和等于直角三角形面積.

如圖2，S1＋S2＝S△ABC.

圖2

該定理一面世便引起軒然大波，太提神了！一個曲邊圖形的面積就這樣等于了一個直邊圖形的面積，這對于那些一心想尋找化曲為直的數學家來說實在是太振奮人心了.有傳言稱希波克拉底個人都據此宣稱他已經解決化圓為方問題，在后來的辛普利西烏斯的轉述中提到所謂的“化圓為方”問題解決辦法.后來證實這是錯誤的——作者錯誤地將此月牙推廣到任意月牙：

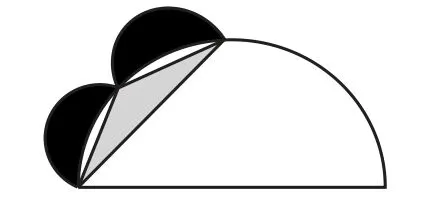
圖3

如圖3所示，作者認為黑色部分和灰色部分面積相同.這顯然只是很不負責任的推廣，稍加計算便可得知其錯誤.實際上直到20世紀，數學家們才證明僅存在五種月牙形能用正方形來表示面積.當然這是后話，不管是非如何，月牙定理確實激起了大家對“化圓為方”問題的興趣，而且他們如此著迷，一做就是兩千多年……

四、千年后的終結

兩千多年來，盡管無數的數學家為幾大幾何作圖問題費盡心思卻仍未有任何突破，但人們始終相信，這些都只是數學家們的能力不夠而已.直到1882年，德國的費迪南德·林德曼證明了該問題的不可能性——根本原因就在于圓周率π的超越性，這個問題才算得到了圓滿的解決.

所謂超越數，這是一個比較復雜的概念，你可以理解成比一般的無理數更為“無理”的無理數.

數學家證明，只要是超越數，僅僅使用我們的尺規，是沒辦法做出來的.而我們的“化圓為方”，實際上就是做出長為的線段，由于π的超越性，這是沒辦法做出來的，也就證明了“化圓為方”是不可能的.

但若是沒有尺規的這個限制，“化圓為方”之類的問題還是很容易解決的.比如說：將圓滾一圈就滾成直線，然后再對直線四等分就行了.

回顧整個歷史的發展過程，當人們最初提到用尺規化圓為方時，人們直覺認為這是不可能的，但是月牙定理顛覆了直覺；而后，林德曼等人的否定結論表示，直覺并非都錯——對于“化圓為方”問題來說，直覺永遠都是對的.

更有戲劇性的是，當初是因為不可公度數的出現，使得人們認為代數不可靠，轉而去研究幾何；而幾何上的問題最終卻成為了代數問題.什么叫數形結合？這就是.

順便提一句，關于無理數的困擾之類，在我們中國人這里從來都不是問題，雖然我們早已發現勾股定理.倒不是我們比別人領先，而是我們壓根就沒有意識到這是一個問題.我們的數學大多是作為算術之用，我們可以取到根號2的任意精確的值，至于他最終是什么，我們沒有關心過.

歷經千年，只為證明人們的直覺.當然，歷經千年的洗禮，雖然最終回歸到了直覺，但我們的思維，早已超越.