基于度量角度整體把握數(shù)的運(yùn)算教學(xué)

董文彬

摘? ?要：文章嘗試跳出教材的編排順序，將小學(xué)數(shù)學(xué)中的運(yùn)算、度量?jī)纱蠛诵膬?nèi)容聯(lián)系起來(lái)，在厘清認(rèn)識(shí)的前提下，基于對(duì)“單位”的認(rèn)識(shí)，系統(tǒng)論述了小學(xué)階段數(shù)學(xué)學(xué)習(xí)中如何從度量的角度整體把握數(shù)的運(yùn)算教學(xué)，闡明度量的基本思想在數(shù)的運(yùn)算教學(xué)中的價(jià)值體現(xiàn)，以及對(duì)實(shí)際教學(xué)的思考與啟示，以期能夠從整體上理解數(shù)學(xué)課程理念、掌握數(shù)學(xué)課程目標(biāo)、認(rèn)識(shí)數(shù)學(xué)課程內(nèi)容、設(shè)計(jì)教學(xué)內(nèi)容主線，最終幫助教師從整體上把握小學(xué)數(shù)學(xué)課程教學(xué)。

關(guān)鍵詞：度量;數(shù)的運(yùn)算;單位運(yùn)作;整體把握;教學(xué)研究

中圖分類號(hào)：G623.5? ? ? 文獻(xiàn)標(biāo)識(shí)碼：A? ? ? 文章編號(hào)：1671-0568（2019）22-0014-04

在小學(xué)數(shù)學(xué)課程中，有些學(xué)習(xí)內(nèi)容因?yàn)槌休d著數(shù)學(xué)中永恒不變的核心本質(zhì)思想而一直備受關(guān)注，比如運(yùn)算、度量等。但長(zhǎng)期以來(lái)，不少教師因?yàn)閼T性的思維認(rèn)知將這些核心內(nèi)容的教學(xué)割裂開(kāi)來(lái)，認(rèn)為運(yùn)算就是運(yùn)算，更多的是“數(shù)與代數(shù)”領(lǐng)域的內(nèi)容，度量就是度量，更多的是“圖形與幾何”領(lǐng)域的內(nèi)容。其實(shí)，這些看似“天各一方”的核心內(nèi)容之間是有天然聯(lián)系的，有時(shí)我們要跳出教材的編排順序，跳出教與學(xué)的方式，去思考這些核心內(nèi)容之間存在的本質(zhì)聯(lián)系，打通這些相通的必然的聯(lián)系，才能從整體上理解數(shù)學(xué)課程理念、掌握數(shù)學(xué)課程目標(biāo)、認(rèn)識(shí)數(shù)學(xué)課程內(nèi)容、設(shè)計(jì)教學(xué)內(nèi)容主線，最終從整體上把握小學(xué)數(shù)學(xué)課程教學(xué)。

一、厘清認(rèn)識(shí)

在從度量的視角整體審視運(yùn)算教學(xué)的前期，我們主要思考以下兩個(gè)問(wèn)題：

1. 什么是度量？一提到“度量”，我們立刻會(huì)想到有關(guān)它的很多核心本質(zhì)與永恒不變的東西，如兩個(gè)核心要素（度量單位、單位的個(gè)數(shù)即度量值）、三條基本性質(zhì)（運(yùn)動(dòng)不變性、合同性、有限可加性）、度量的本質(zhì)是比，等等。度量總體上分為可直接度量和不可直接度量?jī)刹糠郑芍苯佣攘堪ぞ叨攘俊⒐蕉攘亢娃D(zhuǎn)化度量。貨幣單位、質(zhì)量單位、時(shí)間單位、長(zhǎng)度單位、面積單位和體積單位等這些基本的度量單位的認(rèn)識(shí)和建立可通過(guò)工具度量，角度、周長(zhǎng)、面積和體積等這些度量值的獲取可通過(guò)公式計(jì)算來(lái)度量，這是度量教學(xué)的核心部分，多集中在“圖形與幾何”“數(shù)與代數(shù)”兩個(gè)領(lǐng)域內(nèi)（主要在前者）。有一些度量則不能通過(guò)工具或公式計(jì)算獲取，而需把不規(guī)則的物體轉(zhuǎn)化為規(guī)則的物體來(lái)度量，如用“水測(cè)法”度量一個(gè)土豆的體積，在等量替換中保證兩個(gè)量的守恒，這樣的度量我們可稱之為轉(zhuǎn)化度量，因一般通過(guò)實(shí)驗(yàn)進(jìn)行，暫可納入“綜合與實(shí)踐”領(lǐng)域。而有一些量是不可直接度量的，需要通過(guò)兩個(gè)可以直接度量的量的比值來(lái)間接運(yùn)作刻畫(huà)，比如速度可通過(guò)路程與時(shí)間的比值來(lái)刻畫(huà)，密度可通過(guò)質(zhì)量與體積的比值來(lái)刻畫(huà)等。

2. 度量與運(yùn)算教學(xué)共通的核心主線是什么？吳正憲老師說(shuō)過(guò)，小學(xué)數(shù)學(xué)中關(guān)于“單位”這件事無(wú)論怎么重視都不為過(guò)。度量?jī)?nèi)容的教學(xué)深刻體現(xiàn)了這一點(diǎn)，度量教學(xué)的核心是讓學(xué)生經(jīng)歷單位的產(chǎn)生和發(fā)展過(guò)程、單位的累加過(guò)程（數(shù)出度量單位的個(gè)數(shù)），建立和形成單位的觀念，積累度量的學(xué)習(xí)活動(dòng)經(jīng)驗(yàn)。而在數(shù)與運(yùn)算教學(xué)中，建立計(jì)數(shù)單位的概念，感悟數(shù)及數(shù)的運(yùn)算就是單位個(gè)數(shù)的運(yùn)作變換過(guò)程（累加或遞減）是教學(xué)的關(guān)鍵。由此可見(jiàn)，無(wú)論是度量教學(xué)還是運(yùn)算教學(xué)，其核心的東西都是“單位”，其本質(zhì)都是“單位的運(yùn)作和轉(zhuǎn)換”，度量中的實(shí)際量（包含生活中的量、物理量、幾何量）的單位，運(yùn)算中的計(jì)數(shù)單位，“單位”成為核心詞貫穿于這兩大核心內(nèi)容教學(xué)的主線。如此，我們能否從度量的角度來(lái)幫助學(xué)生認(rèn)識(shí)數(shù)與運(yùn)算呢？能否從度量方面幫助學(xué)生體會(huì)“單位化”的思想，進(jìn)一步理解數(shù)的運(yùn)算的核心本質(zhì)呢？

二、度量的基本思想在數(shù)的運(yùn)算教學(xué)中的價(jià)值體現(xiàn)

數(shù)的運(yùn)算主要是指加、減、乘、除四個(gè)維度的數(shù)學(xué)運(yùn)算，同時(shí)又可劃分為整數(shù)、小數(shù)和分?jǐn)?shù)三種不同數(shù)類的運(yùn)算。那么，度量的思想在數(shù)的運(yùn)算中是如何體現(xiàn)的呢？

1. 從度量的角度認(rèn)識(shí)加減法。

（1）整數(shù)加減法運(yùn)算。如“8+6”，如圖1所示，在這條簡(jiǎn)單的數(shù)尺上，數(shù)與格（點(diǎn)）一一對(duì)應(yīng)，往右表示累加，得到“8+6”唯一結(jié)果的操作就是基于這種“一一對(duì)應(yīng)”，數(shù)出計(jì)數(shù)單位的過(guò)程，從8開(kāi)始，以“1”為單位，連續(xù)累加6次，就得到14這個(gè)結(jié)果。這個(gè)運(yùn)算的過(guò)程就是度量單位（計(jì)數(shù)單位）累加的過(guò)程。同樣，運(yùn)算“8+6”，如圖2，10格為1檔，從8開(kāi)始，以“1”為單位，先累加2次到“10”，遇“10”停頓，再累加4次，進(jìn)入下一檔，孕伏“滿十進(jìn)一”，產(chǎn)生新的度量單位（計(jì)數(shù)單位）“十”。

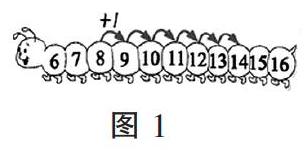
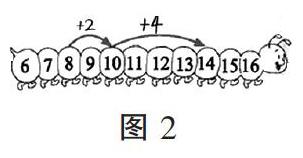
照此，借助于數(shù)軸并沿著數(shù)軸往右，可以1個(gè)1個(gè)地?cái)?shù)，也可以10個(gè)10個(gè)地?cái)?shù)，還可以100個(gè)100個(gè)地?cái)?shù)……在這樣不斷地以計(jì)數(shù)單位累加中，就會(huì)產(chǎn)生“一”“十”“百”……更大的新的計(jì)數(shù)單位，在度量單位的不斷累加運(yùn)算中，方便和滿足了數(shù)量級(jí)擴(kuò)展后大數(shù)加減法的開(kāi)展。

因?yàn)闇p法與加法是互為逆運(yùn)算的關(guān)系，因此從度量的角度認(rèn)識(shí)減法就不難理解。如“239-118”，如圖3所示，在這條數(shù)線上，往左表示“遞減”，從239開(kāi)始，先以“百”為單位遞減1次，再以“十”為單位遞減1次，再以“一”為單位遞減8次，即得到“239-118”的結(jié)果（度量值）121。在運(yùn)算的過(guò)程中，先減幾個(gè)百，再減幾個(gè)十、幾個(gè)一，這正是一種度量思想的體現(xiàn)，從計(jì)數(shù)單位運(yùn)作變換的角度幫助學(xué)生直觀理解數(shù)的內(nèi)部結(jié)構(gòu)，進(jìn)而理解運(yùn)算的意義。

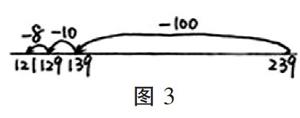
（2）小數(shù)加減法運(yùn)算。由于小數(shù)和整數(shù)運(yùn)算的核心本質(zhì)是天然相通的，都是十進(jìn)位值制，因此，從度量的角度理解小數(shù)加減法運(yùn)算順理成章。

從圖4不難看出，無(wú)論是元角分單位、方格紙直觀模型，還是豎式的不同運(yùn)算表征方式，其運(yùn)算的本質(zhì)都是相同計(jì)數(shù)單位（度量單位）的累加或遞減（數(shù)出度量單位的個(gè)數(shù)）的運(yùn)作過(guò)程，只不過(guò)從整數(shù)到小數(shù)，度量單位、數(shù)量級(jí)向微觀擴(kuò)充。這也說(shuō)明，從度量的角度去認(rèn)識(shí)和理解加減法，小數(shù)加減法與整數(shù)加減法是一脈相承的。

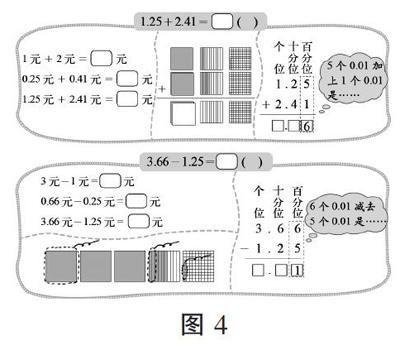
（3）分?jǐn)?shù)加減法運(yùn)算。分?jǐn)?shù)加減法的意義同整數(shù)、小數(shù)加減法的意義是一樣的，分?jǐn)?shù)加減法、特別是同分母分?jǐn)?shù)加減法的運(yùn)算也是相同度量單位（分?jǐn)?shù)單位）的累加或減少，即相同度量單位的運(yùn)作，這里不再贅述，但異分母分?jǐn)?shù)加減法需要特殊說(shuō)明。

異分母分?jǐn)?shù)加減法是小學(xué)數(shù)學(xué)中加減法運(yùn)算的高級(jí)階段，它與整數(shù)、小數(shù)加減法運(yùn)算有異也有同。“同”體現(xiàn)在：只有度量單位（計(jì)數(shù)單位或分?jǐn)?shù)單位）相同后，度量單位的個(gè)數(shù)才能運(yùn)作（累加或減少）;“異”體現(xiàn)在：整數(shù)、小數(shù)因十進(jìn)位值制都有明確的度量單位，而對(duì)于兩個(gè)異分母分?jǐn)?shù)來(lái)說(shuō)，它們的度量單位取決于它們各自的分母，它們?cè)谶M(jìn)行加減法運(yùn)算時(shí)首先需要一個(gè)對(duì)二者來(lái)說(shuō)都能獲取度量值的一個(gè)新的度量單位，即新的分?jǐn)?shù)單位的產(chǎn)生。因此，通分的目的也就非常明確了，實(shí)際上就是在尋找一個(gè)新的分?jǐn)?shù)單位，這個(gè)新的單位就像一把通用的“尺子”，以此為“標(biāo)準(zhǔn)”來(lái)度量?jī)蓚€(gè)異分母分?jǐn)?shù)，把度量的結(jié)果進(jìn)行運(yùn)作（累加或減少），就是兩個(gè)異分母分?jǐn)?shù)的和或差。

2. 從度量的角度認(rèn)識(shí)乘除法。

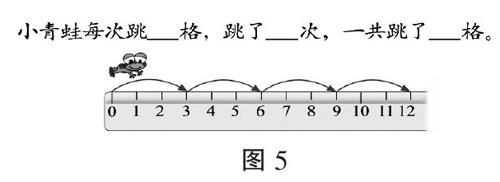
（1）整數(shù)乘除法。如圖5，這是乘法中“幾個(gè)幾”意義的運(yùn)算內(nèi)容。結(jié)合數(shù)尺模型與算式表征，解決“小青蛙一共跳了多少格”就是求“4個(gè)3是多少”。其中的4表示跳了幾次，3表示每次跳幾個(gè)，可以看作是以“3”為單位，度量了4次的結(jié)果。

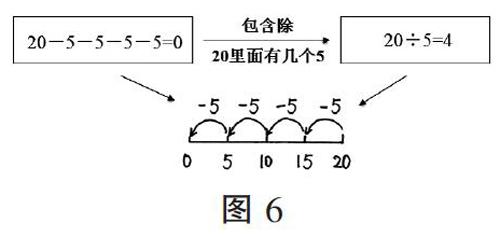
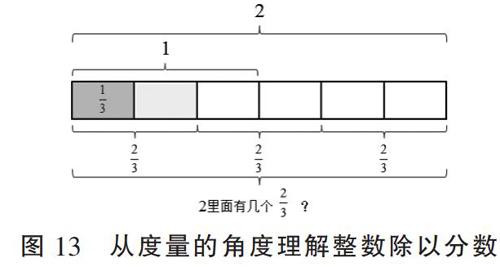
如圖6，這是除法中“包含除”意義的運(yùn)算內(nèi)容。解決“20元可以買幾輛玩具車”就是求“20里面有幾個(gè)5”。其運(yùn)算的過(guò)程，即在數(shù)線上以20作為起點(diǎn)，按照一定的“步伐”回到原點(diǎn)的過(guò)程。這個(gè)過(guò)程可看作以“5”為單位去度量數(shù)20，正好度量數(shù)了4次。說(shuō)到底，其本質(zhì)還是對(duì)度量單位的運(yùn)作，即對(duì)計(jì)數(shù)單位的處理。

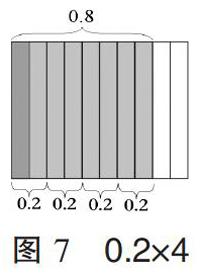
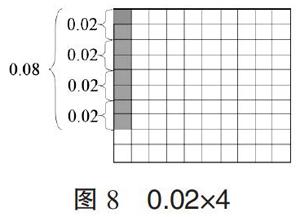
（2）小數(shù)乘除法。小數(shù)乘法運(yùn)算包括小數(shù)乘整數(shù)和小數(shù)乘小數(shù)。例如，運(yùn)算“0.2×4”，以“0.2”為單位（圖7中2個(gè)小條）去度量并數(shù)出4次，0.2連續(xù)累加4次，算式表征為0.2×4=0.2+0.2+0.2+0.2，即獲得運(yùn)算的結(jié)果0.8。同樣借助方格紙運(yùn)算0.02×4，可以“0.02”為單位（圖8中2個(gè)小塊）去度量并數(shù)出4次，0.02連續(xù)累加4次，算式表征為0.02×4=0.02+0.02+0.02+0.02，即獲得運(yùn)算的結(jié)果0.08。

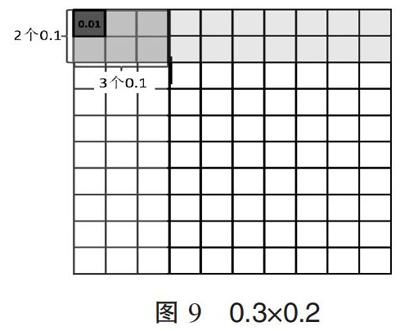
由此可見(jiàn)，小數(shù)乘整數(shù)的運(yùn)算其本質(zhì)還是小數(shù)計(jì)數(shù)單位的累加，即度量單位的運(yùn)作。而小數(shù)乘小數(shù)的運(yùn)算遇到了與前述異分母分?jǐn)?shù)加減法類似的問(wèn)題，即尋找新的度量標(biāo)準(zhǔn)，產(chǎn)生新的計(jì)數(shù)單位。如運(yùn)算“0.3×0.2”，顯然用0.1作單位去度量已行不通，這就需要尋找一個(gè)新的度量單位，而這個(gè)單位是相對(duì)隱性化的，可借助于操作方格紙直觀模型來(lái)實(shí)現(xiàn)。如圖9所示，在方格紙上分一分，畫(huà)一畫(huà)，先表示出0.3，即把“1”平均分成10份，取其中3份，0.2×0.3就是0.3的2/10，即把0.3再平均分成10份，取其中的2份。這時(shí)，新的計(jì)數(shù)單位0.01就產(chǎn)生了，用這個(gè)新的計(jì)數(shù)單位0.01作為標(biāo)準(zhǔn)去度量運(yùn)算的結(jié)果，需要數(shù)6次，算式表征為0.01×6=0.06。由此可見(jiàn)，從度量的角度看，小數(shù)乘小數(shù)的運(yùn)算核心，即新的更小的度量單位的產(chǎn)生、數(shù)度量單位的個(gè)數(shù)。說(shuō)到底，度量單位的轉(zhuǎn)換與運(yùn)作依然是小數(shù)乘小數(shù)運(yùn)算的本質(zhì)。

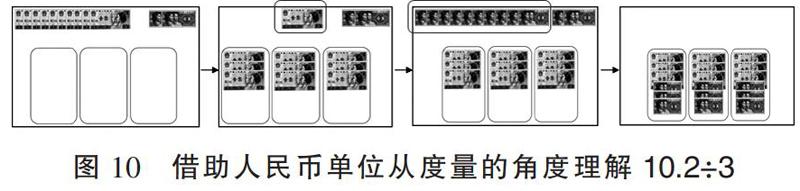
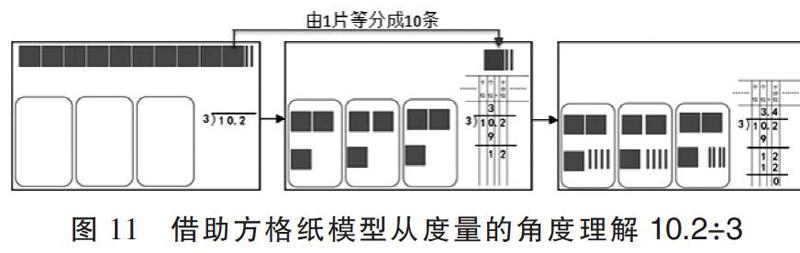
如何從度量的角度理解小數(shù)除法的運(yùn)算呢？如“買3袋牛奶花了10.2元，每袋牛奶多少元？”如圖10，借助人民幣實(shí)物模型先表示出10.2，然后動(dòng)手分，邊分邊用式子記錄分的過(guò)程。在分的過(guò)程中會(huì)遇到問(wèn)題：先分完9個(gè)1元，剩下1個(gè)1元和2角沒(méi)法直接平均分成3份怎么辦？所以把“元”轉(zhuǎn)化成“角”之后再分（1元=10角，10角+2角=12角，12÷3=4角），最后獲得運(yùn)算結(jié)果（3元+4角=3.4元）。同樣，如圖11，借助方格紙模型表示出10.2，先分完9個(gè)1（9÷3=3），剩下1個(gè)1和2個(gè)0.1沒(méi)法直接平均分成3份，所以把“1”轉(zhuǎn)化成“0.1”之后再分（1=10個(gè)0.1，10個(gè)0.1+2個(gè)0.1=12個(gè)0.1，“12個(gè)0.1”÷3=4個(gè)0.1），最后獲得運(yùn)算結(jié)果（3+4個(gè)0.1=3.4）。

通過(guò)以上兩個(gè)過(guò)程，從實(shí)物模型走向直觀模型，從“計(jì)量”走向“計(jì)數(shù)”，體會(huì)小數(shù)除法與整數(shù)除法在算理方面的內(nèi)在本質(zhì)聯(lián)系，即都是轉(zhuǎn)化平均分計(jì)數(shù)單位的過(guò)程，當(dāng)高一級(jí)的單位不夠分時(shí)，需轉(zhuǎn)化為低一級(jí)的計(jì)數(shù)單位繼續(xù)分，最終獲得運(yùn)算結(jié)果。不難看出，小數(shù)除法的本質(zhì)從度量的角度看，是計(jì)數(shù)單位的“逐級(jí)細(xì)分”過(guò)程，即新的更小的度量單位的產(chǎn)生，數(shù)度量單位的個(gè)數(shù)，即平均分的份數(shù)——除數(shù)。

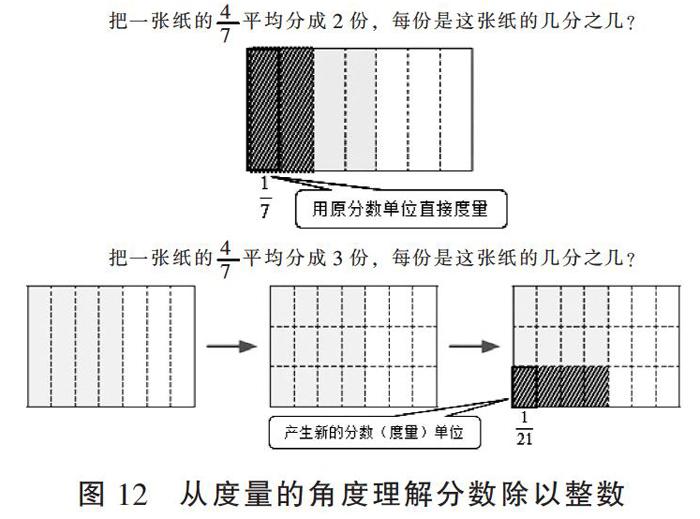
（3）分?jǐn)?shù)乘除法。分?jǐn)?shù)乘法包括分?jǐn)?shù)乘整數(shù)和分?jǐn)?shù)乘分?jǐn)?shù)，分?jǐn)?shù)乘整數(shù)的運(yùn)算與小數(shù)乘小數(shù)的運(yùn)算意義相同，本質(zhì)相通，只不過(guò)這里的度量單位由計(jì)數(shù)單位變成了分?jǐn)?shù)單位。同樣，分?jǐn)?shù)乘分?jǐn)?shù)的運(yùn)算核心也是尋找新的度量單位（新的分?jǐn)?shù)單位）的產(chǎn)生，這里均不再贅述。

三、從度量的角度整體把握數(shù)的運(yùn)算教學(xué)的意義

1. 從度量到運(yùn)算，對(duì)數(shù)學(xué)核心思想承襲的深度重視。從度量到運(yùn)算，“單位”與“單位的個(gè)數(shù)即度量值”是貫穿兩大內(nèi)容共通的核心要素和教學(xué)主線。可以說(shuō)，雖然領(lǐng)域不同，但運(yùn)算教學(xué)是對(duì)度量教學(xué)中“度量思想”的深度承襲。從度量的角度認(rèn)識(shí)數(shù)與運(yùn)算，不僅是對(duì)數(shù)與運(yùn)算意義本質(zhì)的深度認(rèn)知與理解，更是對(duì)度量思想的深度再認(rèn)識(shí)。從度量的角度認(rèn)識(shí)數(shù)與運(yùn)算，就要緊緊抓住“單位”這個(gè)核心知識(shí)，形成“牽一發(fā)而動(dòng)全身”的效果，才能從整體上把握數(shù)學(xué)學(xué)科中最本質(zhì)的知識(shí)和問(wèn)題，把握小學(xué)數(shù)學(xué)課程核心內(nèi)容的教學(xué)。

2. 從抽象到直觀，對(duì)幾何直觀模型選用的不可或缺。在數(shù)與運(yùn)算教學(xué)中，建立計(jì)數(shù)單位的概念，感悟數(shù)及數(shù)的運(yùn)算就是單位個(gè)數(shù)的運(yùn)作變換過(guò)程（累加或遞減）是教學(xué)的關(guān)鍵。而“計(jì)數(shù)單位”的數(shù)學(xué)概念是抽象的，“單位個(gè)數(shù)的運(yùn)作”的數(shù)學(xué)過(guò)程更是抽象的，我們需要幫助學(xué)生找到適合的理解方式，變抽象為直觀。因此，從度量的角度整體把握數(shù)與運(yùn)算的教學(xué)，自始至終離不開(kāi)幾何直觀模型的支撐。小棒、計(jì)數(shù)器、小方塊、數(shù)線（數(shù)尺、數(shù)軸）、方格紙、點(diǎn)子圖等都是小學(xué)階段重要的幾何直觀模型，它們能將抽象的數(shù)與運(yùn)算變得簡(jiǎn)明、直觀、可操作，但在實(shí)際教學(xué)中需適時(shí)、適當(dāng)選用。

3. 從計(jì)量走向計(jì)數(shù)，對(duì)數(shù)與運(yùn)算意義的本質(zhì)回歸。從度量的角度認(rèn)識(shí)數(shù)與運(yùn)算是深度學(xué)習(xí)的一種價(jià)值體現(xiàn)，其本質(zhì)既是對(duì)計(jì)數(shù)單位、數(shù)位、十進(jìn)位值制、整數(shù)、小數(shù)、分?jǐn)?shù)等核心概念的認(rèn)識(shí)，又是對(duì)加、減、乘、除四則運(yùn)算意義的豐富認(rèn)識(shí)與理解，而計(jì)數(shù)單位（分?jǐn)?shù)中有分?jǐn)?shù)單位）、十進(jìn)位值制等核心概念恰恰是理解數(shù)與運(yùn)算意義及算理最核心的內(nèi)容，而從度量的角度去認(rèn)識(shí)數(shù)與運(yùn)算正是對(duì)數(shù)與運(yùn)算意義的本質(zhì)回歸。在實(shí)際教學(xué)中，因數(shù)與運(yùn)算的概念的高度抽象性，所以除了幾何直觀模型的必要支撐外，還應(yīng)幫助學(xué)生在解決簡(jiǎn)單的實(shí)際問(wèn)題中從計(jì)量走向計(jì)數(shù)，讓他們更深層次地從度量的角度認(rèn)識(shí)和理解數(shù)與運(yùn)算的學(xué)習(xí)。