形狀記憶合金薄板系統全局激變現象分析*

岳曉樂 向以琳 張瑩

(西北工業大學應用數學系,西安 710072)

1 引 言

形狀記憶合金(shape memory alloy,SMA)表現出的獨特力學性能來源于馬氏體相變及其逆變化,相變的驅動力可以由溫度變化和機械載荷提供,溫度誘發的相變引起形狀記憶效應,外加應力誘導的相變產生超彈性.利用這兩個性質,SMA被制成各種參數可控的智能元件,在機翼結構的變形、精密機械系統的高速驅動及機器人仿生等方面得到廣泛應用[1?5].目前關于SMA元件的力學性能研究主要集中在溫度和載荷變化下SMA梁、振子及支架系統的平衡點穩定性、分岔行為及混沌現象等非線性動力學特征方面[6?10],對于SMA薄板系統的全局動力學研究較少,相較于局部分析,全局分析能夠揭示更多的動力學信息[11],有利于從力學理論角度突破SMA薄板系統在機械驅動和振動控制等領域的局限性.

激變[12,13]作為混沌系統中較為常見的全局分岔現象,主要刻畫了混沌吸引子和混沌鞍的不連續變化.常見的激變包括邊界激變、內部激變和合并激變.邊界激變是指混沌吸引子與吸引域邊界上的不穩定周期軌道碰撞,導致吸引子的突然消失.內部激變是混沌吸引子與其所在吸引域內的不穩定周期軌道發生碰撞引起的.合并激變是指兩個及以上的吸引子同時與吸引域邊界上的不穩定周期軌道發生碰撞,合并形成新的吸引子.盡管通過分岔圖可以觀測到激變現象,但具體類型并不清楚,需進一步繪制全局圖進行判斷.近年來,不少系統的激變現象均有所研究,例如分數階和單邊碰撞系統[14?17].

當系統中存在多個吸引子時,吸引域邊界可以是光滑的,也可以呈現出“你中有我,我中有你”的分形結構.如果吸引子的個數為三個及以上,且邊界上任一點的任意小領域,覆蓋三個及以上吸引域,則稱此域邊界具有Wada特性.隨著系統參數變化,域邊界結構會突然發生改變,稱為域邊界突變,包括光滑-Wada域邊界突變、分形-Wada域邊界突變和Wada-Wada域邊界突變等.域邊界突變作為混沌動力學的一個研究重點,對于確定系統的整體結構具有重要的物理意義,在非光滑系統和準周期強迫系統[18,19]中都有所研究,但分形性使得動力系統的力學行為很難預測,隨著胞映射技術的發展,域邊界突變和激變現象的研究得到了突破.其中經典的廣義胞映射、圖胞映射、插值胞映射等方法均可獲得系統的全局信息[20?22],但在刻畫域邊界時有一定的局限性.復合胞坐標系方法通過對連續相空間的多級分割構造一個復合胞空間,基于點映射的原理,不僅可以獲取動力系統的吸引子、吸引域和鞍等信息,還能細化任意小區域,在全局圖中優化對域邊界的刻畫.

本文以SMA薄板動力系統為研究對象,溫度和外部激勵的振幅為分岔參數,在全局分岔圖的基礎上,通過復合胞坐標系方法進一步分析系統在演變過程中出現的激變類型和域邊界突變現象,并通過對指定區域的細化,展示域邊界的分形特征.研究結果在工程領域中對控制系統的動態響應有重要意義.

2 SMA薄板動力系統

在SMA薄板中,相對于奧氏體,馬氏體更具延展性,當外加應力低于馬氏體的屈服強度時,SMA薄板可表現出超彈性.馬氏體的轉變與溫度相關,低溫相稱為馬氏體,高溫相稱為奧氏體,降溫時SMA薄板發生馬氏體相變,呈現形狀記憶效應.定義TM為馬氏體相變臨界溫度,該溫度之下,馬氏體穩定;TA為奧氏體相變臨界溫度,該溫度之上,奧氏體穩定,a,b,c均為材料常數,滿足:

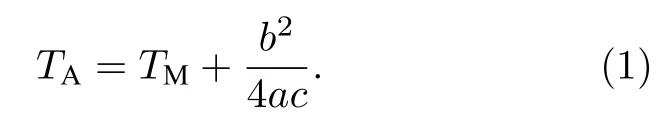
根據Falk[23]的研究,SMA薄板的本構模型可以由一個五次多項式表示,該模型給出了應變(e)-應力(s)的關系:

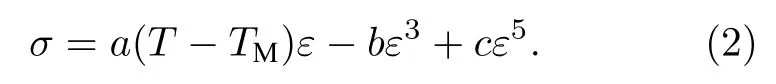
Savi等[10,24]給出了很多關于SMA彈簧振子的數學模型,文獻[25]在此基礎上演變出SMA薄板橫向振動的非線性動力學模型.本文考慮密度r,厚度h,長寬分別為l1,l2的SMA薄板,在環境黏性阻尼e下,受到橫向簡諧激振力F0=FsinWt作用,如圖1所示.

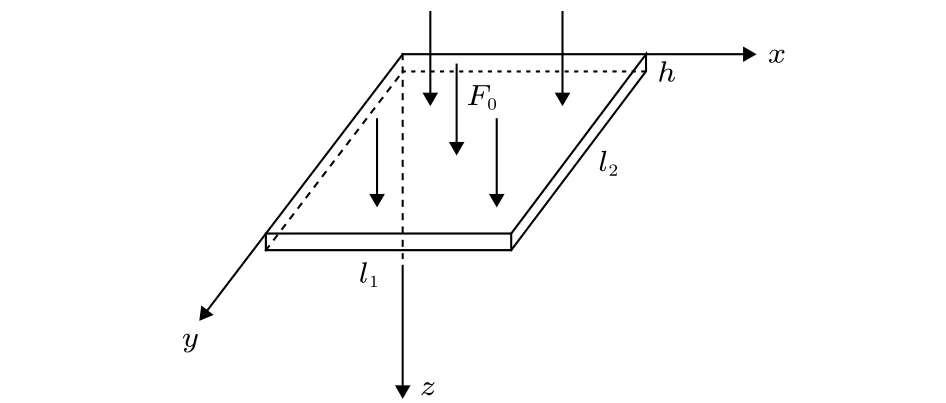
圖1 SMA薄板的橫向振動Fig.1.Transverse vibration of SMA thin plate.

薄板的橫向位移為w(x,y,t),單位長度上的內力矩分別為Ux(x,y,t),Uy(x,y,t),Uxy(x,y,t),其橫向振動方程為[25]

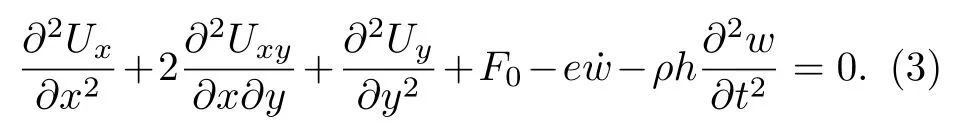
薄板面內的3個應力分別為sx,sy,txy,內力矩為[25]

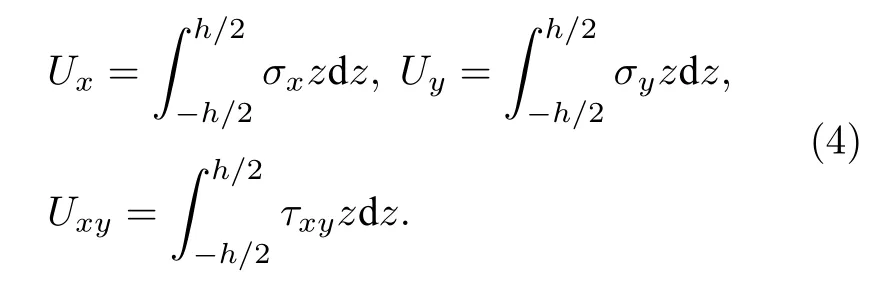
在滿足四周簡支邊界條件下取位移模式[25]:

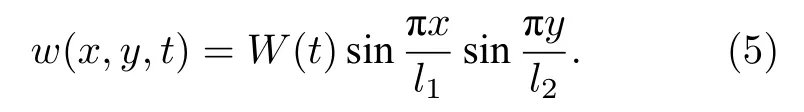
通過Galerkin原理和應變-應力本構關系,并對系統參數量綱歸一化,得到SMA薄板的橫向振動非線性動力學方程[25]:

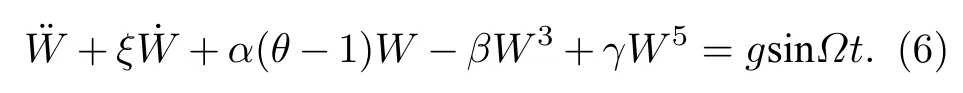
方程(6)可化為以下形式的一階微分方程組:

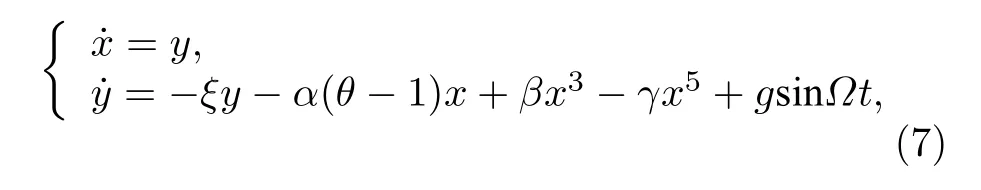
其中a,x,b,g均為正常數;q,g分別是無量綱化的溫度和簡諧激振力振幅.參數選取同文獻[24]所示,x=0.2,a=1,b=1300,g=470000,W=1.接下來基于復合胞坐標系方法,分析溫度q和激勵振幅g兩個參數變化時,SMA薄板系統的全局動力學特性變化過程.

3 振幅對全局特性的影響

當溫度q=0.7,此時SMA薄板位于馬氏體臨界溫度下,含有兩個穩定的馬氏體相.選取不同的初值點(–0.0553,–0.09),(–0.031,0.045),(0.083,–0.032),(0.047,0.059)構造Poincare映射,保留穩態映射點,得到對應的多值分岔圖,如圖2所示.隨著幅值g值的變化,系統呈現明顯的多吸引子共存特征,并伴隨有豐富的激變和域邊界突變等現象.

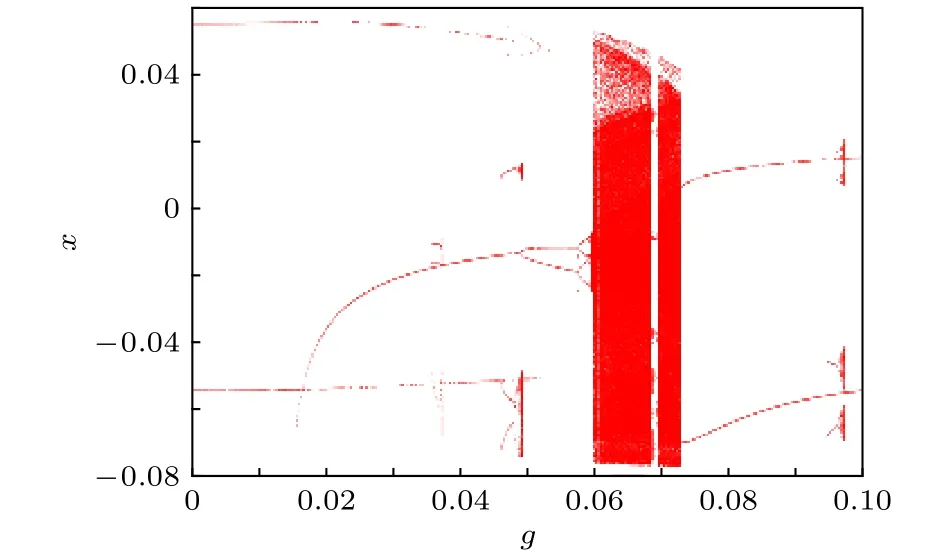
圖2 系統(7)隨振幅g變化的多值分岔圖Fig.2.Multivalued bifurcation diagram of the system (7)with the variation of amplitude g.

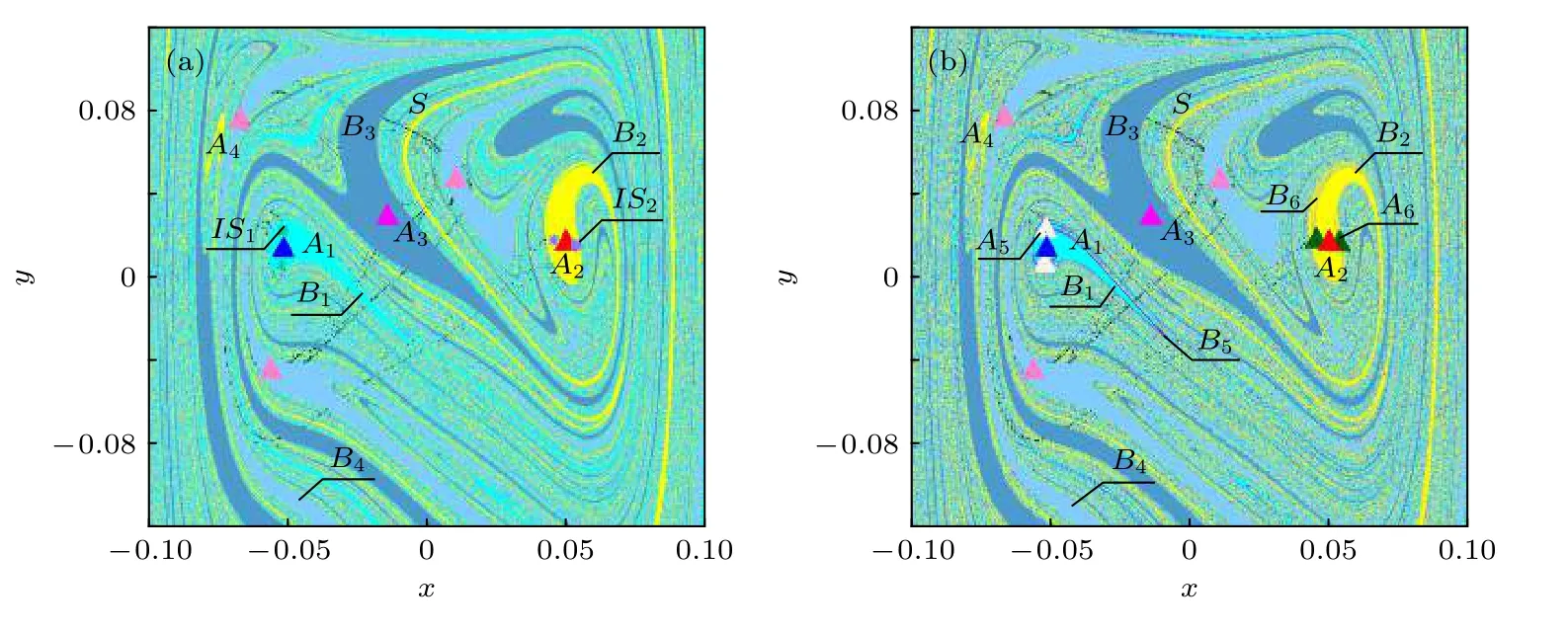
圖3 系統(7)的全局圖 (a) g=0.0471; (b) g=0.0472Fig.3.Global diagram of the system (7): (a) g=0.0471; (b) g=0.0472.

在區域D={(x,y)|–0.1 ≤x≤ 0.1,–0.12 ≤y≤0.12}上,均勻劃分1000×1200個胞,利用復合胞坐標系方法獲取系統的吸引子、吸引域和邊界鞍等全局信息,闡述g在0.0460到0.0727的范圍內激變現象出現的機理.為更直觀理解全局圖,對以下圖形做以下說明: 用△表示吸引子A,不同顏色代表不同的吸引子; 吸引域用B表示,不同吸引域顏色不同;S表示邊界鞍;IS表示吸引域內部鞍; 下標表示吸引子、吸引域和內部鞍的個數,例如A1,A2表示系統兩個吸引子共存,B1,B2為其對應的吸引域.

3.1 邊界激變

當g從0.0471增大到0.0472時,發生兩次逆的邊界激變,如圖3所示.A5和A6表示周期為2的吸引子,A5與嵌在吸引域B1,B5邊界的鞍S碰撞,A6和嵌入吸引域B2,B6邊界的鞍S碰撞,使得A5,A6和部分邊界鞍S突然消失,成為內部周期鞍IS1,IS2,同時吸引域B5,B6消失,吸引域B1,B2變大.

當g從0.0482變化到0.0483時,系統再次發生兩次邊界激變,兩個周期1吸引子A1和A2與邊界上的鞍S發生碰撞,變為吸引域B5,B6的內部鞍IS5,IS6,同時吸引域B1和B2消失,如圖4所示.

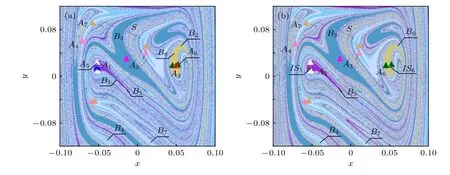
圖4 系統(7)的全局圖 (a) g=0.0482; (b) g=0.0483Fig.4.Global diagram of the system (7): (a) g=0.0482; (b) g=0.0483.

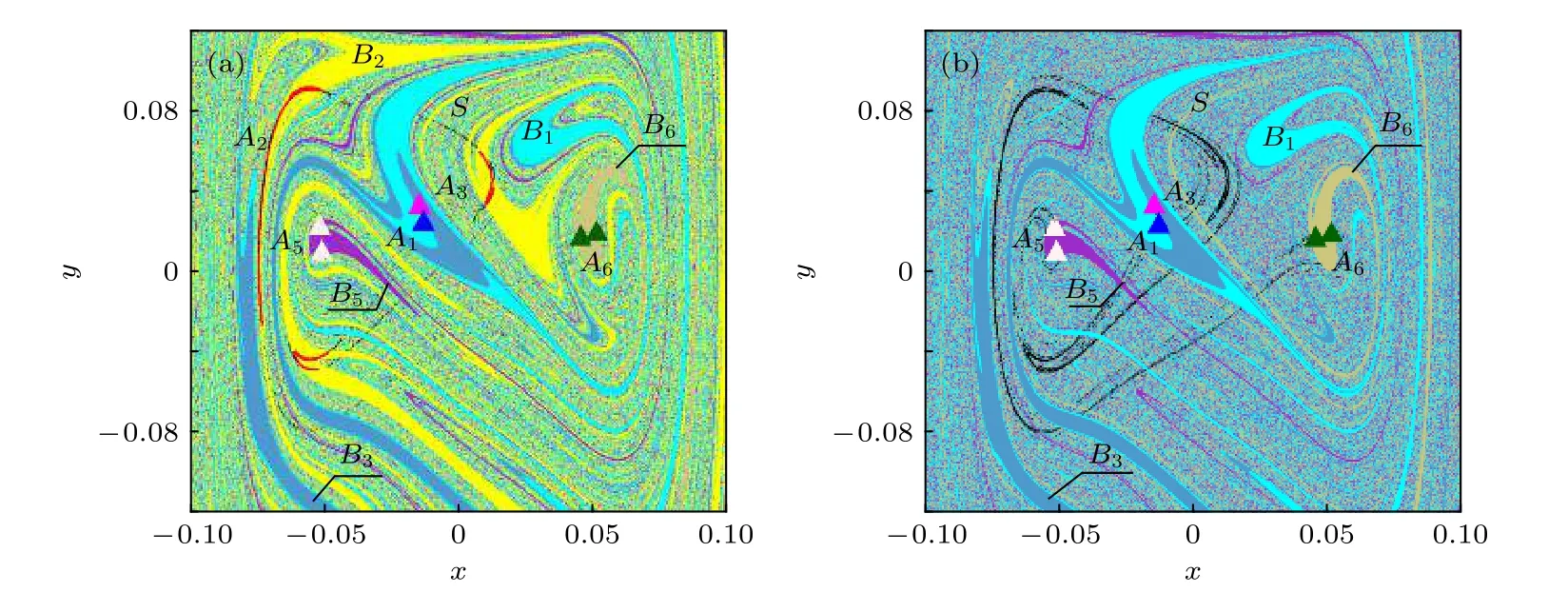
圖5 系統(7)的全局圖 (a) g=0.0491; (b) g=0.0492Fig.5.Global diagram of the system (7): (a) g=0.0491; (b) g=0.0492.

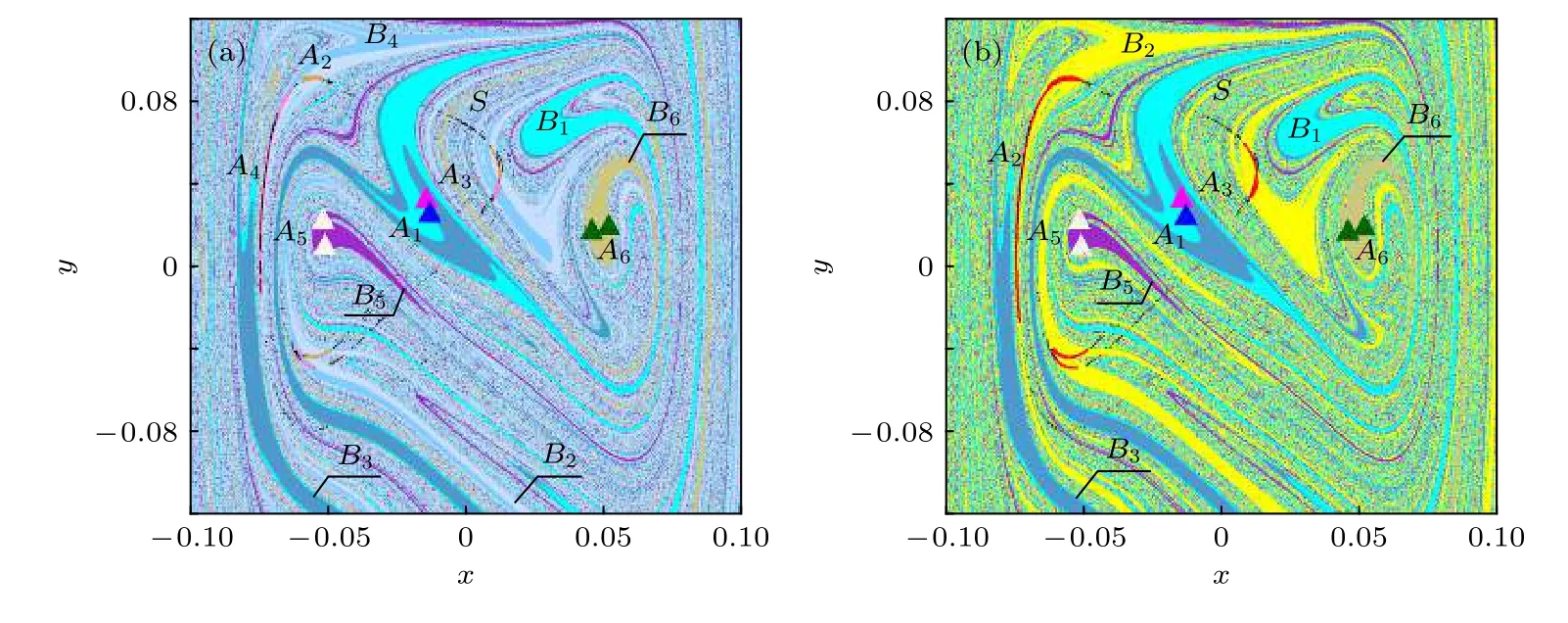
圖6 系統(7)的全局圖 (a) g=0.0490; (b) g=0.0491Fig.6.Global diagram of the system (7): (a) g=0.0490; (b) g=0.0491.

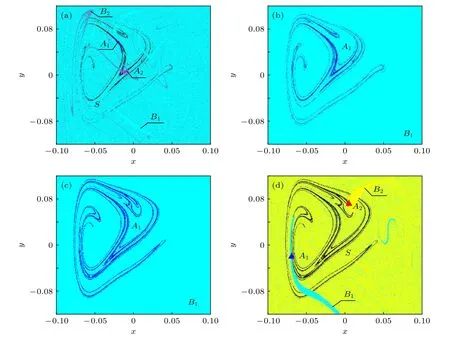
圖7 系統(7)的全局圖 (a) g=0.0596; (b) g=0.0597; (c) g=0.0726; (d) g=0.0727Fig.7.Global diagram of the system (7): (a) g=0.0596; (b) g=0.0597; (c) g=0.0726; (d) g=0.0727.

當g從0.0491增大到0.0492時,混沌吸引子A2與吸引域邊界上的混沌鞍S發生碰撞,發生邊界激變,變成新的更大的邊界混沌鞍,吸引域B2隨之消失,狀態空間中為四個周期吸引子和混沌邊界鞍共存,如圖5所示.

3.2 合并激變

當g從0.0490變化到0.0491時,混沌吸引子A2和A4不斷接近吸引域邊界上的混沌鞍S,發生合并激變,成為新的混沌吸引子A2,與此同時吸引域B2,B4合并為新的吸引域B2,如圖6所示.

當g從0.0596變化到0.0597時,混沌吸引子A1,A2與邊界上的混沌鞍S碰撞,發生合并激變,變為新的混沌吸引子A1,如圖7(a)和圖7(b)所示.當g從0.0726增大到0.0727時,發生逆合并激變,混沌吸引子A1消失,出現兩個新的周期1吸引子A1,A2及混沌邊界鞍S,如圖7(c)和圖7(d)所示.

圖8 系統(7)的全局圖 (a) g=0.0460; (b) g=0.0461Fig.8.Global diagram of the system (7): (a) g=0.0460; (b) g=0.0461.

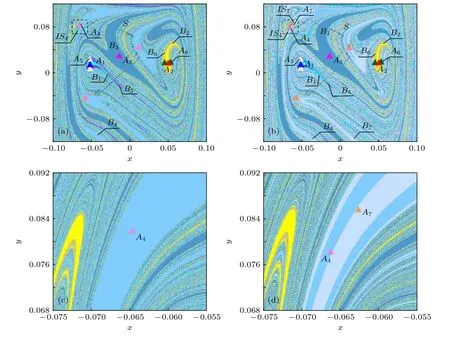
圖9 系統(7)的全局圖 (a) g=0.0478; (b) g=0.0479; (c),(d) 分別對應于(a),(b)圖的區域細化Fig.9.Global diagram of the system (7): (a) g=0.0478; (b) g=0.0479; (c),(d) the region refinement of panels (a) and (b).

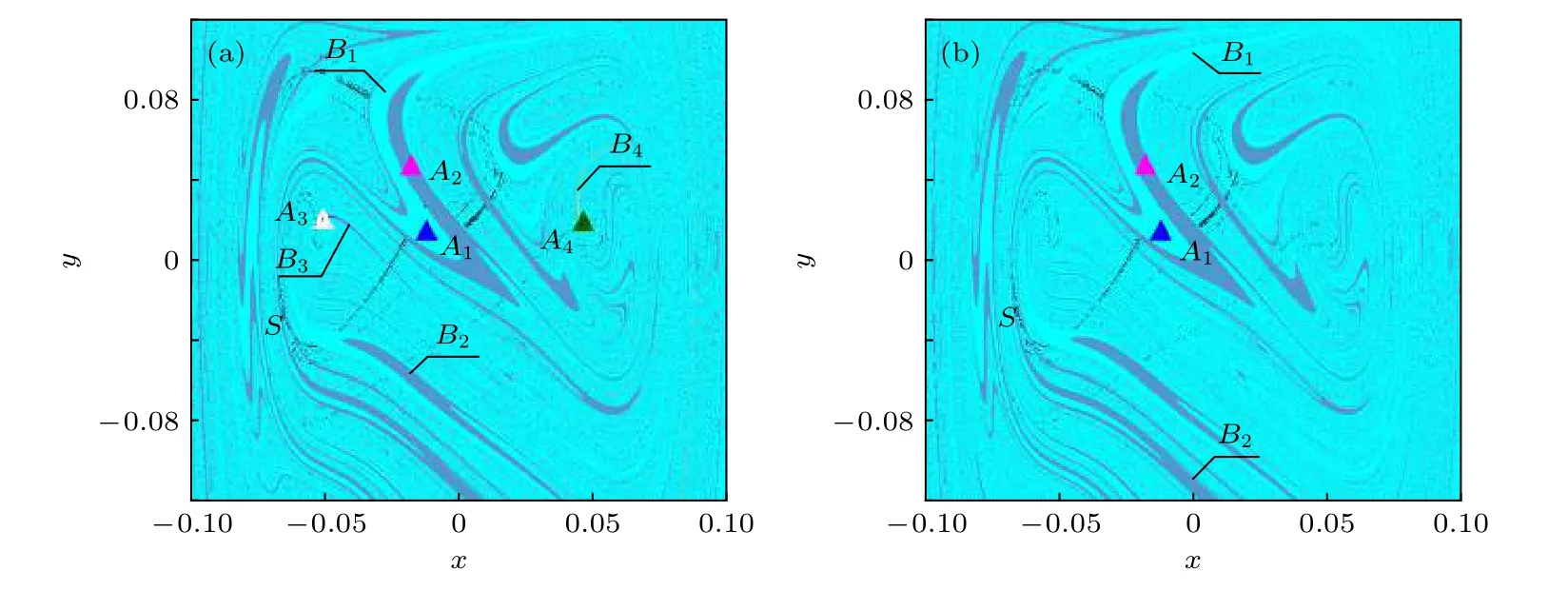
圖10 系統(7)的全局圖 (a) g=0.0533; (b) g=0.0534Fig.10.Global diagram of the system (7): (a) g=0.0533; (b) g=0.0534.

3.3 域邊界突變

當g=0.0460時,系統存在三個周期1吸引子A1,A2,A3和嵌在吸引域B1,B2,B3邊界上的混沌鞍S,此時的域邊界呈現出Wada特性.當g增大到0.0461時,系統新出現一個周期3吸引子A4,此時的域邊界由4個吸引域構成,仍具有Wada特性,系統發生Wada-Wada域邊界突變,如圖8所示.

當g從0.0478增大到0.0479時,吸引子的個數從6個變為7個,為判斷吸引子變化過程,對區域v={(x,y)|–0.075 ≤x≤ –0.055,0.068 ≤y≤0.092}進行細化.可以發現,原周期3吸引子A4消失,并在其附近出現兩個新的周期3吸引子A4和A7,如圖9(c)和圖9(d).原吸引域B4分裂為新吸引域B4和B7,且參數變化前后域邊界均呈現Wada特性,域邊界結構更加復雜,系統再次發生Wada-Wada域邊界突變.

當g=0.0533時,狀態空間中有4個周期1吸引子共存,此時域邊界仍具有Wada特性.當g增大到0.0534時,周期吸引子A3和A4消失,狀態空間中僅剩2個周期1吸引子A1,A2,此時域邊界的Wada特性消失,只呈現分形特性,系統發生Wada-分形域邊界突變,如圖10所示.

4 溫度對全局特性的影響

溫度作為SMA薄板的一個可控參數,利用溫度改變SMA薄板的力學特性在工程領域中有重要運用.取g為0.06,分析溫度q變化對系統的影響,選取不同的初值點(–0.0553,–0.09),(–0.031,0.045),(0.083,–0.032),(0.047,0.059)構造Poincare映射,得到對應的分岔圖,如圖11所示.可以發現,隨溫度q的變化,系統中吸引子個數、類型及大小會發生改變,并出現激變現象.為從全局角度分析溫度變化對系統激變的影響,本節基于復合胞坐標系方法,將區域D={(x,y)| –0.1 ≤x≤ 0.1,–0.12 ≤y≤ 0.12},均勻劃分為1000×1200個胞,獲得系統的吸引子、吸引域、鞍和域邊界等全局特性.

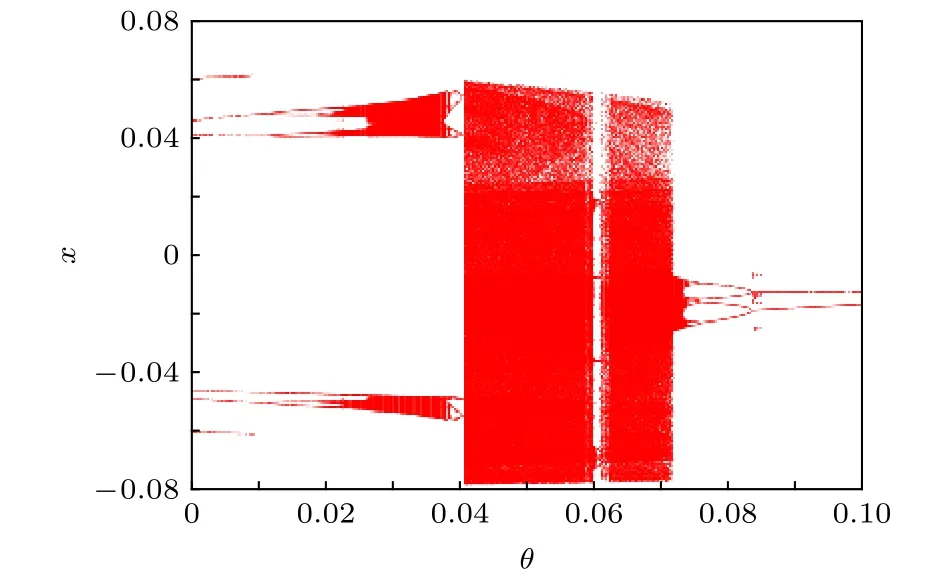
圖11 系統(7)隨溫度q變化的多值分岔圖Fig.11.Multivalued bifurcation diagram of the system (7)with the variation of temperature q.

4.1 邊界激變

當q=0.8379時,狀態空間中兩個周期1吸引子A1和A2共存,S為嵌入在分形域邊界上的混沌鞍,IS1,IS2是吸引域B1,B2內部的混沌鞍.當q增大為0.8380時,系統出現兩個新的吸引子A3和A4,內部鞍IS1,IS2消失,系統發生兩次逆邊界激變,如圖12所示.

4.2 合并激變

當q從0.4088變化到0.4089時,周期2吸引子A1和A2同時與域邊界上的混沌鞍S發生碰撞,合并為一個新的混沌吸引子A1,吸引域B1和B2合并成為新吸引域B1,系統發生合并激變,如圖13(a)和圖13(b)所示.當q從0.7182增大到0.7183時,混沌吸引子A1消失,出現兩個新的混沌吸引子A1和A2,以及嵌在域邊界上的混沌鞍S,系統發生逆的合并激變,如圖13(c)和圖13(d)所示.

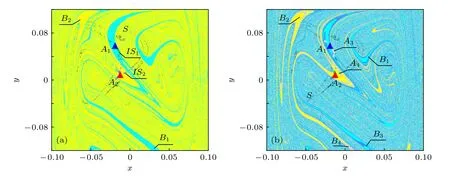
圖12 系統(7)的全局圖 (a) q=0.8379; (b) q=0.8380Fig.12.Global diagram of the system (7): (a) q=0.8379; (b) q=0.08380.

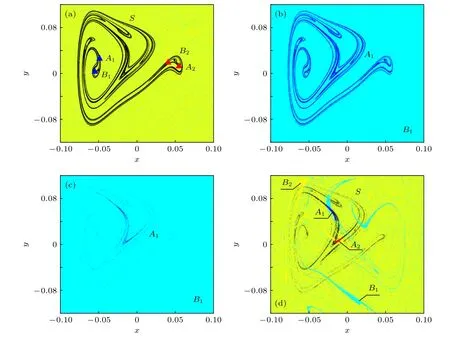
圖13 系統(7)的全局圖 (a) q=0.4088; (b) q=0.4089; (c) q=0.7182; (d) q=0.7183Fig.13.Global diagram of the system (7): (a) q=0.4088; (b) q=0.4089; (c) q=0.7182; (d) q=0.7183.

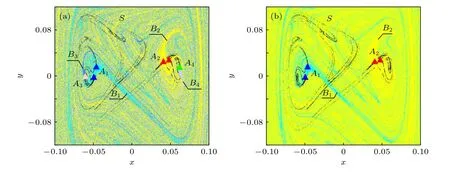
圖14 系統(7)的全局圖 (a) q=0.0950; (b) q=0.0951Fig.14.Global diagram of the system (7): (a) q=0.0950; (b) q=0.0951.

4.3 域邊界突變

當g=0.0950時,狀態空間中兩個周期2吸引子A1,A2,和兩個周期1吸引子A3,A4共存,吸引域邊界呈現Wada特性.當g增大為0.0951時,兩個周期1吸引子A3和A4消失,吸引域邊界變為由B1和B2構成的分形邊界,系統發生Wada-分形域邊界突變,如圖14所示.

5 結 論

考慮實際工程中溫度和應力對于SMA的力學特性的影響,本文選取SMA薄板為研究對象,以溫度q和激振力振幅g作為分岔參數,采用復合胞坐標系方法分析其全局分岔特性,探究在參數的連續變化下,系統激變現象及域邊界突變的演化過程.

在一定的參數變化范圍內,系統呈現豐富的激變現象,如周期或混沌吸引子與域邊界上的周期鞍或混沌鞍發生碰撞的邊界激變,周期吸引子或混沌吸引子同時與邊界上的混沌鞍發生碰撞的合并激變等.當多吸引子共存時,域邊界會呈現分形結構,并隨著參數的變化,發生Wada-Wada,Wada-分形和分形-Wada等域邊界突變現象.本文的研究結果對于通過控制溫度和激勵強度等參數,調控SMA薄板系統的動態響應,優化機械設備的變形及振動控制等問題上提供有效的分析手段.