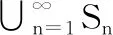連續統假設下 Sierpiński 集的構造及其性質研究

□孟戀忱

一、研究分析

通過以下分析可以看到，Vitali集包含不平凡的可測子集。

定理1:Vitali集有不可數零測子集。

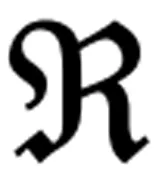
由于下述定理，為找到只有平凡可測子集的不可數集，只能構造一種不同于Vitali集的不可測集。

定理2:任何不可數可測集都有不可數零測子集。

為給出一種構造方法，需要下面的引理。

定理3(Sierpiński集)：設實軸上的集合A具有正的Lebesgue外測度，則存在A的不可數子集S，S與任一零測集的交集均為至多可數集。

證：記B為全體Borel零測集的集族，由引理知B的勢為c=1，由良序定理，存在B到首個不可數序數(即全體可數序數)ω1的序同構，以可數序數標記B中的元素，表示為B={Rβ|β<ω1}。下面歸納的定義點集S={Xα|α<ω1}。設序數α<ω1，且Sα={Xβ|β<α}已知，由于α是可數序數，故∪β<αRβ是零測集，其與至多可數點集Sα之并也為零測集，于是可在非零測集A((∪β<αRβ)∪Sα)中選取一點Xα。根據上述構造，顯然有S?A，并且通過Xα?Sα可以看出Xα兩兩相異，從而S與ω1有相同的勢。對任一零測集E，存在零測Gδ集G?E，由于G∈B，存在可數序數γ使G=Rγ。但對每個α>γ都有Xα?∪β<αRβ，從而Xα?Rγ，最后得到S∩E?S∩Rγ?Sγ+1為至多可數集。

由以上方法構造的集合S沒有不可數零測子集，結合定理2可知S是不可測集，并且沒有不可數可測子集，只有平凡的可測子集，滿足這個性質的集合稱作Sierpiński集(可以等價的定義為可測子集均可數的不可數集，或是不可數子集均具有正外測度的正外測度集，證明是顯然的，在此略去)。在上述證明中，如果連續統假設不成立，則無法保證∪β<αRβ是零測集，也就無法構造出S。

可以自然的得到以下性質。

定理4：Sierpiński集的不可數子集也是Sierpiński集。

證：顯然。

定理5：Sierpiński集的可數并也是Sierpiński集。

二、結語