基于“四能”的學習內容開發與實踐①
——以“三角形分割為兩個等腰三角形”的探究為例
張 勃 伍春蘭
(北京市房山區良鄉第二中學 102488; 北京教育學院數學系 100120)
《義務教育數學課程標準(2011年版)》提出了“運用數學的思維方式進行思考,增強發現和提出問題的能力、分析和解決問題的能力”的“四能”總目標. 《普通高中數學課程標準(2017年版)》也提出了“提高從數學角度發現和提出問題的能力、分析和解決問題的能力”的“四能”課程目標. 因此,在核心素養大背景下,如何基于學生“四能”的提升,開發學習內容并實施是值得深入研究的.
下面以“三角形分割為兩個等腰三角形”的探究為例,闡述我們的實踐與思考.
1 三角形分割
任意一個三角形都可以從一個頂點引出一條射線與對邊相交,頂點與交點之間的線段(分割線)把三角形分割成兩個小三角形. 但是如果分割后的小三角形是特殊的,則被分割的三角形就要有一定的條件限制. 探討何種三角形分割后符合目標定位的小三角形,或者已知的三角形分割后是否存在符合目標定位的小三角形,可以考量學生的思維品質,以及分析問題、解決問題的能力. 因此近年(模擬)中考,涉及三角形分割的試題數見不鮮.
比如,2014年南京市建鄴區中考數學一模27題,將三角形分割為一個等腰三角形和一個直角三角形,稱分割線為伴侶分割線,并探討伴侶分割線存在的三角形角度的關系. 再如,2016年寧波市中考數學25題,將三角形分割為一個等腰三角形和一個與原三角形相似的三角形,稱分割線為完美分割線,并證明或求解與完美分割線相關的問題. 又如,2016寧波市北侖區中考一模25題,將三角形分割為兩個等腰三角形,稱分割線為特異線,并證明或求解與特異線相關的問題.
特異線存在的經典三角形有兩類,一類是黃金三角形(頂角為36°或108°的等腰三角形),因其腰與底之比成黃金比而得名. 有趣的是分割后得到的兩個小三角形不僅還是黃金三角形(其中一個與原黃金三角形相似,見圖1和圖2),而且分割線將對邊分割成黃金比的線段. 另一類是直角三角形,由“斜邊中線等于斜邊一半”的定理,易證明結論的正確.
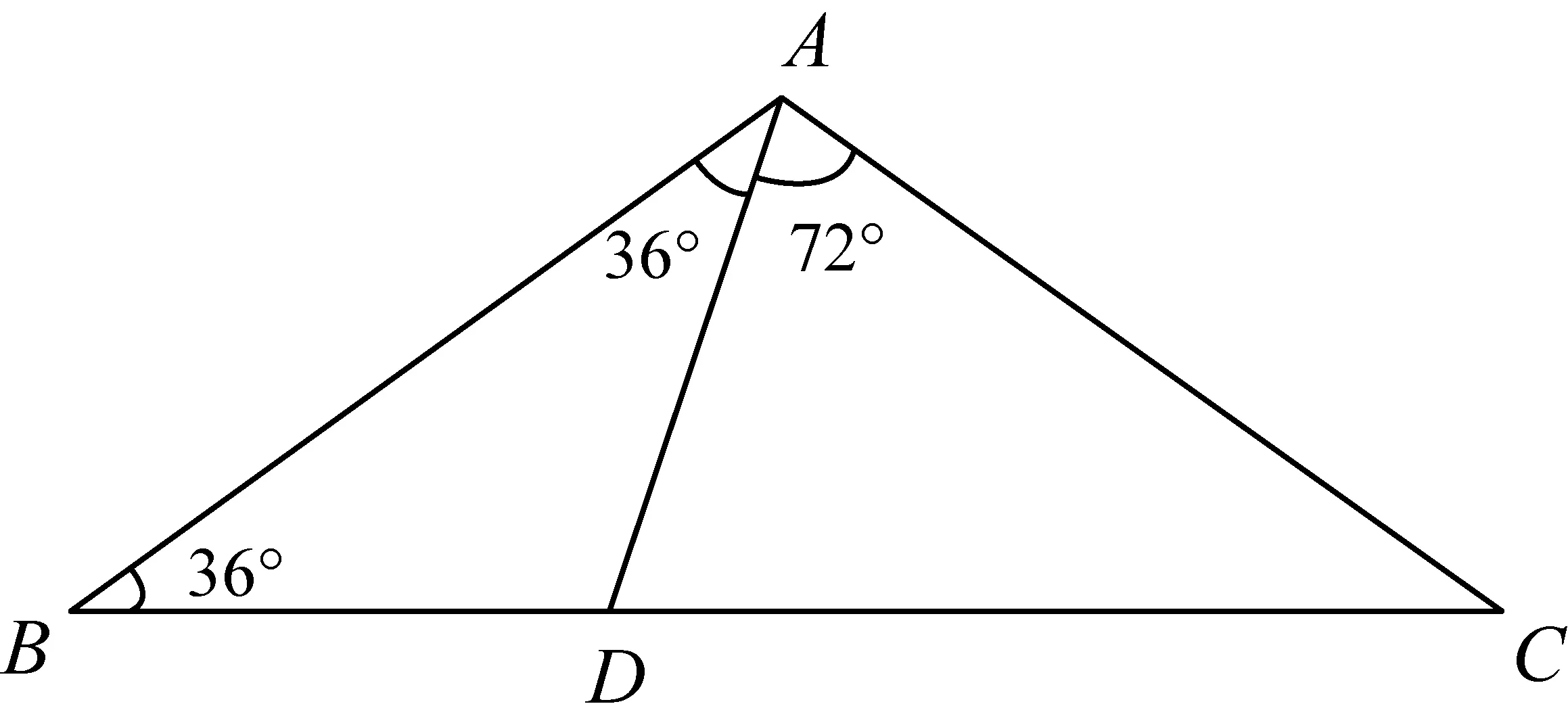
圖2
文獻[1]證明了非直角三角形可分割為2個等腰三角形的充要條件是: 有兩個內角之比為1∶2或1∶3,而且這兩角中的較小者小于π/4.
2 文獻分析
對于分割成兩個等腰三角形的三角形,文獻[2-4]都采用了分類的方式詳細探討. 文獻[2]按三角形三個角的關系:3個角相等、2個角相等(頂角小于底角;頂角大于底角)、3個角都不相等的三角形分類探索;文獻[3]先按角將三角形分類,再按三角形最小角為分割后的小等腰三角形的頂角、底角分類探究;文獻[4]按三角形類型(直角三角形、一般三角形、等腰三角形)分類探討. 上述文獻雖然結論還不完備,但邏輯還是清楚的.
一些教師以“三角形分割為兩個等腰三角形”為主題嘗試課堂教學,從問題解決[5]、數學活動課[6]、積累數學活動經驗[7]、支架式教學理論指導[8]等視角積極探索,為相關內容的教學提供了經驗.
3 教學實踐
3.1 第一次教學實踐
3.1.1引出猜想
教師通過創設情境或提出問題(見表1),使學生明確了研究方向,猜想出具有2倍角、3倍角關系的一般三角形可以分割為兩個等腰三角形.

表1 教師創設的情境或提出的問題
3.1.2初步驗證
師:請自己設計一個三角形,使這個三角形可以被分割成兩個等腰三角形.先獨立思考,然后小組合作.
教師讓完成的小組把分割成兩個等腰三角形的三角形內角度數寫在黑板上,并引導學生發現角之間的關系并歸類(見表2).

表2 學生小組列舉可分割等腰三角形的三角形
3.1.3探索條件
師:剛才有小組發現,具備2倍角關系的三角形也有的不能分割成兩個等腰三角形,比如三個內角分別是50°、100°、30°的三角形.問題是哪些三角形可以被分割成兩個等腰三角形?
師:在△ABC中,設∠A=α,∠B=β,∠C=γ(α>β)(圖4),當α,β,γ滿足什么數量關系時,△ABC可以被分割成兩個等腰三角形?
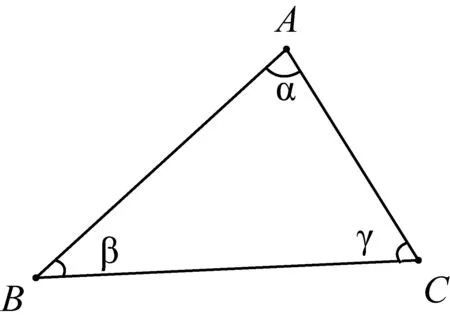
圖4
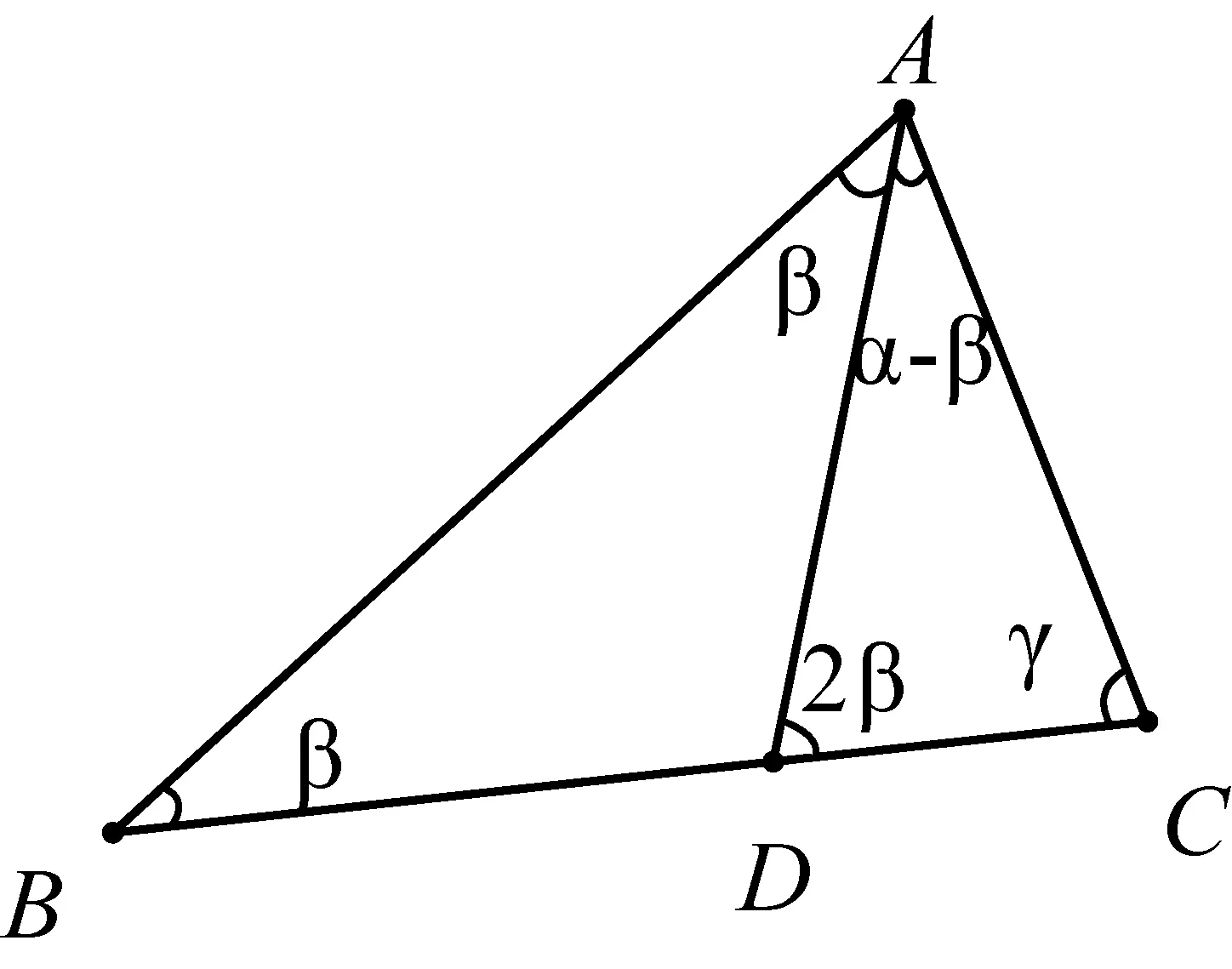
圖5
師:因為α>β,作∠BAD=β(圖5),這樣就構造了一個等腰三角形△ABD. 欲使△ADC也是等腰三角形,要滿足什么條件?
生:只需△ADC有兩個角相等,分類討論.
(1)若∠ADC=∠C,則γ=2β;
(2)若∠ADC=∠DAC,則α-β=2β,有α=3β;
(3)若∠DAC=∠C,則α-β=γ,有α=β+γ.
師:情形(1)、(2)得到的結論,說明能分割成兩個等腰三角形的三角形,具有2倍或3倍角關系. 前面遇到過有2倍角關系的三角形,但不能分割成兩個等腰三角形,因此還要深入探究角的其它限制條件.
當γ=2β,因為α>β,所以180°-β-2β>β,解得β<45°;當α=3β,因為γ>0°,所以180°-β-3β>0°,解得β<45°.于是得到以下結論:當1倍角小于45°時,有2倍角、3倍角關系的三角形可分割成兩個等腰三角形.
師:α=β+γ,這是什么特征的三角形?
生:直角三角形.
師:直角三角形如何分割成兩個等腰三角形?
生:利用斜邊中線分割.
3.2 第二次教學實踐
3.2.1問題的提出
學生經歷黃金三角形(頂角為36°)的分割為兩個等腰三角形后,教師引導學生嘗試提出相關問題,結果他們基本上提出了預設的問題(見表3),不過也沒有超出預設的范圍.
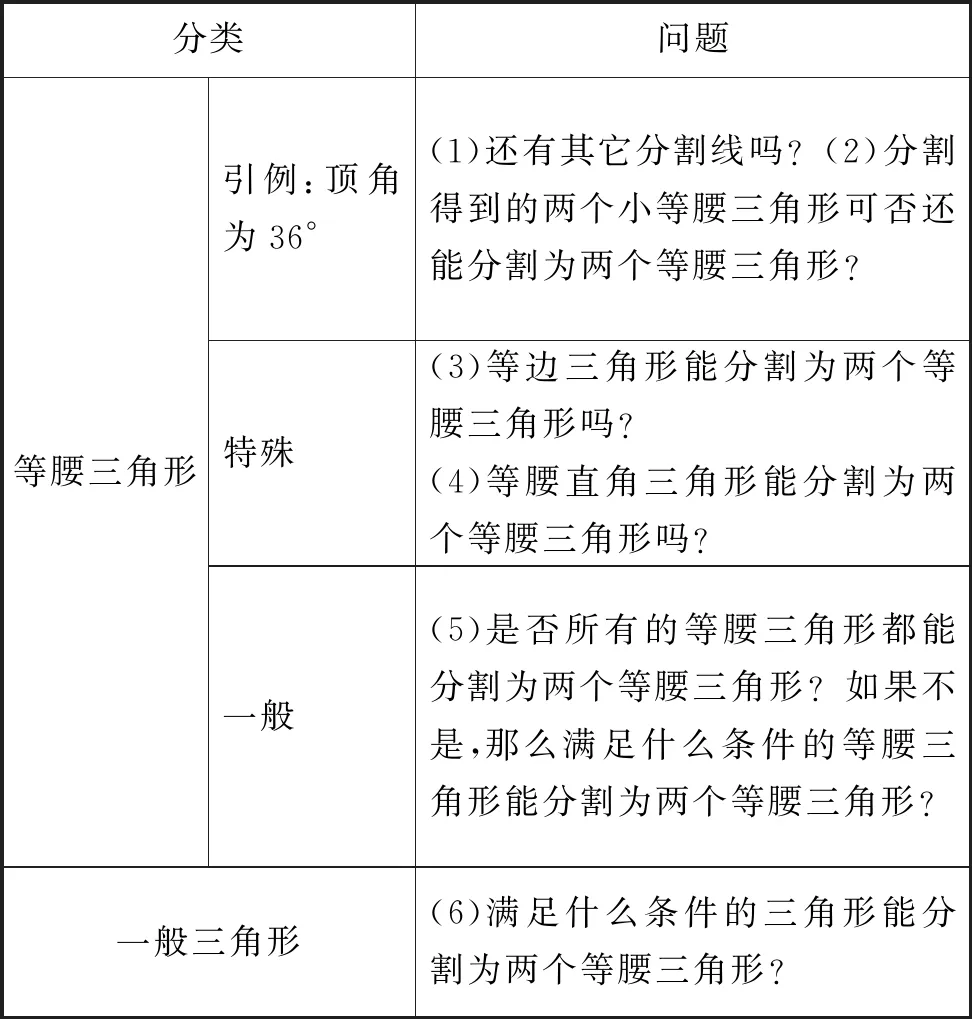
表3 學生嘗試提出相關問題歸類(預設)
3.2.2等腰三角形的分割探究
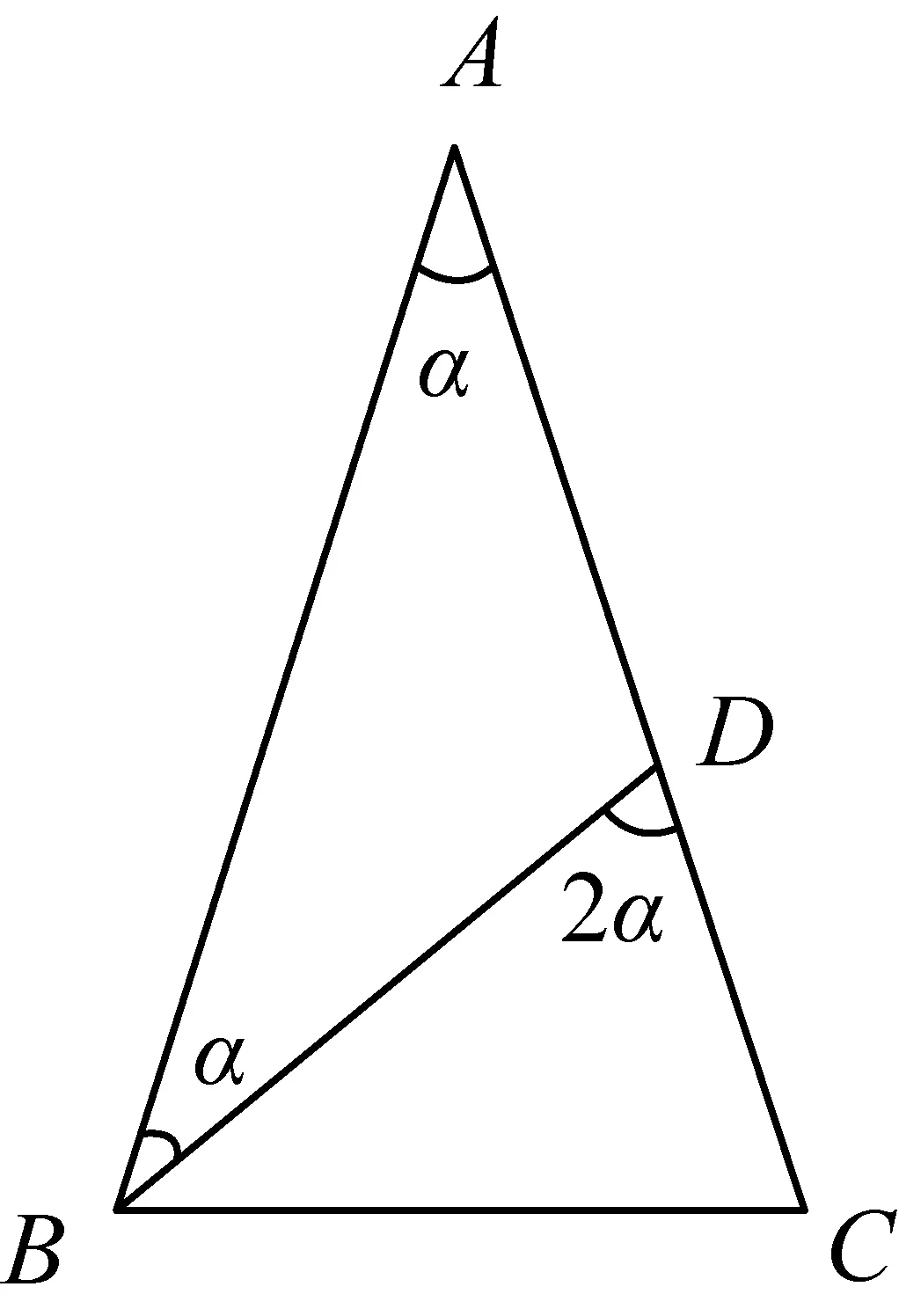
圖6
嘗試對問題(3)(等邊三角形)的分割未果,學生發現不是所有的等腰三角形都能分割為兩個等腰三角形.
對引例和問題(2)的分割,學生體會到:不能分割最小角;頂角是銳角和鈍角時,分割的角是不一樣的. 于是在分析滿足什么條件的等腰三角形能分割為兩個等腰三角形時,學生認為需要分類討論:頂角為銳角(見圖6)、直角(已解決)及鈍角(見圖7). 經過探究,學生發現:只有頂角是36°、180°/7、90°及108°的等腰三角形,才能分割為兩個等腰三角形.
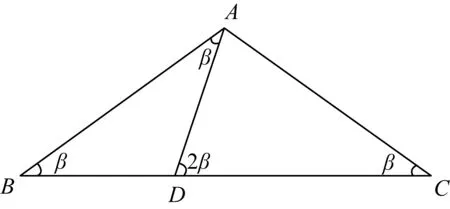
圖7
3.2.3一般三角形的分割探究
4個能分割的等腰三角形,除了有兩個角相等,學生發現還有兩個角具備2倍或3倍的關系,提出猜想:具有2倍或3倍角的關系的一般三角形,可能分割為兩個等腰三角形. 為了驗證猜想,按照特殊到一般的原則,教師引導學生挑選具備2倍或3倍角的關系的特殊三角形(見表4),然后嘗試分割積累活動經驗,最后探究一般三角形分割成兩個等腰三角形的條件.

表4 具備2倍或3倍角的關系的三角形(舉例)
4 思考建議
4. 1 “四能”的培養既需要活動經驗的支撐,更需要理性思考的融入
學生在本節課學習之前,對三角形的分割是有體驗的. 比如中線將三角形分割為2個等(面)積三角形,高線可將三角形分割為2個直角三角形. 換個角度觀察中線、高線,不僅對這兩個重要線段有了新的認識,也喚起了學習本節課的活動經驗.
專題課是一種普遍教學形態,教師往往將同一類考(習)題聚在一起組成一個專題,旨在學會解決這類問題的套路. 學生缺少題目來龍去脈的考察,題目之間關聯的分析,以及思想方法的感悟. 因此,將一個特殊問題變式為一類問題的專題課,在日常教學中并不多見. 所以三角形分割的第一次教學實踐,得到很多觀摩教師的好評. 但我們也發現一些不足,主要是學生的思維參與欠缺.
在第二次教學實踐中,學生兩次經歷了從特殊到一般的探究,特殊情形的分割,不僅讓學生發現、提出了問題,也為分析、解決問題提供了方向. 同時,第一次從特殊到一般的探究(等腰三角形的分割)為第二次探究(一般三角形的分割)提供思路和方法. 在整個活動中思考貫穿始終,并在活動前后通過交流促進學生思考. 作為延拓,鼓勵學生就三角形分割,發現、提出新的研究問題(作為作業),比如,研究三角形分割為一個等腰三角形和一個直角三角形的條件,并分析解決問題.
4.2 教師要成為學習資源的研究者和開發者
教師通過對典型問題的多角度的審視與探究,將適宜學生學習的、富含數學思維價值的資源開發成教學內容. 經歷生成式的探究教學,實現鞏固“四基”、感悟思想、獲得經驗的近期目標,也為提升“四能”、涵養核心素養的遠期目標“添磚加瓦”.
4.3 信息技術成為探究教與學的工具
非直角三角形分割為2個等腰三角形,當兩個內角之比為1∶2或1∶3時,許多研究者(教師)都忽略了“較小者小于π/4”這個條件,包括已發表的研究成果. 事實上這個條件對初中生也是不易發現的,所以師生借助動態軟件啟發思考,突破難點是非常有裨益的. 比如,兩個內角之比為1:2(∠A:∠B)的三角形,分別從頂點C(見圖8)、頂點B(見圖9)引分割線,利用滑動條的變動,感受∠A范圍的限制. 當從頂點C分割時,∠A需要小于45°;當從頂點B分割時,∠A只能等于45°(見圖10)或等于36°(見圖11). 當然動態課件的嵌入,既可作為理性證明后的直觀演示,也可作為理性思考前的合理猜想,還可作為理性與直觀交互思考的媒介. 因此何時、怎樣融入信息技術,需要教師根據教學目標與學情抉擇.
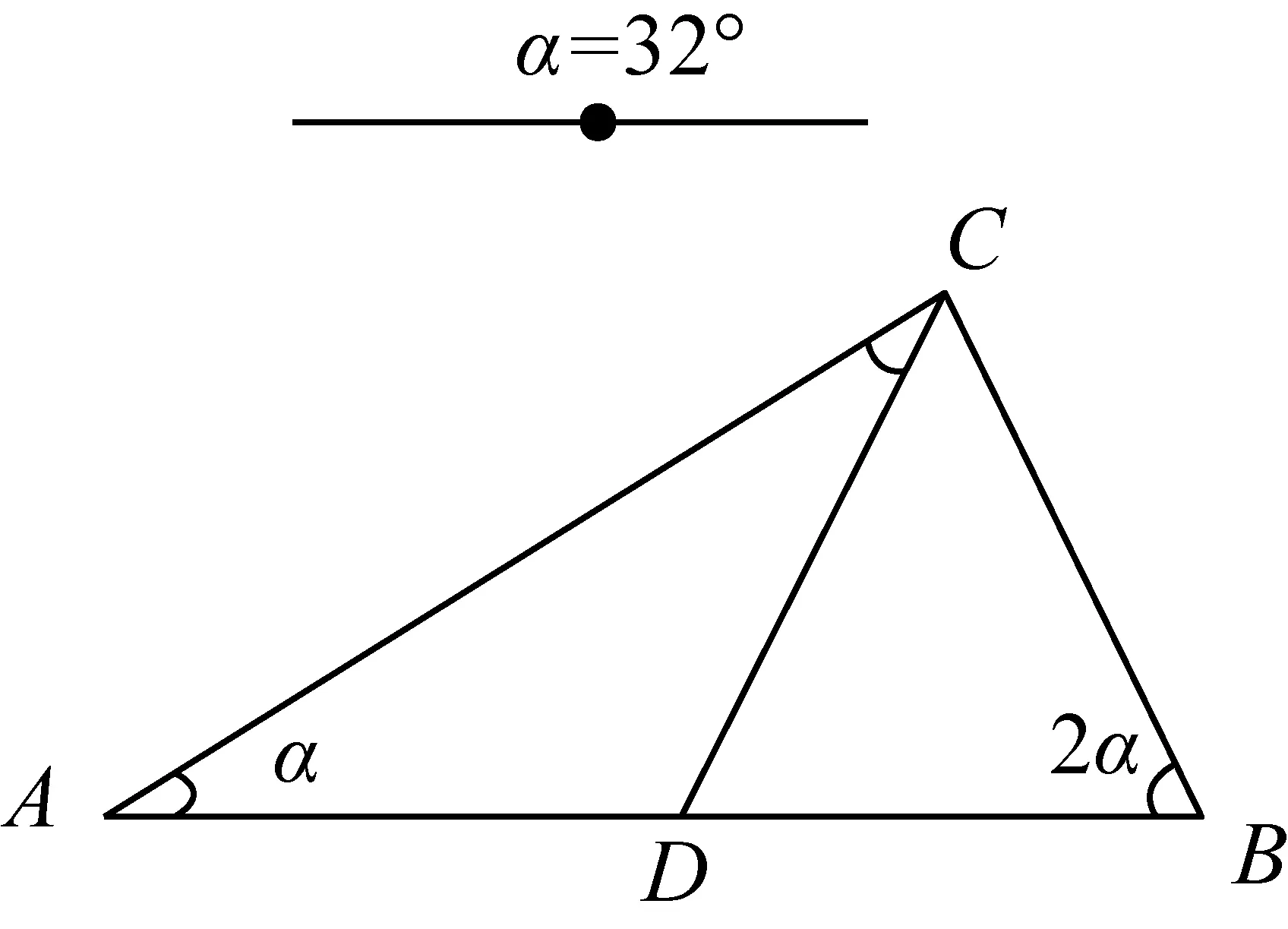
圖8
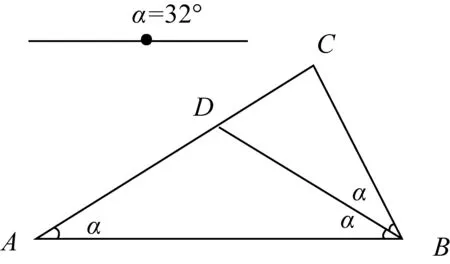
圖9
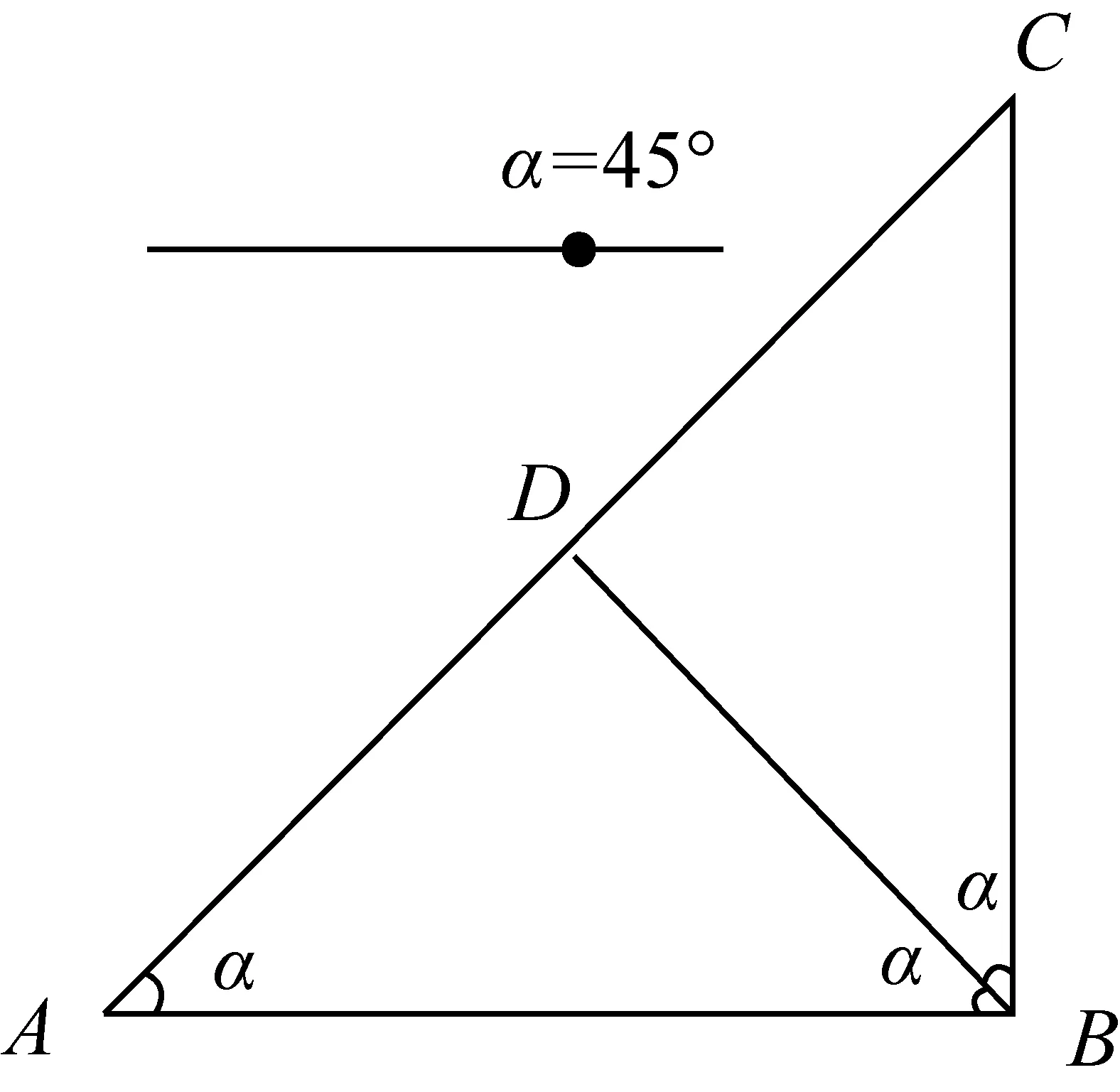
圖10
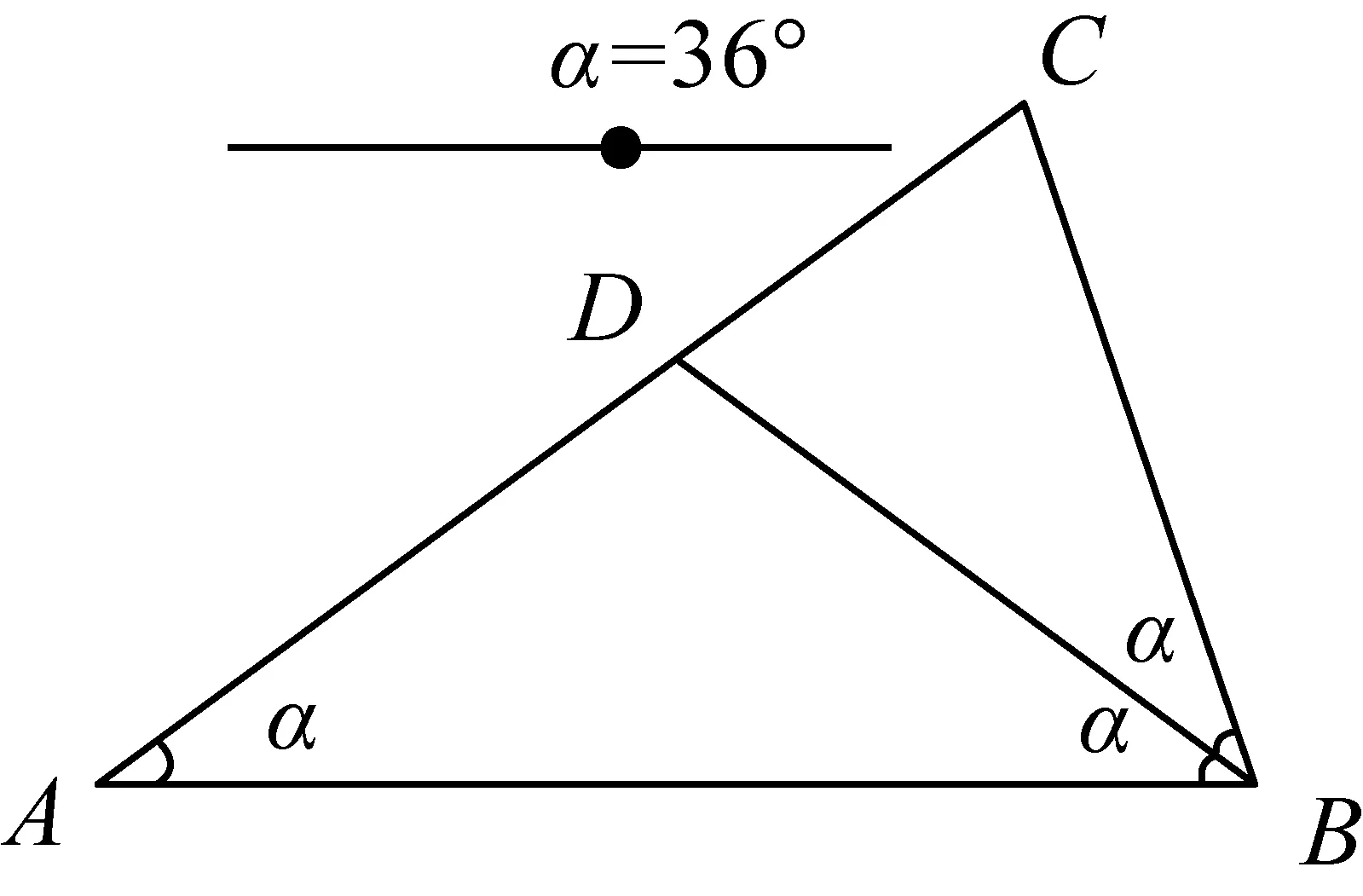
圖11
4.4 “四能”成為核心素養落地的現實力量
目前課程構建、開發與實施都聲稱基于核心素養的,然而實際上有些與“核心素養”立意存在較大的出入. 因此以課程為載體,在構建、開發與實施過程中,以“四能”為抓手是促進核心素養落地的有效途徑.

