借助學科整合深入理解概率
——《可能性》教學實踐與思考（二）

陳蕓蕓

【教學內容】

人教版五年級上冊第四單元。

【教學過程】

一、問題導入

A.一定 B.可能 C.不可能

師：請動動你的小腦袋思考一下，怎樣選擇？

生：選“可能”。因為中獎的幾率很低，買10000張也可能不會中獎。

生：我也認為選“可能”。因為每一張彩票都可能中獎，也可能不中獎，所以他可能這1000 張都沒中獎，也可能一兩張中獎等。

揭題：可能性到底是什么呢？今天這節課我們就一起來研究它。（板書課題）

二、問題探究

1.小組活動，組織摸球，體會“可能”。

師：（依次出示一個紅球、一個黃球、一個藍球，裝入同一個口袋）我把它抖一抖、攪一攪，拉緊了。現在讓你任意地摸一個，你會摸到什么顏色的球？

生：可能摸到紅球，可能摸到黃球，也有可能摸到藍球。

追問：請猜想，摸到哪個球的可能性大？

生：摸到紅球、黃球、藍球的可能性一樣大。

小組活動：把學生分成六個七人小組，其中每個小組摸的口袋里放一個紅球、一個黃球和一個藍球。

要求：

（1）組長拿口袋，組內成員按順序摸球，共計摸球20 次。

（2）摸好后請把球重新放回口袋，記錄員用圓片表示出摸到的球的顏色貼在黑色板子上，最后統計出結果填寫到記錄單上。

（3）每次摸之前，要把口袋抖一抖，用手攪一攪。

2.反饋交流，體驗“可能”，六位組長依次將作品貼到黑板上。

師：在摸球的過程中，大家一定有很多體會吧？

生：我很想摸到一個藍球，卻總是摸不到。

師：的確，很多同學如愿以償地摸到了想要的那個球，但有些同學并沒有摸到。如果我想摸一個紅球，能確定第幾次摸到嗎？

生：不能確定，有可能第一次就摸到了，也有可能一直摸不到。

生：我們組連續三次摸到了紅球，我們都認為下一次該摸到黃球或藍球了，結果卻還是摸到了紅球。

追問：靜靜地想一想，連續摸到三次紅球，對下一次摸到什么顏色的球有影響嗎？

（借助小組作品進行分析）

小結：在這個袋子里摸球，摸到什么顏色的球是不確定的，不確定的時候我們就說有可能。（板書）

三、問題分析

師：再來看看每個組最后摸球的結果，（板書六組數據）你又有什么發現呢？

師：是呀！剛才有同學不是猜想摸到紅球、黃球、藍球的可能性是一樣的嗎？這是怎么回事呢？

生：摸球的時候是有運氣的，而且20 次也不能說明什么。

師：是哦，多摸幾次！那我們摸120 次，每個小組，準備開始。

生：那得摸到什么時候呀！

師：那誰有好辦法？生：把六個組的數據加起來不就是120 次嘛！

師：贊同他的說法嗎？那我們就快速計算。（填入統計表中）

師：觀察這組數據，你又有什么發現？

生：摸到三種顏色的球的次數都很接近了。

師：那摸500 次呢？想不想試試？其實，在今天這個信息技術非常發達的社會，電腦就可以幫我們完成，期待嗎？

（教師打開Scratch 程序，輸入500 并運行程序，產生數據并記錄）

師：還想試驗多少次？

生：1000 次。

師：觀察這些數據，談談你的發現。

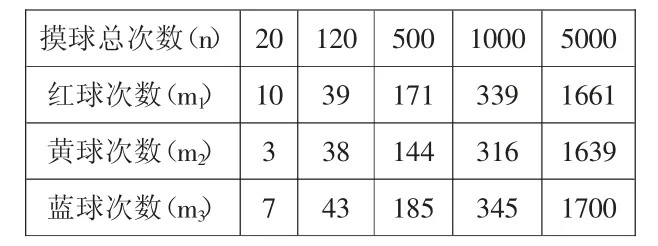
表1

生：當摸球總次數越來越多的時候，摸到三種顏色的球的次數越來越接近。

師：是呀！今天我們借助信息技術做了一件很強大的事，也驗證了我們的猜想：當袋子中只有一個紅球、一個黃球和一個藍球的時候，摸到它們的可能性是相等的，是多少呢？

師：是的，其實在歷史上類似于這樣的試驗有很多，你知道的還有什么？（拋硬幣、擲骰子）老師搜集了歷史上拋硬幣試驗的相關數據，試驗結果見下表：

表2

師：如果我們把這些數學家的拋擲次數加起來，正面向上和正面向下的次數分別是多少？

生：拋擲總次數是52088 次，正面向上總次數是26119 次，正面向下總次數是25969 次。

師：請觀察這些數據，有什么感受？

生：隨著試驗次數的增加，正面向上和正面向下的次數會越來越接近，也就是它們的可能性相等。

四、問題練習

1.男生女生大PK。（游戲公平嗎？）

（1）游戲一：兩個藍球，兩個紅球，任意摸一個球，摸出藍球男生贏，摸出紅球女生贏。

師：游戲公平嗎？

（2）游戲二：兩個藍球，兩個紅球，任意摸兩個球，摸出同色的男生贏，摸出不同色則女生贏。

師：老師改變了游戲規則，但還是這個口袋，游戲還公平嗎？（在練習紙上寫一寫，畫一畫）

生：我認為不公平，摸兩個球，有兩藍、兩紅、一藍一紅三種可能，男生贏得可能性大。

生：我反對，如果兩個藍球分別是1 號藍球、2號藍球，兩個紅球分別是1 號紅球、2 號紅球，那女生摸到的兩個球有四種可能，當然是女生贏得可能性更大。

師：兩位同學到底是誰的觀點更科學呢？請看大屏幕。（課件演示所有可能）現在我們都清楚地看到了這個口袋中任意摸兩個球所有的可能，也就明白了女生贏得可能性比男生大。

（3）任意摸兩個球，要想游戲公平，請你設計一個摸球游戲。

生：三個藍球，一個紅球，任意摸兩個球，摸出同色的男生贏，摸出不同色則女生贏。

師：這樣改編一下球的個數，游戲公平了嗎？

生：真的可以，好厲害！

2.小軍和小淇在操場上做游戲，他們蒙上眼睛在一定距離外向如圖所示的邊長分別為3m 和2m的正方形場地投擲沙包，擲中內圈部分小軍勝，擲中外圈部分小淇勝，若未擲入大圈內則重新拋擲一次，你認為游戲公平嗎？圖1 和圖2 你會選擇哪個場地？

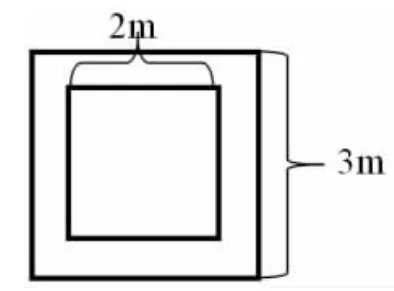
圖1

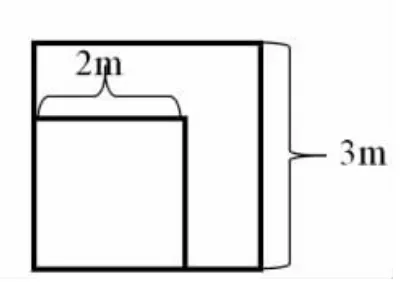
圖2

生：我認為圖1 不公平，因為投擲到內圈比較容易，外圈比較分散，很難擲中。圖2 比較公平，擲中的可能性幾乎相等。

生：我認為兩個場地都不公平，外圈的面積都是5m2，內圈的面積都是4m2，明顯外圈比內圈大，那擲中的可能性也是外圈比內圈大，對小軍不公平。

師：同學們思考的有些道理，但數學是一門嚴謹的學科，游戲究竟是否公平，我們借助計算機來完成投擲試驗，請組長拿出平板電腦運行程序，填寫記錄表。

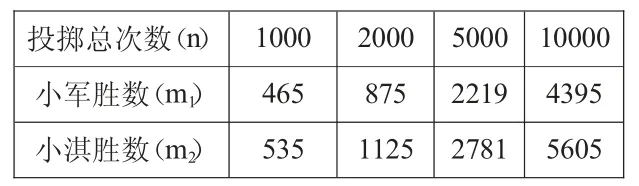
表3

師：仔細觀察表3 中的數據，你有什么發現？

生：隨著投擲次數的增加，小淇贏得可能性比小軍大。

師：要想小軍和小淇贏得可能性一樣大，你會怎么設計這個場地呢？（在練習紙上畫一畫，算一算）

反饋：

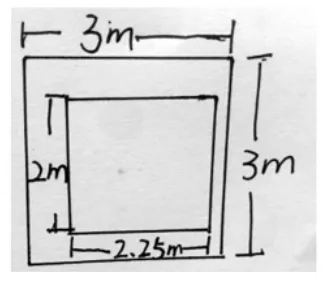
圖3

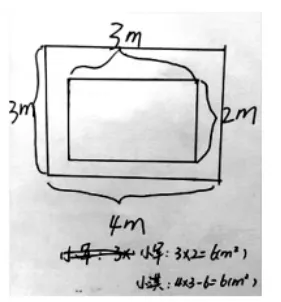
圖4

五、問題回顧

師：通過這節課的學習，你有哪些收獲？還有什么疑惑？

【課后思考】

課堂是缺憾的藝術。上述教學實踐，雖然著力想體現《數學課程標準（2011年版）》倡導的理念：數學教學過程是教師引導學生活動的過程，讓學生經歷數學化的過程，讓學生自己建構數學知識的過程。教師應激發學生的學習積極性，給學生提供數學活動的機會，幫助他們在自主探索和合作交流的過程中真正理解和掌握基本的數學知識與技能、數學思想和方法，獲得廣泛的數學活動經驗。但實際操作中一定會存在許多不足，懇請各位方家批評指正！

有兩點小體會，自覺得可以一提。

一、學科整合，實現思維可視化

隨機現象雖然對于個別試驗來說無法預知結果，但在相同條件下進行大量重復試驗時，卻又呈現出一種規律性，我們稱之為隨機現象的統計規律性。而課堂上開展試驗的次數是受到局限了，想要做到像歷史上的數學家拋硬幣一樣，有幾千次或是幾萬次，短短的四十分鐘根本無法實現。誰能代替人類完成這樣的事呢？那就是計算機！筆者利用編程軟件——Scratch 設計程序，程序代碼簡單易懂，使課堂上所有學生都聚焦于數據的變化，充分體會摸到紅球次數、黃球次數、藍球次數這三個數字的變化是隨機產生的，有的學生驚嘆：“你看，現在是藍球次數最多！”過了幾秒又有學生情不自禁地說：“Yeah！紅球趕上來了，紅球的次數最多了。”某種程度上，這樣的試驗激發了學生的思維能力，發展了學生的想象能力和創新意識。當試驗次數從500 次到1000 次再到5000 次，學生通過數據分析感知到：隨著試驗次數的增加，紅球、黃球和藍球的次數越來越接近，摸到這三種球的可能性相等，課前的猜想和120 次試驗后的猜想都得到了驗證，學生欣喜若狂。

第二次結合Scratch 輔助教學的是第二個練習，幾何概型相比于古典概型更加抽象，將抽象的隨機事件做可視化處理，直觀地呈現投點的全過程。學生通過平板電腦自主操作，運行Scratch 程序，輸入投擲總次數，觀察并分析數據，感受事件發生的隨機性和統計規律性。

二、角色轉換，化“操作工”為“研究者”

學生的生活經驗足夠支撐他們做出這樣的判斷：在一個裝有一個紅球、一個黃球和一個藍球的袋子中，任意摸出一個球，可能摸到紅球、可能摸到黃球，也有可能摸到藍球，而且它們的可能性相等。但是學生理解的可能性相等是什么呢？即第一次摸到紅球，第二次應該摸到黃球，第三次應該摸到藍球或者連續三次摸到紅球，那么第四次總該是黃球或藍球了，而實踐結果卻還是紅球。

顯然這種認識是錯誤的，因此在課堂教學過程中，讓學生體驗摸球的過程，并把摸到的球的顏色貼出來，把結果顯性化（見圖5）。通過橫向、縱向直觀地比較，充分說明了在摸之前是不能確定摸到哪個球的，結果的出現是隨機的，而前一次的摸球結果也不會影響下次的結果，從而積累對隨機現象的直觀感受。

圖5

這節課仍然有許多地方值得再思考。比如，對于可能性，學生大都有豐富的生活經驗，似乎不用教學，學生隨著年齡的增長，也都能作出相對準確的判斷，教材中安排此內容，教學價值和意義究竟該如何定位？還有，Scratch 程序的運用，很好地做到了學科整合，也讓學生充分體驗了科技的魅力，但科技是把雙刃劍，是否會有學生質疑這是后臺程序設計好的？高科技是否真實可信畢竟學生沒有真實試驗、親眼所見。如何消除學生對高科技的疑惑倒在其次，更重要的是，如何在理性思考與現實經驗之間真正建立有效的通聯。