利用等號(hào)教學(xué)滲透小學(xué)生的代數(shù)思維

朱敏君

【摘要】在算術(shù)中，“等號(hào)”是數(shù)與代數(shù)中重要的關(guān)系符號(hào)，它代表運(yùn)算，表示結(jié)構(gòu)與關(guān)系。一年級(jí)是等號(hào)概念形成的關(guān)鍵時(shí)期，教師要重視等號(hào)的本質(zhì)含義教學(xué)，為學(xué)生各個(gè)學(xué)段的銜接打好基礎(chǔ)。

【關(guān)鍵詞】一年級(jí);等號(hào)教學(xué);代數(shù)思維

“等號(hào)”是小學(xué)生學(xué)習(xí)數(shù)學(xué)算式的開(kāi)始，它以?xún)筛粯娱L(zhǎng)的橫線(xiàn)形象地表示了等號(hào)兩邊的量是相等的，揭示了等號(hào)的本質(zhì)含義。然而，在一年級(jí)這個(gè)等號(hào)概念形成的重要時(shí)期，大多數(shù)教師往往只關(guān)注等號(hào)的算術(shù)意義，忽略了其代數(shù)意義。2018年9月，筆者在正式教學(xué)前，對(duì)新接一年級(jí)2個(gè)班的學(xué)生做了等號(hào)意義的學(xué)前調(diào)查。

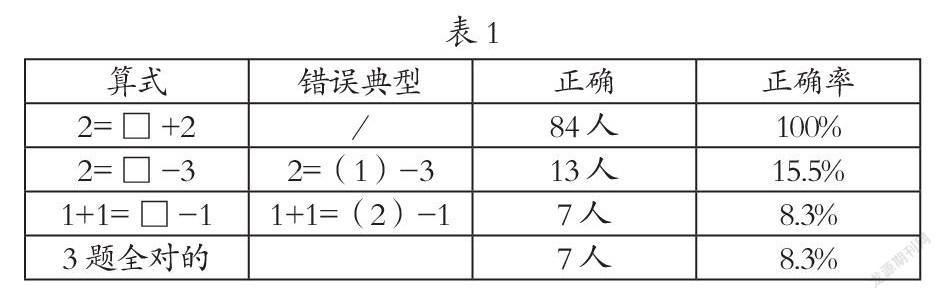
具體的題目為2=□+2， 2=□-3，1+1=□-1。測(cè)試結(jié)果如想象般糟糕。參與測(cè)試的是筆者任教的2個(gè)班級(jí)的共84人，具體答題情況如表1所示。

第1題和第2題屬于同一類(lèi)型的測(cè)試題，都是考查學(xué)生對(duì)等號(hào)可逆性的理解。不同的是，第1題是加法題，第2題是減法題。結(jié)果很顯然，對(duì)于加法題目，正確率達(dá)到了100%，可見(jiàn)學(xué)生算術(shù)思維的成熟度。而同樣是求關(guān)于結(jié)果為2的算式，第2題的正確率卻只有15.5%。學(xué)生覺(jué)得結(jié)果就應(yīng)該寫(xiě)在算式的最后面。至于第3題，除去8.3%的正確解答的7人，其他人一律寫(xiě)了“2”，清楚地反映出學(xué)生對(duì)等號(hào)代數(shù)意義的零認(rèn)識(shí)。

一、適時(shí)引入，初步感受等號(hào)“關(guān)系性”

1.教材： 已有編排，銜接略有偏失

學(xué)生首次接觸等號(hào)是在第二單元認(rèn)識(shí)了1～5的數(shù)后，在《比大小》中與大于號(hào)、小于號(hào)同時(shí)學(xué)習(xí)的，這是以“等號(hào)的關(guān)系性質(zhì)”而引入的。等號(hào)的第二次出現(xiàn)，是在學(xué)習(xí)《加法的認(rèn)識(shí)》一課中。而此時(shí)，教師和學(xué)生都只重視加法的意義教學(xué)，等號(hào)則被一筆帶過(guò)，以致在后續(xù)的學(xué)習(xí)中，學(xué)生更多的是在運(yùn)算中接觸等號(hào)，從而只關(guān)注了等號(hào)的算術(shù)意義。

2.實(shí)踐：重設(shè)情境，初步感受等號(hào)的關(guān)系性

等號(hào)雖然在《比大小》一課，就表現(xiàn)了它的關(guān)系性，學(xué)生也易于接受這種數(shù)與數(shù)的表征關(guān)系，但在《加法的認(rèn)識(shí)》一課，才在表現(xiàn)形式上發(fā)展到算式與數(shù)，直接帶來(lái)了等號(hào)含義的變化。例如，如圖1所示，在這個(gè)例題的教學(xué)中，多數(shù)教師會(huì)通過(guò)動(dòng)畫(huà)或身體語(yǔ)言幫助學(xué)生理解加法的意義，即合并。眾所周知，加法的意義學(xué)生在幼兒園甚至更早便已完全理解了。因此，不妨在這節(jié)加法課里，重整問(wèn)題情境。

根據(jù)加法和等號(hào)的本質(zhì)含義，教師可以借助比大小來(lái)幫助學(xué)生初步感受等號(hào)的關(guān)系性，改編如圖2所示。具體如下：先讓學(xué)生比較誰(shuí)的氣球多？再追問(wèn)：“怎樣才能讓兩個(gè)小丑的氣球數(shù)量一樣多？”根據(jù)學(xué)生回答“再加1個(gè)”后，教師可繼續(xù)追問(wèn)：“你是怎么知道丁丁和冬冬的氣球一樣多的？”

在這個(gè)過(guò)程中，學(xué)生先在3和4的大小比較中建立了關(guān)系，而后又在左邊的數(shù)量與右邊的數(shù)量是相等的關(guān)系中，理解了“3+1=4”，明白了算式與數(shù)其實(shí)也是在比較中得出的結(jié)果，從而感受到了“=”的關(guān)系平衡。

二、數(shù)學(xué)實(shí)驗(yàn)，豐富等號(hào)“平衡性”體驗(yàn)

一年級(jí)的小學(xué)生認(rèn)為，等號(hào)就意味著后面是答案，忽略了等號(hào)的關(guān)系性質(zhì)。因此，教師可以借助生活中喜聞樂(lè)見(jiàn)的原型，通過(guò)豐富的實(shí)驗(yàn)活動(dòng)，增強(qiáng)學(xué)生對(duì)等號(hào)平衡性的體驗(yàn)，促進(jìn)其對(duì)等號(hào)關(guān)系性的理解。

例如，數(shù)字天平（見(jiàn)圖3）是基于生活中蹺蹺板這一原型的數(shù)學(xué)學(xué)習(xí)工具，教師可以借助蹺蹺板的平衡經(jīng)驗(yàn)幫助學(xué)生理解等號(hào)兩邊的平衡性。數(shù)字天平的兩邊各有數(shù)字1～10、掛鉤和多塊相同的重量板，在相應(yīng)的數(shù)字掛鉤上掛重量板就對(duì)應(yīng)數(shù)字幾。

1.蹺蹺板：激活平衡經(jīng)驗(yàn)

在教學(xué)中，教師可以蹺蹺板作為引入，讓學(xué)生暢談蹺蹺板的游戲經(jīng)歷，通過(guò)生活中的原型，激活學(xué)生平衡的經(jīng)驗(yàn)，從而引入數(shù)字天平，讓學(xué)生明白當(dāng)數(shù)字天平兩邊一樣時(shí)，天平就會(huì)平平的，保持平衡狀態(tài)。

2.數(shù)字天平：多層推進(jìn)平衡感受

這是實(shí)驗(yàn)的重要環(huán)節(jié)。學(xué)生將在多重活動(dòng)中學(xué)會(huì)用等式來(lái)表征平衡。

第一步，給學(xué)生兩塊重量板，讓學(xué)生感受數(shù)與數(shù)的平衡。在學(xué)生初步體驗(yàn)數(shù)字天平玩法的同時(shí)，教師在教學(xué)時(shí)要遵循由不平衡的“﹥”或“﹤”到平衡的“=”的順序。同時(shí)，讓學(xué)生及時(shí)記錄天平的平衡狀態(tài)，如“4﹥3”“3﹤5”，再到“5=5”等。第二步，給學(xué)生三塊重量板，讓學(xué)生體驗(yàn)算式與數(shù)的平衡。在這個(gè)過(guò)程中，教師要注意兩種形式的變化，即算式在左數(shù)在右，算式在右數(shù)在左，并用算式來(lái)表示。第三步，給學(xué)生四塊或更多的重量板，讓學(xué)生體驗(yàn)算式與算式的平衡，并用算式表示。學(xué)生在參與制造平衡的數(shù)學(xué)實(shí)驗(yàn)中，積累了豐富的活動(dòng)經(jīng)驗(yàn)，并構(gòu)建了初步的平衡表象。

3.圖示天平：建立平衡模型

以數(shù)字天平實(shí)驗(yàn)為支撐，讓學(xué)生根據(jù)圖示天平表示出天平兩邊的平衡狀態(tài)，寫(xiě)出相應(yīng)的等式。從數(shù)到式子，再到圖形或符號(hào)，在列出等式的過(guò)程中，學(xué)生會(huì)不斷地進(jìn)行符號(hào)化的表征，鞏固等號(hào)兩邊的平衡關(guān)系。

三、建立聯(lián)系，突破等號(hào)“可逆性”

在現(xiàn)行的人教版低年級(jí)教材中，編者已有意識(shí)地在不同階段的練習(xí)中分散編排關(guān)于等號(hào)性質(zhì)的習(xí)題，逐步滲透、培養(yǎng)代數(shù)思維。

1.教材：滲透少而散

教材中對(duì)顯性的素材滲透少而散，第一次出現(xiàn)數(shù)與式的比較是在《10的加減法》后。但較教材之前，由浙江教育出版社出版、浙江省基礎(chǔ)教育課程教材開(kāi)發(fā)研究中心編寫(xiě)的《數(shù)學(xué)課堂作業(yè)本》比教材出現(xiàn)的早，在《0的加減法》后就出現(xiàn)了算式與算式之間的大小比較;《口算訓(xùn)練》則出現(xiàn)的時(shí)間更早，難度更高，剛學(xué)習(xí)了《5的加減法》就帶來(lái)了形如“2=□-3”的習(xí)題，給教學(xué)帶來(lái)更大的挑戰(zhàn)。因此，面對(duì)教材和習(xí)題的不同步，教師要挖掘教材中的隱性素材，為學(xué)生正確理解等號(hào)搭建平臺(tái)。

2.實(shí)踐：挖掘隱性素材

（1）在比較中搭起理解的橋梁

在習(xí)題中，算式與數(shù)、算式與算式的連線(xiàn)題就是等號(hào)關(guān)系性理解的隱性素材。如下習(xí)題，在教學(xué)中我們只要比平常多問(wèn)幾遍“為什么要這么連，還可以怎么表示”，讓學(xué)生在“獨(dú)立連線(xiàn)—解釋原因—等號(hào)連接”三個(gè)步驟的教學(xué)中，感悟到等號(hào)就像連的線(xiàn)用來(lái)描述兩個(gè)算式或算式與數(shù)的等價(jià)關(guān)系一樣，因?yàn)榈葍r(jià)所以相連。

（2）突出互逆運(yùn)算

等號(hào)作為關(guān)系符號(hào)，還具有可逆性。在一年級(jí)教材里，對(duì)于數(shù)的加減法，除了以“合并”引入加法，“取走”引入減法外，還用數(shù)的分解與組合模型來(lái)表示加減。從數(shù)的分成和組成，到加法和減法的運(yùn)算，都以四個(gè)等式的形式同時(shí)呈現(xiàn)，這些都有助于學(xué)生認(rèn)識(shí)到加法和減法運(yùn)算的互逆關(guān)系。互逆運(yùn)算的同時(shí)呈現(xiàn)，有利于學(xué)生看到運(yùn)算之間的關(guān)系，也有利于學(xué)生認(rèn)識(shí)等號(hào)的關(guān)系性。這樣的滲透和準(zhǔn)備，大大方便了簡(jiǎn)易方程的解法。

四、變換形式，多維度建構(gòu)等號(hào)“結(jié)構(gòu)性”

在課堂教學(xué)中，教師要常新、善變，通過(guò)原題目延伸出更多具有相關(guān)性、相似性的新問(wèn)題。

1.等式變形：變化中明確本質(zhì)

低年級(jí)學(xué)生由于受年齡和思維特點(diǎn)的影響，會(huì)覺(jué)得習(xí)題呈現(xiàn)方式的改變有一定的難度。如4+3=□+□，學(xué)生往往就在第1個(gè)方框填7，后一個(gè)方框隨便填。因此，在變換等式的形式中，讓學(xué)生在結(jié)構(gòu)中明確關(guān)系就很有必要。

在教學(xué)中，教師可以讓學(xué)生多接觸結(jié)果在左的等式結(jié)構(gòu)，如A=□+□，A=□+□-□等，從而幫助學(xué)生打破結(jié)果一定在等號(hào)右邊的觀念。同時(shí)，教師也可以讓學(xué)生多接觸算式與算式的等式結(jié)構(gòu)，如□+□=□+□等，幫助學(xué)生建立把兩個(gè)算式看作一個(gè)整體的概念。通過(guò)變式訓(xùn)練，學(xué)生在不斷進(jìn)行概括和比較中會(huì)提高對(duì)等式的理解。

2.圖形等式：符號(hào)化抽象出本質(zhì)

張?zhí)煨⒔淌谡J(rèn)為，要讓學(xué)生真正理解等號(hào)，需要學(xué)生形成把等式看作一個(gè)整體結(jié)構(gòu)的觀念，特別是讓圖形參與到計(jì)算過(guò)程中去。

例如，已知○+□=5， □+△=8，? ○+□+△=10，

則○=（? ?），□=（? ? ），△=（? ? ）。

比較直觀的方法，就是在解題中將前兩個(gè)算式看作一個(gè)整體來(lái)變形處理，再運(yùn)用代入法代入到第3個(gè)算式中，求出第3個(gè)圖形代表幾。具體為 +△=10，用5代替○+□，求出△=5。同理，也可將第2個(gè)算式代入第3個(gè)算式中求出○。在推算的過(guò)程中，學(xué)生會(huì)理解等號(hào)表達(dá)的是圖形與數(shù)之間的關(guān)系。

鄭毓信教授在探討小學(xué)數(shù)學(xué)教學(xué)的主要改革方向時(shí)提到，應(yīng)當(dāng)以“代數(shù)思維”作為小學(xué)算術(shù)教學(xué)的基本指導(dǎo)思想。教師作為學(xué)生發(fā)展路上的引路人，在整個(gè)算術(shù)教學(xué)中，都應(yīng)充分挖掘小學(xué)數(shù)學(xué)教材中代數(shù)思維的“雛形”，讓學(xué)生學(xué)會(huì)用代數(shù)思維思考算術(shù)和問(wèn)題，讓小學(xué)數(shù)學(xué)的算術(shù)教學(xué)也“居高臨下”。

【參考文獻(xiàn)】

中華人民共和國(guó)教育部.全日制義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[S].北京：北京師范大學(xué)出版社，2011.