以主題任務驅動數學融合學習

劉佳 嚴育洪

摘要：在數學教學中，可以尋找學習情境之間的聯系以及學習方式之間的聯系，把一個單元的知識甚至不同單元的知識圍繞一個主題融合成新的學習單元。西方有一句浪漫的諺語：“你在的時候你是全世界;你不在的時候，全世界是你”。借用在數學教學中，可以擴展為“數學你在的時候，你是全世界;數學你不在的時候，全世界是你”。其意為在數學課內，數學應該與“全世界”緊密相連;在數學課外，我們不僅要從“全世界”中看到數學，還應該通過數學指向其他學科知識的融合。

關鍵詞：主題任務驅動;小學教學;融合學習;學習活動

查理·芒格說：“他的智慧，來源于他的‘思想格柵’。在這里面，每一塊豎的木板，就可以看作是一個知識領域，而每一條橫木板，就是知識領域之間的聯系，它串聯起了兩個不同的領域。”

同樣，在教學中，我們也可以尋找這樣的“思想格柵”，把同一領域的各個知識甚至不同領域的各種知識橫向融合起來，創造新的學習主題，創造新的學習任務，創造新的學習單元，創造新的學習教材。

華東師范大學崔允廓教授倡導大單元備課以提升教學設計的站位：“一個單元就是一個完整的學習故事，就是一種課程，或者說微課程。譬如語文教材中的一個單元主題下的四篇課文，如果不是一個完整的學習方案，沒有學習任務的驅動，就只是內容單位，不是我講的單元概念。”

在數學教學中，我們可以不再局限于尋找學習知識之間的聯系，還可以尋找學習情境之間的聯系以及學習方式之間的聯系，把一個單元的知識甚至不同單元的知識圍繞一個主題，融合成新的學習單元。

（一）“對比式”融合學習

一些容易混淆的概念在單個教學的時候，因為對象比較“專一”，學生思維不會發生混亂，此時教學的即時效果往往很好。但很多時候，這只是一種表面現象，因為等到把另外一個似是而非的數學概念放在一起的時候，學生的思維有時候就會產生困惑。對此，比較著學、融合著學是解決這一問題的有效策略，這樣可以在第一時間內暴露學生的問題，在且行且思中逐步明晰概念。

例如，“面積”常常與“周長”糾纏不清，而教材在教學“面積”的時候并不沒有結合“周長”進行辨析。對此，我們采取了帶著“周長”教“面積”的融合策略，組建了綜合性學習新單元。

課首，教師把一個長方形變成了平行四邊形，讓學生發現圖形的周長相等，但面積卻越來越小，從而改變了學生開始所持有的“周長相等的圖形面積也相等”的錯誤想法，有效地使學生注意到了“面積”與“周長”所表示的不同意義。

在練習環節，教師又進一步引導學生思考（如圖1），在解答原有題目之后，讓學生繼續觀察其中的第一個圖形和第三個圖形，讓學生發現“面積相等但周長不相等”，與課首發現的“周長相等但面積不相等”相比較后形成完整的認識，再次感受到周長與面積意義的不同。

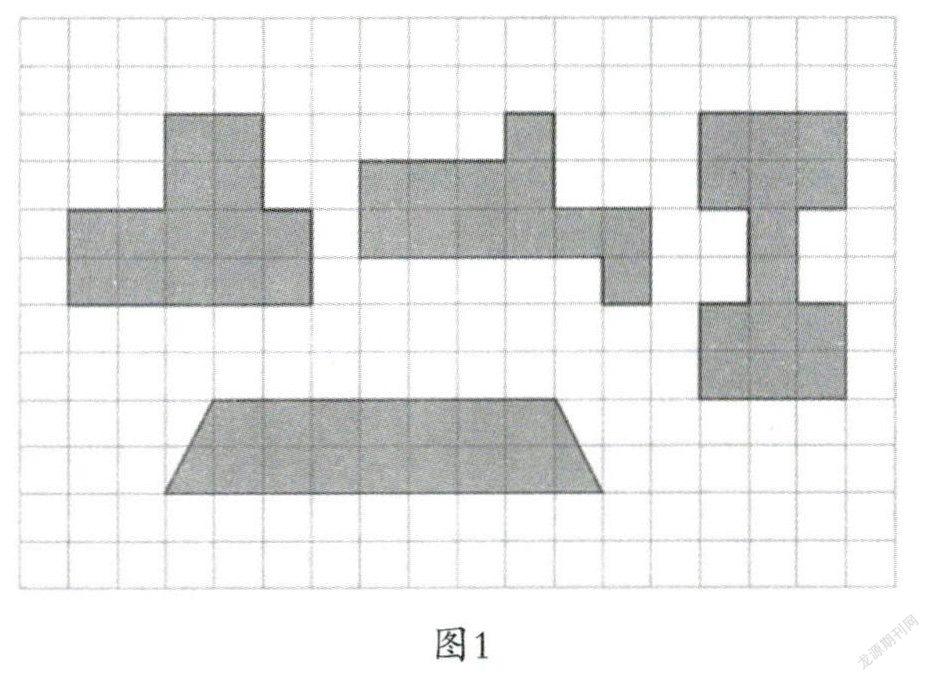
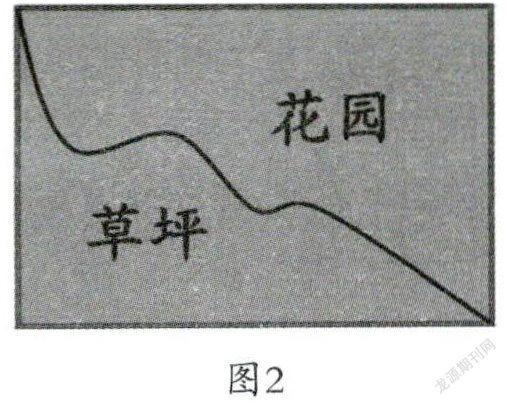
隨后，教師又設計了“畫一條線，把長方形分成兩個圖形，要求新得到的兩個圖形周長相等”的探究任務。從最初畫對角線到過中心點畫直線，直至在對角之間畫曲線（如圖2），學生的思維慢慢從關注面積而分成兩個相同的圖形中跳出來，最終能夠直接抓住周長的意義來尋找更多的答案。

繼而，教師又設計了“兩根繩子分別長22m和24m，分別圍成邊長是整米數的長方形，哪根繩子圍出的長方形面積大”的探究任務。這樣，促成了“面積”與“周長”的融合教學，教師還趁熱打鐵，鏈接到五年級的“用一一列舉的策略解決問題”一課（如圖3），提前整合到一個學習大單元之中，這樣的教學更具針對性和時效性。

認知心理學研究表明，碎片化學習內容的可辨識度比較低，既不利于學生的記憶，也不利于學生的理解。而“比較著學”這種融合學習，可以很好地將學習內容進行結構化設計，顯著提高內容的可辨識度，有利于學生在感知、理解、辨識的基礎上進行數學模型和數學模式的建構。

例如，有一位學生就對“時間、速度、路程”數量之間的關系設計了富有創造性的造型（如圖4），讓大家形象化地看到了它們之間的關聯。

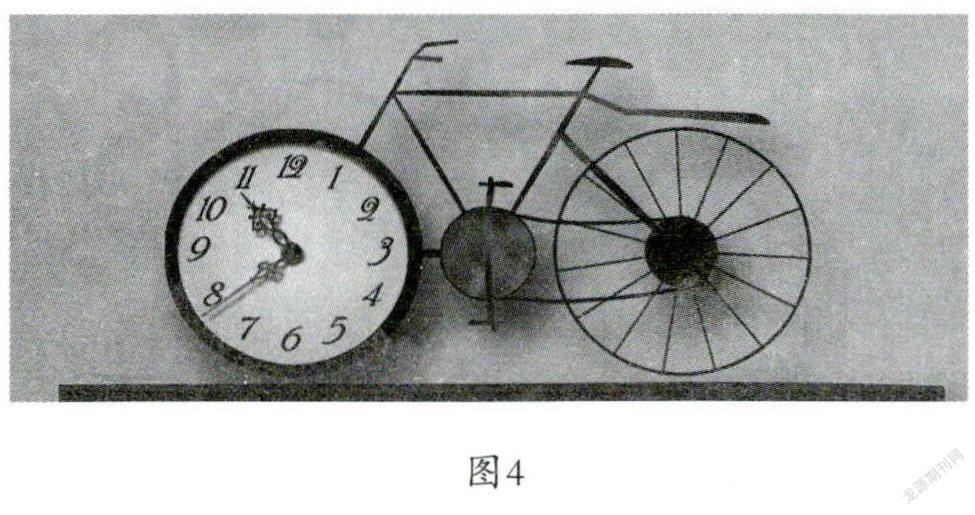
（二）“創研式”融合學習

在任務驅動學習中，我們可以設計知識的研發任務，引導學生從概念出發，根據知識之間的關系不斷創造出新的知識，或者把分散于不同單元的知識融合在一起進行整體化理解與記憶。

例如，除法的知識、分數的知識、比的知識，雖然身處不同年級、不同單元之中，但教p幣只需在每個單元教學的第一節課溝通了它們之間的關系，后續知識的學習中就可以讓學生成為“創客”，由“商不變規律”研發出“分數的基本性質”和“比的基本性質”（如圖5），這樣的課就成了“創課”，學生完全有能力去設計和當“小老師”。

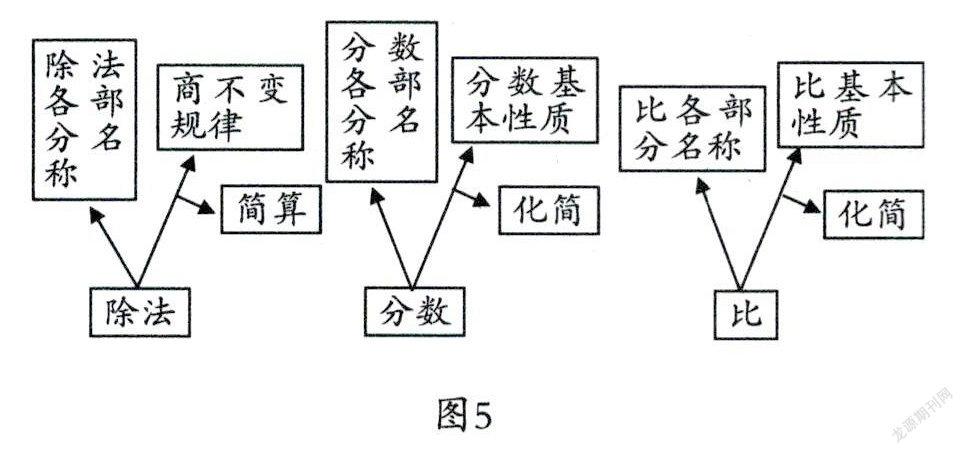
更重要的是，在知識的研發中，學生會自覺發現問題，最終明白“為何商不變規律稱之為規律”，是因為它是上位知識，由它推導出了“分數的基本性質”和“比的基本性質”。當學生有了這樣更深刻的理解，就會呈現這樣的知識譜系圖（如圖6）。

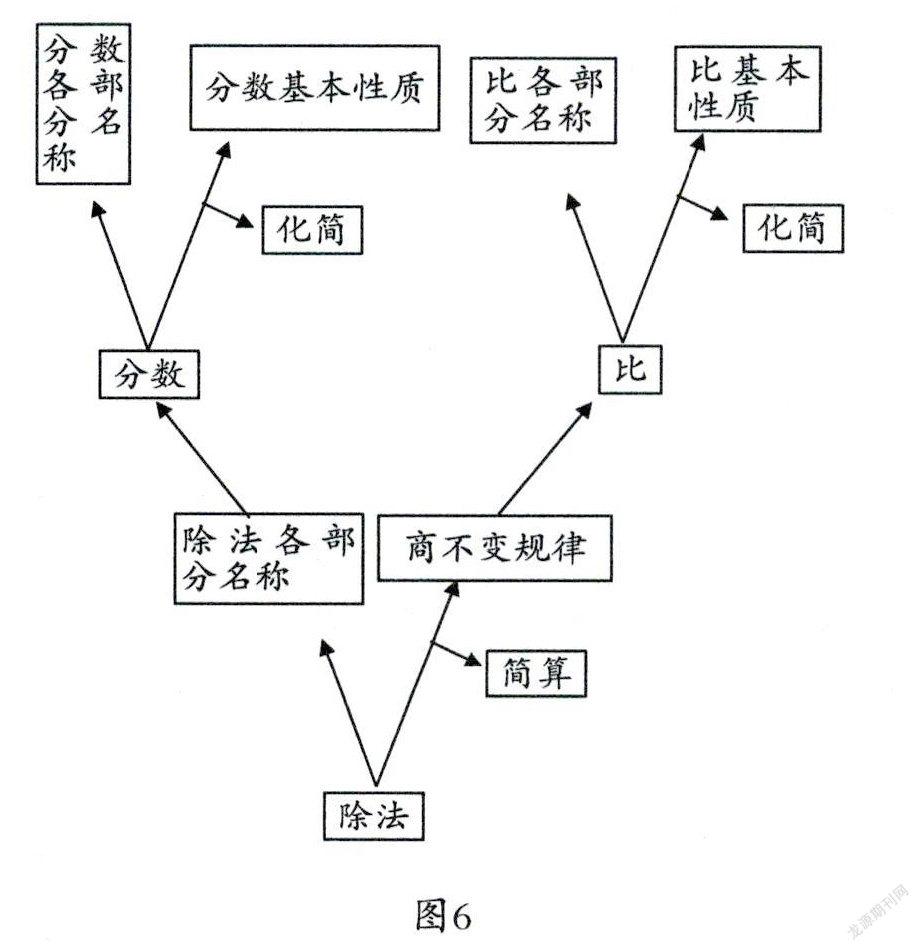
當然，我們也可以“后發制人”，通過知識回顧，引導學生尋找知識的血緣關系，重新組建成知識融合的學習大單元。此時，學生具備了知識的全景意識，看到的就不再是一棵棵“知識樹”，而是一片“知識林”。

（三）“挖井式”融合學習

弗賴登塔爾認為，數學化分橫向數學化和縱向數學化。在任務驅動學習中，我們可以將橫向數學化和縱向數學化融合起來，設計結合現實生活的挑戰性任務不斷深挖知識，實現學生對數學的深度學習。其中，一旦學生的深挖觸及到其它單元中的知識，此時的學習將開啟新單元，展現新氣象。

例如，學生在學習了“長方體和正方體的體積計算”之后，我們通過不斷變換情境和條件，層層設阻，使得學生的探究層層深入。

第一步：設計“如何計算不規則的橡皮泥的體積”的延伸性任務。學生想到了捏壓成長方體或正方體“等積變形”的轉化方法。

第二步：把橡皮泥換成石頭。學生在捏壓方法行不通的情形下，想到了排水法，把石頭浸入量杯后看所上升的水的體積。

第三步：把量杯換成長方體容器。學生同樣可以使用排水法，但需要事先測量長方體中原有水的長、寬、高以及浸入石頭后的水的高，通過計算得到石頭的體積。

第四步：把工具改成長方體容器和量杯。這時有學生想到了在長方體容器中裝滿水，浸入石頭，用量杯測量溢出的水的體積。

第五步：只給學生一個圓柱體容器。此時，所需的知識自然鏈接到了與“圓柱的體積計算”相關的下一冊教材的新單元教學內容，留給了學生新的學習期待。

第六步：既沒有量杯也沒有別的容器，或石頭無法放進容器，只有一塊規則的長方體石頭。這時，可引導學生通過稱重的方法間接求出不規則石頭的體積，其原理不僅“跨界”到了正比例的知識，還“跨界”到了中學所學的物理知識，后一種“不求甚解”可以讓學生帶著疑問走人中學物理的學習。

高斯說：“我們需要的是想法，不是符號。”數學不只是計算、測量和公式的應用，它更是一個充滿變化和新發現、新發明的領域。隨著上述挑戰性任務“戰線”的拉長和加深，學生思維的“觸角”也不斷延長和深入，伸向四面八方，尋求和融合更多的本學科知識甚至是外學科知識，獲得更多的新發現和新發明。如此情境下的練習功能就有了衍生性，它不再是單純的練習，還產生了新的學習，這是挑戰性任務生發出來的強勁的學習驅動力。

（四）“穿越式”融合學習

在教學中，如果我們在設計任務情境時，能夠沿用學生感興趣的已有知識特別是不同領域知識的情境，就可能會勾起學生對“往事的美好回憶”。此時的學習可能會有一種穿越感，也可能會有一種親切感和新奇感。這樣，傳統的知識單元之間可能就不再界線分明，知識也可能得以融合。

例如，當學生學完四年級的“可能性”（如圖7）這一課之后，到了五年級，我們就借用這個情境進一步設計游戲任務：在每個球上寫上一個數，讓學生任意摸出兩個球，如果兩個球上數的和是奇數，就可贏得一份獎品。以此替代五年級“和的奇偶性”的例題（女口圖8）。可以說，學生更喜歡從玩中學，能贏得獎品也增強了學生學習的趣味性。

為了能讓游戲具有戲劇性，也為了能激發學生主動探究的積極性，我們一開始寫的都是偶數，學生在“總是贏不了”的情境中自覺思考“為什么”。學生在最終的發現問題中獲得了“偶數+偶數=偶數”的結論。接著，我們讓學生自己修改游戲規則，有的學生提出都放人寫著奇數的球，在其他學生的反對中他們得到了“奇數+奇數=偶數”的結論。經過討論，大家一致認為必須同時放入寫著奇數的球和寫著偶數的球，這樣摸出的兩個球上數的和才有可能是奇數。在活動中，學生除了能發現“奇數+偶數=奇數”的結論，還能發現“摸出的兩個球上數的和是偶數比和是奇數的可能性大”這一拓展性知識。

上述情境把教材中單純的摸球變成了摸獎，游戲的刺激度得到了升級，學生的積極性也得到了升級，知識從四年級穿越到了五年級，也從統計與概率領域穿越到了數與代數領域，情境的延續帶給了學生“知識血肉相連”的學習一體感。

西方有一句浪漫的諺語：“你在的時候，你是全世界;你不在的時候，全世界是你。”如果我們浪漫地把“你”看成“數學”，那么前半句“數學你在的時候，你是全世界”，其意就是在數學課內，數學應該與“全世界”緊密相連，后半句“數學你不在的時候，全世界是你”，其意就是在數學課外，我們要從“全世界”中看到數學。而數學課外除了指向現實生活的融合，還應該指向其他學科知識的融合。

（一）“補充式”融合學習

數學教師無法弄明白和講清楚的其他學科知識，在補充教學時，可以邀請其他學科的教師來幫忙。

例如，在講解美術構圖中的“黃金比的應用”時，就不妨讓美術教師來講，這樣會更專業。如果時間允許，還可以專門配合上一節美術課。除此之外，“數學環節+美術環節”的融合還可以拓展成同一主題引領下的“數學課+美術課”的融合。

（二）“引發式”融合學習

用其他學科的知識或方式方法作為數學教學的導引，可以創設一種引人注目和引人人勝的任務效果，由此來驅動學生進行數學學習。

例如，在“軸對稱圖形”一課中，我們應該思考“如何讓美術教師走入數學課堂成為必要”。對此，我們可以讓美術教師閃亮登場，展示一技之長。在美術教師驚艷的教學活動中，在美術教師當場剪出美輪美奐的剪紙作品之時，學生也想學剪紙的滿腔熱情就被激發了。美術教師可以順勢告訴學生：“想學好剪紙藝術，先要學好軸對稱圖形的數學知識”。此時，“軸對稱圖形”知識的學習就成了學生完成剪紙任務的一種技術，課堂模式變成了“美術剪紙活動+數學軸對稱圖形知識+美術剪紙活動”的“夾心式”結構。這節融合了美術課的數學課，盡管數學依然是主體，美術只是引子，但仍有許多學生認為這節課的課題是“學剪紙”。當然，通過這節課，學生還不能完成較復雜的剪紙任務，教師順勢可以在課后組建剪紙興趣小組，讓有興趣的學生繼續深造。

（三）“情境式”融合學習

教師可以創設一種具有綜合性、感染性和挑戰性的生活情境，讓學生置身實際情境中去產生數學學習的需要。

例如，上述“軸對稱圖形”一課中，除了讓美術教師當場展示剪紙才藝來吸引學生的眼球，然后引入數學學習之外，我們還可以創設“過年”的情境。由于在布置環境時用到了美麗的剪紙，再由剪紙引到數學“軸對稱圖形”的學習，課堂模樣進一步變成了“過年+美術剪紙活動+數學軸對稱圖形知識+美術剪紙活動+過年”的“圓通式”結構。在這樣充滿喜氣的任務情境的渲染下，也有學生可能會認為這節課的課題是“過年”。

可以說，在這樣的情境融合和知識融合的課堂中，學生的學習必定是充滿喜悅之情的。如果這節課放在元旦前或春節前教學，情境效果會更好，而學生完成的剪紙作品還可以用來布置教室或家里的新年環境。

總之，知識的深度融合發展是一項系統性工程。在任務驅動的融合學習中，所設計的長線任務和長效任務，如同“放長線釣大魚”，要能夠釣到“大魚”，一是需要“水面”寬廣，也就是我們要開展有利于學習的大單元設計，二是需要引進“活水”，也就是我們要融合不同領域的知識設`計學習活動。