架起學生“數”與“形”的立交橋

趙長遠

摘要：學生在解決一些圖形問題時常常感覺有困難，而教師在平時的教學中比較重視學生抽象思維的培養，卻忽視了學生形象思維的發展。如何促進學生的思維與能力協同發展？最好的方法就是為學生搭起一座橋梁——“數形結合”。在教學過程中，教師應做個有心人，充分利用“一圖抵百語”的優勢，向學生滲透“數形結合”的思想，引領學生走進數學的神奇殿堂。

關鍵詞：抽象思維;形象思維;數形結合

邏輯思維的始祖亞里士多德說過：“心靈沒有意象就永遠不能思考。”數學知識本身具有很強的抽象性。數學是什么？18世紀，恩格斯在考察了整個數學發展的歷史后指出：“純數學是以現實世界的空間形式和數量關系這一非常現實的材料為對象的。”因此，教師在教學中必須突出數形結合思想這一數學的精髓和靈魂。

聯系平時的課堂，以及對學生進行的調查，我發現目前有相當一部分學生在解決一些圖形問題時常常感覺有困難，而我們教師在平時的教學中，比較重視學生抽象思維的培養，卻忽視了學生形象思維的發展。那么，如何促進學生的思維與能力協同發展？

一、數形結合——培養學生思維的靈活性

教師在引導學生解決問題的過程中，要善于利用“數形結合”的方法，啟發學生思維，調動學生思維的積極性，以培養學生思維的靈活性。

在學生用通分的方法算出第①小題后，教師可以啟發學生思考：還有沒有更簡便的方法？如果學生一時想不出，我們可以這樣巧妙地引入：一塊菜地，它的? ? 用來種青菜，它的? ? ?用來種蘿卜， 用來種土豆，它的? ? ? 用來種西紅柿，這四種蔬菜的面積一共占這塊地的幾分之幾？

教師引導學生想到借助畫圖來理解，配合圖形進行分圖巧算，充分利用“數形結合”，將學生的思維引向深入。可以先畫一個正方形，這個正方形的一半就是它的? ? ，剩下長方形的一半就是它的? ? ?，再把剩下的正方形平均分成兩份，一份就是大正方形的? ? ?……

這一過程絕不是簡單的模仿和記憶，而是在將數字的計算與圖形的分割巧妙結合之后，將抽象的純數學知識轉化為具體形象的、便于學生理解的表象，從而將數與形有機地結合起來，發展了學生思維的靈活性。

二、數形結合——培養學生思維的深刻性

思維的深刻性是小學生思維品質的基礎。教師在平時的教學中，要善于引導學生依據問題與已知條件的內在聯系，由數想形，以形思數，把抽象的問題直觀化，具體化，引領學生把握數學問題的本質，使學生不僅知其然，而且知其所以然，從而達到培養學生思維深刻性的目的。

例：小軍收集了一些畫片，他拿出畫片的一半還多3張送給小明，自己還剩25張。小軍原來有多少張畫片？

學生通過看圖，一目了然地看出題中隱藏的數量關系，實際上“拿出畫片的一半還多3張”也就是：先給一半，再送3張。這時還剩25張，學生很自然地理解了解決問題的方法：先用（25+3），得到總張數的一半，再乘2，得到小軍原來有多少張畫片。

當然，有的老師通過實物演示，也達到了很好的效果：讓學生親自到前面拿出畫片的一半，再抽出3張，這時告訴學生還剩25張，學生也很容易倒過來進行推想。

其實不管是畫圖演示，還是通過實物演示，都是從數學的感性材料出發，通過邏輯思維，揭示數與形的本質特征，透過表面揭示問題本質。

三、數形結合——培養學生思維的獨創性

在面對一些新問題時，能采用相應的對策，思維不循常規，并且能采用獨特、新穎的解題方法，這就是思維的獨創性。在平時的教學中，我們應積極引導學生對題中的數量關系、問題的結構特點進行探索，尋求規律，把數與具體圖形或實物結合起來，幫助學生借助具體形象進行抽象思維，從而培養學生思維的創造性。

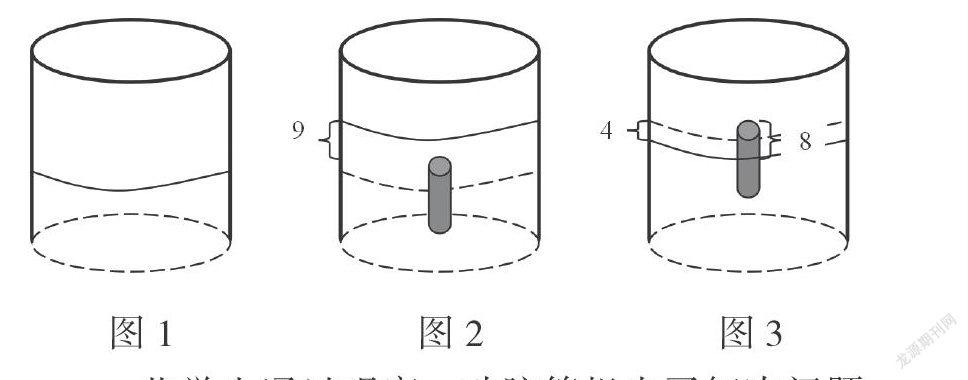
例：在一個圓柱形儲水桶里，把一段半徑是5厘米的圓鋼全部放入水中，水面就上升9厘米;把圓鋼豎著拉出水面8厘米后，水面就下降4厘米。求圓鋼的體積。

【分析與思考】仔細讀題，題目的意思還真是有點難理解。為了幫助學生理解題意，我一共畫了三幅圖：首先，在一個圓柱形儲水桶中，原來有一些水（圖1）。接著，將一個底面半徑為5厘米的圓鋼全部放入水中，水面上升了9厘米，引導學生觀察思考：圓鋼的體積就相當于上升的水的體積。最后，又出示了第三幅圖，將圓鋼拉出8厘米，水面下降了4厘米，說明拉出的一部分圓鋼體積就等于下降的水的體積。引導學生仔細觀察這三幅圖。并思考：可以從何處入手呢？

一些學生通過觀察，動腦筋想出了解決問題的辦法：先求出拉出水面的圓鋼的體積，也就是下降了4厘米水的體積，用5×5×3.14×8=628（立方厘米）;再求出圓柱形儲水桶的底面積，用628÷4=157（平方厘米）;最后求上升了9厘米水的體積，也就是整個圓鋼的體積，用157×9=1413（立方厘米）。

我表揚了這些學生善于觀察、善于思考，同時激發學生思考：解決這一問題，你還有更簡便的方法嗎？經過思考，幾位學生激動地舉起了小手。A同學發現了這樣的方法：圓鋼拉出水面8厘米，水面就下降了4厘米，8厘米正好是4厘米的2倍;而將圓鋼全部放入水中時，水面上升了9厘米，說明圓鋼的高度是9厘米的2倍，也就是18厘米！那求圓鋼的體積就很簡單了：5×5×3.14×18=1413（立方厘米）。真不錯！

愛動腦筋的B同學想到：我們可以將圓鋼看作兩段，水面以上的為一段，水面以下的為一段。結合圖2，這兩部分都沉入水中時，水面上升9厘米;一部分圓鋼到了水上，水面就下降了4厘米，那水下的那部分圓鋼，就相當于（9-4）=5厘米水的體積。根據4：5的關系，用8÷4×5=10（厘米），求出圓鋼在水面以下的高度，再用（8+10）×5×5×3.14=1413（立方厘米），就可以求出圓鋼的體積。

也許受剛才同學的啟發，C同學又想到一種方法：求出水面以上的圓鋼體積，因為4厘米占9厘米的? ? ，說明露在水面以上的圓鋼體積也是占整個圓鋼體積的? ? ，可以用5×5×3.14×8÷? ?=1413（立方厘米）。

課上，不斷閃爍的學生創新思維的火花，來自于教師的巧妙引導與激發，更來自于教師為學生構建的橋梁——數形結合。

四、數形結合——培養學生的空間想象力

發展學生的空間觀念包括發展學生的空間想象能力、空間思維能力及操作實踐能力。當前學生的空間觀念有待加強，發展學生的空間觀念，最有效的途徑是“數形結合”，讓學生學會畫圖，逐步培養其空間想象力。

例如，六年級上冊長方體和正方體單元，有這樣一道思考題：

一個正方體，棱長4厘米，在它的表面涂上紅色，每個面等距離地切三刀，平均分成64塊小正方體。問：

（1）三個面涂紅色的小正方體有多少塊？

（2）兩個面涂紅色的小正方體有多少塊？

（3）一個面涂紅色的小正方體有多少塊？

學生通過觀察、比較、討論、分析，得出一致結論：（1）三個面涂紅色的小正方體在頂點處，共8塊;（2）兩個面涂紅色的小正方體在每條棱的中間處，共12×2=24塊;（3）一個面涂紅色的小正方體在每個面的中間處，共6×4=24塊。學生已經能夠初步理解并獨立解決這道思考題。

不過，為了進一步發展學生的空間觀念和想象能力，我又設計了一道相似的拓展練習題：在長5厘米、寬4厘米、高3厘米的長方體木塊表面涂上紅色，然后切成若干個棱長是1厘米的小正方體。

（1）三面、兩面、一面涂色的小正方體各有多少塊？

（2）表面不涂色的小正方體有多少塊？

學生讀完題目，都感覺到這個問題比較難，有些學生已經自覺地在紙上涂涂畫畫，我立刻將這些學生的行為加以表揚，放大。解決這樣的問題，直接在頭腦里思考是比較困難的，而把題中的圖形畫下來，就可以化抽象為具體，再加以觀察，分析，就可以化難為易，逐步解決問題。

學生在畫出立體圖后，通過仔細觀察后得出：

（1）三面涂色的小正方體還是8塊（在8個頂點處）;兩面涂色的小正方體在每條棱的中間，就可以用：（3+2+1）×4=24塊;一面涂色的小正方體在每個面中間，可以用（6+3+2）×2=22塊。

（2）表面不涂色的小正方體在哪里呢？有學生想到了在中間，但想不清楚是幾塊，怎么辦呢？學生經過激烈的小組討論、全班交流后，得出了不同的方法：

①用總塊數減去三面、兩面、一面涂色小正方體的塊數，就可以得到中間沒有涂色的小正方體的塊數。先用5×4×3=60塊，再用60-8-24-22=6塊。

②將長方體的長、寬、高各減去2，就得到里面的長、寬、高，再相乘，得到中間沒有涂色小正方體的塊數。用（5-2）×（4-2）×（3-2）=6塊。

這樣的問題，也許有些難度，但卻很好地激發了學生的思維。學生通過動手畫圖、動眼觀察、動腦思考，發展了空間想象力;更重要的是在這一學習思考的過程中，他們想到采用數形結合的思想來解決問題，那真是一種境界的提升。

早在1637年，著名的數學家笛卡爾就將相互對立的“數”與“形”統一起來，研究產生了“解析幾何”。如今，數形結合不僅是小學數學教材編排的一個重要特點，更是小學生解決問題常用的方法之一，同時又是一種數學的思想。在教學過程中，我們教師應做個有心人，充分利用“一圖抵百語”的優勢，向學生滲透“數形結合”的思想，引領學生走進數學的神奇殿堂。

（責任編輯：吳延甲）