《1.2.4平面與平面的位置關系(第一課時)》教學案例

方澤運

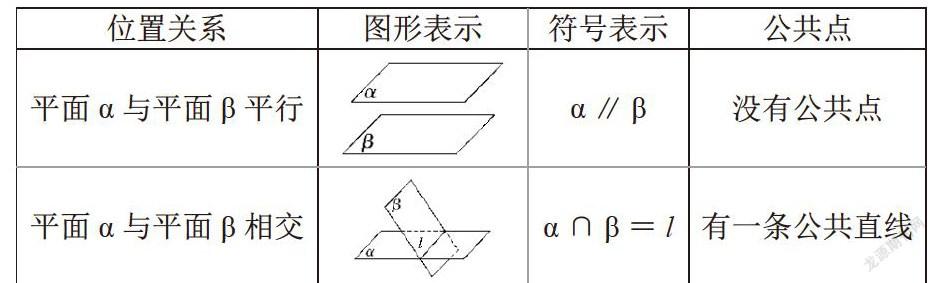
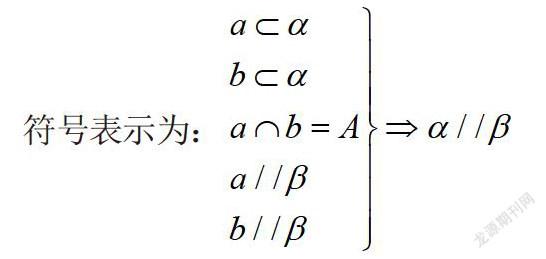
摘 要：依據《數學課程標準》中關于空間中平面和平面位置關系的教學要求，引導學生類比空間中線與線、線與面的位置關系學習，通過對教室內的地面、天花板面、墻壁等位置關系進行分析，組織學生展開討論。結合兩個平面公共點個數進行位置關系的分析，總結歸納，探究空間中兩個平面的具體位置關系，進一步尋找平面與平面平行的判定定理和性質定理，直觀感知，理論聯系實際，幫助學生提高探索分析問題的能力。

關鍵詞：平面;位置關系;教學案例

蘇教版普通高中課程標準試驗教科書必修2的《1.2.4平面和平面的位置關系》學習時，學生已經學習了空間線與線、線與面的位置關系，空間兩個平面的位置關系也是學生比較熟悉的，如教室的墻壁、地面、屋頂所在平面的位置關系，引導學生積極討論，進而根據兩個平面公共點的情況歸納出兩個平面的位置關系，進一步尋找平面與平面平行的判定和性質定理，于直觀感知中，鼓勵學生探索發現。

學情分析

學生已經學習了線與線和線與面的位置關系，空間兩個平面的位置關系也是學生比較熟悉的，如教室的墻壁、地面、屋頂所在平面的位置關系，引導學生討論，進而根據兩個平面公公共點的情況歸納出兩個平面的位置關系.進一步尋找平面與平面平行的判定和性質定理，于直觀感知中，鼓勵學生探索發現.

教材分析

兩個平面互相平行在學習“棱臺”定義時，對其就有所介紹，教學時可結合平面互相平行的定義，回顧棱柱、棱臺、圓柱、圓臺的概念，逐步推進直至發現判定定理.

對于兩個平行平面的性質定理的教學，要引導學生認真分析教材中提示的兩個問題，兩個平行平面內的線線關系，區分“異面和平行”，從而自然地引出兩個平面平行的性質定理及其證明與應用.

教學目標

1.理解并掌握兩個平面平行、兩個平面相交的定義，會畫平行或相交平面的空間圖形，并用符號語言表示.

2.通過探究空間兩個平面的位置關系以及平面與平面平行的判定與性質定理，明確數學概念的嚴謹性和科學性，培養學生運用數學思維分析解決問題的意識.

3.通過直觀感知、探究、思考、反思、完善，進一步培養學生空間想象能力、理性思維能力以及團隊合作創新能力。理論聯系實際，滲透數學核心素養.

教學重點

1.了解空間兩個平面的位置關系.

2.兩個平面平行的判定定理和性質定理及其應用.

教學難點

兩個平面平行的判定定理、性質定理及其應用.

教具準備

多媒體課件、長方體模型等.

課時安排1課時

教學過程

創設情景，引入新課

師：前面幾節課我們已經研究了空間兩條直線、直線和平面之間的位置關系，同時我們也掌握了空間直線和直線、直線和平面的各種位置關系的判定和性質，你覺得構成空間圖形的基本元素之間的哪種關系我們還沒有研究呢？

（生思考）

師：現在我們來探究空間兩個平面之間的位置關系。

（生思考）

師：數學無處不在，某學校宿舍里的雙層床（如圖所示），上鋪和下鋪的床板面就可抽象成兩個平面，爬梯所在面可抽象成一個平面.

問題1：床板所在的兩平面是什么位置關系？公共點有多少？

問題2：床板所在平面和爬梯所在平面是什么位置關系？公共點有多少？

（生探究后歸納）兩平面的位置關系：

合作探究，推進新課

探究空間兩個平面平行的判定定理

問題1：如果平面α內有一條直線a平行于平面β，那么α與β平行嗎？（不一定）

問題2：如果平面α內有兩條直線a，b平行于平面β，那么平面α與β平行嗎？

（不一定）那你認為怎樣才能判定兩平面平行？

師：同學們知道木工師傅是怎樣利用水平儀檢測桌面是否水平的嗎？這樣做的理論依據是什么？（生思考）

（多媒體慢鏡頭播放木工師傅利用水平儀檢測桌面是否水平的過程，組織學生觀察）

師：同學們能把木工師傅利用水平儀檢測桌面是否水平過程用自己的語言敘述出來嗎？

（生討論交流，師適時歸納，得出如下結論）

木工師傅將水平儀在桌面上交叉放置兩次，如果水平儀的氣泡兩次都在中央，就能判斷桌面是水平的.

師：木工師傅這樣做的原理是什么呢？

（生討論交流，抽象出兩平面平行的判定定理，板書定理）

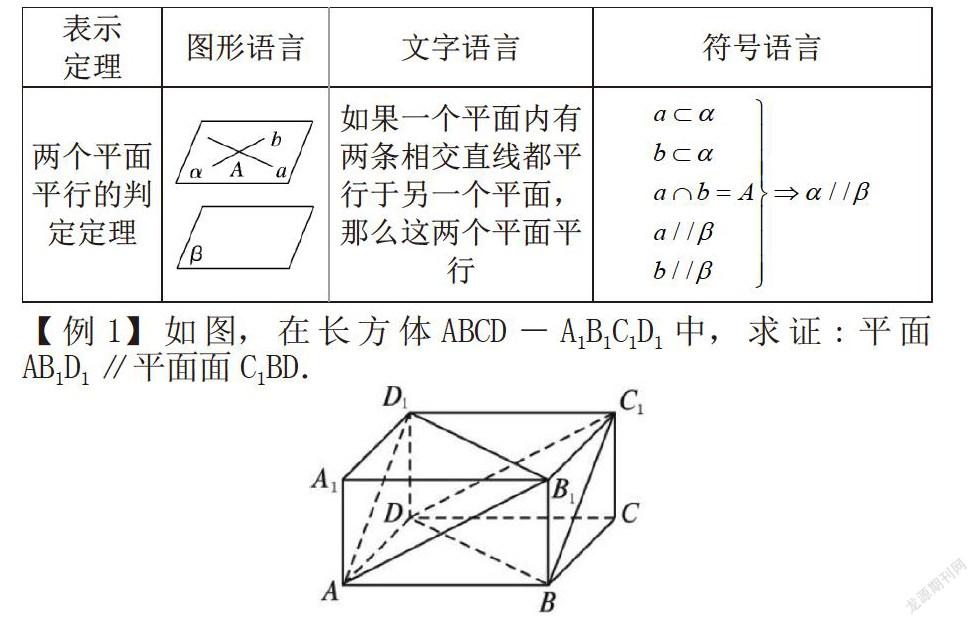
兩個平面平行的判定定理

如果一個平面內有兩條相交直線都平行于另一個平面，那么這兩個平面平行.簡述為“線面平行則面面平行”.

師：你能在長方體模型中借助于長方體的棱和面的位置關系來驗證上述結論的正確性嗎？

（生探究）

師：你能否用符號語言和圖形語言來表示上述定理呢？

（生討論，并動手畫圖歸納出如下結論）

【例1】如圖，在長方體ABCD-A1B1C1D1中，求證：平面AB1D1∥平面面C1BD.

師：根據你所學的知識，你認為要證明空間兩個平面平行，可以從哪些方面來考慮呢？

（生思考）

探究：證明空間兩個平面平行的方法有哪些？

（生討論，得出如下結論）

師：：證明空間兩個平面平行有以下兩種方法：

（1）定義法：根據定義，即如果兩個平面沒有公共點，那么這兩個平面平行.符號表示為α∩β=Φ則α∥β.

（2）平面與平面平行的判定定理：

如果一個平面內有兩條相交直線都平行于另一個平面，那么這兩個平面平行.簡述為“線面平行則面面平行”.可以用符號表示為：

師：你覺得對于例1用哪種方法證明比較方便呢？

生根據判定定理.

師：如何運用判定定理來證明呢，其關鍵是什么？

生只要證明一個平面內有兩條相交直線與另一個平面平行.

師：請同學們完成該題的證明，并和你的同桌交流你的證法.（板書）

探究兩個平面平行的性質

師：如果兩個平面平行，那么一個平面內的直線和另一個平面的位置關系是怎樣的呢？

生平行.

師：你能解釋一下嗎？

（生討論，結合兩平面平行的定義，給出如下解釋）

因為兩個平面平行，則這兩個平面沒有公共點，所以一個平面內的任意一條直線均和另一個平面沒有公共點，由線面平行的定義可知，這條直線和這個平面平行.

師：分別在兩個平面內的兩條直線的位置關系是怎樣的呢？

生因為兩個平面平行，所以它們沒有公共點.因此，分別在兩個平行平面內的兩條直線也沒有公共點，根據空間兩條直線的位置關系，可得分別在兩個平行平面內的兩條直線要么平行，要么異面.

師：怎樣才能在兩個平行平面內找到兩條互相平行的直線呢？

（生思考）

師：能否在教室里或在長方體中找到具體實例呢？

（生探究，并把自己的探究結果用文字語言敘述。）

（師適時歸納得出如下結論）

結論：如果兩個平行平面同時和第三個平面相交，那么它們的交線平行.

師：你能用你所學過的知識證明上述結論嗎？

（生思考）

探究：求證：如果兩個平行平面同時和第三個平面相交，那么它們的交線平行.

師：你能用符號語言和圖形語言表示上述問題的已知和求證嗎？

（生討論，歸納如下結論）

已知：α∥β，α∩γ=a，β∩γ=b.

求證：a∥b.

師：要證明空間兩條直線平行，可以從哪些方面來考慮呢？

（生討論，得出如下結論）

師：證明空間兩條直線平行的方法有以下幾種：

（1）根據兩條直線平行的定義：即在同一平面內，且沒有公共點;

（2）平行公理（公理4）即若a∥b，b∥c，則a∥c;

（3）根據直線和平面垂直的性質定理：即若a⊥α，b⊥α，則a∥b.

師：對于該題，你覺得用哪種方法證明比較簡單呢？

（生討論，并完成解答）

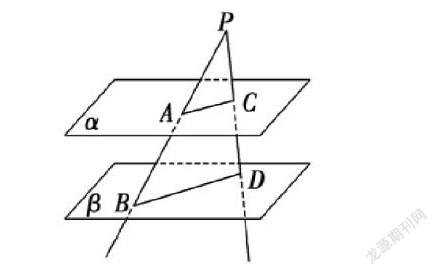
【例2】如圖，已知α∥β，點P是平面α，β外的一點（不在α與β之間），直線PB，PD分別與α，β相交于點A，B和C，D.

（1）求證：AC∥BD;

（2）已知PA=4，AB=5，PC=3，求PD的長.

（生分析圖形并寫出解答過程）

課堂練習，鞏固提升

課本第45頁練習題2、3、4.（視教學實際靈活安排）

課堂小結

師：請同學們總結一下本節課中所學的知識和運用的主要數學思想.

（生以交流的方式對本節課所學知識和思想方法加以總結）

1.空間兩個平面的位置關系有哪幾種？其分類的依據是什么？

2.兩個平面平行的判定方法有哪些？

3.兩個平面平行的性質定理及應用.

數學思想：類比轉化

布置作業

《課時作業本》第23-24頁.

板書設計

教學反思

在認真研讀教材和教學參考書，多次請教組內資深教師和骨干教師后，確定了1.2.4節第一課時的教學內容：空間中兩個平面位置關系的概念、表示方法，面面平行的判斷定理、性質定理及其應用。

新課程理念中倡導學生主動探索、動手實踐、合作交流。于是我在教學中主要關注學生的主體參與程度，引導學生經歷從具體實例抽象出數學概念的過程，通過對生活中教室架構、宿舍的雙層床鋪等實際模型的認識，學會將空間平面位置關系及判斷與性質的文字語言轉化為圖形語言和符號語言，注重數學思想潛移默化的滲透。

回顧整個課堂教學過程，準確把握教學重點、難點，各環節的安排基本合理，師生互動，探索發現過程流暢，教學中突出了學生對基本概念的理解及對基本思想的領悟，學生參與教學活動積極發言，上黑板練習正確，較好的完成了本節課的教學任務。

當然也有一些遺憾的地方，在平面與平面的判定定理的引入時，如果準備一個水平儀，課堂上讓學生自己實驗觀察水平儀的氣泡位置，進而判斷歸納出面面平行判定定理的內容，那樣也許會更精彩。其次，第一個例題給出后，學生明顯感覺吃力，表明對普通班學生而言難度有點大了。再者，課堂教學語言可以更精練些。在今后的工作中，我將認真改進不足，努力上進。

感謝學校開展教科研活動，給予我們年輕老師鍛煉和成長的機會，今后我將一如既往的向組內資深教師學習，向骨干教師學習，刻苦鉆研，努力使自己的業務水平上升到一個新的臺階。

參考文獻

[1]普通高中數學課程標準.人民教育出版社.

[2]普通高中數學課程標準實驗教科書.江蘇鳳凰教育出版社.

[3]普通高中數學教學參考書.江蘇鳳凰教育出版社.