對密碼安全性的研究

姚明　姚兵

摘? 要：利用新定義與標號理論，找到使得不同的圖模塊在一定條件下可相互轉換的關鍵點，給出圖模塊之間基于這一點變換所需要的可算法化的算法，得到圖模塊由點連結變成由邊連結的方法，為快速大規模構造圖形結構和方便實際應用在理論上有了依據。

關鍵詞：優美標號;全優美空間;邊有序全優美標號;邊有序全優美空間

中圖分類號：TN918.4;O157.5? ? ? ?文獻標識碼：A 文章編號：2096-4706（2019）23-0136-04

Research on the Security of Password

YAO Ming1，YAO Bing2，3

（1. Lanzhou Petrochemical Polytechnic，Lanzhou? 730060，China;

2.College of Mathematics and Information Science，Northwest Normal University，Lanzhou? 730070，China;

3.School of Electronics and Information Engineering，Lanzhou Jiaotong University，Lanzhou? 730070，China）

Abstract：By using the new definition and labelling theories，we find the key points that make different graph modules can be converted to each other under certain conditions，and give the algorithmic algorithm needed by the transformation between graph modules based on this point，and get the method that the graph module changes from point connection to edge connection，which provides a theoretical basis for fast and large-scale construction of graph structure and convenient practical application.

Keywords：graceful space;total graceful space;edge-ordered total graceful labellings;edge-ordered total graceful graphs space

0? 引? 言

基于一點的可算法化的結果能讓圖形結構方便實際應用，破譯困難，尤其是圖結構的靈活多變，能組合各種所需圖結構，為快速大規模構造圖形結構在理論上提供了保證;因需要基于一點變換而衍生的算法使密碼的安全性得到加強。邊有序全優美標號（edge-ordered total graceful labellings）、邊有序全優美空間的定義使得研究的結果指向優美樹猜想，這有助于探索優美樹問題，而優美樹的分解猜想成立則取決于猜想能夠被證明[1，2]，諸多的研究成果表明解決它仍很困難[3]，算法可為研究優美樹問題提供數理支撐。

1? 預備知識

若無特別聲明，文中論及的圖均指有限、無向、簡單連通圖，未定義的術語和符號可參見文獻[4]。為方便敘述，規定記號[m，n]={m，m+1，…，n}。

其中：整數n>m≥0。

F（G）為G的二部分圖空間[5]，設樹T∈F（G）有集合Ф（T）={g|g為T的正常標號}，一個正常標號g對任意的x，y∈V（T），有g（x）≠g（y）;

此外：∏（T）={g|g：V（T）∪E（T）→[m，n]}，且對任意的x，y∈V（T）∪E（T），有g（x）≠g（y），則g為圖T的一個正常的全標號。

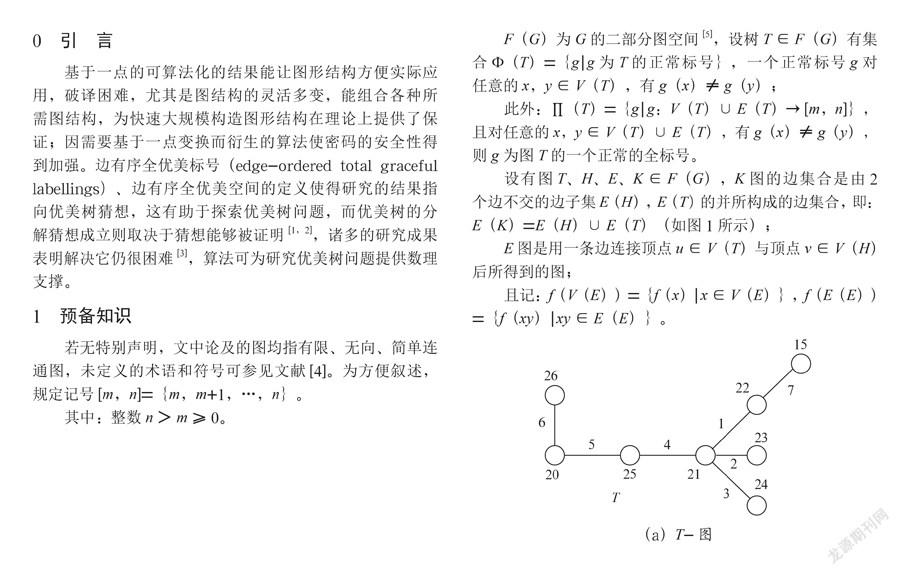
設有圖T、H、E、K∈F（G），K圖的邊集合是由2個邊不交的邊子集E（H），E（T）的并所構成的邊集合，即：E（K）=E（H）∪E（T）（如圖1所示）;

E圖是用一條邊連接頂點u∈V（T）與頂點v∈V（H）后所得到的圖;

且記：f（V（E））={f（x）|x∈V（E）}，f（E（E））={f（xy）|xy∈E（E）}。

（a）T-圖

（b）H-圖

定義1[6-8]：

設集合L（G）={f|f：V（G）→[0，p-1]，f∈Ф（G），G∈F}。

若：

（1）對任意的f∈L（G），使得uv∈E（G），滿足{f（uv）|uv∈E（G）}=[1，q];

（2）圖G的任何一個優美標號滿足f∈L（G）;

則稱L（G）為G的優美空間（graceful space），記為LGS（G）。

定義2[9，10]：

設圖G∈F有集合L（G）={g|g∈∏（G）}。

若：

（1）對任意的g∈L（G），使得uv∈E（G），滿足{f（uv）|uv∈E（G）}=[1，q];

（2）圖G的任何一個全優美標號滿足f∈L（G）;

則稱L（G）為G的全優美空間（total graceful space），記為LTGS（G）。

定義3：

設圖G∈F有f∈Λ（G）={f|f∈LTGS（G）};邊集合E（G）=E（H）∪E（T），E（H）∩E（T）=?。

若：

（1）對任意的（p，q）-圖H及圖T，使得uv∈E（H），xy∈E（T），滿足{f（xy）|xy∈E（T）}=[1，q]，{f（uv）|uv∈E（H）}=[q+1，2q];

（2）圖G的任何一個標號滿足f∈Λ（G）;

則稱f邊有序全優美標號，圖G為邊有序全優美圖，且記ΛEOTGL（G）={f|f為邊有序全優美標號}。

定義4：

設圖G有集合δ（G）={G|G∈F，G為邊有序全優美圖}。

若：

（1）對任意的圖F，T∈δ（G），總有F∪T∈δ（G）;

（2）任何一個圖G滿足G∈δ（G）;

則稱δ（G）為G的邊有序全優美圖空間（edge-ordered total graceful graphs space），記為δEOTGGS（G）。

2? 主要結果及證明

定理1：

設圖K∈F（G）有標號g∈∏（G），E（K）=E（H）∪E（T），H為（p，q）-圖;若對于u∈V（T），有點p+ q=M∈V（K），使得g（u）-g（M）=q，則g∈ΛEOTGL（K）。

證明：

設（p，q）-圖H有標號f∈LTGS（H），頂點集U={vi|i∈[1，s1]}，U ′={uj|j∈[1，t1]}，f（vi）>f（uj），f（vt1）=p+q;圖T有頂點n=p-1，頂點集為X={xi|i∈[1，s2]}，Y={yj|j∈[1，t2]}。

（1）令標號h∈∏（T）滿足：h（yj）=p+j，h（xi）=q-1+i;

不失一般性，可設h（yt1）=h（x1）+q-1;

由此推得：h（yt2-1）=h（x1）=q-2，h（yt2-2）=h（x1）+q-3，…，h（y1）=p+1;

注意到h（x1）=p，h（x2）=p-1;

因此h（yt2）=p+q-2，h（yt2-1）=p+q-3，h（yt2-2）= p+q-4，…，h（y1）=p+1;

此處h（yj）>h（xi）;

因此有h（E（T））={h（yj）-h（x1）|yj，x1∈V（T），j∈ [1，t2-1]}∪{h（yt2）-h（x2）}={1，2，…，q-1};

又，圖T有頂點n=p-1;

綜上所述，h（E（T））=[1，q-1]，h∈LTGS（T）。

（2）由于圖H有標號f∈LTGS（H），f（vs1）=p+q;

不失一般性，設f（vs1-1）=p+q-1，…，f（v1）=p+;

f（u1）=p，f（u2）=p+1，…，f（ut1）=q+;

因此有f（E（H））=f（E（H1））∪f（E（H2））∪{f（v1）-f（u1）};

其中f（E（H1））={f（vi）-f（u1）|u1，vi∈V（H），i∈[2，s1]}，f（E（H2））={f（uj）-f（v1）|uj，v1∈V（H），j∈[2，t1]};

即：f（E（H））={f（uv）|uv∈E（H）}=[1，q]

（3）設圖K∈F（G）有標號g∈∏（G）：

1）對于圖H，令g（vi）=f（vi）+p+q，g（uj）=f（uj）+p;

由（2）有g（vs1）=f（vs1）+p+q=2（p+q），g（vs1 -1）=

f（vs1-1）+p+q=f（vs1）-1+p+q=2（p+q）-1，…，g（v1）=f（v1）+p+q=p++p+q=p+q;g（u1）=f（u1）+p=2p， g（u2）=f（u2）+p=f（u1）+1+p=2p+1，…，g（ut1）=f（ut1）+p=f（u1）+s1-1+p=2p-1+s1;

因此g（v2）-g（u1）=p+q+1-2p=+q+1，g（v3） -g（u1）=p+q+2-2p=+q+2，…，g（vs1）-g（u1）=2（p+q）-2p=2q;g（v1）-g（u2）=p+q-2p-1=+q-1，…，g（v1）-g（ut1）=p+q-q-p=p;

又有g（v1）-g（u1）=p+q-2p=+q;g（E（H））={g（vi）-g（u1）|vi，u1∈V（H）}∪{g（v1）-g（uj）|v1，uj∈V（H）}∪{g（v1）-g（u1）};

其中{g（vi）-g（ui）|vi，u1∈V（H）}={1+q+，…，2q}，{g（v1）-g（uj）|v1，uj∈V（H）}={p，…，+q-1}，g（v1）-g（u1）=p+q-2p=p+q;

即：g（E（H））=[p，2p]。

2）對于圖T，令g（yj）=h（yj）+p+1，g（xi）=h（xi）+p+1;

不失一般性，可設g（yt2）=h（yt2）+p+1=g（x1）+ q-2;

由此推得：g（yt2-1）=h（yt2-1）+p+1=g（x1）+q-3，…，g（y1）=g（x1）+1;

令g（x1）=p+1，g（x2）=p;

因此有{g（yj）-g（x1）|x1，yj∈V（T）}={1，2，…，q-3};

注意到{g（yt2-1）-g（x2）}={q-2}，{g（yt2）-g（x2）}={q-1};

從而g（E（T））={g（yj）-g（x1）|x1，yj∈V（T）}∪{g（yt2-1）-g（x2）}∪{g（yt2）-g（x2）};

即：g（E（T））=[1，q-1];

（4）設M∈V（K），令g（M）=p+3;

由上述（3），總有點u∈V（T），g（u）=p+2;

使得：g（u）-g（M）=q;

因此有g（E（T））∪{q}={1，2，…，q-1}∪{q}=[1，q];

從而g（E（T））∪{q}∪g（E（H））={1，2，…，q-1}∪{q}∪{p，2q}=[1，2q];

綜上，有g（E（T））∪g（E（H））={1，2，…，q-1，q}∪{p，2q}=[1，2q];

即：g∈LTGS（G）;

又（E（K））={g（uv）|uv∈E（G）}=[1，2q];

由定義3，有g∈ΛEOTGL（G）。

定理2：

設圖K∈δEOTGGS（G），g∈ΛEOTGL（K），圖E有標號f∈∏（G）;若存點M∈V（T），U∈V（H），使得f（M）- f（U）=q，則f∈LTGS（G）。

證明：

由定理1，有：

（1）對于圖H，令f（vi）=g（vi）-1，f（uj）=g（uj）- 1;

有f（vs1）=g（vs1）-1=2（p+q）-1，f（vs1-1）=g（vs1-1）-1=g（vs1）-1-1=2（p+q）-2，…，f（v1）=g（v1）-1= p++p+q-1=p+q-1;f（u1）=g（u1）-1=2p-1，f（u2）=g（u2）-1=g（u1）+1-1=2p，…，f（ut1）=g（ut1）-1=g（u1）+t1-1-1=2q-2+t1;

因此有f（v2）-f（u1）=p+q-2p+1=+q+1，f（v3）- f（u1）=p+q+1-2p+1=+q+2，…，f（vs1）-f（u1）= 2（p+q）-1-2p+1=2q;f（v1）-f（u2）=p+q-1-2p= +q-1，…，f（v1）-f（ut1）=p+q-1-q-p+1=p;f（E（H））={f（vi）-f（u1）|vi，u1∈V（H）}∪{f（v1）- f（uj）|v1，uj∈V（H）}∪{f（v1）-f（u1）};

其中{f（vi）-f（u1）|vi，u1∈V（H）}={1+q+，…2q}，{f（v1）-f（uj）|v1，uj∈V（H）}={p，…，+q-1};

又f（v1）-f（u1）=p+q-1-2p+1=+q;

即：f（E（H））=[p，2q]。

（2）對于圖T，令f（yj）=g（yj）-1，f（xi）=g（xi）-1;

不失一般性，可設：f（yt2）=g（yt2）-1=g（x1）+q-3;

由此推得：f（yt2-1）=g（yt2-1）=g（x1）+q-4，…，f（y1）=g（x1）;

令f（x1）=p，f（x2）=p-1;

因此有{f（yj）-f（x1）|x1，yj∈V（T），j∈[1，t2-1]}={1，2，…，q-3};

注意到{f（yt2-1）-f（x2）}={q-2}，{f（yt2）-f（x2）}={q-1};

從而f（E（T））={f（yj）-f（x1）|x1，yj∈V（T），j∈[1，t2-1]}∪{f（yt2-1）-f（x2）}∪{f（yt2）-f（x2）};

即：f（E（T））=[1，q-1];

由上所述，存在點M∈V（T），且f（M）=p+2q;U∈V（H），f（U）=p+q，

使得f（M）-f（U）=q;

因此用一條邊將兩點U，M連接得到圖E，且f（E（E））=f（E（H））∪{f（U）-f（u1）}∪f（E（T））;

其中{f（U）-f（u1）}=g（x1）+1-2p+1}=p+2-2p+ 1}={q}，f（E（H））=[p，2q]，f（E（T））=[1，q-1];

即：f（E（E））=f（E（H））∪{f（U）-f（u1）}∪f（E（T））=[1，q-1]∪{q}∪[p，2q];

綜上所述，有f∈LTGS（G）。

3? 結? 論

由基本的圖模塊利用標號理論基于創新的可算法化的算法從中發現類似于網絡中節點的點是連結滿足一定條件下圖模塊的關鍵點，由可算法化過程看出此點能夠使得圖結構模塊化，基于一點變換而衍生的算法因密碼破譯困難使得安全性得到加強。由點連結演變成由邊連結使得圖模塊結構靈活多變，能組合各種所需圖結構，為快速大規模構造圖形結構和方便實際應用在理論上提供了保證。邊有序全優美標號與邊有序全優美空間的新定義、模塊化的組合與分解使得研究痕跡指向優美樹猜想，這有助于探索優美樹問題，希望下一步的研究在此方面有所收獲。

參考文獻：

[1] ROSA A. On certain valuations of the vertices of a graph [J]. Theory of Graphs，1967：349-355.

[2] GALLIAN J A. A Dynamic survey of graph labeling [J]. The Electronic Journal of Combinatorics，2012，18：1-7.

[3] EDWARDS M，HOWARD L. A survey of graceful trees [J]. Atlantic Electronic Journal of Mathematics，2006， 1（1）：5-30.

[4] BONDY J A，MURTY U.S.R. Graph theory with application [M]. New York：MaCmillan，1976.

[5] 姚明，趙振學，姚兵.關于樹（圖）的單點空間 [J].甘肅科學學報，2016，28（5）：15-18+78.

[6] 姚明，姚兵，謝建民.關于圖k-魔幻標號的若干結果 [J].甘肅科學學報，2010，22（1）：1-6.

[7] WILLIAM A，RAJAN B，RAJASINGH I，et al. Nor Super Edge Magic Total Labelling [C]//The Proceeding of the 4th International Workshop in Graph Labeling，Harbin Engineering University and University of Ballarat，Australia，2008：5-8.

[8] YAO B，ZHANG Z，YAO M，et al. A New Type of Magical Coloring [J].Advances in Mathematics，2008（5）：571-583.

[9] SUBBIAB S P. Super total graceful graphs and a tree conjeucture [J].Electronic Notes in Discrete Mathmatics，2015，48：301-304.

[10] GRAF A. A new graceful labeling for pendant graphs [J].Aequationes mathematicae，2014，87（1-2）：135-145.

作者簡介：姚明（1962-），男，漢族，江蘇揚州人，教授，本科，研究方向：圖著色和標號及計算優化。