基于模糊神經網絡的銑床熱誤差預測模型研究

李耀貴，伍先明

（廣東理工學院，廣東，肇慶 526100）

0 引言

數控機床是機械加工的重要設備。隨著智能化和信息化的不斷發展，機械加工正朝著高精度方向發展。我國長三角地區機械加工廠很多，在加工過程中，由于精度不達標，導致零部件尺寸不合格，甚至出現報廢現象。影響機床加工的誤差包括以下幾種：1）機床幾何誤差；2）機床熱誤差；3）切削力誤差；4）刀具磨損誤差；5）其它誤差。其中，熱誤差是影響數控機床加工精度的主要因素，限制了數控機床的發展[1]。為了提高機床加工精度，目前采用的方法主要包括以下兩種[2]：1）誤差防止法；2）誤差補償法。誤差防止法是通過優化機床結構，提高裝配精度，從而提高機床加工精度。但是，該方法需要成本太大，受到了限制。誤差補償法采用預測誤差來抵消機床產生的誤差，該方法成本較低，得到了迅速發展。因此，如何降低數控機床加工誤差，是學術界和工業急需解決的重大問題。

當前，學術界從不同角度對數控機床熱誤差展開了研究，產生了多種方法和理論。例如：文獻[3]研究了機床熱誤差徑向基函數神經網絡建模方法，討論了RBF神經網絡建模方法，給出了RBF神經網絡預測熱誤差模型，通過機床實際測量值驗證誤差模型的效果，結果顯示，可以采用RBF神經網絡預測數據對數控機床進行在線補償；文獻[4]研究了機床熱誤差不同神經網絡預測模型，通過比較 BP神經網絡、級聯神經網絡、徑向基函數神經網絡和廣義回歸神經網絡模型，以機床上熱誤差測量值進行比較和分析，四種網絡預測模型都有各自的優缺點，常規神經網絡模型熱誤差泛化能力較差。以往研究的機床熱誤差預測模型，預測精度較低，很難適應高精度機床加工的需求。本文結合模糊推理系統和RBF神經網絡結構的各自優點，建立模糊RBF神經網絡預測模型，通過銑床進行驗證，為進一步降低銑床加工產生的熱誤差提供參考。

1 徑向基函數(RBF)神經網絡

RBF神經網絡含有三層結構：1）輸入層；2）隱含層；3）輸出層。輸入層節點將輸入信號傳遞到隱含層，通過隱含層節點將信號輸出。隱含層節點采用高斯函數敘述，其表達式[5-7]為：

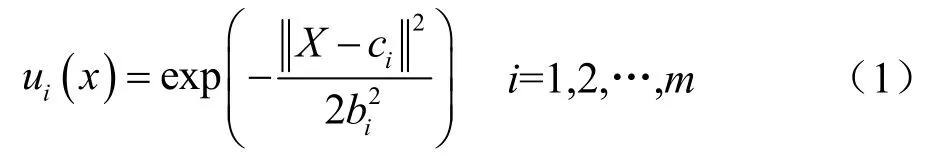
式中：ui(x)為隱含層第i個節點的輸出；X為輸入樣本，X=(x1,x2,···,xk)T；ci為隱含層第i個神經元中心矢量；bi為隱含層第i個神經元基函數寬度；m為隱含層節點個數。

在RBF神經網絡中，隱含層每個節點對應一個中心向量，該向量維數與輸入樣本相同，RBF神經網絡輸出層節點為線性組合。

2 熱誤差模糊RBF神經網絡

2.1 模糊理論

模糊推理系統結構如圖1所示，主要包括四個部分：1）模糊器；2）知識庫；3）推理運算；4）反模糊化。

圖1 模糊推理系統Fig.1 Fuzzy Inference System

模糊器將輸入值模糊化后，通過知識庫中模糊集模糊算子和模糊規則運算法則進行推理運算，最后采用反模糊器輸出值。模糊推理系統中的輸入和輸出值都是模糊集合，根據知識庫中的模糊規則進行計算。模糊規則一般采用條件語句，經過變化條件推理產生決策結果。模糊推理規則表達式[8-9]為：

2.2 模糊RBF神經網絡

結合模糊規則，可以推導出模糊 RBF神經網絡表達式為：

式中：xn為溫度輸入值；yo為神經網絡輸出值（模型預測值）。

模糊系統采用平均值法，其輸出值為：

式中：λi為第i條規則的激勵強度。

λi的表達式為：

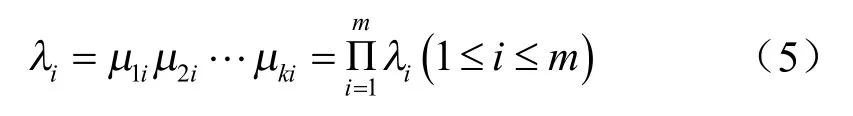
模糊RBF神經網絡預測模型結構如圖2所示。

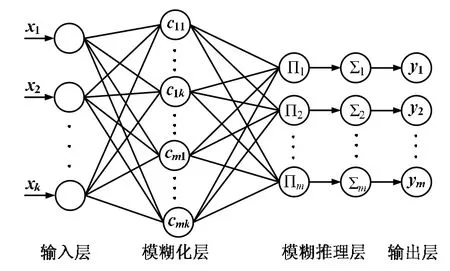
圖2 模糊神經網絡結構Fig.2 Structure of Fuzzy Neural Network

模糊RBF神經網絡結構包括四層：

第一層為輸入層：輸入值對應于神經網絡各個節點。

第二層為模糊化層：采用RBF為模糊隸屬度函數[10]，該層輸入輸出表達式為：

式中：yij為概率密度；θij為神經網絡模型訓練的均值。

第三層為模糊推理層：神經網絡節點與模糊規則相對應，每個節點輸出值表達式為：

式中：κi為模糊規則權函數；xij為第i個節點的輸入值。

第四層為輸出層：通過模糊推理層輸出信號的線性組合，采用平均法完成反模糊化計算，其輸出表達式為：

3 誤差與分析

采用溫度傳感器測量銑床主軸運行時溫度，傳感器分別采用激光位移傳感器和激光溫度傳感器，主軸轉速范圍為[1000 r/min，3000 r/min]。假設主軸轉速設置為1000 r/min、2000 r/min及3000 r/min，分別運行30 min，測量時間間隔為3 min，總共測量 30組溫度值。將測量數據導入到預測模型中，具體實驗方案如圖3所示。

圖3 實驗方案Fig.3 Experimental scheme

銑床熱誤差測量實驗過程如圖4所示，激光位移傳感器和激光溫度位移傳感器分布位置如圖5所示，采用溫度傳感器測量的溫度結果如圖6所示，采用激光位移傳感器測量結果如表1所。

圖4 銑床熱誤差測量實驗過程Fig.4 Experimental Process of milling machine thermal error measurement

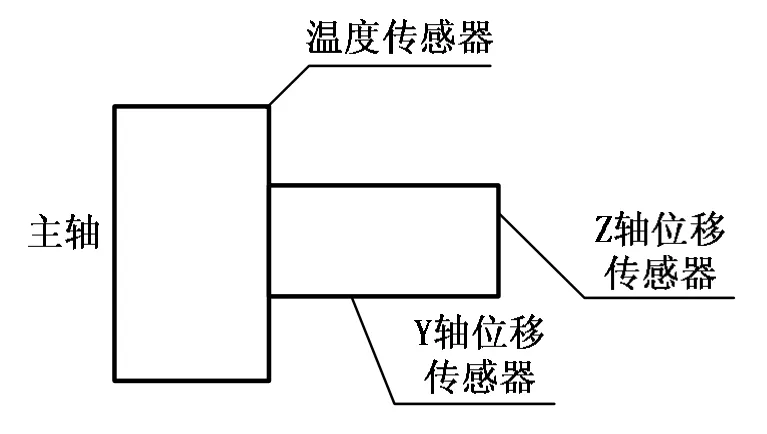
圖5 傳感器分布位置Fig.5 Sensor distribution position

圖6 測量溫度數據Fig.6 Measuring temperature data

表1 主軸測量與模型預測值Table.1 Spindle measurement and model prediction value

Y軸方向預測值與實際測量值誤差如圖 7所示，Z軸方向預測值與實際測量值誤差如圖8所示。根據圖7預測結果可知：銑床主軸在Y方向上產生的熱誤差，采用RBF神經網絡模型預測誤差較大，預測誤差最大值為5.9 μm，模糊RBF神經網絡模型預測誤差較小，預測誤差最大值為3.5 μm。根據圖8預測結果可知：銑床主軸在Z方向上產生的熱誤差，采用RBF神經網絡模型預測誤差較大，預測誤差最大值為7.1 μm，模糊RBF神經網絡模型預測誤差較小，預測誤差最大值為2.9 μm。因此，采用 RBF神經網絡模型預測主軸熱誤差，其精度較低，而采用模糊 RBF神經網絡模型預測主軸熱誤差，其精度較高。

圖7 銑床Y軸方向誤差Fig.7 Y-axis direction error of milling machine

圖8 銑床Z軸方向誤差Fig.8 Z-axis direction error of milling machine

4 結語

本文在模糊推理系統基礎上，創建模糊 RBF神經網絡結構，并用于預測銑床主軸產生的熱誤差，主要結論如下：

1）銑床主軸運行過程中，容易產生熱誤差，銑床主軸不同方向產生的熱誤差也不一樣，必須對誤差進行補償，才能提高銑床加工精度。

2）傳統RBF神經網絡預測模型預測精度較低，誤差范圍在8 μm以內。模糊RBF神經網絡預測模型預測精度加高，誤差范圍在4 μm以內。

3）主軸運行過程中，熱誤差隨著溫度的變化而變化，主軸熱誤差與伺服軸上精度關系可以作為未來深入研究的方向。