高三解析幾何解題教學(xué)中的幾點(diǎn)做法

(郵編：230601)

安徽省合肥市第三十二中學(xué)

1 問(wèn)題背景

在2018年高三二模考試前的月考和平時(shí)試卷批改中，筆者多次發(fā)現(xiàn)數(shù)學(xué)解答題得分較少的是第20道題——解析幾何.

(1)求橢圓C的標(biāo)準(zhǔn)方程；

(2)若不經(jīng)過(guò)橢圓C的右焦點(diǎn)F的直線(xiàn)l:y=kx+m(k<0,m>0)與橢圓C交于A、B兩點(diǎn)，且與圓x2+y2=1相切.試探究△ABF的周長(zhǎng)是否為定值，若是，求出定值；若不是，請(qǐng)說(shuō)明理由.

從答卷上來(lái)看，有的同學(xué)只做了兩問(wèn)中的第一小問(wèn)；有的對(duì)第二小問(wèn)也只是寫(xiě)了一點(diǎn)點(diǎn)，如聯(lián)立一個(gè)方程組，搭了個(gè)簡(jiǎn)單的框架就不了了之，能做完的同學(xué)為數(shù)極少.

2 原因探究

解析幾何作為高中數(shù)學(xué)的重要板塊，承擔(dān)著培育學(xué)生數(shù)學(xué)的兩大核心素養(yǎng)，即邏輯思維和計(jì)算能力的重任，作為數(shù)學(xué)老師在學(xué)科教育上應(yīng)抓住高三全面復(fù)習(xí)的契機(jī)著力落實(shí)，這不僅僅是為了高考的得分，更重要的是為學(xué)生的后續(xù)學(xué)習(xí).為此，高三年級(jí)組對(duì)不同層次的學(xué)生就這種現(xiàn)象進(jìn)行了座談.根據(jù)座談的結(jié)果，我們將學(xué)生分成以下三類(lèi)：第一類(lèi)學(xué)生只會(huì)做第一問(wèn)，對(duì)第二問(wèn)由于缺少邏輯推理能力而不知如何下筆，建構(gòu)不了知識(shí)框架；第二類(lèi)學(xué)生明確解題方向，能搭建解題框架，但因?yàn)橛?jì)算方法選擇不當(dāng)，計(jì)算過(guò)程過(guò)于繁瑣，導(dǎo)致無(wú)法將計(jì)算堅(jiān)持到底；第三類(lèi)學(xué)生有較好的計(jì)算能力，但由于缺少必要的訓(xùn)練，在解題中缺少必勝的信念，從而框架搭好了就此擱淺.

針對(duì)學(xué)生解題中出現(xiàn)的這些問(wèn)題，教師如何教學(xué)才能改變解析幾何解答中出現(xiàn)的荒蕪局面呢？

3 改進(jìn)措施

現(xiàn)將年級(jí)組老師們的建議總結(jié)提煉后，提出要從信念、框架、計(jì)算這三個(gè)方面著手來(lái)改進(jìn)解析幾何復(fù)習(xí)教學(xué)，改變以前為趕復(fù)習(xí)進(jìn)度而忽視學(xué)情的講授式模式.為此，在后期的復(fù)習(xí)中，我們采用了以下流程來(lái)幫助學(xué)生攻克解析幾何：首先通過(guò)簡(jiǎn)單題來(lái)夯實(shí)雙基，幫助學(xué)生堅(jiān)定信念增強(qiáng)信心；再用分層框架來(lái)破解典例；掌握常用技能簡(jiǎn)化和優(yōu)化計(jì)算；最后進(jìn)行對(duì)點(diǎn)強(qiáng)化訓(xùn)練.下面用實(shí)例來(lái)闡述具體的做法，以與同仁共享.

3.1 堅(jiān)定信念 增強(qiáng)嘗試信心

解析幾何因計(jì)算難而讓不少師生制定了這樣的備考策略：第一問(wèn)必做，對(duì)第二問(wèn)如果難就選擇放棄.在這樣的指導(dǎo)思想下，即使看似難題，但稍加努力就能解決的問(wèn)題也會(huì)因此而空缺.

波利亞曾說(shuō)：“認(rèn)為解題純粹是一種智力活動(dòng)是錯(cuò)誤的，決心和情緒所起的作用很重要，教學(xué)生解題是意志的教育”.同時(shí)越來(lái)越多的研究表明：動(dòng)機(jī)和信念在問(wèn)題解決過(guò)程中同樣有重要的意義.筆者贊同以上觀點(diǎn)，認(rèn)為解析幾何復(fù)習(xí)中幫助學(xué)生樹(shù)立戰(zhàn)勝困難的信心比框架、計(jì)算顯得更為重要.如對(duì)于問(wèn)題背景中的第(2)問(wèn)，教師可以在學(xué)生已做出(1)問(wèn)的基礎(chǔ)上，鼓勵(lì)學(xué)生用數(shù)學(xué)語(yǔ)言去翻譯：①直線(xiàn)l與C相交和②直線(xiàn)l與圓x2+y2=1相切這兩個(gè)條件.至于這兩步得出的結(jié)論怎么用，教師可以先不說(shuō).再引導(dǎo)學(xué)生嘗試去寫(xiě)△ABF周長(zhǎng)的表達(dá)式.這時(shí)學(xué)生會(huì)遇到如何表示|AB|、|AF|和|BF|的困難.教師適時(shí)點(diǎn)撥，進(jìn)一步引導(dǎo)他們?cè)鯓永们皟刹剑@樣逐步引導(dǎo)他們嘗試去解決.讓他們?cè)趯?shí)踐中積累解題經(jīng)驗(yàn)，在問(wèn)題解決中體驗(yàn)成功的快樂(lè)，在戰(zhàn)勝困難中堅(jiān)定信念.

愛(ài)因斯坦說(shuō)得好，他認(rèn)為信念最好能由經(jīng)驗(yàn)和明確的思想來(lái)支持.這說(shuō)明除了有意識(shí)，還要有活動(dòng)經(jīng)驗(yàn)，而經(jīng)驗(yàn)的獲得來(lái)自于大量的實(shí)踐.信念的培養(yǎng)不是老師幾句鼓勵(lì)的話(huà)就能樹(shù)立的，它需要有扎實(shí)的基礎(chǔ)，教師的有效示范，學(xué)生的積極內(nèi)化和有素的訓(xùn)練來(lái)支撐.

3.2 搭建框架 明確解題方向

(Ⅰ)求C的方程；

(Ⅱ)設(shè)直線(xiàn)l不經(jīng)過(guò)P2點(diǎn)且與C相交于A、B兩點(diǎn).若直線(xiàn)P2A與直線(xiàn)P2B的斜率的和為-1，證明：l過(guò)定點(diǎn).

做法剖析：

(1)根據(jù)邏輯關(guān)系，搭建分層框架，對(duì)本題的第二問(wèn)采用分析法執(zhí)果索因.

尋結(jié)論成立的條件，步步為營(yíng)理清解題思路，消除解題的盲目性，增加解題的信心.通過(guò)化整為零，將解題過(guò)程分成若干層.根據(jù)層與層之間的邏輯關(guān)系建立起框架，然后自下而上進(jìn)行書(shū)寫(xiě).具體如下：

(2)理清條件關(guān)系，翻譯每層內(nèi)容

為了表達(dá)的需要，引導(dǎo)學(xué)生大膽設(shè)出未知量，將題中的條件關(guān)系用數(shù)學(xué)符號(hào)或式子來(lái)表達(dá)，在框架的指引下理清k和m的邏輯關(guān)系，朝目標(biāo)方向努力.

第一層：特殊情況驗(yàn)證.

一般情況證明：

聯(lián)立方程，得出兩點(diǎn)間坐標(biāo)的關(guān)系，用兩點(diǎn)的坐標(biāo)表示斜率和.

設(shè)l：y=kx+m(m≠1)，A(x1，y1)，B(x2，y2).

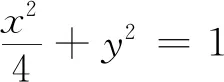
第二層：利用韋達(dá)定理，根據(jù)斜率和為-1，尋找k與m的關(guān)系式.

第三層：消去k，將其方程化為點(diǎn)斜式，從而得出定點(diǎn).

(3)對(duì)點(diǎn)練習(xí)，訓(xùn)練思維 選擇相應(yīng)的模擬題，讓學(xué)生分析，進(jìn)行解題前邏輯思維訓(xùn)練.采用獨(dú)立思考，暢談解法,優(yōu)化解法這樣的課堂活動(dòng)來(lái)激發(fā)學(xué)生的解題熱情，開(kāi)發(fā)學(xué)生解題潛能.

3.3 簡(jiǎn)化計(jì)算 助推正解得出

解析幾何的特點(diǎn)是計(jì)算難，如果計(jì)算方向不明確，方法繁雜會(huì)導(dǎo)致整個(gè)解題全盤(pán)崩潰.因而當(dāng)學(xué)生面對(duì)問(wèn)題時(shí)，首先要引導(dǎo)學(xué)生多想少算，明確計(jì)算對(duì)象，優(yōu)選解題方法，設(shè)計(jì)合理的運(yùn)算途徑.框架構(gòu)建好后，要求學(xué)生再想一想，尋找恰當(dāng)?shù)挠?jì)算方法，以便簡(jiǎn)化運(yùn)算過(guò)程而獲得優(yōu)解.常用的簡(jiǎn)化計(jì)算方法有：追根溯源，回歸定義；平面幾何滲透，數(shù)形結(jié)合；設(shè)而不求，整體運(yùn)算；利用韋達(dá)定理化繁為簡(jiǎn)等.

圖1

(Ⅰ)當(dāng)t=4，|AM|=|AN|時(shí)，求△AMN的面積；

(Ⅱ)當(dāng)2|AM|=|AN|時(shí)，求k的取值范圍.

做法剖析 (Ⅰ)解略；(Ⅱ)條件中|AM|和|AN|都是弦長(zhǎng)，因而需要利用弦長(zhǎng)公式，于是聯(lián)立方程求出|AM|.為簡(jiǎn)化計(jì)算，再利用MA⊥NA，在|AM|已得出的基礎(chǔ)上，直接求出|AN|.

(1)設(shè)而不求，整體代入

(2)利用垂直，避免重復(fù)

(3)挖掘隱含條件，建立不等關(guān)系

(4)對(duì)點(diǎn)練習(xí)，強(qiáng)化計(jì)算

讓學(xué)生在練習(xí)中逐步掌握運(yùn)算技能，在計(jì)算中磨練意志，消除對(duì)解幾的畏懼心理.

(1)求橢圓C的標(biāo)準(zhǔn)方程；

4 改進(jìn)后的反思

在框架分層式的解題解學(xué)中，框架有助于學(xué)生按照邏輯關(guān)系尋找解題方向，

分層有助于梳理?xiàng)l件，分解難點(diǎn).而一些簡(jiǎn)化計(jì)算方法的掌握便于學(xué)生優(yōu)化計(jì)算，使計(jì)算變得更流暢.對(duì)點(diǎn)訓(xùn)練讓學(xué)生從解題的模仿開(kāi)始，逐步訓(xùn)練思維和提高計(jì)算能力.通過(guò)一段時(shí)間的訓(xùn)練，取得了一定的成效.從學(xué)生的答卷來(lái)看，回答解幾大題第二問(wèn)的同學(xué)越來(lái)越多，能堅(jiān)持做完的同學(xué)也多了起來(lái)，該題年級(jí)平均得分在逐步提高.在嘗試的過(guò)程中，感觸較多，反思感悟可總結(jié)成以下三點(diǎn)：

反思一不憤不啟，學(xué)會(huì)忍

不憤不啟是指不到學(xué)生們想弄明白而還沒(méi)有弄明白時(shí)，不去啟發(fā)他.在課堂上我們經(jīng)常看到學(xué)生解這類(lèi)題會(huì)跑偏，出現(xiàn)一開(kāi)始解題方向不對(duì)，選擇的計(jì)算方法過(guò)于繁瑣，跌跌撞撞艱難向前的現(xiàn)象.這時(shí)的老師要學(xué)會(huì)忍，不要馬上就呈現(xiàn)解答.要讓學(xué)生在挫折中探索解題方向，以便能更好地磨練他們計(jì)算耐力，讓他們更深刻地去體會(huì)計(jì)算背后的算理.啟發(fā)時(shí)先多問(wèn)問(wèn)學(xué)生是如何想的，為什么這樣想，然后貼近學(xué)生的認(rèn)知去啟發(fā).切不可急于兜售自己的想法，而掐滅學(xué)生思維的火花.

反思二不舍不得，學(xué)會(huì)放

對(duì)解析幾何的復(fù)習(xí)，教師要敢舍，認(rèn)為多講一些題型，學(xué)生就能搞好是老師們的一廂情愿.對(duì)學(xué)生解題思路和計(jì)算能力的訓(xùn)練，雖然開(kāi)始訓(xùn)練時(shí)很費(fèi)時(shí)間，但教師也要舍得把寶貴的課堂時(shí)間放手給學(xué)生去嘗試，即便一堂課只解決一道題,只要學(xué)生能真正理解掌握也是值得的.授之以魚(yú)不如授之以漁，沒(méi)舍就沒(méi)有得！

反思三不急不躁，學(xué)會(huì)聽(tīng)

一道解析幾何題，它的的解法往往有多種.教師的解法不是權(quán)威，我們要放下權(quán)威，更多地去關(guān)注學(xué)生的想法.借學(xué)生的口讓各種解法“百花齊放”起來(lái)，讓他們?cè)谒季S碰撞中尋找最優(yōu)解.即使學(xué)生的解法很拙劣，教師也要不急不躁，耐心去傾聽(tīng)，呵護(hù)學(xué)生參與思考的積極性.

總之，對(duì)解析幾何的復(fù)習(xí)，我們既要從意識(shí)層面去落實(shí)，調(diào)動(dòng)學(xué)生的一切非智力因素的參與；又要從實(shí)踐層面上加以夯實(shí).用信念、框架和計(jì)算這樣的三套車(chē)齊驅(qū)并駕我們高三解析幾何的復(fù)習(xí)，相信一定不會(huì)辜負(fù)“把立德樹(shù)人作為教育的根本任務(wù)”的歷史使命！