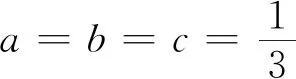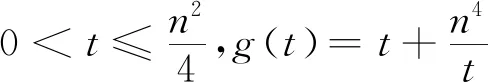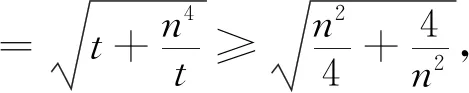活躍在不等式試題中的閔可夫斯基不等式

(郵編：430074)

武漢職業技術學院商學院

本文選取各類試題中的不等式問題，巧妙地運用閔可夫斯基不等式來秒殺，筆者給出如下幾例應用說明，希望給大家帶來幫助.

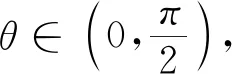
解由閔可夫斯基不等式可得

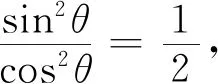
解由閔可夫斯基不等式可得

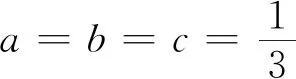
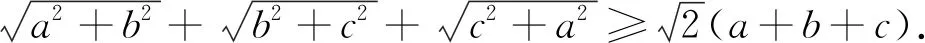
此題在文[1]的證法從取等號條件入手確定λ值，巧用柯西不等式求證，運用閔可夫斯基不等式可以秒殺文[1]中的問題.

證明由閔可夫斯基不等式可得

解由閔可夫斯基不等式可得

由上述問題聯想2018年重慶數學夏令營試題第一試壓軸題如下

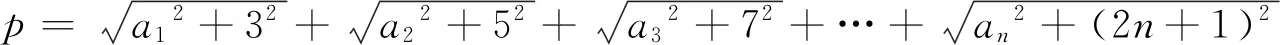
即20182+(n2+2n)2=m2，則[m-(n2+2n)][m+(n2+2n)]=20182=(2×1009)2.

由n2+2n-m與n2+2n+m奇偶性相同，且1009為質數，可得

例4 (安振平先生博客問題4922)設a、b∈R+，且ab=a+b.

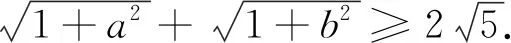
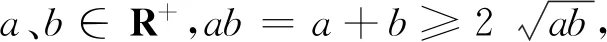
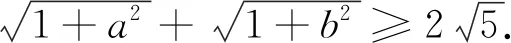
類似問題(安振平先生博客問題4921)設a、b、c∈R+且ab+bc+ca=a+b+c.

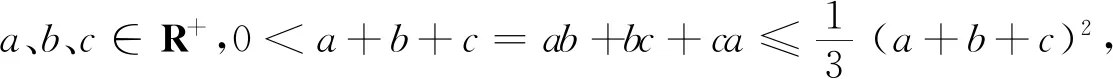
由閔可夫斯基不等式可得