導體材料渦流熱成像應(yīng)力檢測的仿真

(四川大學 制造科學與工程學院，成都 610065)

工業(yè)零部件在生產(chǎn)、加工及使用過程中，會受到外部載荷的作用，從而在材料的局部區(qū)域產(chǎn)生應(yīng)力集中，致使材料的力學性能降低，甚至導致材料失效。因此，對材料或結(jié)構(gòu)的應(yīng)力狀態(tài)進行檢測與監(jiān)測，特別是采用無損檢測方法進行檢測與監(jiān)測是很有必要的。在眾多的無損檢測方法中，渦流熱成像檢測(ECT)技術(shù)可以快速地檢測試件表面或近表面的缺陷，如表面裂紋[1-3]、腐蝕缺陷[4-6]、焊接缺陷[7-9]、疲勞損傷[10-12]等。同超聲法、射線法等相比，ECT方法具有非接觸、單次檢測面積大、對復雜形狀零件的易適應(yīng)性等優(yōu)點，可用于大范圍內(nèi)的應(yīng)力先驗檢測。近幾年，不少專家學者將渦流熱成像檢測技術(shù)應(yīng)用于金屬材料沖擊損傷應(yīng)力、拉伸應(yīng)力的檢測中，并取得了一定的研究成果。通過檢測多次沖擊后的鋼板，劉錄葉等證明了應(yīng)用ECT檢測沖擊殘余應(yīng)力是可行的[13]；利用ECT檢測拉伸應(yīng)力，有學者給出了材料縱向和橫向電磁特性的變化規(guī)律[14]以及應(yīng)力和熱導率之間的線性耦合關(guān)系[15]；雷慶等有效定量了單向拉伸載荷下鋼結(jié)構(gòu)的表面應(yīng)力[16]等。但在實際應(yīng)力檢測中，預(yù)制一定量大小及分布厚度的應(yīng)力樣本試件比較困難，結(jié)果量化也比較復雜。因此，筆者采用數(shù)值仿真分析手段，通過設(shè)置材料局部區(qū)域的電導率、熱導率等參數(shù)的大小及其厚度來模擬實際應(yīng)力層，建立渦流熱成像仿真模型并分析試件表面溫度響應(yīng)的變化情況，試圖為渦流熱成像定量檢測材料或結(jié)構(gòu)的應(yīng)力提供理論參考。

1 ECT應(yīng)力檢測原理

應(yīng)用ECT技術(shù)檢測導體材料的應(yīng)力分布時，含應(yīng)力區(qū)域的感應(yīng)渦流密度大小是異于正常區(qū)域的，且與應(yīng)力幅值相關(guān)，應(yīng)力幅值的改變會導致材料電磁特性參數(shù)和傳熱特性參數(shù)的改變，從而使得感應(yīng)焦耳熱在材料內(nèi)部傳導的速度發(fā)生改變，最終表現(xiàn)為熱成像圖像溫度場的不均勻分布和應(yīng)力區(qū)與非應(yīng)力區(qū)的溫升變化規(guī)律的不一致。通過對ECT熱成像圖像/序列的后期處理分析，可以獲得材料的應(yīng)力狀態(tài)，其檢測理論模型如圖1所示。電導率變化主要影響檢測過程中的感應(yīng)加熱，熱導率主要影響冷卻過程中的熱傳導。

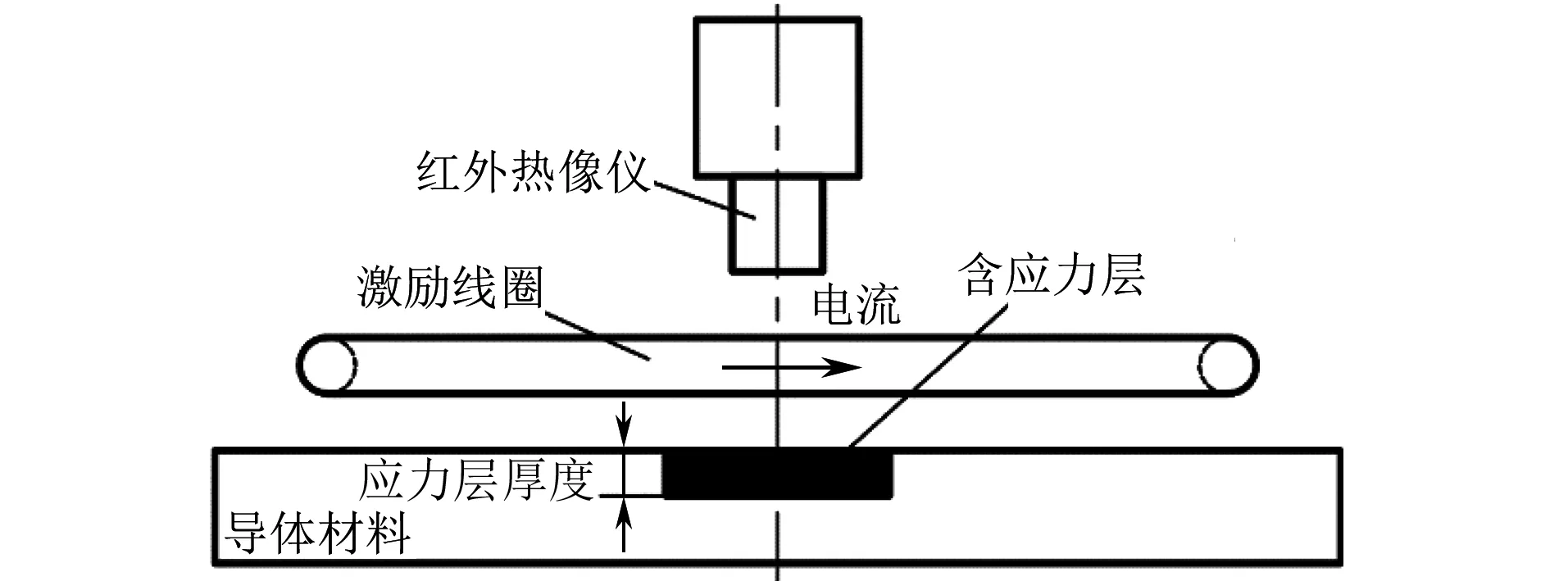
圖1 ECT應(yīng)力檢測理論模型

1.1 檢測原理

渦流熱成像技術(shù)在檢測過程中所涉及到的物理過程有：感應(yīng)渦流加熱、熱傳導、紅外輻射[17]。當激勵線圈中通有一定頻率的交變電流時，會產(chǎn)生電磁感應(yīng)現(xiàn)象，即在被測導體內(nèi)會感應(yīng)出相同頻率的電渦流，由麥克斯韋爾方程推導出該渦流場的控制方程如式(1)所示。

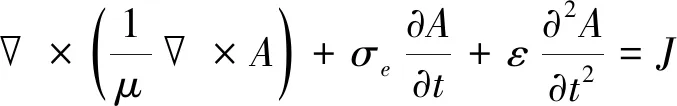
(1)

式中：μ為材料的磁導率；A為磁矢勢；σe為材料的電導率；ε為介電常數(shù)；J為外部電流密度;t為電磁激勵作用時間。

產(chǎn)生的渦流會產(chǎn)生集膚效應(yīng)，積聚在被測導體表面，其集膚深度dJ的計算公式如式(2)所示。

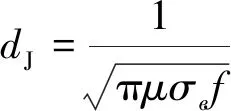
(2)

式中：f為激勵電流頻率。

由焦耳定律可知，部分渦流會在導體內(nèi)部由電能轉(zhuǎn)換為熱能，產(chǎn)生的焦耳熱Q正比于渦流密度Js和電場強度E，其計算公式如式(3)所示。

(3)

由式(3)可知，影響焦耳熱的因素主要有導體材料的電導率和渦流密度，但因為電導率也會影響渦流的密度值，因此焦耳熱與電導率不是單純的負冪次關(guān)系，其變化規(guī)律還需要進一步探討。

在感應(yīng)加熱階段產(chǎn)生的焦耳熱Q會在被測試件內(nèi)部進行傳遞，其傳遞規(guī)律及熱擴散深度dT的計算公式如式(4)，(5)所示。

(4)

(5)

式中：ρ為材料密度；Cp為材料的比熱容；T為材料熱力學溫度；λ為材料的熱導率；α=λ/(ρCp)為導體熱擴散系數(shù);t為熱擴散的時間。

1.2 應(yīng)力對導體材料屬性的影響

1.2.1 金屬電阻應(yīng)變效應(yīng)

導體材料內(nèi)部應(yīng)力會使得材料內(nèi)部原子間的距離和點陣的動畸變發(fā)生變化，導致材料的電阻率發(fā)生變化，從而影響材料的電導率[15，18]。一般情況下，電導率隨應(yīng)力的變化呈負指數(shù)關(guān)系，當指數(shù)的絕對值遠遠小于1時，則略去高階小項，近似成為線性關(guān)系。其影響規(guī)律遵循式(6)[19]。

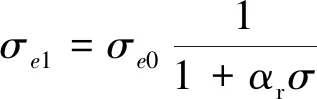
(6)

式中：σe1為導體存在應(yīng)力時的電導率；σe0為導體無應(yīng)力時的電導率；σ為應(yīng)力值(拉應(yīng)力為正、壓應(yīng)力為負)；αr為應(yīng)力系數(shù)。

即當試件存在拉應(yīng)力時，其應(yīng)力區(qū)域的電導率將減小相反，當試件存在壓應(yīng)力時，其應(yīng)力區(qū)域的電導率將增大。

在檢測過程中，由于被測試件產(chǎn)生的焦耳熱會影響材料本身的溫度，且電導率會隨溫度的變化而發(fā)生變化，其關(guān)系遵循式(7)。

(7)

式中：σeT，σeT0分別為材料在溫度T，T0時的電導率；β為導體電阻溫度系數(shù)。

1.2.2 魏德曼-弗蘭茲定律

由魏德曼-弗蘭茲定律可知，在室溫下很多金屬的熱導率與電導率之比幾乎相同，如式(8)所示。因此當被測試件內(nèi)部存在應(yīng)力時，應(yīng)力區(qū)域的熱導率也會隨著電導率的改變而發(fā)生相應(yīng)改變。

(8)

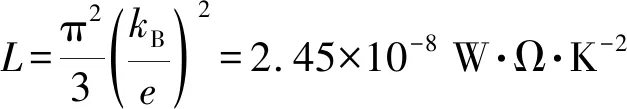
設(shè)λ0為無應(yīng)力時的熱導率，λ1為存在應(yīng)力時的熱導率。設(shè)置仿真模型參數(shù)時，同電導率一樣，當試件存在拉應(yīng)力時，將試件應(yīng)力區(qū)域的熱導率λ1同σe1等比例減小；相反，當試件存在壓應(yīng)力時，將λ1同σe1等比例增大。

圖2 渦流熱成像檢測的仿真模型及其網(wǎng)格劃分

2 ECT應(yīng)力檢測仿真模型

渦流熱成像檢測過程中，被測試件溫升的熱源主要來自導體材料的電磁損耗，在進行數(shù)值仿真分析時，需要耦合電磁場和溫度場。文章用COMSOL MUTIPHYSICS多物理仿真軟件建立了脈沖渦流熱成像檢測的三維模型，模型及其網(wǎng)格劃分如圖2所示。選取電磁場與熱傳導兩個物理場進行耦合，并將熱傳導模式設(shè)置為固體傳熱，通過瞬態(tài)分析獲取激勵加熱階段和自然冷卻階段的溫度場變化情況。激勵線圈直徑為6 mm，長150 mm，距檢測表面的提離為1 mm；導體材料的尺寸(長×寬×厚)為200 mm×120 mm×10 mm，中部存在(長×寬)20 mm×20 mm的區(qū)域為電導率及熱導率變化層，厚度可變，模擬被測試件存在應(yīng)力的區(qū)域；初始溫度設(shè)置為293 K，激勵電流設(shè)置為500 A，加載頻率為250 kHz，加熱時間為500 ms，冷卻時間為1 000 ms，即總的檢測時間為1 500 ms。

仿真所用導體材料的參數(shù)見表1，由式(5)計算出材料正常區(qū)域在檢測結(jié)束后的熱擴散深度可達到4.231 mm，即在研究應(yīng)力層厚度對溫度響應(yīng)曲線的影響時，最大厚度不能超過4.231 mm。

表1 仿真所用材料的參數(shù)

3 COMSOL仿真結(jié)果討論

在分析仿真結(jié)果的過程中，分別考查被測導體表面點1(位于試件應(yīng)力層中部)和點2(位于遠離應(yīng)力層的正常區(qū)域處)的溫度響應(yīng)變化情況。如圖3所示，點1,點2的檢測值分別代表應(yīng)力層及遠離應(yīng)力層的正常區(qū)域的表面溫度值，以下曲線原始數(shù)據(jù)點均是基于點1,點2處的溫度值所繪制。

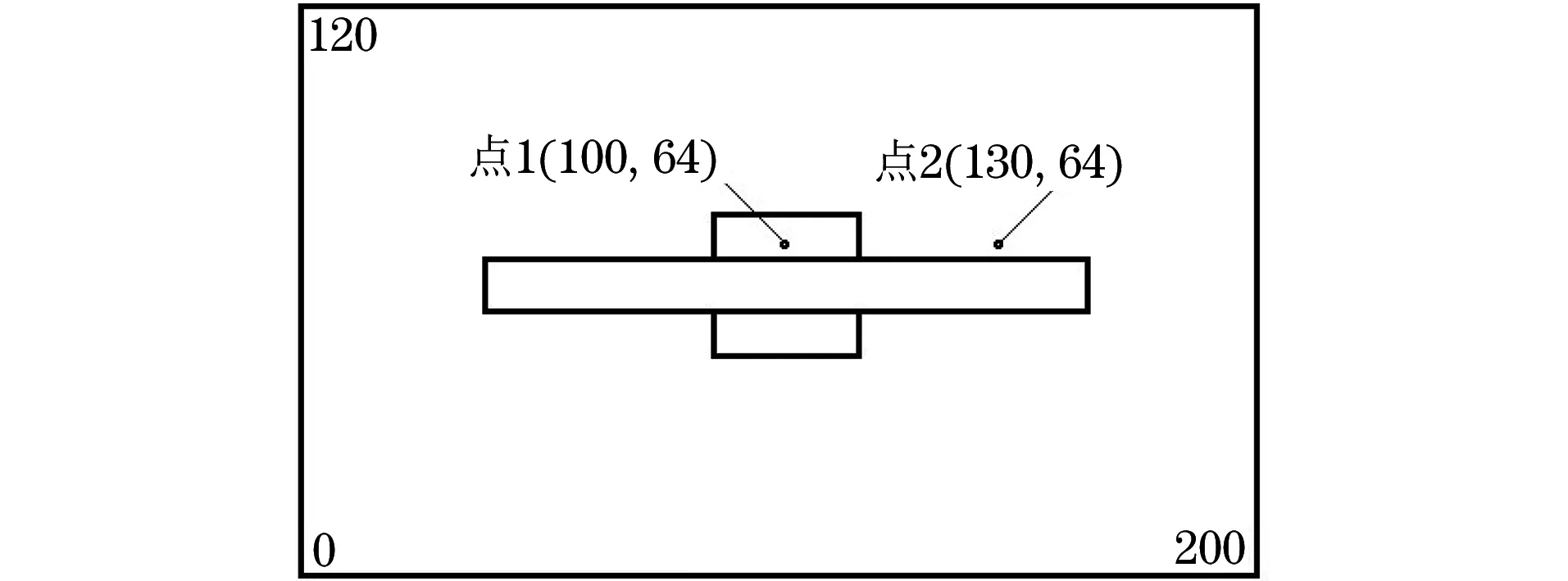
圖3 數(shù)據(jù)取點位置示意

3.1 電導率、熱導率變化與檢測結(jié)果的關(guān)系

電導率、熱導率變化層即所模擬的應(yīng)力層，其厚度設(shè)置為1 mm，導體正常區(qū)域的電導率σe0設(shè)置為5.0×106S·m-1，為得到較光滑的仿真曲線，應(yīng)力區(qū)域的電導率σe1設(shè)置如下：從1.0×105S·m-1以1.0×105S·m-1的增量逐次增加至5.0×106S·m-1，模擬拉應(yīng)力層；再繼續(xù)從5.0×106S·m-1以1.0×105S·m-1的增量逐次增加至1.0×107S·m-1，模擬壓應(yīng)力層。其中，熱導率與電導率呈等比例變化，因此后續(xù)結(jié)果分析中只列出了電導率與溫度值的關(guān)系。結(jié)合仿真結(jié)果，探討上述變化過程中被測試件表面溫升曲線的響應(yīng)情況。改變層電導率對導體表面溫度分布的影響如圖4所示。

圖4 改變層電導率對導體表面溫度分布的影響

圖5 不同電導率對應(yīng)點1,點2處的溫度響應(yīng)曲線

由圖4可見，被測導體拉應(yīng)力層區(qū)域的溫度明顯高于標準件的，且拉應(yīng)力越大，應(yīng)力層感應(yīng)渦流越集中，加熱結(jié)束及冷卻結(jié)束時的高溫區(qū)越明顯；相反，壓應(yīng)力層區(qū)域的溫度低于標準件的，壓應(yīng)力越大，應(yīng)力層感應(yīng)渦流越分散，低溫區(qū)范圍越大。不同電導率對應(yīng)點1，點2處的溫度響應(yīng)曲線如圖5所示，可以看出電導率的改變對點1處的溫度影響較大，基于此可評估應(yīng)力大小的變化情況，而遠離應(yīng)力區(qū)域的點2處溫度幾乎不受電導率變化影響，可以其作為拉、壓應(yīng)力層溫度的參照值。

圖6 加熱結(jié)束時電導率變化對點1、點2處溫度值的影響

圖6是應(yīng)力區(qū)域點1處與正常區(qū)域點2處在加熱結(jié)束時的溫度T1,T2隨電導率、熱導率變化的曲線圖，從圖中可以看出，拉應(yīng)力層電導率越小，應(yīng)力區(qū)溫度高于正常區(qū)且溫差越大；壓應(yīng)力層電導率越大，應(yīng)力區(qū)溫度低于正常區(qū)且溫差也越大。通過式(6)反演導體電導率與其應(yīng)力絕對值(不考慮拉、壓應(yīng)力的正負問題)之間的關(guān)系，如式(9)所示，并繪制應(yīng)力大小變化與點1、點2處溫度差值(T1-T2)之間的關(guān)系曲線圖，如圖7所示。

(9)

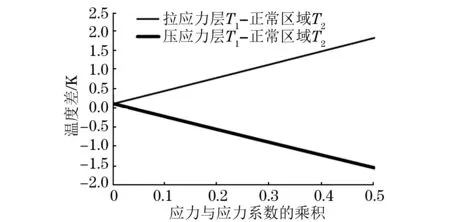
圖7 應(yīng)力變化對溫度的影響

結(jié)果表明，在一定范圍內(nèi)，導體應(yīng)力值與表面應(yīng)力區(qū)域和正常區(qū)域的溫度差近似為線性關(guān)系。拉應(yīng)力越大，應(yīng)力區(qū)與正常區(qū)的正溫差越大；壓應(yīng)力越大，應(yīng)力區(qū)與正常區(qū)的負溫差越大。

3.2 應(yīng)力層厚度變化與檢測結(jié)果的關(guān)系

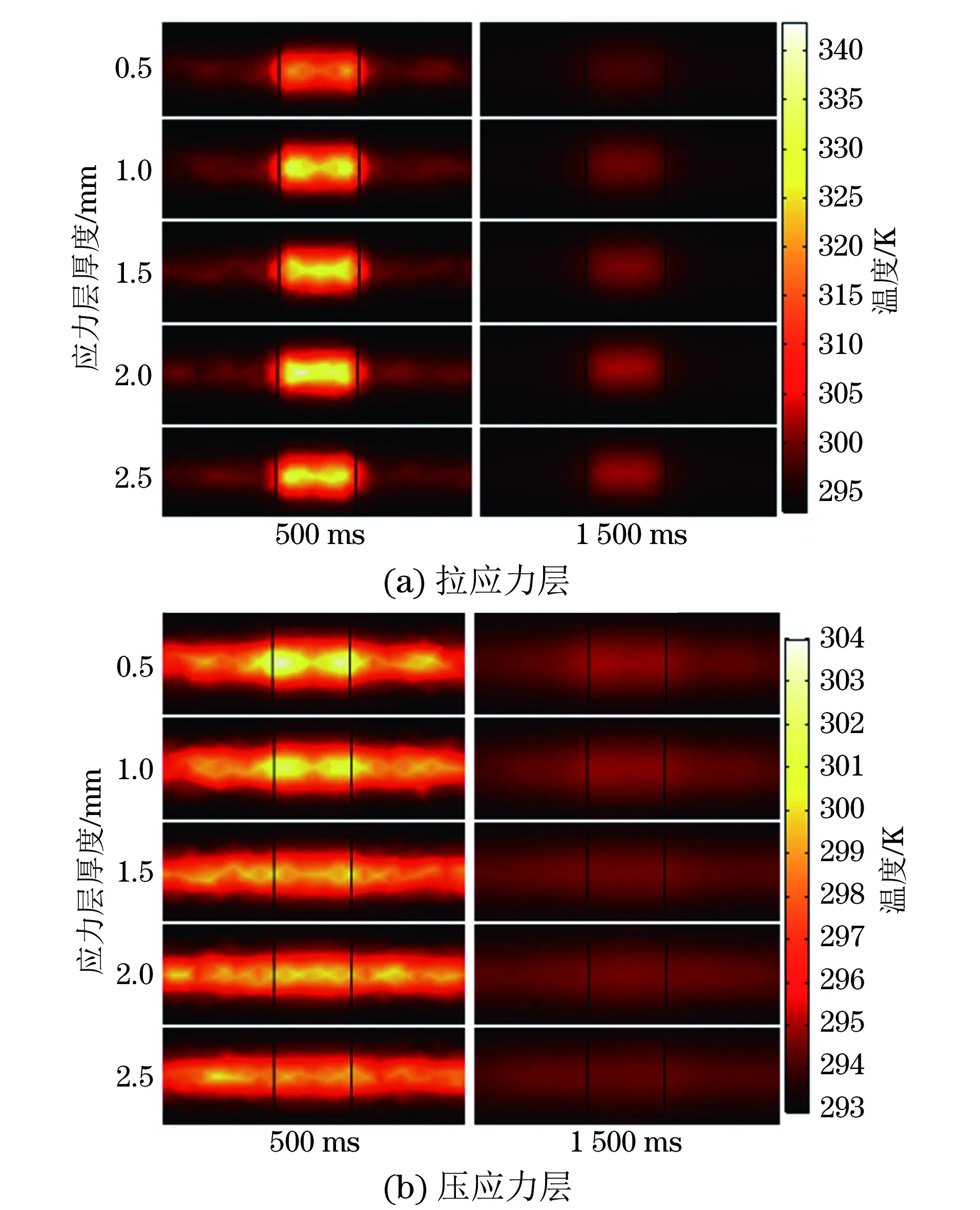
圖8 應(yīng)力層厚度變化對導體表面溫度分布的影響

類比裂紋缺陷深度的影響，研究導體應(yīng)力層的厚度改變時，其表面溫度響應(yīng)曲線的變化規(guī)律,正常區(qū)域、拉應(yīng)力層以及壓應(yīng)力層的電導率分別設(shè)置為5.0×106,2.0×106,8.0×106S·m-1。則由式(5)可計算得到冷卻階段結(jié)束時模擬拉、壓應(yīng)力層的熱擴散深度分別為2.68,5.35 mm。因此，模擬應(yīng)力層的厚度不能超過2.68 mm。在仿真分析時，將最大應(yīng)力層厚度設(shè)置為2.5 mm，應(yīng)力層厚度從0.5 mm開始,以0.1 mm為增量逐漸疊加。應(yīng)力層厚度變化對導體表面溫度分布的影響如圖8所示。

由圖8可見，拉應(yīng)力層厚度越大時，靠近應(yīng)力區(qū)的感應(yīng)渦流越多、越集中，因此應(yīng)力層表面溫度分布越集中，最大溫度值越大；相反，壓應(yīng)力層厚度增大時，感應(yīng)渦流逐漸向正常區(qū)域靠近，應(yīng)力層表面溫度分布越分散，最大溫度值越小。對應(yīng)應(yīng)力層厚度變化時，在加熱結(jié)束及冷卻結(jié)束時點1處的溫度值均相應(yīng)發(fā)生變化，如圖9所示。因此可以通過導體應(yīng)力層表面溫度的變化來反演應(yīng)力層的厚度值。

圖9 不同應(yīng)力層厚度對應(yīng)點1處的溫度響應(yīng)曲線

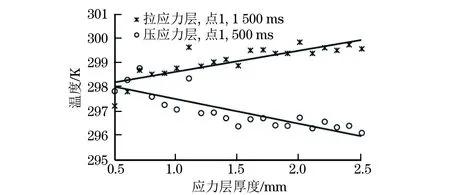
圖10 應(yīng)力層厚度對點1處溫度值的影響

由圖8,9可以看出，拉應(yīng)力層在冷卻階段結(jié)束時的溫度隨厚度的變化明顯，而壓應(yīng)力層在加熱結(jié)束時的溫度隨厚度的變化明顯，在加熱結(jié)束時模擬壓應(yīng)力層的熱擴散深度已達到3.1 mm，大于最大厚度2.5 mm，因此后續(xù)探究應(yīng)力層厚度與溫度變化之間的關(guān)系時，拉應(yīng)力選取冷卻階段結(jié)束時的數(shù)據(jù)，壓應(yīng)力層選取加熱結(jié)束時的數(shù)據(jù)。應(yīng)力層厚度對點1處溫度值的影響如圖10所示，導體應(yīng)力區(qū)域應(yīng)力層厚度與表面溫度近似為線性函數(shù)關(guān)系。拉應(yīng)力層厚度越大，其表面溫度就越高；壓應(yīng)力層厚度越大，其表面溫度就越低。

4 結(jié)論

討論了渦流熱成像法檢測應(yīng)力的原理，建立了數(shù)值仿真模型，利用多物理場耦合的有限元方法，分析了導體應(yīng)力層厚度及電導率、熱導率大小變化對表面不同區(qū)域點的溫度響應(yīng)曲線的影響，根據(jù)仿真結(jié)果，給出了應(yīng)力大小及應(yīng)力層厚度變化與溫度之間的關(guān)系。

(1) 在一定范圍內(nèi)，導體應(yīng)力值與其表面檢測溫度近似為線性關(guān)系，即可以通過導體表面各點的溫度變化情況反演得到導體表面應(yīng)力的大小。若導體表面存在拉應(yīng)力，則應(yīng)力區(qū)的溫度將高于正常區(qū)的，且拉應(yīng)力越大，應(yīng)力層的溫度越高；若導體表面存在壓應(yīng)力，則應(yīng)力區(qū)的溫度將低于正常區(qū)的，且壓應(yīng)力越大，應(yīng)力層的溫度越低。

(2) 在已知應(yīng)力值大小的條件下，導體應(yīng)力層厚度與其表面檢測溫度近似為線性函數(shù)關(guān)系，拉應(yīng)力層越厚，對應(yīng)表面溫度越高；壓應(yīng)力層越厚，對應(yīng)表面溫度越低。即可以通過溫度值的大小來分別確定拉、壓應(yīng)力層厚度。