基于交替起振光電振蕩器的大量程高精度絕對距離測量技術*

謝田元 王菊 王子雄 馬闖 于洋 李天宇 方杰 于晉龍

(天津大學電氣自動化與信息工程學院,天津 300072)

1 引 言

大量程、高精度的絕對距離測量在工業制造、科學研究、航空航天等領域發揮了重要的作用,如大型零件的裝配、星間測距[1?3]等.傳統的絕對距離測量方法分為飛行時間法和干涉法.飛行時間法是通過測量光往返經過待測距離的時間來測量距離,適合長距離的測量,但受到時間測量精度的限制,測量分辨率限制在了毫米量級[4].干涉法(如多波長干涉法、掃頻干涉法[5?8]等)是通過多個波長形成合成波長鏈并逐級精化,或調頻光經過目標反射與本振光拍頻干涉,可以實現納米量級的距離測量,但測量范圍受到模糊距離的限制,一般為幾十米.近年來,通過采用光學頻率梳技術,進一步提高了測距的工作范圍和測量精度[9?14].如Lee等[10]在2010年提出的基于飛秒光脈沖的飛行時間測距方法,在大氣條件下、0.7 km的待測距離上,阿侖方差達到117 nm.Zhu等[13]在2018年提出的基于合成波長雙頻梳干涉測距方法,將飛行時間法、多波長干涉以及載波干涉法與頻率梳相結合,在1.5 m的長度上,測量精度達到亞納米量級.從大的方面來看,上述方法都是通過提高測量系統分辨率來提高測量精度,對測試系統的要求較高,其測量精度和測量范圍的提高受到一定的限制: 如這些方法的高精度距離測量量程較短,通常在百米量級[5?14].

測量中常采用的另一種原理是積累放大的原理,即通過放大被測量來提高測量精度,此方法對可以在較低系統的分辨率的條件下獲得更高的測試精度.在大量程高精度的絕對距離測量方面,光電振蕩器(optoelectronic oscillator,OEO)方案就采用了積累放大原理[15]: 其基本測量原理是將待測距離作為OEO腔長的一部分,利用其振蕩頻率和腔長的變化關系來獲得長度信息; 振蕩器工作在高階諧波振蕩條件下,實現積累放大; 光電振蕩器的腔長一般在km量級,可以實現大量程的高精度距離測量[15,16].但由于振蕩頻率反映的是整個振蕩回路的腔長變化,而整個振蕩回路包含了待測的距離和振蕩器固有的長度,如何分離二者的變化從而得到真實的待測距離就成了該方法的技術難點.在文獻[15,16]中,通過搭建兩個OEO,將待測距離置于其中一個OEO的環路中,構成測量環路; 另一路和測量環路共用除待測距離外的振蕩環路,構成參考環路.此時待測距離即為兩個OEO腔長的差值.實驗結果表明此方案在等效距離為6 km范圍內,相對測量精度達到2.5 × 10–10.但需要指出的是此方案為了保證測量精度的準確性,采用了鎖相環控制光纖拉伸器的方法對參考環路進行腔長控制.這需要多個拉伸量和精度不同的光纖拉伸器以及復雜的控制算法才能實現μm量級的控制精度,從而增加了系統的復雜性,限制了此方案的應用.此外,由于振蕩器的特性,此方案中測量環和參考環并非嚴格共用除測量長度外的所有振蕩環路,即兩路腔長存在非公共部分.這意味著即使鎖定了參考環路,測量環路中的非公共部分仍然存在慢漂,造成誤差.為了擺脫腔長控制對整個測量系統的限制,同時消除兩腔非公共部分慢漂對測量系統的影響,我們提出了基于交替起振光電振蕩器的絕對距離測量方法.

本方法的主要思路是: 通過光開關實現測量/參考OEO間的切換,實現二者交替起振,此時除了被測長度外的兩個振蕩環路完全一致.當切換速度足夠快時,可認為兩個腔的共用部分是時不變的.通過頻率計依次記錄測量/參考光電振蕩器的振蕩頻率計算出測量/參考環的長度.測量的兩個環的長度差即為待測距離.此外,本方案還通過切換微波開關實現高階/低階振蕩模式的切換以進行腔長的粗測.

本方案由于每次距離測量都重新測量參考OEO的腔長,因此不需要考慮由于測量/參考OEO的慢漂帶來的誤差積累,所以參考OEO的腔長也不需要控制,從而簡化了系統.文中對此方案進行了理論分析和實驗驗證.實驗結果顯示在等效6 km的空間往返光路上,相對測量精度達到5.8 × 10–10.

2 方案的理論分析

基于交替起振光電振蕩器的絕對距離測量系統框圖如圖1所示.激光器、強度調制器、光開關、長光纖、光電探測器、放大器、微波開關、濾波器、電耦合器等構成了基本光電諧振腔.其中,激光器波長為1550 nm,輸出功率100 mW; 強度調制器的帶寬為20 GHz; 光開關是2 × 2高速磁光開關,切換速度為30 μs,在實驗中用于兩個振蕩環的切換; 光延時線的量程為330 ps,最小步進為0.3 μm(General Photonics公司的MDL-002),主要用于模擬待測距離變化,驗證測量精度; 長光纖為5 km普通單模光纖; 光電探測器的帶寬為30 GHz; 微波開關為DC-20 GHz單刀雙擲微波開關,用于改變振蕩器的振蕩頻率; 帶通濾波器的中心頻率為9.9 GHz,帶寬10 MHz; 低通濾波器帶寬為100 MHz;微波移相器為機械式微波移相器; 40 kHz—38 GHz寬帶的微波放大器(SHF 806E)用于放大高頻和低頻信號.光延時線置于光開關IN2端口和OUT2端口之間作為待測距離.當光開關處于交叉狀態時,光延時線接入OEO環路,與其他部分構成測量環,定義為OEO1,如圖1(a)所示; 當光開關處于平行狀態時,構成參考環,定義為OEO2,如圖1(b)所示.通過切換光開關可以實現OEO1與OEO2間的切換.帶通濾波器置于電耦合器1的A端口和微波開關的A端口,低通濾波器和移相器置于電耦合器1的B端口和微波開關的B端口.通過微波開關在A,B端口切換可以實現高階模式和低階模式起振頻率的切換.

根據OEO起振的原理[17],其基頻fb與OEO的腔長L的關系為

其中,c為真空中光速,n為光在介質中的折射率(在光纖中,n≈1.5).通常,OEO在高階模式上起振,起振頻率fhm在幾GHz至幾十GHz,由OEO中窄帶濾波器的中心頻率決定.fhm與fb的關系為fhm=Nhm·fb,其中Nhm為高階振蕩模式數(Nhm為整數).根據積累放大原理[15,16],我們可以通過測量OEO的高階振蕩頻率fhm和振蕩模式數Nhm來反推出精確的fb,實現大量程、高精度的長度測量.以我們的實驗條件為例: 光纖長度5 km,光纖折射率n=1.5的條件下,起振頻率fhm在9.9 GHz附近,線寬可達mHz量級[18].此時基頻fb約為40 kHz,Nhm約為2.475 × 105.fhm只需測到Hz量級,頻率測量就達到10–10的精度,根據正確的Nhm值反推出fb也在10–10量級.因此,測量精度取決于fhm的測量準確性和Nhm值的正確性.

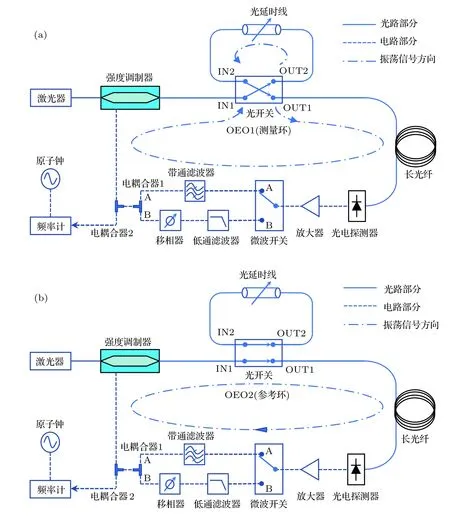
圖1 基于交替起振光電振蕩器絕對距離測量的基本結構(a)光開關處于交叉狀態,測量環振蕩;(b)光開關處于平行狀態,參考環振蕩Fig.1.Basic structure of absolute distance measurement method based on alternately oscillating OEO:(a)The measurement loop oscillates with optical switch at cross state;(b)the reference loop oscillates with optical switch at parallel state.

由于Nhm為整數,Nhm通過粗測基頻fb*來得到,Nhm通過下式計算:

其中,[ ]為四舍五入取整運算,粗測的基頻fb*為相鄰起振模式的頻率間隔.在保證Nhm的正確性條件下,fb*測量值的范圍應滿足測量精度要求在內.在我們的實驗條件下,此fb*的精度要求在 ± 0.08 Hz以內.在高階模式起振時(9.9 GHz),頻率計對fhm的測量精度在Hz量級,無法直接得到符合精度要求的fb*.這時,需要降低起振頻率,以提高頻率的測量精度.方案中我們設置了微波開關,通過切換到B端口選擇低通濾波器,就可以讓OEO在低階模式上振蕩.當振蕩頻率flm低于100 MHz,頻率計的測量精度很容易達到0.01 Hz,滿足對基頻進行粗測的要求.低階模式振蕩頻率flm滿足flm=Nlm·fb關系,Nlm為低階振蕩模式數(Nlm為整數).由于OEO每次在低階頻率起振時,其可能在通帶內的任意模式上起振,起振模式間的頻率差為諧振腔基頻fb的整數倍,最小頻率間隔即為fb.連續測量起振頻率可以得到一系列頻率差Dflmi.將[Dflmi]kHz定義為Dflmi精確到kHz后的整數值,求得[Dflmi]kHz的最大公約數定義為fGCD.該最大公約數即為精確到kHz的最小跳頻間隔.則各頻率差對應的模式間隔數DNlmi表示為DNlmi=[Dflmi]kHz/fGCD.因此各測量時刻的基頻f'b表示為f'b=Dflmi/DNlmi.由于不同模式的振蕩頻率在不同時刻測得,受到環境影響,f'b與fb并不嚴格相等.但只要兩次測量的腔長變化在以內,計算得到的Nhm的正確性就不會受到影響.在我們的實驗條件下,腔長差應保證在 ± 10 mm以內.在溫度變化不大、測量時間較短的情況下是很容易達到的.根據f'b與flm可以確定低階振蕩模式數Nlm,進而得到粗略測量的fb*.Nlm和fb*分別用(3)和(4)式計算得到:

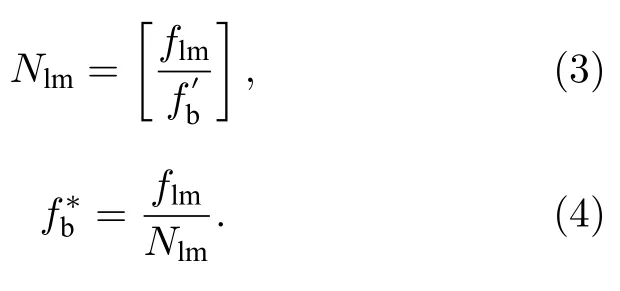
需要注意的是,直接用低通濾波器替代窄帶濾波器會導致微波電路部分的時延不同.從前面的分析可知: 為了使低階模式下計算得到的fb*可以直接代入高階模式時的fb*,兩部分電路的長度差也要控制在 ± 10 mm以內.這可以利用矢量網絡分析儀測量并調整微波移相器實現.

最終OEO腔長L的計算公式如下:

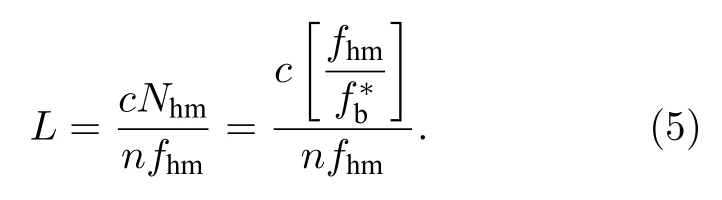
為了模擬空間中大量程距離測量的情況,我們用km量級的長光纖代替真實的空間待測距離.理論上,該長光纖應置于光開關IN2端口和OUT2端口之間.但長光纖容易受環境影響導致光纖長度變化,此變化量無法精確預知,也就無法對系統的測量精度進行校準和評價.為此,不失一般性,將這部分光纖置于OEO1和OEO2的公共部分,這樣一方面保證了測試系統的長諧振腔與大量程測量系統的一致性,另一方面也保證了對系統測量精度的精確評估.

如上所述,在一個完整的測量過程中,光開關和微波開關依次切換,系統處于4個不同測量狀態: 高階諧振條件下測量測量環、低階諧振條件下測量測量環、高階諧振條件下測量參考環、低階諧振條件下測量參考環.定義OEO1在高階和低階模式起振的頻率和振蕩模式數分別為fhm1,Nhm1和flm1,Nlm1; OEO2在高階和低階模式起振的頻率和振蕩模式數分別為fhm2,Nhm2和flm2,Nlm2.光開關所處狀態和微波開關的切換順序以及fhm1,flm1,fhm2,flm2的測量順序如圖2(a)所示.在t1i,t2i,t3i,t4i,t1i+1,t2i+1,t3i+1,t4i+1…時刻切換微波開關; 在t1i,t3i,t1i+1,t3i+1…時刻切換光開關狀態; 開關切換后依次測量fhm1i,flm1i,fhm2i,flm2i,fhm1i+1,flm1i+i,fhm2i+1,flm2i+1,….根據(5)式,對應的OEO1和OEO2的腔長依次為L1i,L2i,L1i+1,L2i+1,…,如圖2(b)所示.

當分別得到測量環和參考環的腔長后,待測的距離就是二者的差.但是由于測量時刻不同,腔長的時變特性會影響測量的精度.在我們的實驗中,考慮到溫度等影響因素的瞬時變化率很小,不存在跳變,可以認為短時間內腔長變化是近似線性的,因此,t3i時刻測量的OEO1腔長近似表示為L1i和L1i+1的平均值此時,OEO2的腔長為L2i.t3i時刻,OEO1和OEO2的腔長差即為待測距離D2i,表示為:

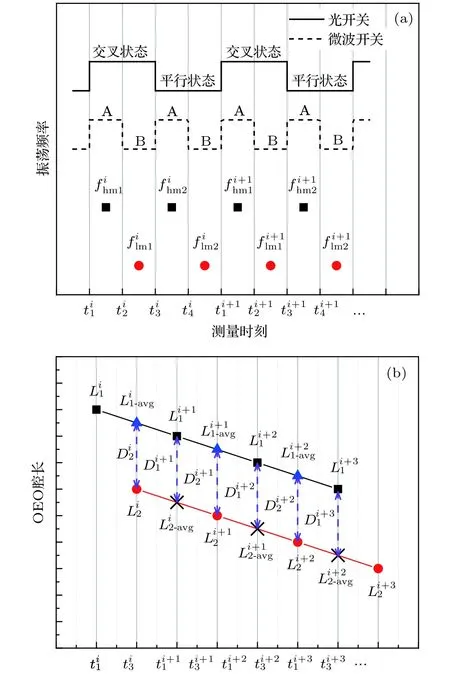
圖2 距離測量過程(a)光開關、微波開關切換時刻及相應的頻率測量;(b)OEO1和OEO2的腔長測量及絕對距離測量Fig.2.Distance measurement process:(a)The switching moments of optical switch and microwave switch and corresponding frequency measurement process;(b)loop length measurement of OEO1,OEO2 and the absolute distance measurement.

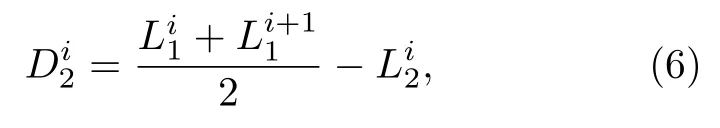
同理,也可以得到t1i+1時刻的待測距離D1i+1表示為:

最終的待測距離測量過程如圖2(b)所示.

3 實驗系統及測量結果

在實驗中,首先采用了5 km的光纖(等效于7.5 km的空間距離)進行測試.頻率計測量一次過程如圖3所示.0—25 ms,光開關處于交叉狀態、微波開關切換到A位置,OEO1在高階模式起振;25—125 ms,頻率計記錄fhm1; 125—150 ms,光開關處于交叉狀態、微波開關切換到B位置,OEO1在低階模式起振; 150—250 ms,頻率計記錄flm1; 250—275 ms,光開關處于平行狀態、微波開關切換到A位置,OEO2在高階模式起振;275—375 ms,頻率計記錄fhm2; 375—400 ms,光開關處于平行狀態、微波開關切換到B位置,OEO2在低階模式起振; 400—500 ms,頻率計記錄flm2.

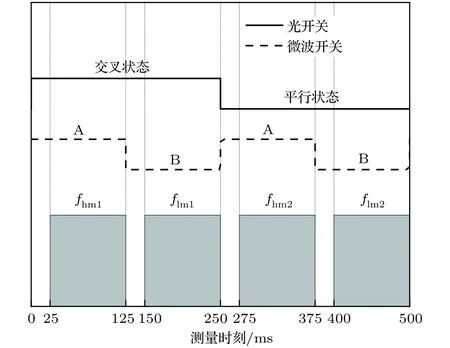
圖3 開關切換及頻率計計數時序圖Fig.3.The switching time and frequency counting timing diagram.

OEO在高階、低階模式起振時產生的微波信號的頻譜分別如圖4(a)和圖4(b)所示.電譜儀(Agilent 8564 EC)的頻寬(SPAN)設置為200 kHz,帶寬分辨力(RBW)設置為3 kHz.從圖4(a)和圖4(b)可以看出,OEO產生的微波信號邊模約為40 kHz,且測量/參考環在高階/低階模式振蕩時,邊模抑制比均大于40 dB.雖然沒有文獻[15]中采用雙環光電振蕩器結構的邊模抑制比高,但40 dB的邊模抑制比并不影響頻率計的正常工作,因此對系統的測量精度沒有影響.

測量過程中,為了保證頻率測量的準確性,頻率計以銣原子鐘作為時間基準,實驗采用的銣原子鐘的長期頻率穩定度為5 × 10–12,頻率計的門控時間設置為100 ms.OEO起振在高階和低階模式時,頻率計的頻率分辨率分別為1 Hz和0.01 Hz.光延時線在0 mm位置時,頻率計連續測量10次,結果如圖5(a)所示.OEO1和OEO2的高階起振頻率fhm1和fhm2分別用方形點和圓點表示,可以看出,fhm1和fhm2起振在9.906 GHz附近,測試過程中存在跳模現象,分別跳變了7次和5次(如虛線所示).OEO1和OEO2的低階起振頻率flm1和flm2分別用三角形點和 × 形點表示,可以看出,flm1和flm2起振在69 MHz附近,且分別發生了7次和6次跳模(如虛線所示地).經計算,測量環的fGCD為40 kHz,flm1在第3次和第4次測量時的跳模頻率間隔為最小跳模間隔.根據各測量時刻的頻率差以及fGCD可以得到各測量時刻的f'b.將f'b以及相應時刻測量的flm1代入(4)式計算得到各測量時刻的fb1*,約為39818.14 Hz.同理,可以得到fb2*約為39831.73 Hz.

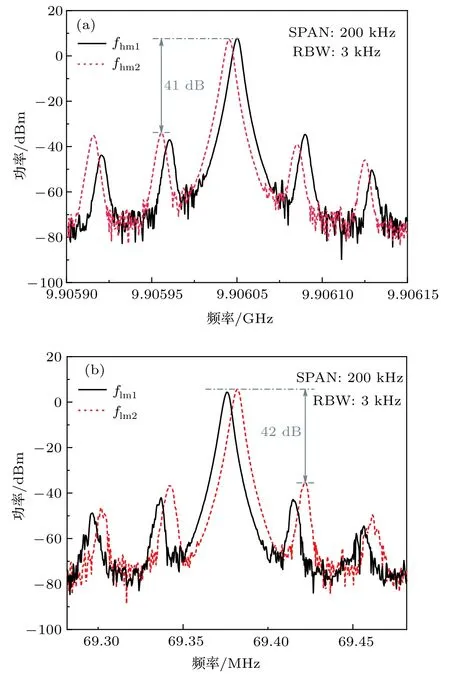
圖4 測量/參考環振蕩信號的頻譜圖(a)高階模式起振;(b)低階模式起振Fig.4.RF spectrum of oscillating frequencies of measurement/reference loop:(a)With OEO oscillating at high-order mode;(b)with OEO oscillating at low-order mode.

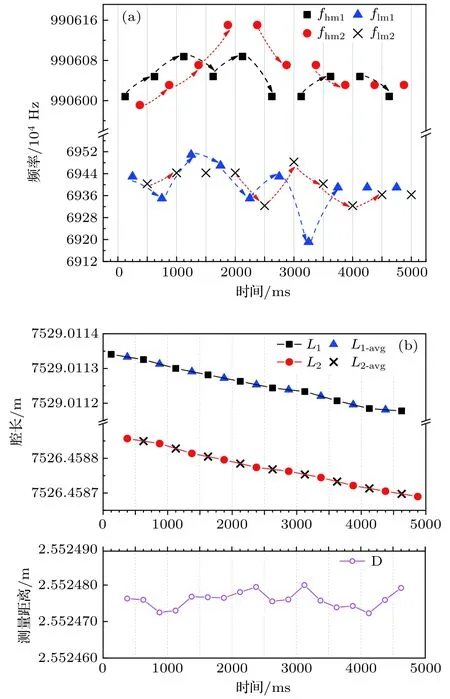
圖5 長光纖為5 km光延時線在0 mm位置時的測量結果(a)OEO1和OEO2起振頻率測量值;(b)OEO1和OEO2的腔長及待測距離測量結果Fig.5.Measurement results at 0 mm position of optical delay line with 5 km fiber:(a)Oscillating frequencies of OEO1 and OEO2;(b)loop lengths of OEO1 and OEO2,and distance measurement results.

將各測量時刻的fb1*和fb2*代入(5)式,可以得到OEO1和OEO2的腔長,并計算相鄰腔長的平均值.如圖5(b)所示,OEO1和OEO2的腔長分別用方形點和圓點表示,相鄰腔長的平均值分別用三角形點和 × 形點表示.待測距離為對應時刻OEO1和OEO2腔長的差值,用空心圓表示.可以看出,OEO1和OEO2的腔長在測量過程中分別從7529.011341 m和7526.458857 m逐漸減小為7529.011177 m和7526.458690 m; 而待測距離趨于定值,平均值為2.552476 m,標準差為2.7 μm.

為了進一步驗證所提方案的正確性,將光延時線從初始位置位移8次,每次位移為10 mm,延時線位移誤差小于0.3 μm.按照上述方法,對光延時線的每個位置進行距離測量,每個位置測量/參考OEO的高階/低階連續測量10次,得到18個測量距離.將18個測量距離取平均后作為測量結果與光延時線的位移距離進行比較,結果如圖6所示.光延時線位移距離與測距結果用方形點表示,有很好的線性關系.測距結果與光延時線各位移距離的誤差用三角點表示,誤差線表示為每個測量距離的標準差.可以看出,在7.5 km的空間距離上,在整個測量范圍內誤差為4.2 μm,每個測量距離的標準差均小于4 μm,相對測量精度為5.6 × 10–10.等效成實際應用的往返測量時,就是測量范圍為3.75 km,誤差與標準差相應減半,相對測量精度不變.

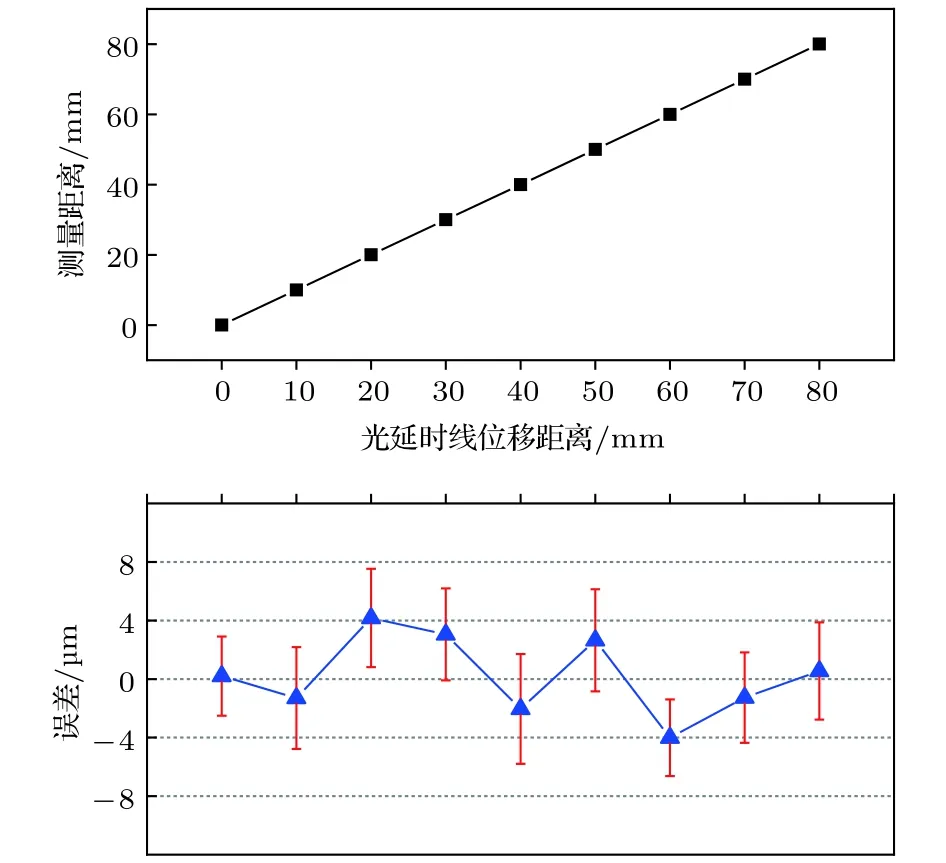
圖6 長光纖為5 km時測量距離與光延時線位移距離的關系Fig.6.The relationship between measured distance and position variation of optical delay line with 5 km fiber.

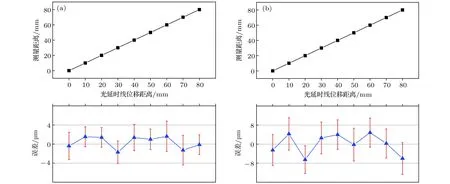
圖7 測量距離與光延時線位移距離的關系(a)1 km長光纖;(b)8 km長光纖Fig.7.The relationship between measured distance and position variation of optical delay line:(a)With 1 km fiber;(b)with 8 km fiber.

為了驗證系統的工作范圍,我們將5 km長光纖分別替換為1 km和8 km的長光纖,來模擬0.75 km和6 km的空間往返距離.測量距離與光延時線位移的關系分別如圖7(a)和圖7(b)所示.通過分析可以得到,等效往返待測距離0.75 km(1 km長光纖)時,整個測量范圍內誤差為1 μm,每個測量距離的標準差均小于1.8 μm,相對測量精度為1.3 × 10–9; 等效往返待測距離6 km(8 km長光纖)時,整個測量范圍內誤差為3.5 μm,每個測量距離的標準差均小于3.5 μm,相對測量精度達到5.8 × 10–10.

以上結果是在現有的實驗條件下取得的,考慮到以下因素,本方案還有進一步改善的空間: 1)由于實驗條件的限制,本實驗的長光纖并沒有放在測量距離上,而在實際應用當中,待測距離會存在于測量OEO中而不是在公共部分,因此公共部分長度很短,受環境的影響更小; 2)實驗中所使用的光開關是光纖耦合結構,如果做成空間結構,光路帶來的誤差將會更小; 3)如果能夠采用測試速率更高的頻率計也能進一步提高系統的測量精度.

4 結 論

本文提出了一種基于交替起振光電振蕩器的大量程、高精度絕對距離測量方法.實驗采用了測量、參考光電振蕩環交替起振、測量的方法.從而有效消除了光電振蕩器自身漂移對測量帶來的不利影響.在保持了OEO測距的大量程、高精度優點的同時,不需要對OEO的腔長進行控制,大大簡化了系統,擴展了系統的可用性.實驗結果表明:在等效6 km的空間往返待測距離上,測量誤差為3.5 μm,每個測量距離的標準差小于3.5 μm,相對測量精度達到5.8 × 10–10.此方法為解決大量程、高精度絕對距離測量技術難題提供了一種可行的思路.