源自弦景觀的有效Quintessence*

2019-08-27 06:57:24翟韓豫申佳音薛迅2

物理學報 2019年13期

翟韓豫申佳音薛迅2)?

1)(華東師范大學物理系,上海 200241)

2)(新疆大學理論物理中心,烏魯木齊 830046)

1 引言

從弦理論約化到描述低能物理的有效場論時,需要將多出來的六個空間維度緊致化到非常小的微觀尺度,這一處理方法被稱之為弦理論的緊致化.在緊致化后,便可以用一個低能有效理論來描述熟悉的四維世界[1,2].弦論有10500種之多的緊致化方案,其中所有不等價的低能有效理論,其真空能的取值形成了一個復雜的“山脈地形圖”,構成了所謂的弦景觀[3].

1998年通過觀測遙遠超新星發現宇宙正在加速膨脹,德西特(de Sitter,dS)型的真空可以解釋宇宙的加速膨脹,但是從弦理論出發,我們很難得到亞穩的dS真空,并且基于dS真空的自洽有效場論都難以與量子引力相容.Vafa等[4,5]在2005年提出了沼澤地的概念,即弦景觀被一個更廣闊的沼澤地所包圍,并非所有的自洽有效場理論都可以從弦理論中導出,有許多看似自洽的有效場理論實際上和量子引力理論并不兼容,不具有紫外完備性,不屬于弦景觀,只能被排除到所謂的“沼澤地”當中.Vafa等提出了兩個擬議的沼澤地判據并研究了其宇宙學含義,指出對于宇宙的后期加速膨脹來說,第二個沼澤地判據(對于任何自洽的量子引力理論的標量勢V,當V>0 時,存在下限|??V|/V>c～O(1),c是正的常數,單位為約化的普朗克單位)與亞穩 dS勢能不相容,但是quintessence類型的勢能以及弦景觀的反德西特(anti-de Sitter,AdS)真空勢能可以與這兩個判據相容[6,7].

在Vafa等提出的“dS沼澤地”猜想中指出:dS空間不存在自洽的量子引力理論,它屬于沼澤地.其直接否定了弦理論中正的穩定真空能的存在,用一個標量場的勢來描述真空能量的話,存在兩種dS類型的標量場勢V[8,9],

1)亞穩態的dS即具有局域極小的勢能類型,如圖1所示.

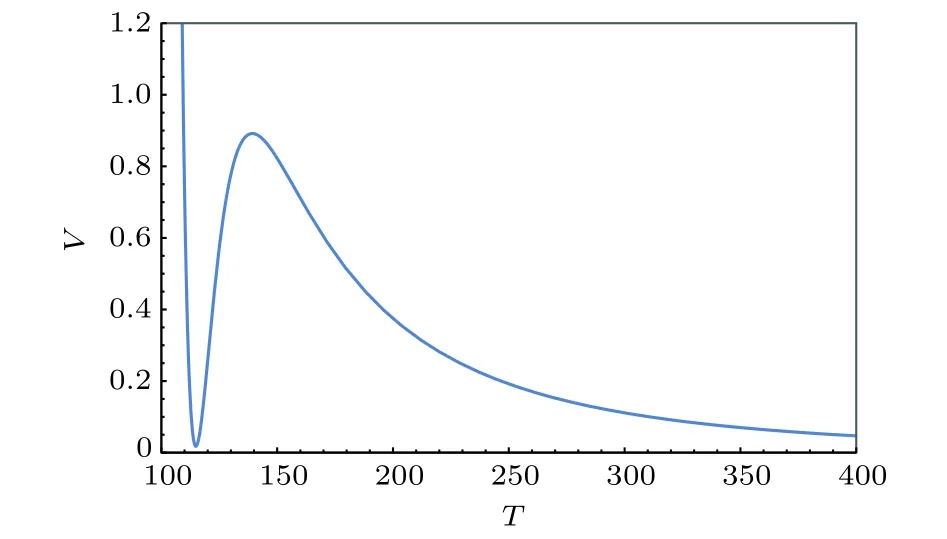
圖1 亞穩態dS的標量勢VFig.1.The scalar potential V for a metastable dS.

2)quintessence場類型即單調下降的勢能類型,如圖2所示.

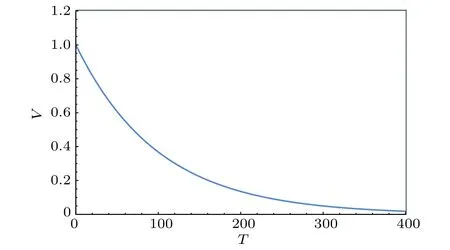
圖2 不穩定dS的標量勢VFig.2.The scalar potential V for an unstable dS.

沼澤地的兩個判據排除了亞穩態的dS時空作為解釋晚期宇宙加速度膨脹的可能性.

洛倫茲不變性是物理學最嚴格的對稱性之一,然而在目前的量子引力理論中,很多模型都指向了洛倫茲對稱性的破缺[10,11].按照現在宇宙學的標準模型,業界相信宇宙首先經歷了量子引力主導的時期,隨后經歷暴脹,暴脹結束后才開始正常膨脹,然后在近期又開始了加速膨脹,現在的可觀測宇宙是由量子引力主導時期的一個非常小的時空區域經歷暴脹所得到的.量子引力的一個普遍的特征是洛倫茲破缺和非局域性,暴脹前洛倫茲破缺的時空區域尺度會隨著早期宇宙暴脹超出視界,在暴脹結束后的某個時間有可能又重新進入視界或者尚未進入視界,洛倫茲破缺時空區域的各個部分因為暴脹被急速拉開遠離,因而失去相互作用,使得洛倫茲破缺被凍結在大尺度上[12].因此,當我們在研究宇宙學問題時需要將大尺度上的洛倫茲破缺效應考慮在內[12?17].

廣義相對論是目前最成功的引力理論[18?20],但是涉及大尺度的天文觀測現象也有許多與單純廣義相對論預言不符合的現象.最困擾物理學界的就是為解釋宇宙加速膨脹而引進的宇宙學尺度上斥力存在的暗能量假說,暗能量最簡單的唯象模型是用宇宙學常數來描述暗能量,也就是所謂的ΛCDM模型.ΛCDM模型的問題在于當我們將宇宙學常數看成真空能量密度時,天文觀測與理論預言之間存在很大差距,理論預言比天文觀測大了54到112個數量級,這就必須使用精細調節機制,理論的置信度就被極大地降低.所以,導致宇宙后期加速膨脹的暗能量機制依然是一個亟待解決的問題.

將考慮了大尺度洛倫茲破缺的引力理論運用到宇宙學,真空能量密度或者等效的宇宙學常數項并非導致宇宙加速膨脹的唯一原因,洛倫茲破缺效應會貢獻一個等效的“暗能量”,兩者綜合在一起的結果會產生觀測到的宇宙后期加速膨脹.真空能量密度有點像一個裸的宇宙學常數,考慮了大尺度洛倫茲破缺效應在內的等效能量密度是決定宇宙演化的有效宇宙學常數或者真空能量密度.暗能量的產生機制是宇宙學中最大的謎題,這方面的研究非?；钴S[21?31],我們從凍結在大尺度上的洛倫茲破缺導致物質的暗伴的角度來思考這一機制是一個全新的視角.這樣我們發現弦景觀中裸宇宙學常數為負時也可以使宇宙產生加速膨脹,并在與ΛCDM模型做對比時,導致一個作為有效真空能量密度的宇宙學常數,其行為對于弦景觀表現為單調下降的類quintessence勢.對于大部分具有裸的正真空能量密度的沼澤地,有效宇宙學常數隨時間的演化會出現局域極小,與單調下降的quintessence勢所導致的演化不符.從而源自弦景觀的真空能量密度會給出滿足沼澤地判據的quintessence勢,而亞穩的dS真空正宇宙學常數的沼澤地模型給出的真空能量密度演化不是quintessence勢,也就不能滿足第二個dS判據.因此導致后期宇宙加速膨脹的有效勢只能來自弦景觀,其自然具有紫外完備性,所以給出了后期宇宙加速膨脹是早期量子引力的特征,從而避免了Vafa等文章中指出的弦沼澤地與后期加速膨脹難以相容的問題.另外基于弦理論,其真空為AdS類型,在用ΛCDM模型解釋宇宙后期加速膨脹時就需要正的宇宙學常數,于是弦理論學家不得不構造一些不自然的模型,將穩定的AdS真空能量密度提升至正值,變成亞穩的dS真空.我們通過考慮大尺度洛倫茲破缺效應,自然地實現了從裸的負真空能量密度提升至正的有效真空能量密度,避免了很多不自然的技術,也避開了沼澤地猜想的第二判據.

2 大尺度洛倫茲破缺下的引力理論

要構造包含大尺度洛倫茲破缺下的引力理論,可以借助規范原理,將局域對稱性加以約束進行破缺[12].為引入局域SO(3)不變洛倫茲boost破缺的約束條件,我們先考察洛倫茲規范勢在局域SO(3)下的變換性質.規范勢在局域洛倫茲變換x7→Λ(x)x下滿足

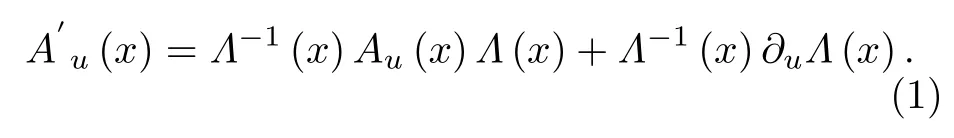
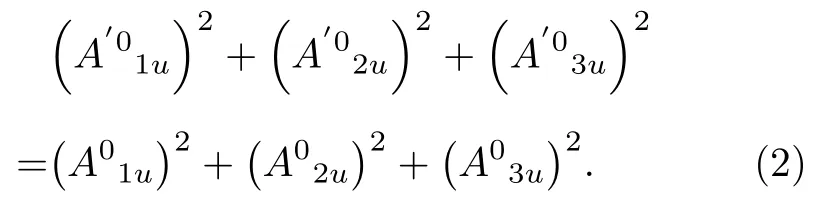
即可得規范勢Au所滿足的約束條件為

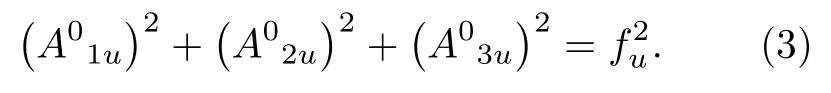
函數fμ(x)可以認為是洛倫茲破缺的量度,并且是參考系依賴的.

在Hilbert-Einstein作用量中加入Lagrange乘子項λu

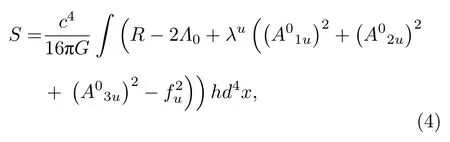
其中Λ0是真空能量密度給出的裸宇宙學常數,R為曲率標量.需要注意的是,由于拉格朗日乘子項的存在,其對聯絡的運動方程的貢獻相當于一個有效的角動量張量,所以即使引力場的物質源是無旋的,聯絡的運動方程也會偏離廣義相對論中的形式,一般的聯絡是有撓的,而非廣義相對論中的Levi-Civita聯絡.

取滿足宇宙學原理的度規假設,即FRW度規的形式

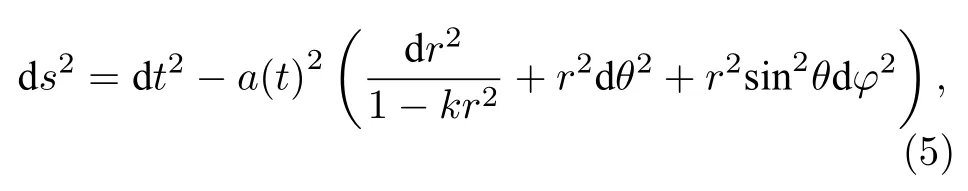
可以讀出瞬時共動標架為

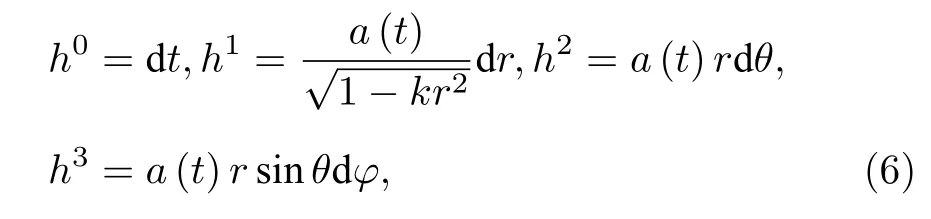
在這個標架下可以將聯絡運動方程和標架的運動方程明確的寫出來.對標架項進行變分可以得到標架運動方程

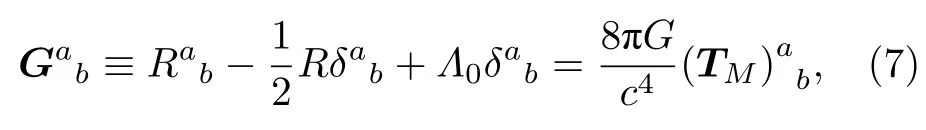
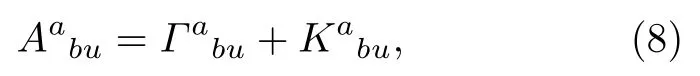
其中Γabu是Levi-Civita項,Kabu是contortion項.

對規范勢的運動方程加上約束條件整理可得

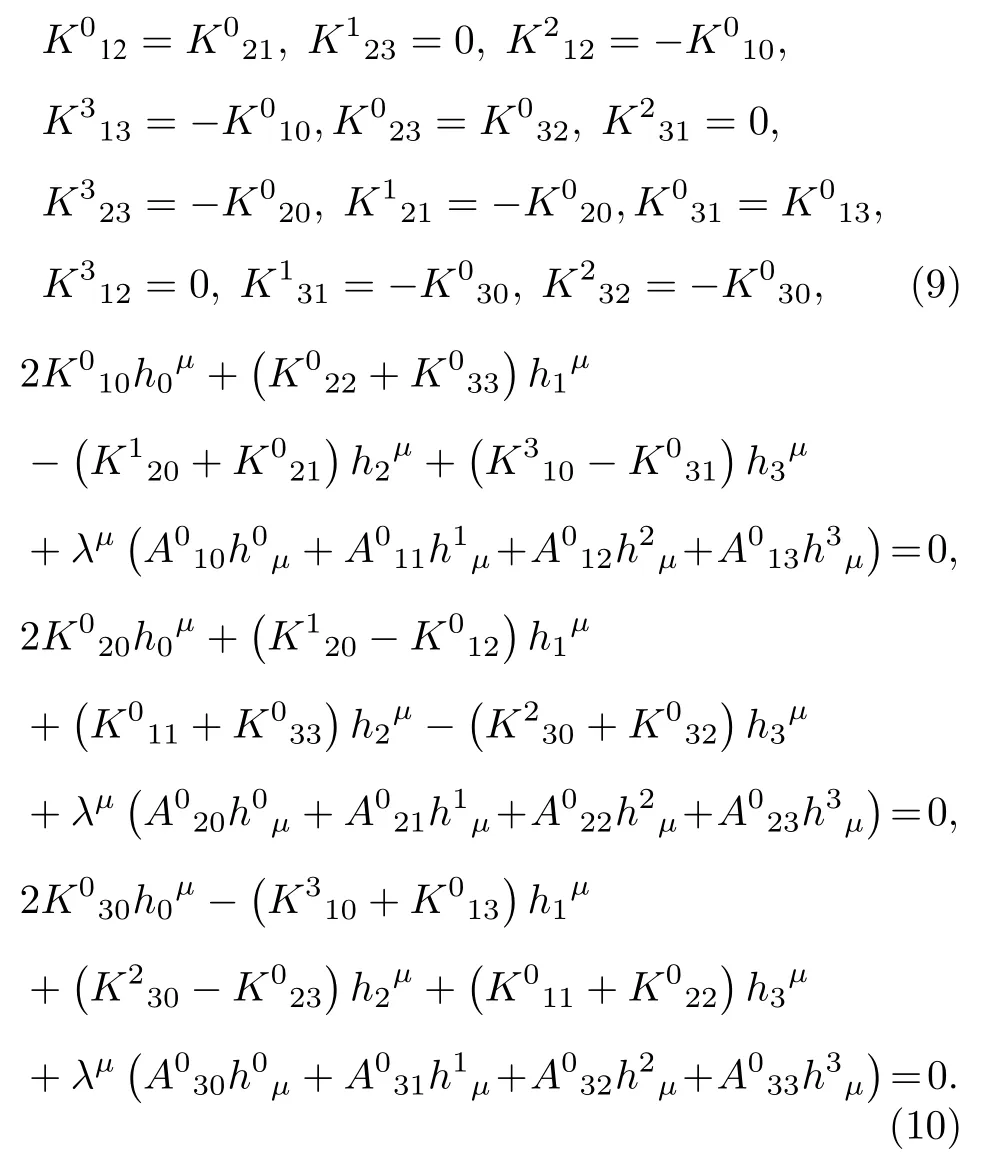
由宇宙學原理,宇宙介質應該是理想流體,其能動張量具有理想流體的特征,由能量密度r和壓強p來描述,即由方程(7)得到必須是對角矩陣,由此可以解出可以非0,其他的contortion分量皆為0.又由于宇宙學原理要求只能是宇宙時t的函數,所以

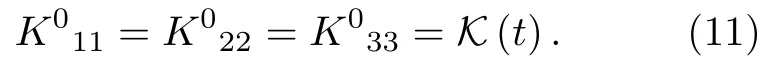
此時,可以給出fμ與K(t)的關系

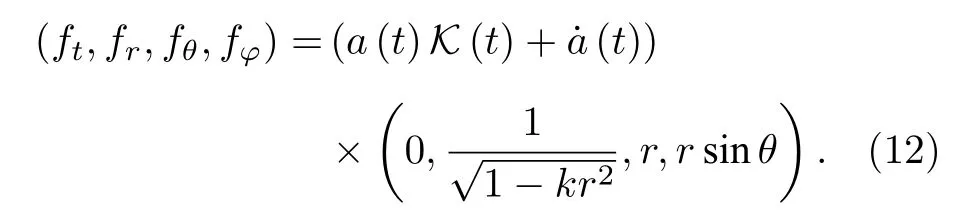
fμ中的三個自由度是由標架的選取而被確定,剩余的一個自由度以K(t)表達.注意到(7)式中的愛因斯坦張量Gab其聯絡Aabu是有撓的,記Aabu的無撓部分Levi-Civita聯絡Γabu所產生的相應幾何量為且

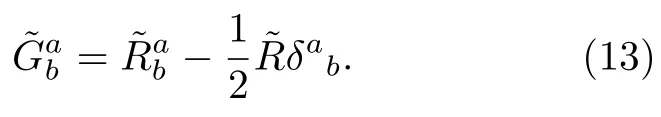
我們可以將(7)式的標架場方程改寫為

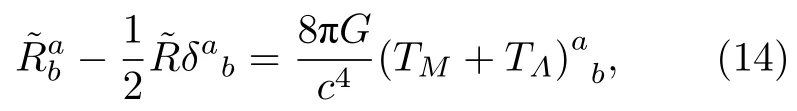
由(7)式,(11)式和(14)式可以得到,對于理想流體暗伴的有效能量動量張量為

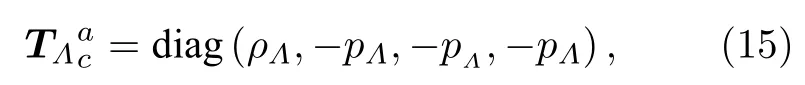
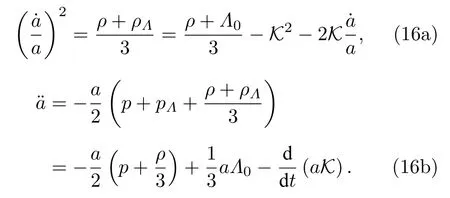
由修正的Friedmann方程(11)可知宇宙的加速膨脹解應該滿足

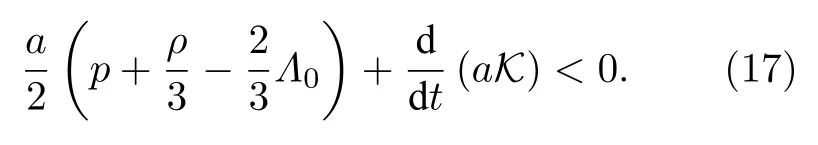
應該注意的是(11)式中的K不能由(11)式確定,即便是給出了宇宙介質的狀態方程.由(12)式可知,K可以用fμ來表示.fμ是我們之前唯象引入的,其演化應該由量子引力和暴脹模型給出,目前的模型不能給出fμ或K的演化,為了確定K的演化規律,我們不得不做一些近似.因為ΛCDM模型是一個非常好的宇宙學唯象模型,可以借助其給出K的演化近似,基于ΛCDM模型的Friedmann方程

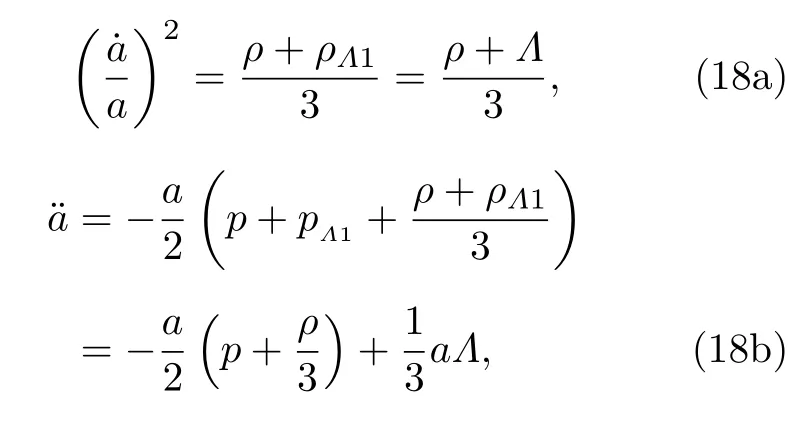
其中ρΛ1=Λ,pΛ1=?Λ.

由(16a)和(18a)式我們可以得到K(t)的初始條件

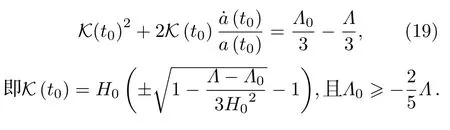
3 三種近似下的模型

第一種近似CaseA:

通過對比(16)式和(18)式,我們可以將K(t)與ΛCDM模型中的宇宙學常數L建立聯系

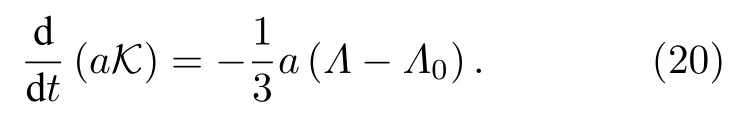
第二種近似CaseB:

宇宙介質的狀態方程p(t)=w(t)ρ(t),代入到(16)和(18)式整理可得

大尺度洛倫茲破缺模型

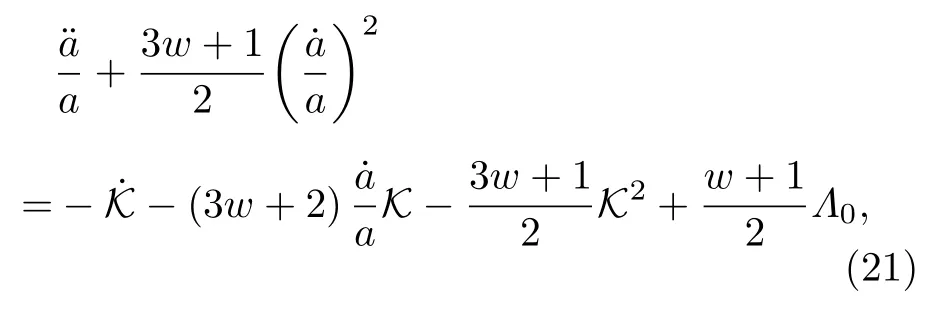
ΛCDM模型

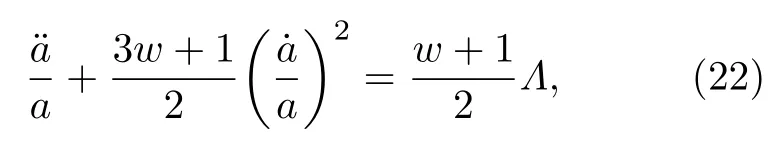
對比(21)式和(22)式可以得到

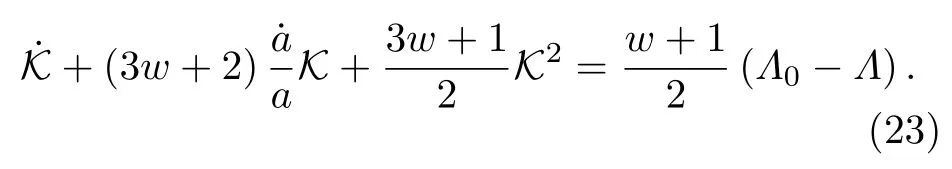
第三種近似CaseC:

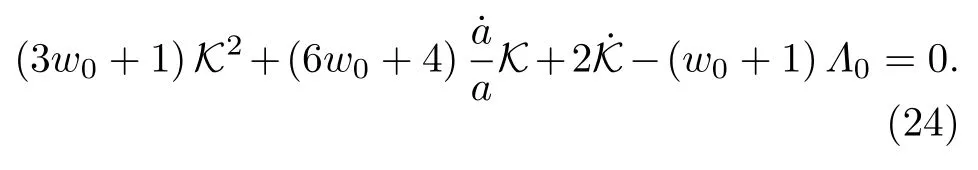
因此將(20),(23),(24)式分別與(16)式結合并有初始條件是宇宙的當今時刻,可以確定K(t)和哈勃參數H(t)的演化.修正的Friedman方程(16)式有兩個不同的解從ΛCDM模型的解來看,第一個解更合理.我們只考慮物質為主的時期即表1對上述情況進行了匯總.

表1 Lorentz破缺宇宙學的幾種模型Table 1.Proposed models of Lorentz violation cosmology.

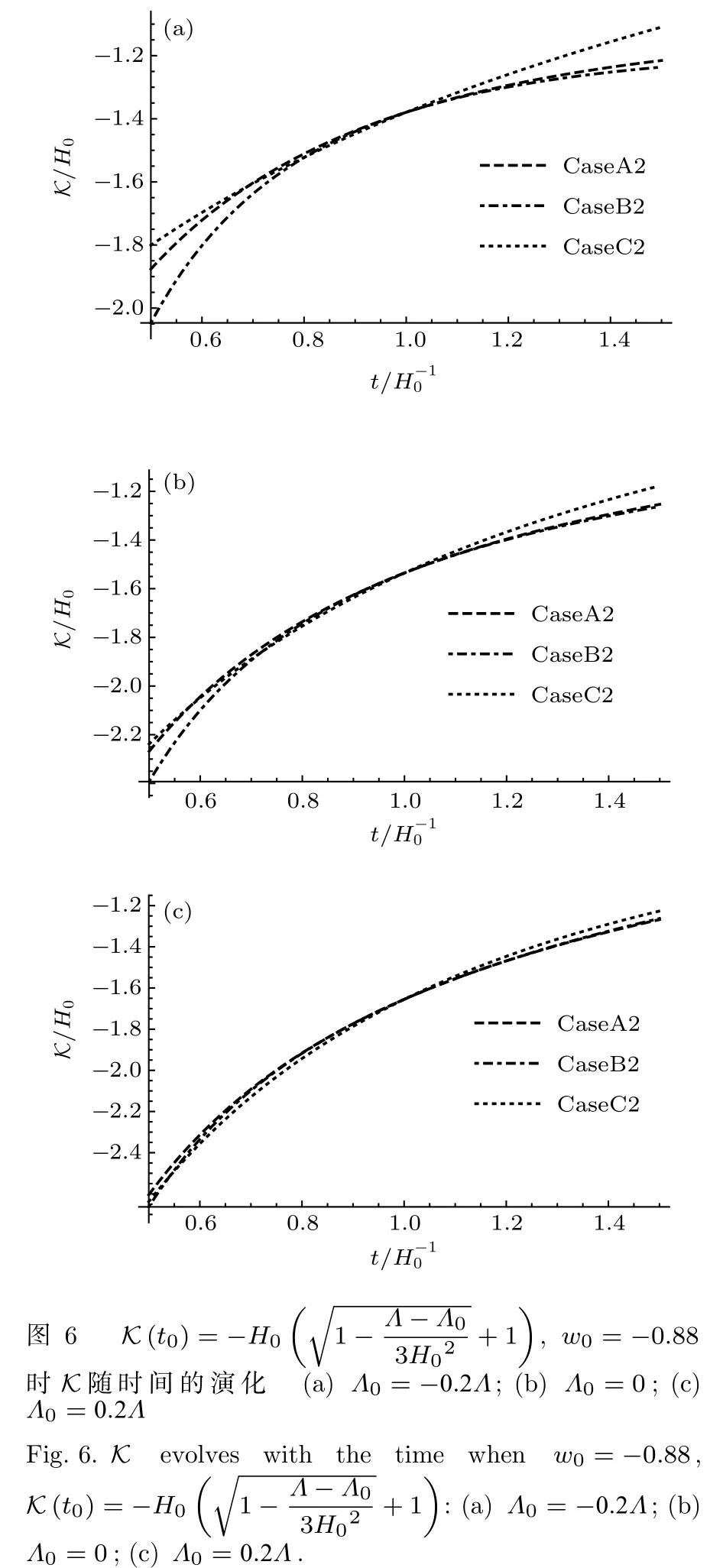
圖3和圖4給出了不同初值下哈勃參數隨著時間的演化曲線.可以看出在哈勃時間附近的范圍內,這幾種模型的宇宙演化非常近似.在長期的演化中,CaseB1與ΛCDM模型的演化結果趨近于完全相同,CaseA1和ΛCDM模型的結果相比要比CaseB1的差別大一些,CaseC1和ΛCDM模型的演化結果相比差別很大,并且隨著Λ0的增大,CaseA1,CaseC1與ΛCDM模型的差別也在逐漸縮小.CaseB2與ΛCDM模型的結果也趨近于完全相同,相比于CaseA1和CaseC1,CaseA2與CaseC2要比ΛCDM模型的演化結果偏差更大.圖5和圖6給出了不同初值下K隨宇宙時的演化曲線,可以看出,CaseA1和CaseB1在哈勃時間附近的范圍內趨近于完全一致,并且在長期的演化過程中也非常相近,CaseC1和CaseA1,CaseB1的演化結果偏離的較大.CaseA2,CaseB2和CaseC2在哈勃時間附近的范圍內也趨近于完全一致,并且在長期的演化過程中CaseC2與CaseA2,CaseB2的偏差比CaseC1與CaseA1,CaseB1的偏差要小.

需要注意的是,在contortion不為零的情況下,光的世界線依然是類光測地線而不是自平行曲線,所以紅移公式與Lorentz不變情況一樣,即

對于k=0,由光度距離的定義[32]可得

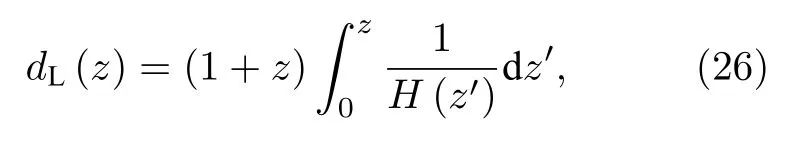
距離模數被定義為[32]

由(25),(26)式可以將(16)和(20),(23),(24)式轉化為以紅移z為變量的K(z)和dL(z)的方程組:

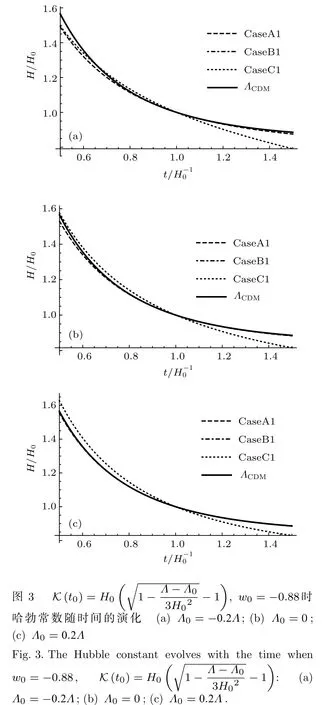
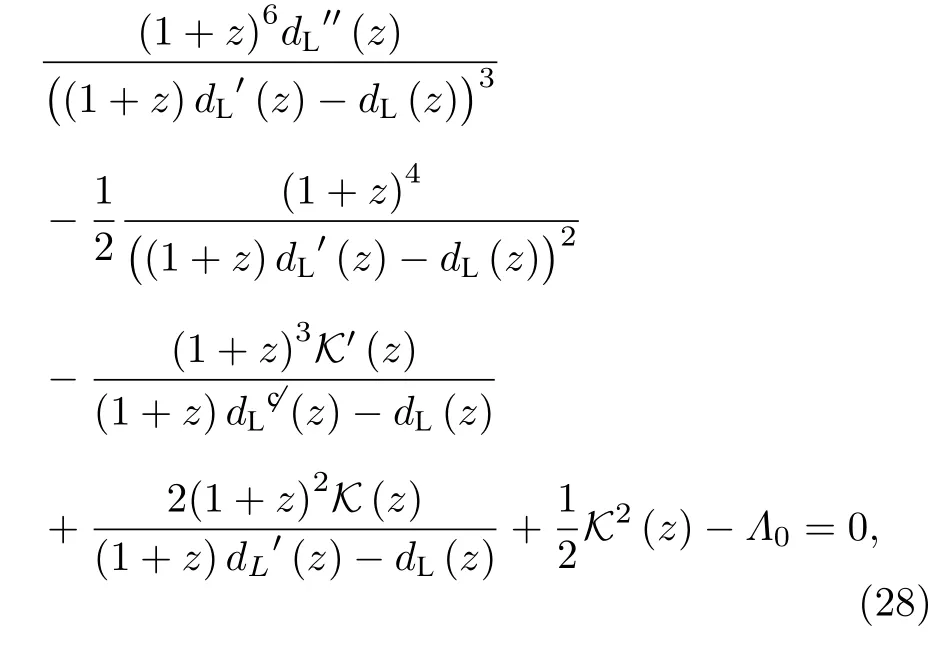
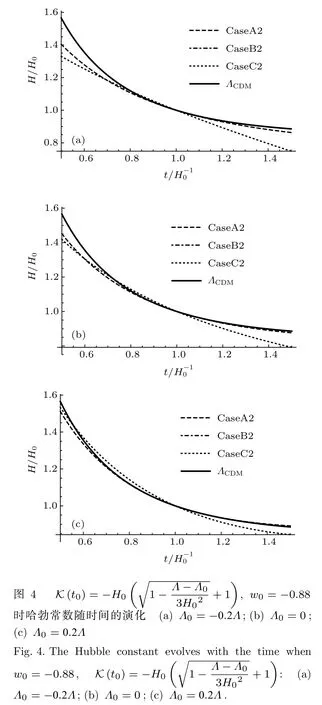
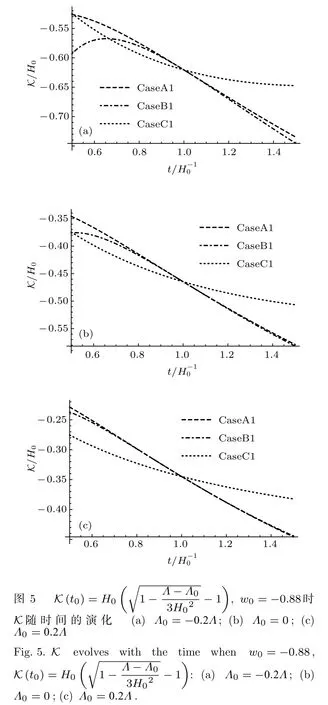
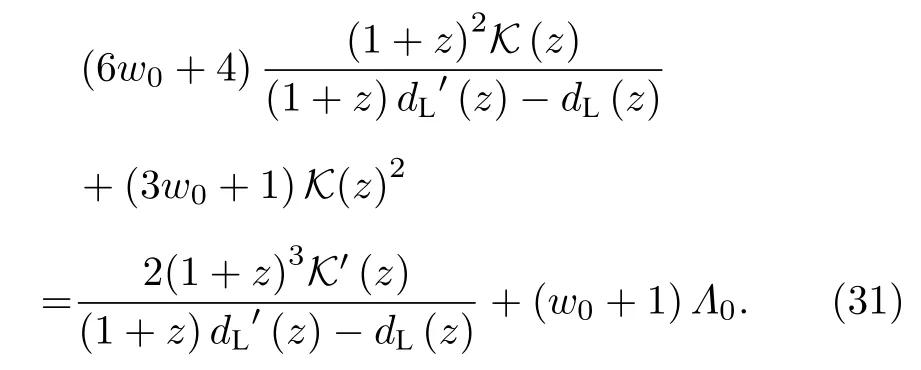
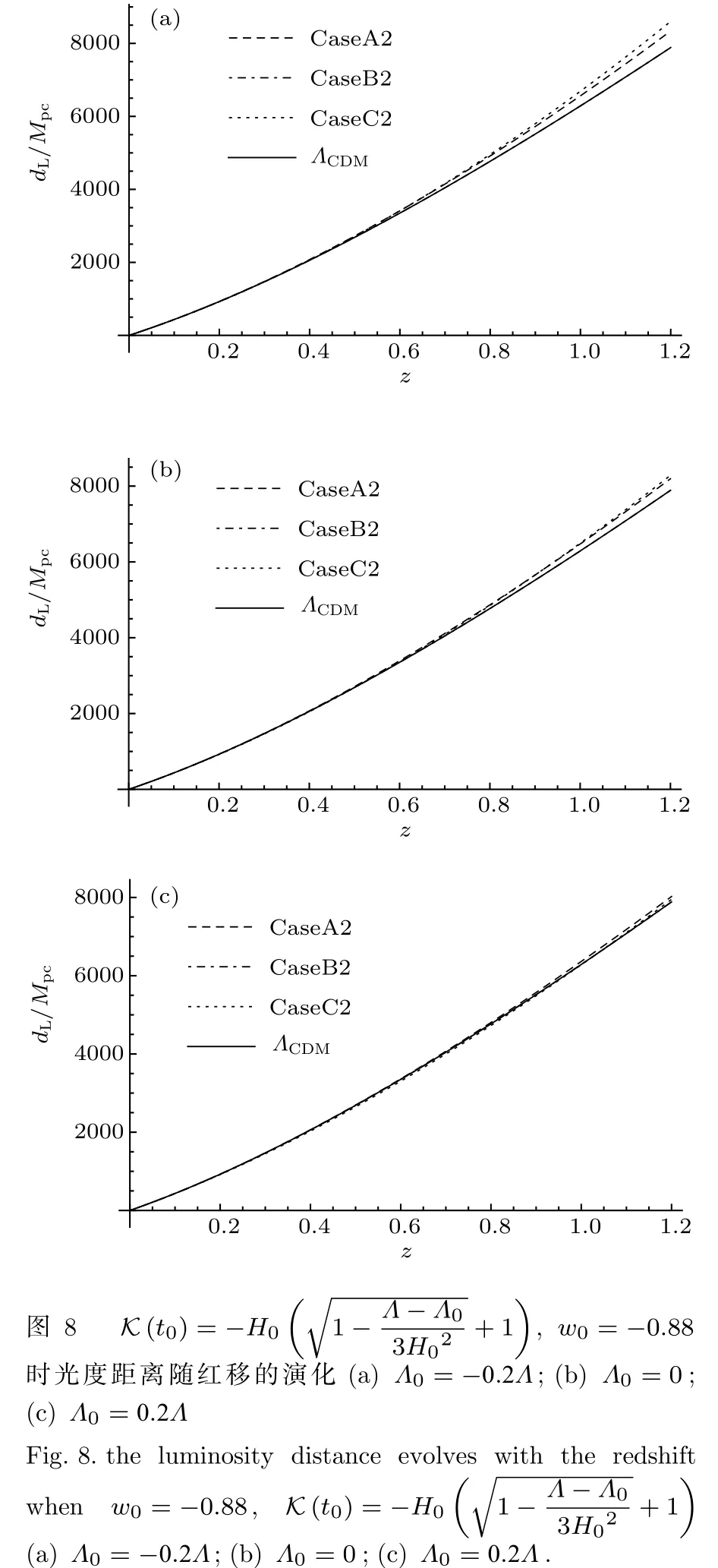
圖7和圖8給出了不同初值下光度距離隨紅移的演化結果.在長期的演化中,CaseB1和ΛCDM模型的結果趨近于完全相同,相較于CaseB1的演化結果,CaseA1和CaseC1與ΛCDM模型的演化結果對比差別要大些.并且CaseB2在長期的演化中也和ΛCDM模型的結果趨近于完全相同,但CaseA2,CaseC2的演化結果與ΛCDM模型相比要比差別要比CaseA1和CaseC1大.

4 計算結果與數據分析

圖9和圖10給出了距離模數的測量值與理論期望值的對比.比較(16a)和(18a)式發現ρΛ扮演了有效宇宙學常數的角色.由此我們可以定義表現為類標量場的有效勢能.對于所有的近似情況,可以求解Λ0臨界值的情況,它表示Λeff從單調下降的quintessence類型到有效宇宙學常數隨時間的演化出現局域極小類型轉變的臨界值.

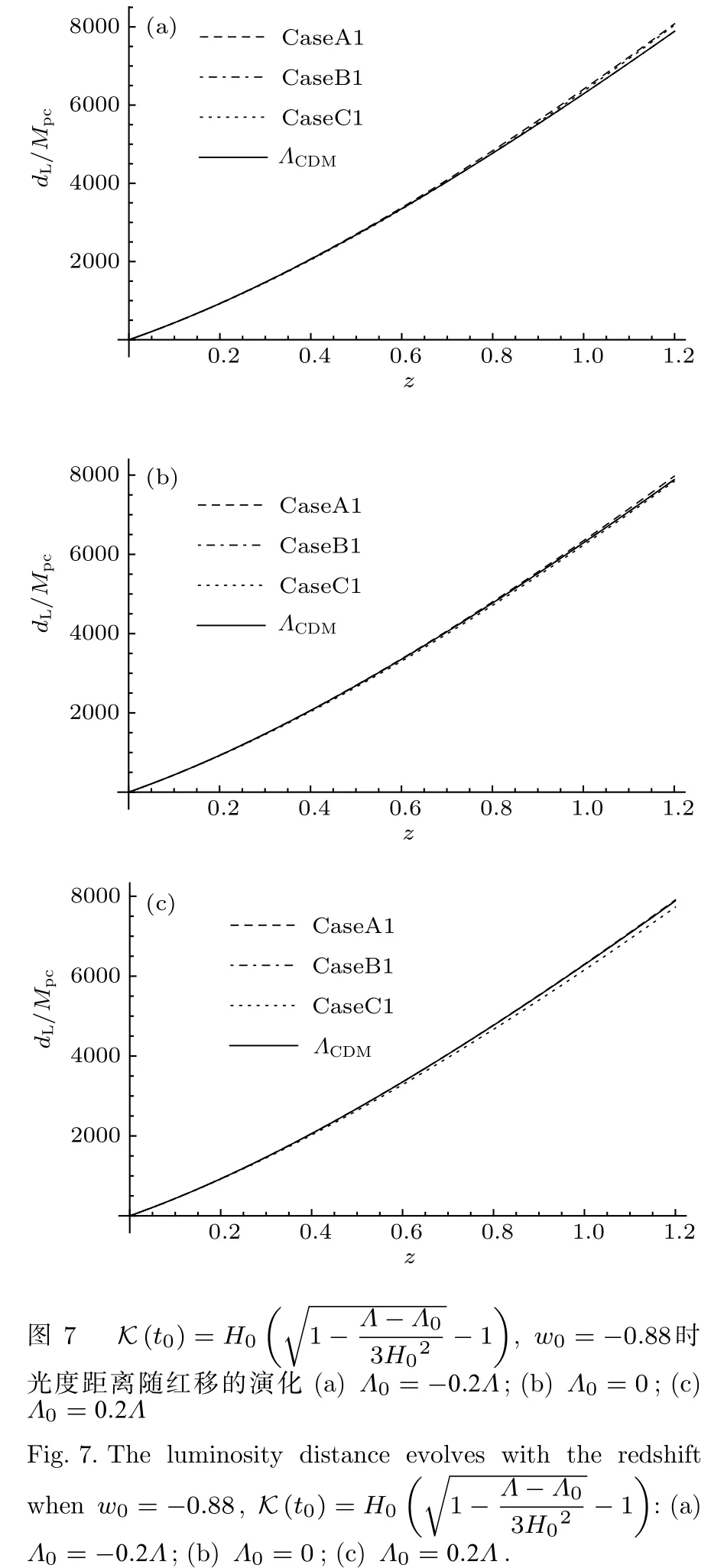
表2給出了不同模型下Λ0的臨界值情況,圖11和圖12將Λeff在臨界值附近隨時間的演化曲線清楚地表示了出來.對于CaseC,當時,對于所有Λ0,Λeff表現為單調下降的類quintessence勢,并且由圖9可知,通過天文觀測可以將時,Λ0大于0的情況排除.對于所有有臨界值的情況,Λ0?crit近似為0,我們可以推測Λ0?crit與0的偏差可能是由近似所引起的,在一個更詳細精準的模型中,它可能會有Λ0?crit=0.

對于弦景觀,有效的宇宙學常數Λeff表現為類quintessence類型的標量勢所驅動的演化,它滿足這兩個弦沼澤地判據.也就是說dS真空并不是宇宙加速膨脹所必需的,宇宙加速膨脹與量子引力是相容的.對于具有裸的正宇宙學常數的弦沼澤地,在最合理的近似下,有效宇宙學常數Λeff隨著時間的演化會出現局域極小,如果有標量場的勢能驅動其演化的話,必然不是quintessence類型.

5 總結與展望

實際上,從上文的分析可以看出,CaseC并不是一個很好的近似,原因可能是在暗能量部分的狀態方程中使用固定的w0.根據光度距離觀測值與理論期望值的比較,以及對Λ0臨界值在不同模型下的分析,可以得出結論: 從弦景觀中能夠產生有效的類quintessence勢,我們推測從單調下降的quintessence勢能類型到有效宇宙學常數(或者說類標量場的有效勢能)隨時間的演化出現局域極小類型轉變的臨界值Λ0為零.在我們的討論中事實上沒有涉及標量場,也沒有涉及標量場的勢能,我們給出的是有效宇宙學常數隨時間的演化.如果將這個有效宇宙學常數用一個標量場的真空勢能來等效地實現,這個標量場應該具有quintessence的行為,后續的研究將給出一個由quintessence勢能驅動的加速膨脹宇宙,其標量勢隨時間的演化與我們在這里的有效宇宙學常數預言之間的比較.

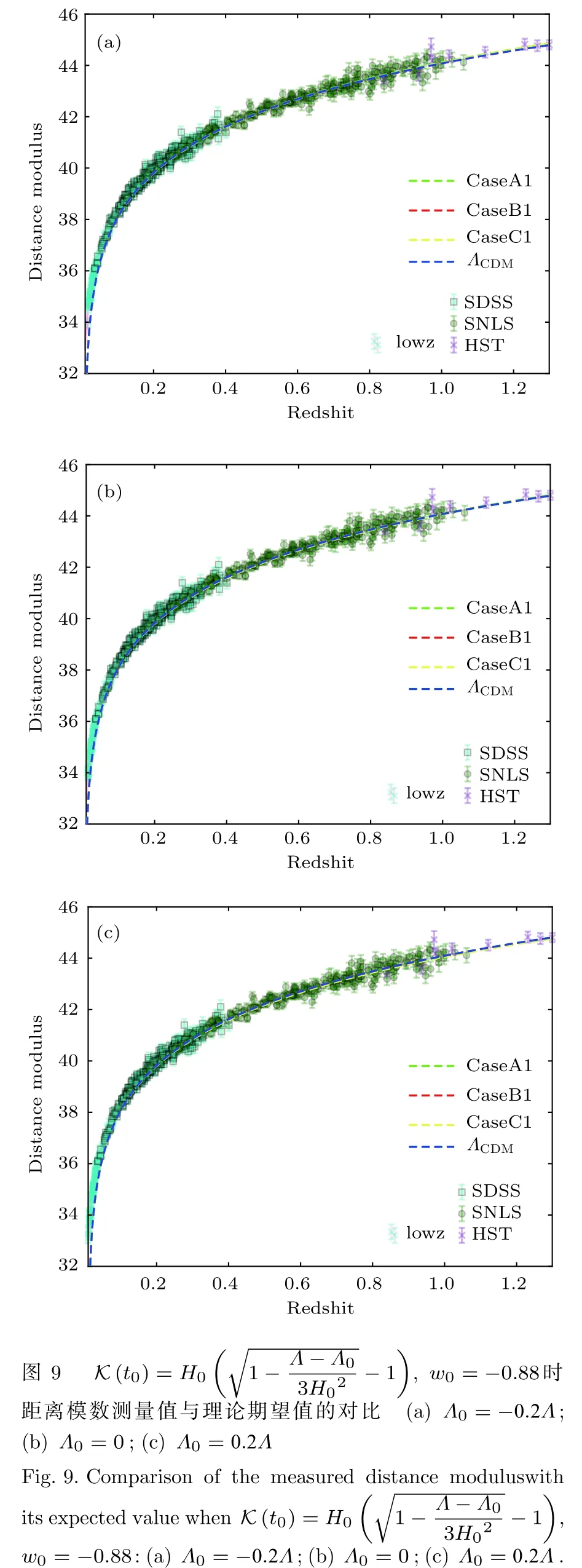
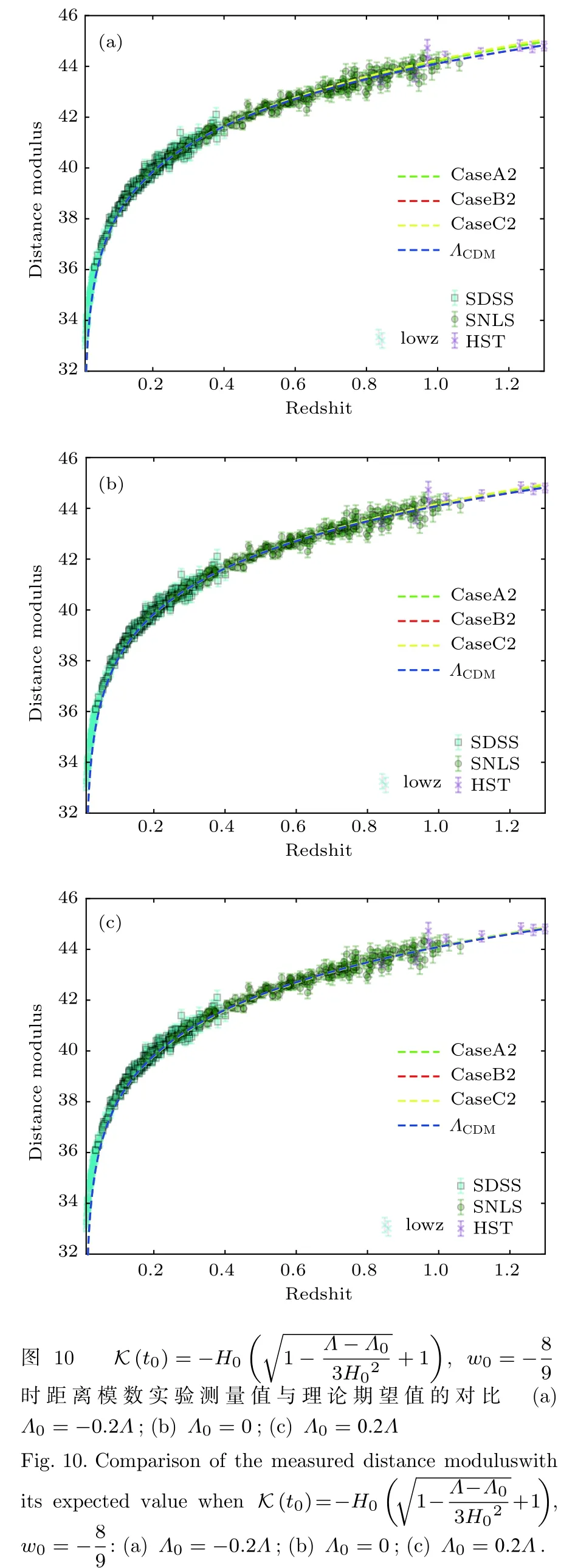
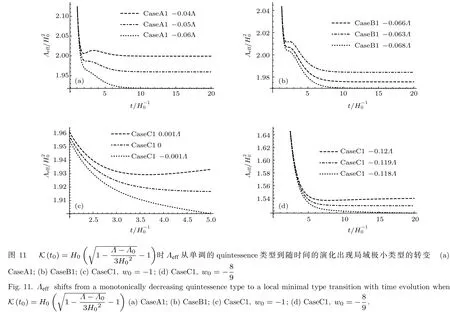
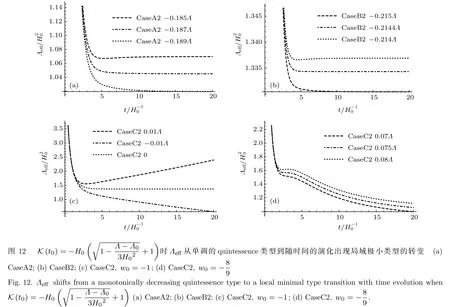
表2 在不同模型下有無 Λ0 的臨界值Table 2.Whether there are critical values of Λ0 under different models.