環狀聚合物及其對應的線性鏈熔體在啟動剪切場下流變特性的分子動力學模擬研究*

楊俊升 黃多輝

1)(中國科學技術大學,國家同步輻射實驗室,合肥 230026)

2)(宜賓學院,計算物理四川省高等學校重點實驗室,宜賓 644007)

1 引 言

環狀聚合物是自然界比較常見的分子形態,如質粒、基因組、肌動蛋白和多糖等分子結構[1?3].關于環狀聚合物體系的研究一直以來也是高分子物理研究中的熱點和難點之一[4?7].主要原因是環狀分子鏈與其相同分子量的線性鏈比較沒有鏈端,進而在其加工和實驗研究中就會表現出不同的應力響應和流變特性[8?10].目前實驗對于這一特殊的過沖響應的分子機理還沒有做出更清晰的分子機理解釋,實驗上也很難從分子層面觀察鏈段的演化信息,所以急需在分子層面對于這一應力過沖現象給出一個定性和定量的解釋.

目前,關于非串聯的環狀聚合物熔體的研究主要集中在其構象演變和流變性質.關于環狀聚合物構象的動力學研究,有些人認為環狀鏈是一個雙折疊的線性鏈[5],另一種觀點認為環狀聚合物在熔體中是網狀折疊分布的[11,12],而且應力是通過環與環之間的輪廓滑移松弛的.模型不一樣,所帶來的對應力松弛的解釋也就不同,目前這個問題仍然沒有得到解決.關于非串聯的環狀鏈熔體的流變學方面: 實驗結果顯示環狀鏈熔體的零剪切黏度明顯要比其線性鏈對應的黏度小,而且環狀聚合物熔體系對應的最大過沖應變與剪切速率之間并不滿足其線性鏈在高剪切速率下的1/3冪指數的標度關系,而且其對應的線性前驅體在剪切流場下具有明顯的應變過沖現象.最近的實驗研究還發現環狀分子熔體在剪切場下表現出了更弱的剪切變稀行為[8,9,13,14].故而,環狀聚合物結構和流變學研究中表現出來的差異性表明針對環狀聚合物熔體還需深入進行分子機理的研究.

目前關于環狀分子體系的研究,實驗很難測得高分子加工過程中分子鏈段的信息變化.分子動力學(moleculardynamics,MD)和非平衡分子動力學(non-equilibrium molecular dynamics,NEMD)模擬由于其精確的原子模型和小的時間尺度跟蹤能力,可以作為解決上述拉伸和剪切流變實驗問題的有效工具[15,16],從而為環狀聚合物熔體在不同流場強度下的分子過程提供有價值的分子圖像和理論解釋.本文主要以環狀聚合物及其對應的線性鏈模型體系為研究對象,通過非平衡分子動力學模擬方法探索其在剪切流場下所對應的結構和流變特性.

本文通過非平衡分子動力學方法對線性鏈和環狀聚合物體系在不同剪切流場下應力響應的分子機理做了系統的研究.雖然理想情況下需要一個全原子化的模型,但理解纏結聚合物熔體的宏觀動力學所需的體系的大小也是相當具有挑戰性的一個問題,特別是考慮到聚合物運動的時間和長度尺度時.因此,本文采用粗粒化模型(coarse-grained,CG)方法來獲取環狀鏈體系應力過沖對應的鏈拉伸和取向分子信息.動力學模擬結果不僅僅是再現了實驗觀察到的環狀鏈體系的流變特性,通過分子層面的觀察與分析,給出了環狀聚合物在不同剪切流場強度下應力響應所對應的分子結構與取向分子機理.

2 計算方法與模型

2.1 計算方法

本文采用分子動力學方法對纏結的聚合物熔體進行模擬,模擬軟件和平臺主要是在宜賓學院計算物理實驗室自行搭建集群上搭建的LAMMPS平臺上進行的.對于所研究的體系,粒子之間的非鍵相互作用采用Lennard-Jones(LJ)勢來描述[16]:

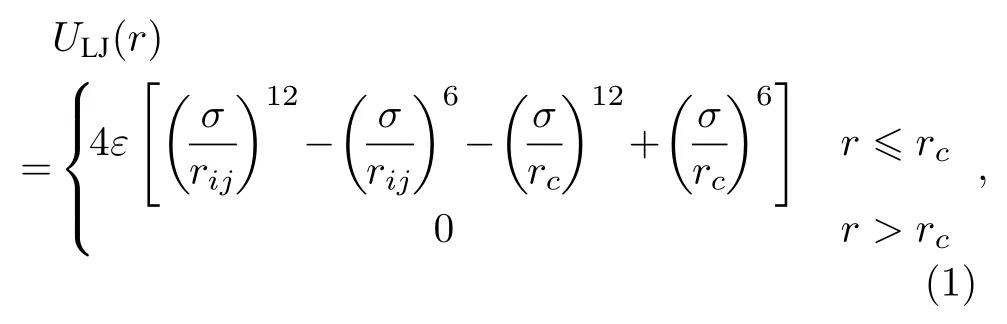
其中,rij為第i個珠子到第j個粒子或單體之間的距離,s是粒子或單體半徑.兩個粒子相互作用的截止距離為21/6s,對應于粒子之間的純斥力.在當前聚合物流變學研究中,吸引相互作用不應發揮重要作用,在此不予考慮.粒子之間的鍵合勢采用有限伸展非線性彈簧模型(FENE)來描述:

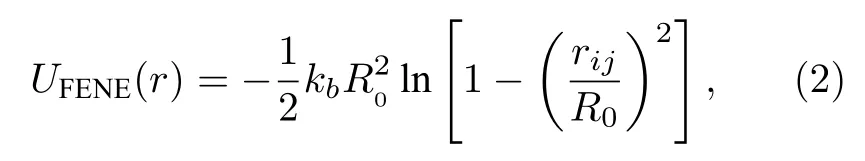
其中,彈性常數是kb=30ε/σ2,最大鍵長為R0=1.5σ.選擇較大的彈簧常數值,以減小網絡變形時鍵的拉伸效應.在模擬中,鏈上兩個珠子之間的實際平均鍵長是0.97s.

在MD模擬中,壓力張量P也稱為應力張量σαβ,或者僅僅是壓力.對角線單元稱為拉應力,非對角線單元稱為剪應力.因為壓強P是一個熱力學量應力,σαβ是一個力學量,前者定義為時間平均值,后者可即時計算.它們都是張量,滿足下面的關系:

在微觀系統中,壓力是根據維里方程作用在所有原子上的力之和計算出來的.對于加力場,這個方程通常寫成:

其中,N為計算域中存在的珠數,kB為玻爾茲曼常數,V和T為計算域中的體積和溫度,fij為珠i和j之間的力.

2.2 模型構建

為了研究線性鏈與它所對應的首尾相接的環狀鏈體系所的流變特性,本文構建了長度N=400的粗粒化線性鏈和環狀鏈分子體系,體系中包含了100根鏈,如圖1所示.為了比較方便,在數據分析過程中將它們分別標記為linear和ring.環狀鏈結構在熔體中非鏈接或者非串聯的.根據Likhtman 和Larson[17]的工作,知道分子鏈結構體系對應的纏結長度為Ne=50,并且計算出線性鏈和環狀鏈對應的松弛時間分別為1.45 × 105t和0.38 × 105t.初始結構建完之后,體系分別在T=1.0下松弛1 × 106t.兩種體系的初始密度都為0.85σ?3.當體系經歷了充分的松弛之后,再給體系施加剪切流場來計算其對應的流變特性.

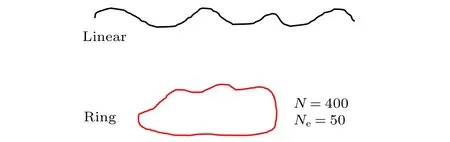
圖1 線性鏈與其對應的環狀鏈對應的結構Fig.1.The structure of linear and ring chains.

3 計算結果與討論

3.1 線性鏈及其環狀鏈熔體在不同流場強度下的應力及黏性響應

圖2(a)和圖2(c)示出了線性鏈與其同分子量的環狀鏈體系對應在不同流場強度下的應力-應變曲線.對于線性鏈,隨著應變的增加,剪切應力演化在各個應變速率下都存在一個過沖應變點,而且隨著剪切速率的增加過沖應變也在不斷地增加.應力過沖和軟化之后,線性鏈熔體對應的應力響應會進入一個平臺區,也就是穩態.但與其對應的環狀鏈體系比較,會發現當應變速率小于1 × 10–4t–1時,剪切應力沒有出現明顯的過沖現象,應力屈服之后直接進入的是一個平臺區.當剪切速率大于1 × 10–4t–1時,才出現了微弱的過沖現象.大應變速率下的應力響應與線性鏈的響應一致.繼續分析線性鏈和環狀鏈最大應力的大小,不難發現線性鏈最大應力比其環狀鏈對應的最大應力大很多.本文模擬結果與實驗所觀察到的結果也是一致的[8],證明我們選取的模型及模擬過程的合理性.同時,這個差異性也引起了我們的關注,但是實驗上關于這種現象的分子機理很難檢測到,也沒有給出明確的分子解釋.所以,很有必要在分子層面研究線性鏈與其對應的環狀鏈在不同剪切應變速率下的分子鏈段的拉伸和取向.黏性和剪切應力滿足以下公式[18,19]:

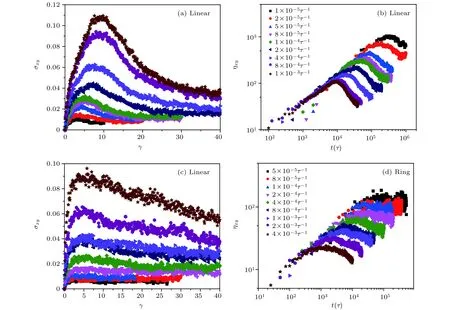
圖2 (a),(b)線性鏈體系對應的應力隨著應變及剪切黏性隨著時間的演化過程；(c),(d)環狀鏈體系對應的應力隨著應變及剪切黏性隨著時間的演化過程Fig.2.(a),(b)Stress-strain and nonlinear startup shear viscosity as function of strain and time for linear polymers,respectively;(c),(d)stress-strain and nonlinear startup shear viscosity as function of strain and time for ring polymers,respectively.

其中,σxy是剪切應力,是剪切速率.根據剪切應力和黏性的關系,圖2(b)和圖2(d)給出了線性鏈和環狀鏈的黏性隨著時間的演化過程.穩態峰值后的瞬時黏度降低反映了鏈的收縮(表現為部分解纏結或翻滾).隨著剪切速率越小,在穩態時對應的黏性越大；隨著剪切速率增大,黏性也會隨著減小,表現出了剪切變稀行為.

3.2 線性鏈及其環狀鏈熔體在不同流場強度下的流變特性

為了進一步給出線性和環狀鏈體系的流變特性的差異,從圖2中分別提取了線性和環狀體系在過沖點和穩態所對應的流變特性隨著流場強度的變化.為了分析和比較方便,這里將流場的強度轉換成維森伯格數(WiR=R),其中τR是線性鏈和環狀鏈對應的Rouse松弛時間.線性鏈的松弛時間是其對應的環狀鏈松弛時間的4倍(τR.ring=τR.linear/4)[8,20].根據Likhtman 和Larson[17]的工作,可計算出線性鏈和環狀鏈對應的松弛時間分別為1.45 × 105t和0.38 × 105t.根據松弛時間τR和剪切速率,就能給出相應的剪切速率下其對應的維森伯格數WiR.

圖3(a)示出了穩態黏性隨著時間的變化.隨著WiR的增加,線性和環狀鏈體系都表現出了剪切變稀的行為,但是環狀鏈體系所表現出來的剪切變稀行為明顯要比線性鏈的更弱.線性鏈和環狀鏈體系所應的黏性變化與WiR之間所滿足的標度關系與實驗測量出來的標度關系也是吻合的,這也從側面證實我們構建的模型是合理的[8,13],可以進一步探索其流變特向所對應的結構變化.

圖3(b)示出了體系在剪切過程中最大黏性和穩態黏性的比值(ηmax/ηsteady)隨著WiR的變化,其反映的是穩態有效鏈的形變量.事實上,當WiR<1時,對于線性鏈和環狀鏈,ηmax/ηsteady都是趨近于1的,在這個區間鏈實際上有足夠的時間松弛.當WiR>1 時,隨著剪切速率的增加ηmax/ηsteady也隨著增加,并且線性鏈和環狀鏈體系與時間的剪切強度表現出了不同的標度關系,0.08明顯也要比線性鏈的0.13小.進一步證實了穩態流場下線性鏈的線團要比環狀鏈的線團容易發生形變.

圖3(c)示出了最大應力所對應的峰應變(γmax)隨著WiR的變化過程.對于線性鏈,應力過沖響應中所展現的標度關系在早期的流變學實驗中也有發現,而且這些標度關系目前也被其他理論模擬證實.當WiR<1 時,應力過沖主要是由于聚合物鏈段的取向過沖所引起的,而且最大過沖應變主要處于應變為1.8—2.3之間[8,14,21,22].當WiR>1 時,應力過沖主要是由聚合物鏈段的取向和拉伸的協同作用決定的,而且γmax與WiR之間滿足指數為1/3的標度關系.對于環狀鏈體系,分析結果顯示γmax與WiR之間滿足指數為0.1,也明顯小于其線性鏈對應的標度指數.圖3(d)給出了線性和環狀鏈體系所對應的最大應力σmax與WiR之間的關系,我們發現相同的WiR下最大應力與體系的構象沒有關系,隨著剪切速率增加線性鏈和環狀鏈體系都滿足指數為0.5的標度關系.

從流變特性的變化,可以認為雙折環的構象是其變形能力較弱的主要原因.換言之,與其對應的線性鏈相比,環型聚合物由于結構緊湊,在剪切流作用下改變構象的自由度較小.此外,環狀鏈的鏈段在剪切流作用下的協同運動與線性鏈段的運動不同.這是都是實驗所無法觀察到的,需要通過分子模擬進一步驗證.

3.3 穩態線性及其環狀分子整鏈構象與取向在不同流場強度下的演化

為了進一步探索線性鏈及其對應的環狀鏈達到穩態以后的分子構象和取向的變化,本文計算了回轉半徑(Rg)和取向角(tan2q)的隨著流場強度的變化,如圖4所示分別表示整鏈的均方回轉半徑和初始結構的均方回轉半徑)代表分子鏈的形變程度.從圖4(a)中不難發現,小WiR下線性鏈體系更容易形變,但是當WiR>20時,在相同的WiR下,兩者的形變也基本相同,并且都滿足的冪指數關系.

圖4(b)給出了線性鏈和環狀鏈體系與流場方向取向角的變化.環狀分子和線性分子的取向采用以下的方程來描述[13]:

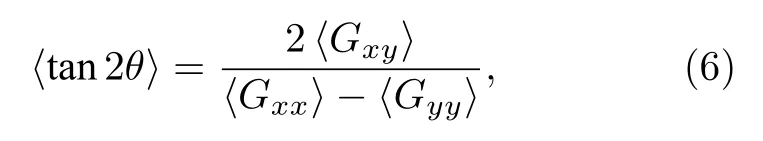
其中,Gxy,Gxx和Gxy分別代表分子鏈構象在不同方向上的回轉張量平方.從圖4(b)中可以看到線性鏈和環狀鏈的取向隨著WiR的增加而減小,但是線性鏈明顯要比環狀分子更容易發生取向,并且線性鏈和環狀鏈的平均取向角與流場強度WiR分別滿足的標度關系.

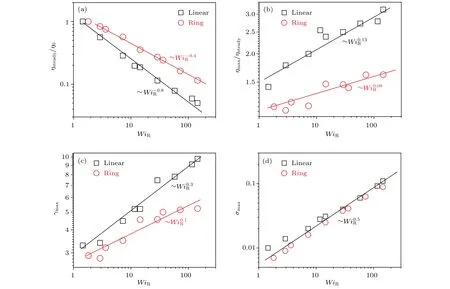
圖3 不同流場強度下線性鏈及其環狀鏈的歸一化穩態黏性 ηsteady/η0(a),最大黏性和穩態黏性比值 ηmax/ηsteady(b),峰應變γmax(c)和最大應力 σmax(d)隨著 WiR 的變化Fig.3.(a)Evolution of steady viscosity normalized with the zero-shear viscosity ηsteady/η0 ,(b)maximum viscosity scaled with steady viscosity ηmax/ηsteady ,(c)peak strains γmax and(d)peak shear stress σmax as a function of WiR.

3.4 線性及其環狀分子鏈段構象和取向分布的演化過程

為了進一步探究不同剪切流場下,環狀鏈與其對應的線性鏈分子鏈段信息的變化,將線性和環狀分子按纏結長度Ne=50分成小段來考察鏈段的分布和拉伸比分別對應的是開始剪切之前鏈段的平均末端距和不同應變下鏈段的平均末端距)及鏈段沿著流場方向取向角分布及平均值鏈段矢量與流場方向的平均夾角)的變化.

圖5示出了不同WiR下鏈段的長度分布概率及鏈段平均拉伸比隨著應變的變化過程.在弱流場下,線性鏈與其環狀鏈對應的鏈段的分布基本上是高斯分布,平均拉伸比保持在1附近.但是當WiR增加到10以后,會發現線性鏈的鏈段的平均拉伸比會明顯增加,而且到達最大值后會有一個明顯的拉伸過沖現象,暗含鏈段有一個明顯的回彈.相比于線性鏈,環狀鏈體系的鏈段拉伸比在強流場下沒有出現明顯的過沖現象,這與目前看到的應力沒有明顯的過沖現象也是一致的,從而可以推斷環狀鏈體系之所以沒有明顯的過沖現象是由于環狀鏈自身弱的拉伸比及剪切過程中鏈段沒有明顯的回彈導致的.最近Kremer等[1]的結論也證實了環狀高分子鏈在小應變速率下構象不發生明顯的拉伸,從側面也驗證了我們的結論[6].不僅僅是環狀高分子鏈分子存在這樣的現象,環狀的DNA分子與其線性鏈比較的實驗也發現了類似的結果.圖6給出了鏈段取向角的分布變化.對于線性鏈和環狀分子,在低剪切速率下,鏈段的取向都沒有發生明顯的變化,而且θ分布都很寬,但是隨著流場強度的增加,θ的分布也明顯變窄,表明分子鏈段存在明顯的取向.當體系達到穩態之后,線性鏈體系和環狀分子體系θ并沒有減小.從而可以推斷: 線性鏈體系表現出明顯的過沖主要是由于鏈段的拉伸回彈導致的.環狀鏈體系之所以沒有表現出明顯的過沖現象是由于其分子的鏈段到達穩態之后并沒有出現明顯的回彈.

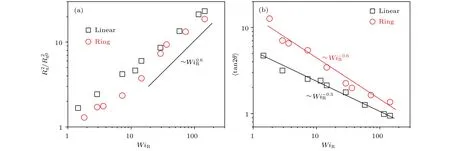
圖4 (a)線性鏈和環狀鏈體系的 ＜＞/＜＞ 隨著 WiR 的變化；(b)線性鏈和環狀鏈熔體的取向 ＜tan2θ＞ 隨著 WiR 的變化Fig.4.The ＜＞/＜＞(a)and tan2θ(b)as a function of WiR for linear and ring polymers.

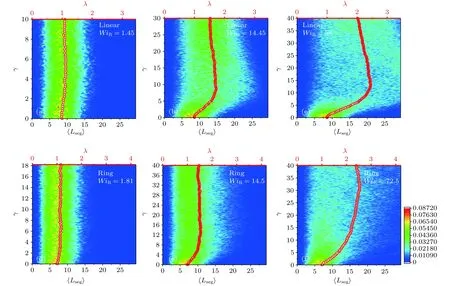
圖5 不同 WiR 下線性與環狀分子鏈段長度分布隨著應變的演化Fig.5.Evolution of segmental length distribution of linear and ring polymers under the different WiR.

4 結 論

本文通過非平衡分子動力學方法研究了環狀分子及其對應的線性鏈分子體系在啟動剪切流場下的結構和流變特性.動力力學模擬結果顯示: 線性鏈與其對應的環狀分子比較在低維森伯格數下具有更明顯的應變過沖現象.這主要是由于線性分子鏈段在剪切場下發生了明顯的回彈、但是環狀鏈體系并沒有出現明顯的回彈所引起的.本文還提取了線性鏈和環狀鏈體系在過沖點和穩態的流變數據(黏性、過沖應變、過沖應力及最大黏性與穩態黏性的比值),并給出了線性鏈和環狀鏈體系流變特性分別滿足的標度關系,為進一步的實驗研究提供了理論參考.

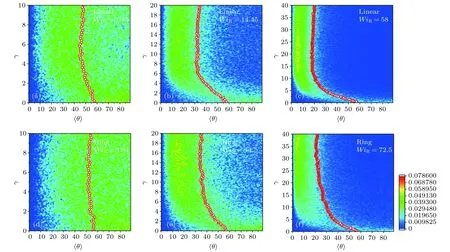
圖6 不同 WiR 下線性與環狀分子鏈段沿著剪切方向角分布隨著應變的演化Fig.6.Evolution of segmental angle distribution for linear and ring polymers under the different WiR.