平面P波入射半無限介質內運動空間特征研究

何衛平, 周宜紅

(1.三峽大學 湖北省水電工程施工與管理重點實驗室，湖北 宜昌 443002;2.三峽大學 水利與環境學院，湖北 宜昌 443002)

受到地質地形條件影響，地震波在場址引起的地震動具有空間差異性[1]。研究顯示，地震動的空間差異不僅影響結構地震響應規律，也可能帶來結構地震響應的顯著增加[2-5]。橋梁、核電站和大壩等大跨度結構的地震安全性評價體系中，獲得能合理描述地震動空間差異的輸入模型是亟待解決的問題。

已有研究顯示，引起地震動空間差異的原因主要有行波效應、衰減效應、相干效應和局部場地效應等因素。目前工程應用領域通常采用相干函數模型描述地震動的空間差異[6]，已有相干函數模型主要可區分為通過實測臺陣記錄總結得到的經驗模型[7-8]，和結合實測臺陣記錄與理論分析的半經驗模型[9-10]。相干函數為描述地震動空間相關性提供了合理的途徑，已提出的諸多相干函數模型可為工程結構的非一致地震響應分析提供應用基礎。然而，大壩、核電站的地震響應分析通常不僅關注地面運動，還關注地基內一定深度的地震動[11-12]。另外，相干函數屬唯象模型，側重地震動空間差異的經驗性描述，沒有從物理過程考察地震動場的特征[13]，在解釋地震動空間差異的形成機理方面略顯不足。現階段，研究地震動空間差異的形成機理，是解決空間差異地震動輸入模型的關鍵環節。

空間差異地震動是入射地震波在場址條件下形成的運動，從形成機理出發研究地震動場，必須從入射波形成場址運動場出發。在地震波引起的空間運動研究方面，目前在波動輸入模型方面有所涉及。如劉晶波等[14-15]在發展黏彈性邊界波動輸入模型時對側邊界運動的處理，考慮了入射波與反射波的疊加影響。但波動輸入模型側重于輸入相關運動，在解釋地震動空間差異方面關注較少。另外，在工程應用領域，以描述地震動空間差異為目標的模型有金星等[16]提出的地震動隨機場模型和張翠然等[17]提出的隨機有限斷層法模型。這兩類模型均以隨機方法為基礎，通過模擬地震波從震源到場址的傳播過程構建地震動場。

本文嘗試從波動理論及疊加原理出發研究場址小范圍內的確定性地震動空間差異，討論范圍除地面質點運動外，也包含地基內質點的運動。文中首先以半無限介質內入射P波與SV波疊加形成的質點運動為例，對地震波疊加模式與質點運動空間差異進行說明。然后以P波垂直入射為例，對疊加區和分離區、分界線等概念進行界定，并對由地震波疊加模式不同引起的運動空間差異進行說明。最后針對平面P波傾斜入射情況研究空間域劃分，并通過算例研究疊加區內質點運動的空間特征。

1 地震波疊加模式與質點運動空間差異

地震波在介質內的傳播引起質點運動，如平面P波引起的質點運動與傳播方向平行，平面S波引起的質點運動與傳播方向垂直。當多條地震波在相同空間區域傳播時，質點運動由地震波運動疊加形成。由于空間域內的地震波可能存在波型、持時、傳播方向、初至時間等的差異，不同空間位置質點的運動疊加方式存在差異。

以圖1波在無限均勻介質中的傳播為例，假設無限介質內存在平面P波和SV波，兩條地震波持時均為2 s，位移峰值1 cm，入射角分別為40°和35°，波形如圖所示，兩條地震波到達A點的時間相同。依據疊加原理，可由P波與SV波的波函數獲得空間內任意質點的運動時程。以地震波傳播到達A點為零時刻，在圖中顯示了A、B、C三個空間點的水平向運動時程。

分析地震波傳播特點和質點運動時程，圖示A、B、C三個位置的地震波疊加模式存在如下差異。在A點，P波與SV波在相同時刻到達、相同時刻離開，A點運動的整個時段均由兩條地震波疊加形成。在B點，P波先于SV波到達且更早離開，運動的前段由P波形成、中段由P波和SV波疊加形成，后段由SV波形成。在C點，P波首先到達并通過，此后SV波到達并通過，質點運動前段由P波形成，后段由SV波形成。地震波疊加模式的差異帶來質點運動的差異，下面以質點運動的水平分量為例，分別從持時、峰值和時程形狀三方面分析。

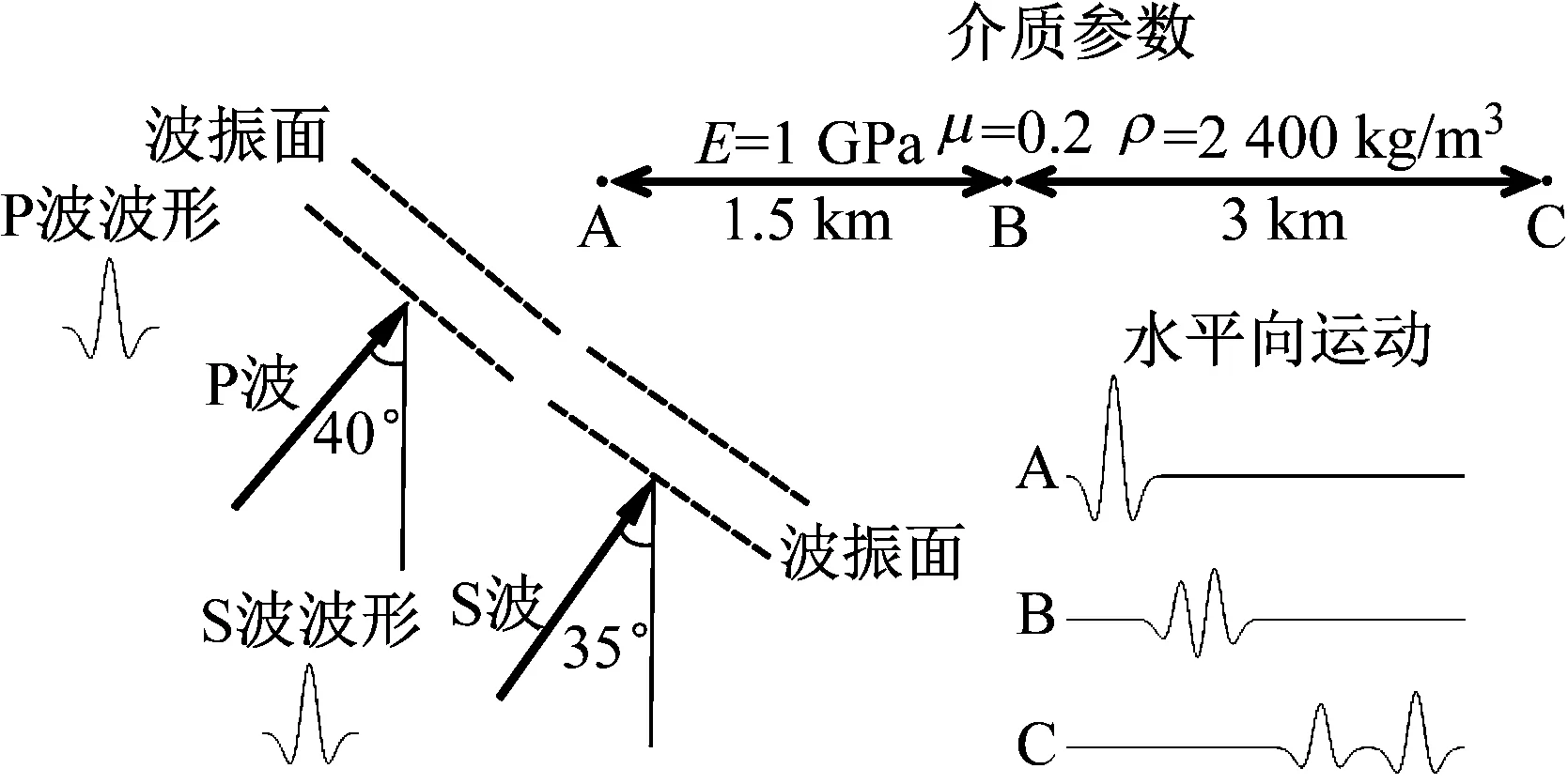
圖1 地震波疊加模式與質點運動空間特征示意圖

Fig.1 Superposition mode of waves and spatial variation of particle motion

在持時方面，A點運動整個時段均由P波和SV波疊加形成，持時為2.00 s；B點存在P波和SV波單獨形成時段和疊加形成時段，持時為2.65 s；C點運動不存在兩條地震波的疊加形成時段，持時為4.00 s。

在運動峰值方面，A點運動由兩條地震波直接疊加形成，峰值為1.46 cm；B點運動存在兩條地震波疊加貢獻時段，負峰值與正峰值存在疊加影響，峰值為0.75 cm；C點運動中兩條地震波的貢獻時段在時域分離，峰值為0.82 cm。

在質點運動時程形狀方面，從圖1可知由于地震波疊加模式差異質點的運動形狀存在明顯的不同。

綜上，介質內部地震波的傳播效應和疊加模式差異會引起質點運動的空間差異，研究組合地震波對質點運動空間差異的影響，對地震動空間差異的形成機理研究具有重要意義。

2 P波垂直入射空間域劃分

為對問題有較清晰的認識，首先選取較為簡單的平面P波垂直入射工況，研究在入射波和反射波影響下質點運動疊加模式差異和空間域劃分情況。

2.1 平面P波垂直入射

圖2顯示半無限均勻介質內平面P波垂直入射情況，圖中空心箭頭代表地震波傳播方向，實箭頭代表質點振動正方向。依據自由面處應力和位移邊界條件，可得反射P波的幅值系數APR=-1。P波垂直入射時，半無限空間內存在入射P波(簡寫為PI)和反射P波(簡寫為PR)兩條地震波，空間內質點運動是兩條地震波運動的疊加。

2.2 空間域劃分

以圖2中質點A(x,z)為研究對象，質點運動由入射P波和反射P波運動疊加形成。由于入射波和反射波均具有固定持時，且地震波在介質中傳播需要時間，兩條地震波的疊加模式隨A點位置而變化。

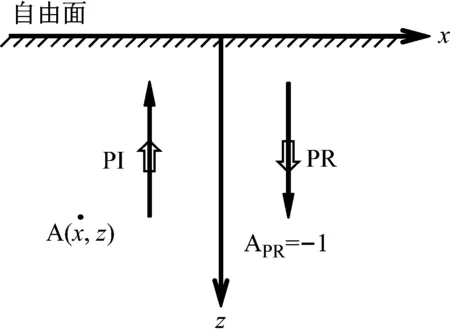
圖2 平面P波垂直入射示意

A點位于自由面時，由于入射波到達自由面時立即產生反射波，兩條地震波在質點運動的整個時段均有貢獻，即質點運動是由兩條地震波全時域疊加形成。

A點與自由面距離為z時，入射波首先到達，此后經過距離z傳播到自由面并形成反射波，反射波經過距離z傳播到質點。此時可依據質點位置將疊加模式分為兩種情況：當質點距離自由面較近時，入射波與反射波在質點的運動時程中存在疊加貢獻時段，將此類質點所在空間定義為疊加區；當質點距離自由面較遠時，入射波與反射波對質點運動時程的貢獻時段是分離的，將此類質點所在空間定義為分離區。自由面屬于疊加區。

由于P波垂直入射，因此疊加區與分離區的分界線應為與x軸平行的直線。在圖3中顯示了疊加區與分離區的示意圖，圖中質點運動為依據第3節算例獲得的區域內特征點豎直向運動時程。

圖3 質點運動疊加模式與空間區域

2.3 疊加區與分離區的分界線

以PIs和PIe分別代表入射P波到達和離開質點的時間，以PRs和PRe分別代表反射P波到達和離開質點的時間，T代表地震波持時。

以入射波到達自由面為時間零點，依據地震波速得到P波垂直入射時，入射波到達和離開空間點(x,z)的時間PIs和PIe分別表達為式(1)和式(2)，反射波到達和離開空間點(x,z)的時間PRs和PRe分別表達為式(3)和式(4)。式中z代表空間點的豎直坐標，vp代表P波傳播速度，波速表達式見式(8)。

PIs=-z/vp

(1)

PIe=-z/vp+T

(2)

PRs=z/vp

(3)

PRe=z/vp+T

(4)

當入射波離開時刻與反射波到達時刻相同，即PIe=PRs時質點運動時程中兩條波的貢獻時段在時域相接，該質點也位于分界線上。依據式(2)和(3)得到式(5)，該式代表P波垂直入射時疊加區與分離區的分界線。

zd=vpT/2

(5)

3 疊加區域運動空間差異

3.1 介質參數及入射地震波

選取彈性模量為10 GPa、泊松比0.2、密度2 400 kg/m3的半無限彈性介質為例進行研究。為表達清晰，選取入射地震波為Ricker子波，子波運動時程在圖4顯示，圖中位移正值代表與z軸正方向一致。

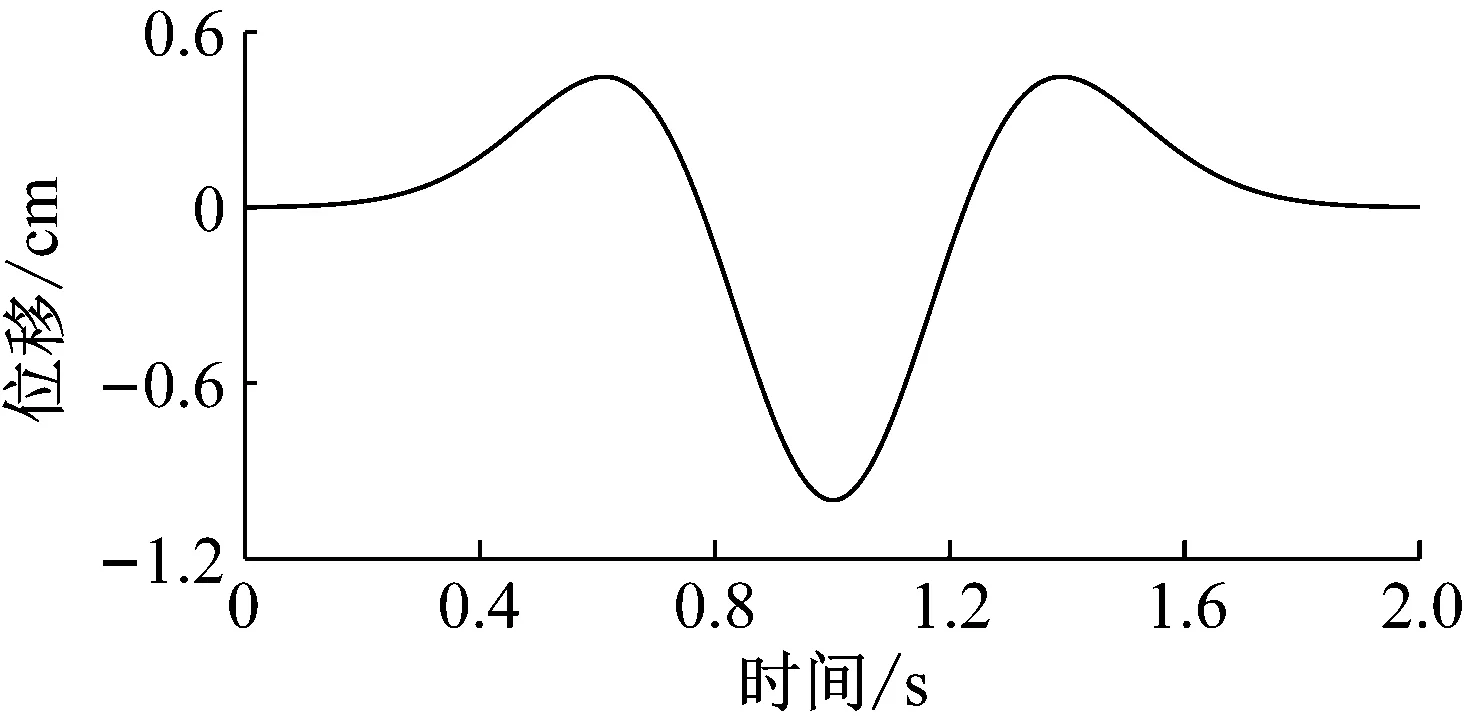
圖4 Ricker子波位移時程

3.2 疊加區質點運動空間差異

P波垂直入射時，入射波與反射波引起的運動與傳播方向平行，即質點運動表現為豎直向運動，因此本部分僅考察質點運動的豎向分量。依據入射波與反射波各自的波函數疊加，得到空間內任意點的運動時程。

依據介質參數和地震波持時，由式(5)得到分界線的深度為2.15 km。選取自由面和深度0.6 km的疊加區特征點研究。圖5顯示了兩個特征點的運動時程，圖中時間零點代表地震波到達該位置的時刻，斜體字及雙箭頭代表對質點運動時程產生貢獻的地震波及其貢獻時段。

在自由面上，入射波到達即產生反射波，入射波與反射波疊加形成質點運動。自由面質點運動持時與入射波持時相同，且質點運動峰值是入射波峰值的2倍。

在深度為0.6 km處，由于入射P波到達0.56 s之后反射P波到達，因此入射P波貢獻時段為0～2 s；反射P波貢獻時段為0.56～2.56 s。在0～0.56 s質點運動僅受入射P波影響，在0.56～2 s質點運動同時受到入射P波與反射P波影響，在2～2.56 s質點運動僅受反射P波影響。由于地震波傳播效應，0.6 km深度的質點運動持時增加了0.56 s；由于入射波和反射波的疊加影響，質點運動峰值由1.00 cm減小到0.78 cm。

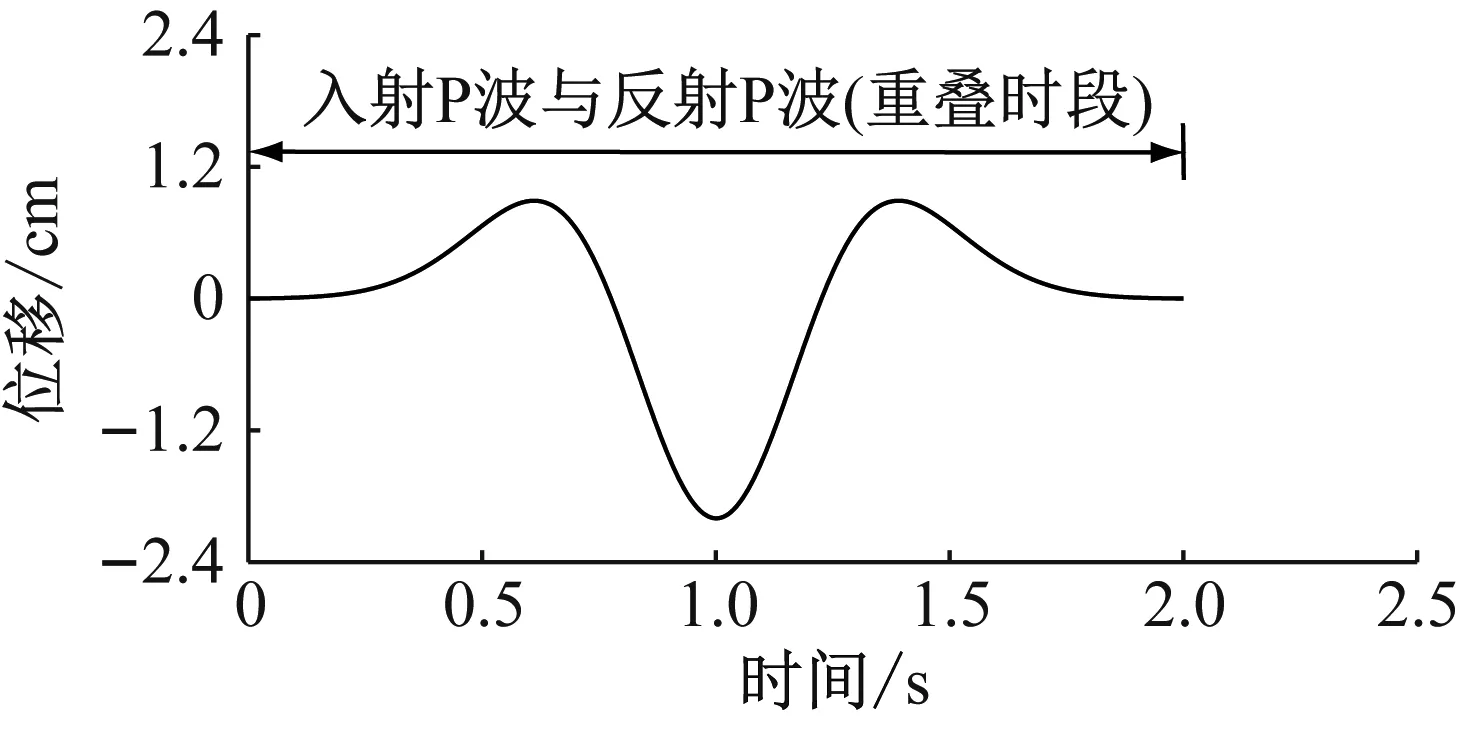
(a) 自由面

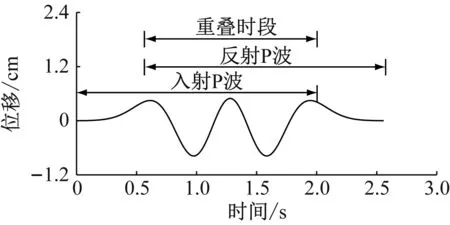
(b) 深度0.6 km

兩個質點運動對比可看出：由于所處位置不同，受到地震波傳播所帶來的疊加方式影響，不同質點運動時程在持時、峰值和時程形狀等方面均表現出較大空間差異。

圖6顯示了P波垂直入射時疊加區內質點運動位移峰值沿豎向分布。由于Ricker子波負峰值為單峰，對負峰值進行分析。位移負峰值主要顯示出以下規律：① 疊加區峰值出現較大變幅，從地表到約0.5 km深度，位移峰值從2 cm逐漸減小到0.55 cm；② 位移峰值在一定深度以下變化到與入射波位移峰值相等。位移正峰值在接近自由面呈現出與負峰值相同的規律，但由于選用的波形存在兩個正峰值，其疊加規律更為復雜，幅值變化的范圍也有明顯增大。

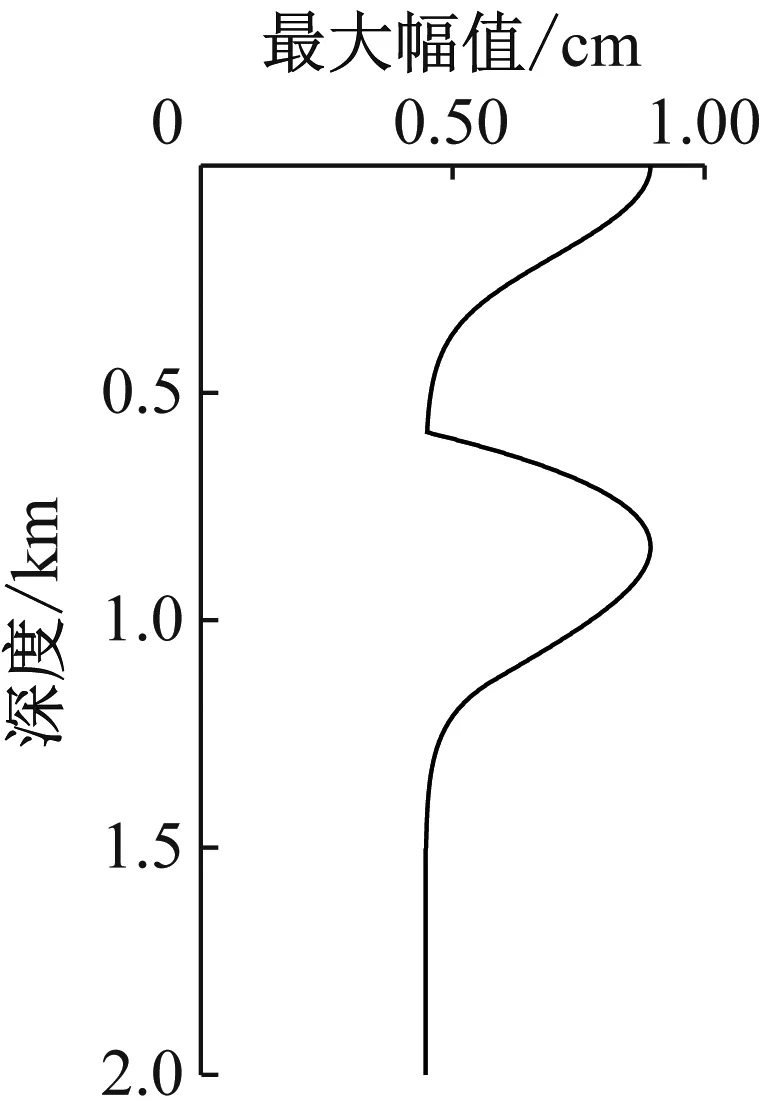
(a) 正峰值

(b) 負峰值

4 P波傾斜入射質點運動空間特征

4.1 傾斜入射反射系數

P波(記為PI)傾斜入射到自由面時，會產生反射P波和SV波(分別記為PR、SR)，如圖7所示。圖中符號含義與前文相同，θ為P波入射角，θ′為SV波反射角。反射P波、反射SV波幅值系數分別用Ap表示。依據自由面應力和位移邊界條件，可得出反射P波和SV波的幅值系數為式(6)和式(7)。波速vp、vs分別代表P波和SV波波速，E、μ和ρ分別代表半無限介質的彈性模量、泊松比和密度。

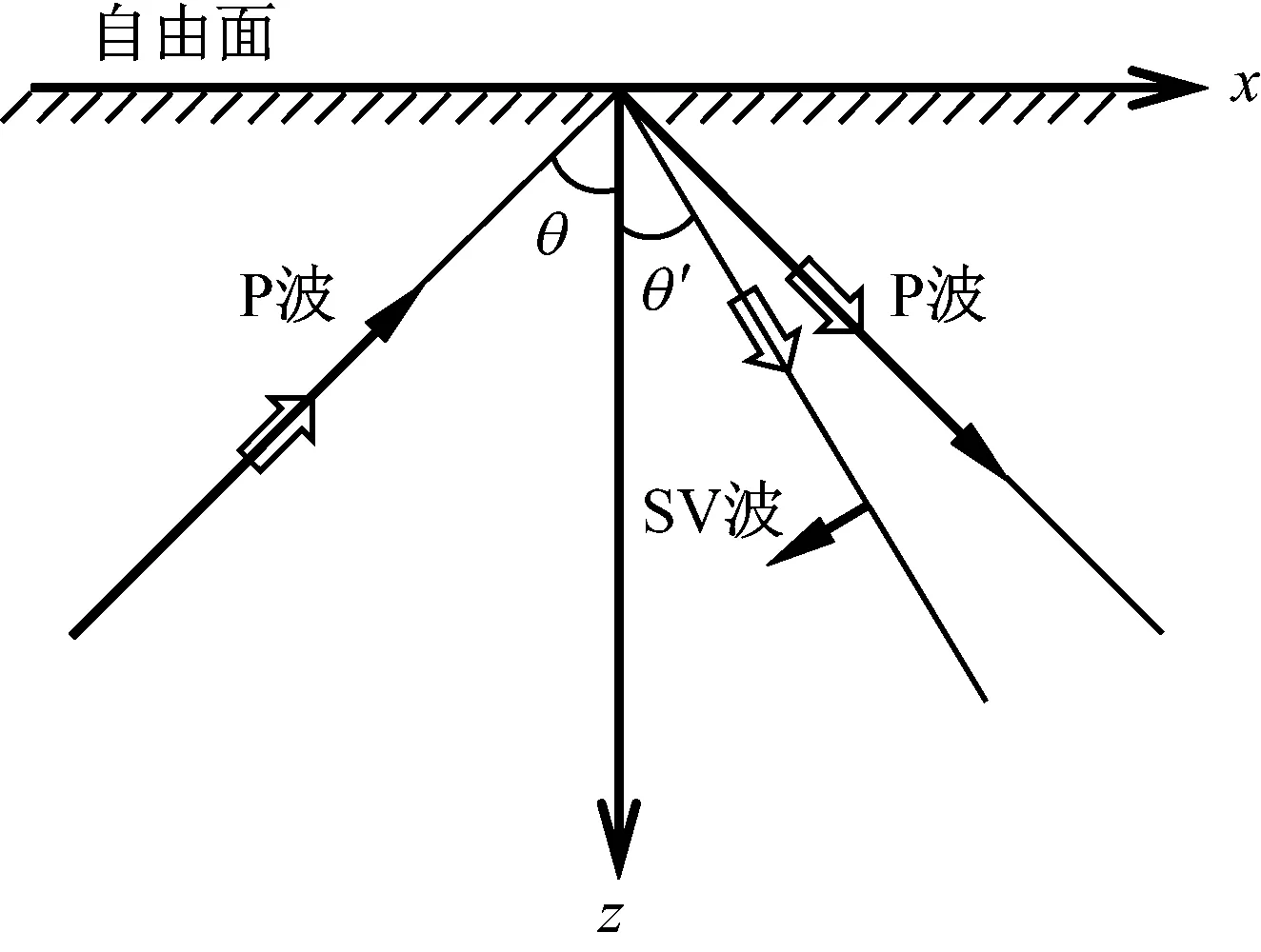
圖7 平面P波傾斜入射示意

(6)

(7)

(8)

(9)

4.2 空間特征區域

半無限介質中存在三條地震波，質點運動由三條地震波運動疊加形成。依據與第4節相同的分析方法，可得到在任意空間點(x,z)，入射P波的到達和離開時間PIs和PIe分別表示為式(10)和式(11)，反射P波的到達和離開時間PRs和PRe分別表示為式(12)和式(13)、反射SV波的到達和離開時間SRs和SRe分別表示為式(14)和式(15)。

PIs=(xsinθ-zcosθ)/vp

(10)

PIe=(xsinθ-zcosθ)/vp+T

(11)

PRs=(xsinθ+zcosθ)/vp

(12)

PRe=(xsinθ+zcosθ)/vp+T

(13)

SRs=(xsinθ′+zcosθ′)/vs

(14)

SRe=(xsinθ′+zcosθ′)/vs+T

(15)

由于涉及地震波之間的分離和空間區域的分界，將地震波之間的分離坐標稱為分離線，將空間區域的劃分坐標稱為分界線。依據以上公式，可得出PI與PR的分離線坐標為式(16)、PI與SR的分離線為式(17)、PR與SR的分離線坐標為式(18)。

z1=vpT/2cosθ

(16)

z2=vpvsT/(vpcosθ′+vscosθ)

(17)

z3=vpvsT/(vpcosθ′-vscosθ)

(18)

在三條地震波存在情況下，分離區應滿足三條地震波對質點運動時程無重疊貢獻時段，因此分界線應為三條分離線中的最大值。考慮到實際場址地震波通常為小角度入射，此時分界線為z3。通過z3表達式可知，當P波傾斜入射時分界線仍與x軸平行。

zd=z3=vpvsT/(vpcosθ′-vscosθ)

(19)

4.3 半無限空間質點運動表達式

圖7所示半無限介質內，入射P波的波函數可用式(20)表示，反射P波和反射SV波的波函數可分別用式(21)和式(22)表示。

(20)

(21)

(22)

疊加入射P波、反射P波和反射SV波的波函數，可得到半無限介質內任意空間點運動的水平分量和豎直分量分別為式(23)和式(24)。

h(t,x,z)=g(t,x,z)sinθ+

gp(t,x,z)sinθ-gs(t,x,z)cosθ′

(23)

v(t,x,z)=-g(t,x,z)cosθ+

gp(t,x,z)cosθ+gs(t,x,z)sinθ′

(24)

假設空間坐標由(x,z)變化為(x+Δx,z)，依據式(20)～式(24)和斯奈爾定律式(25)可得到式(26)和式(27)。

vp/vs=sinθ/sinθ′

(25)

(26)

(27)

公式(26)和(27)的物理意義為：在半無限介質內P波傾斜入射情況下，位置(x+Δx,z)處質點的運動，與(x,z)位置質點在Δxsinθ/vp時間后的運動相同。也可描述為質點運動的時程形狀不隨水平坐標變化。因此研究半無限介質P波傾斜入射情況質點運動空間特征時，可重點關注質點運動沿豎向的變化。相關公式中當θ=0時代表垂直入射情況，因此公式(26)和(27)對P波垂直入射和傾斜入射均適用。

4.4 疊加區運動空間差異

采用與第3節相同的介質參數，假設P波以30°傾斜入射，依據式(19)可得到分界線深度為6.25 km。分別選取自由面和深度2 km質點作為特征點。

圖8顯示了兩個特征點的水平向運動時程，圖中時間零點代表地震波傳播到達該位置的時刻。當P波以30°入射時，自由面質點運動中入射波和反射波貢獻時段都為0～2.00 s；深度2 km處質點運動時程中，入射P波貢獻時段為0～2.00 s，反射P波貢獻時段為1.61～3.61 s，反射SV波貢獻時段為2.25～4.25 s。

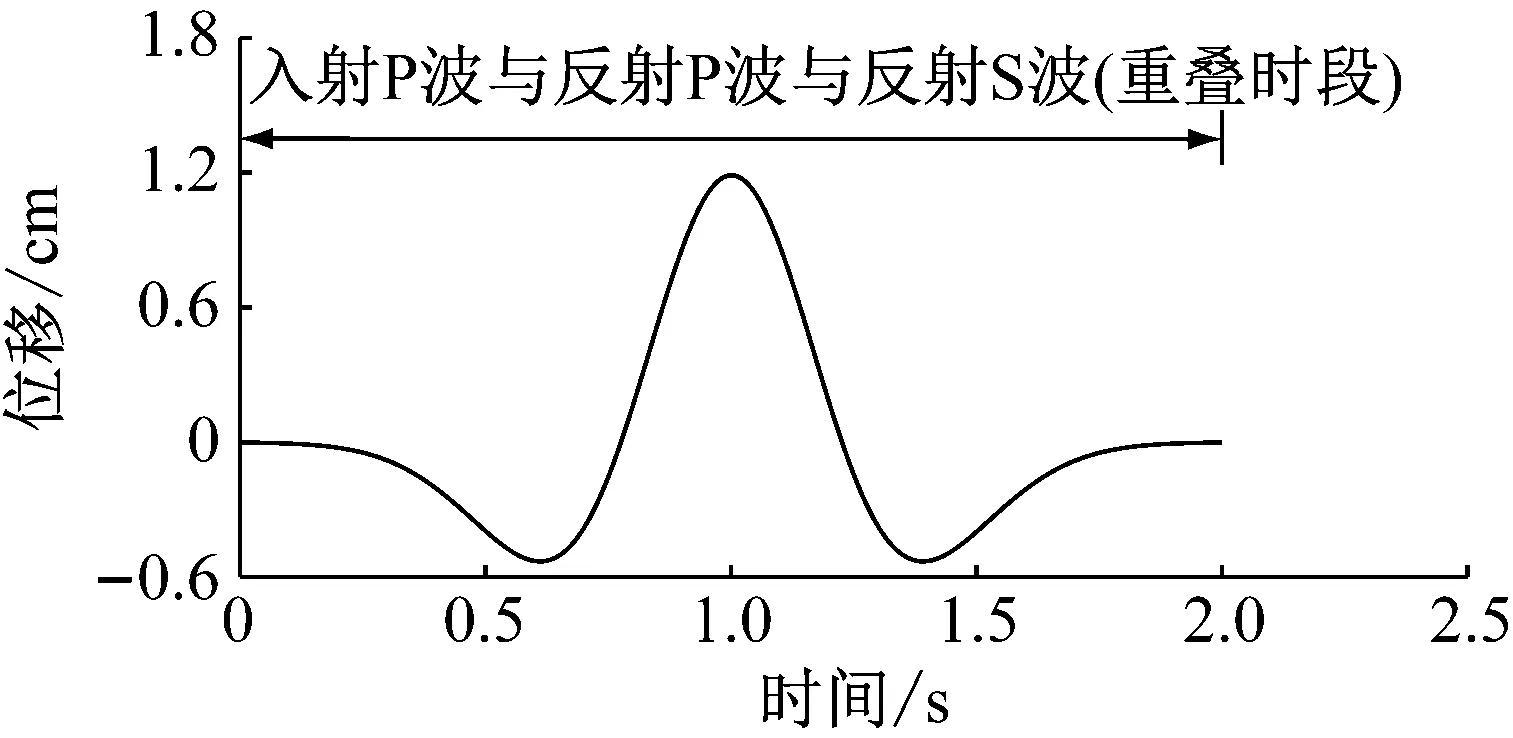
(a) 自由面

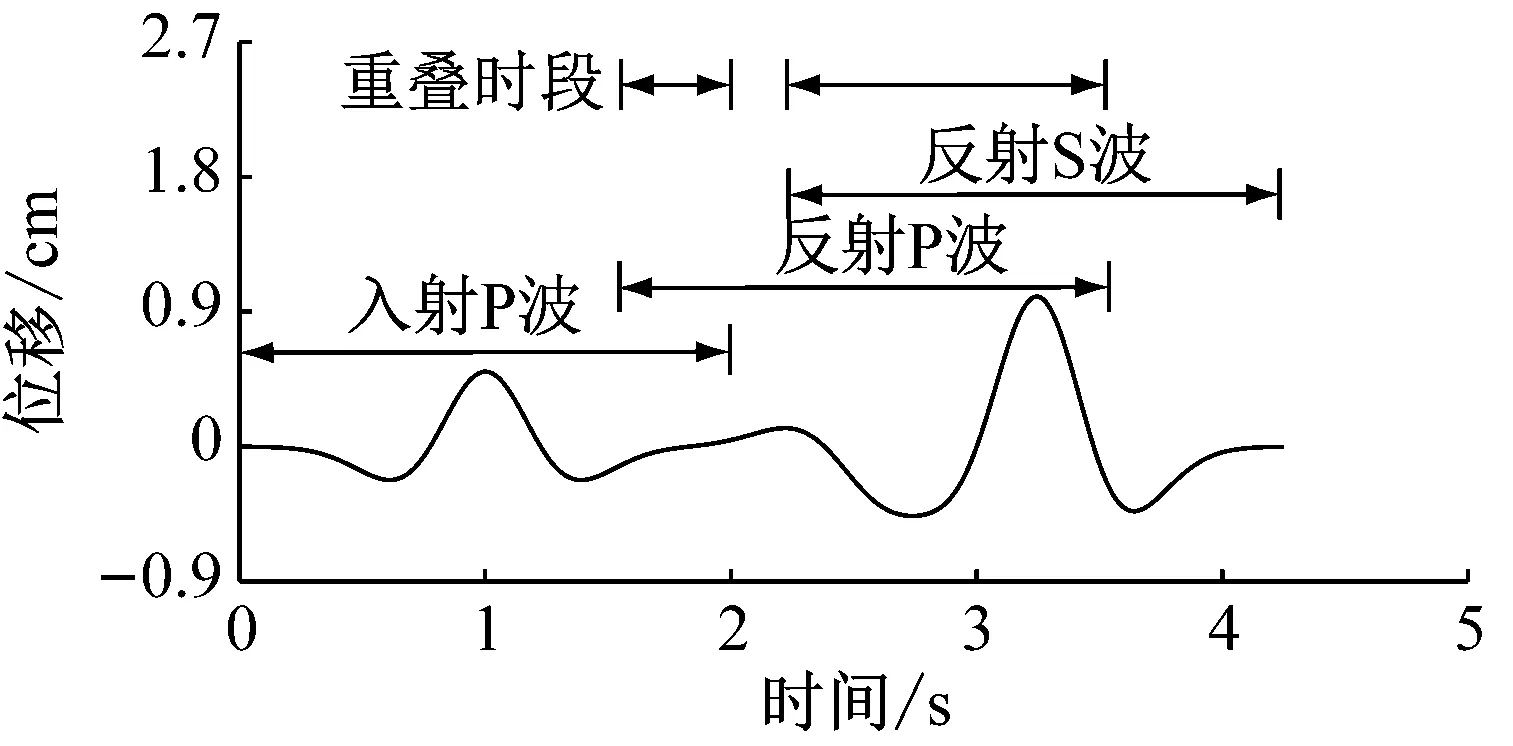
(b) 2 km深度

從質點運動的疊加模式看，質點運動時程可分為單波貢獻時段和多波貢獻時段。對于自由面質點，整個運動時程均為多波貢獻。深度2 km處質點運動時程信息列于表1，在3條地震波影響下，質點運動時程中包含3個單波貢獻時段和2個雙波貢獻時段。

表1 深度2 km質點入射波與反射波貢獻時段

Tab.1 Contribution time of incident and reflect waves on motion of particle at 2 kilometers depth

起止時刻/s貢獻地震波類型0～1.61PI單波貢獻1.61～2.00PI、PR雙波貢獻2.00～2.25PR單波貢獻2.25～2.61PR、SR雙波貢獻3.61～4.25SR單波貢獻

兩個位置質點運動時程對比可看出，受到地震波疊加方式的影響，質點運動不僅出現了持時、峰值的差異，也表現出明顯的時程形狀差異。可見地震波傳播效應所帶來的地震動空間差異顯著且不可忽略。相對于P波垂直入射情況，傾斜入射情況介質內的地震波數量增加，質點運動時程中的地震波貢獻時段劃分更加復雜。

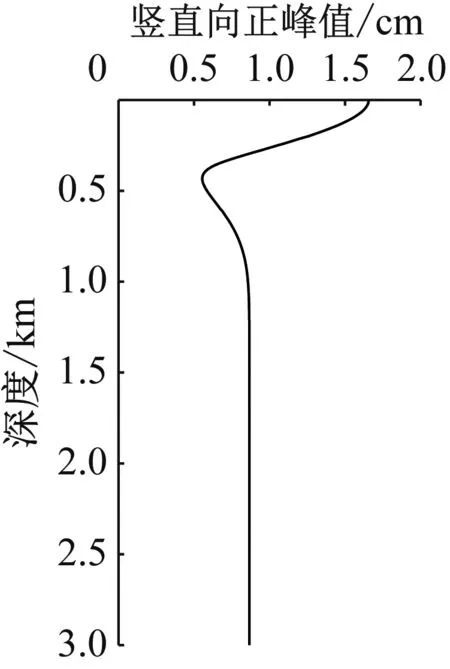
圖9和圖10列出了峰值位移沿豎向的分布。可看出傾斜入射表現規律與垂直入射類似，但由于地震波傾斜入射時半無限介質內地震波數量更多且疊加模式更復雜，與垂直入射規律略有不同。以負峰值為例：由于反射P波與反射S波的分離位置更深，傾斜入射情況幅值變化區域較垂直入射更大；由于反射P波與反射S波幅值與入射波幅值不同，位移峰值沿豎向的變化規律與垂直入射情況存在差異。

5 結 論

本文以波動理論為基礎，針對平面P波入射時半無限介質內質點運動的空間特征開展研究，得出以下結論：

(1) 平面P波垂直入射和傾斜入射兩種情況時，質點運動的空間差異主要沿豎向變化，同高程質點運動僅存在時間滯后，在持時、峰值和時程形狀等方面均保持一致。

(2) 平面P波入射時，依據地震波形成質點運動的疊加模式差異，半無限空間沿深度可劃分為疊加區和分離區。疊加區主要特征為質點運動時程中存在不同地震波的疊加貢獻時段，分離區主要特征為質點運動時程中不同地震波的貢獻時段在時域是分離的。依據波的傳播條件得到平面P波入射時疊加區和分離區的分界線表達式。

(3) 在疊加區域的不同位置，受到地震波間疊加效應的影響，質點運動在持時、峰值和時程形狀方面均可能存在差異。在運動峰值方面，受到入射波和反射波疊加效應影響，接近地面區域均會出現運動峰值隨深度減小逐漸增大的現象。

由于本文選取地震波為簡單的Ricker子波，只能對地震波傳播和疊加模式所產生的質點運動空間差異進行簡單的規律性研究。實際地震引起進入場址的地震波更加復雜，該情況下質點運動的空間特征仍需深入研究。